Mouvement - Vitesse - 2nd L
Classe:
Seconde
I. Mouvement
1. Notion de mouvement

Lorsqu'une voiture démarre, ses roues tournent, sa carrosserie se déplace par rapport à la route et les tous objets fixes sur la terre.
Un corps est en mouvement lorsqu'il change de position dans le temps par rapport à d'autres corps.
2. Relativité du mouvement
Le mouvement et l'immobilité sont des notions toutes relatives.
Un objet $A$ peut être en mouvement par rapport à un objet $B$ mais immobile par rapport à un objet $C.$
Ces observations montrent bien que l'état de mouvement ou de repos d'un corps dépend de l'objet de référence choisi appelé référentiel.
On dit que le mouvement a un caractère relatif : C'est la relativité du mouvement.
II. Référentiels et repères
1. Référentiels
1.1. Définition
Un référentiel est un solide (ou un ensemble de solides) par rapport auquel le mouvement est étudié.
1.2. Exemples de référentiels
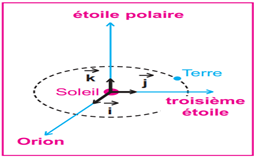
1.2.1. Référentiel héliocentrique
Il a pour origine le centre du système solaire et trois axes dirigés vers trois étoiles fixes.
Il est généralement utilisé des astres ou des planètes du système solaire
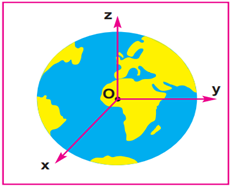
1.2.2. Référentiel géocentrique
Il a pour origine le centre de la Terre et comprend trois axes dirigés vers trois étoiles fixes, parallèles à ceux du référentiel héliocentrique.
Il est généralement utilisé pour l'étude du mouvement d'un satellite de la Terre.
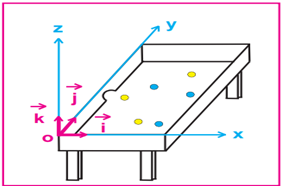
1.2.3. Référentiel terrestre
Le solide de référence est la Terre.
Il est utilisé dans le cadre des études mécaniques effectuées dans un laboratoire ou à partir du sol.
L'objet de référence peut être un arbre, un mur, une table d'expérience... etc
Le référentiel terrestre est encore appelé référentiel de laboratoire
2. Repères d'espace et de temps
Pour décrire le mouvement d'un point mobile, il faut le situer dans l'espace et dans le temps ; d'où la nécessité de choisir un repère d'espace et repère de temps
2.1. Notion de point mobile
Tout objet en mouvement est appelé objet mobile.
Cet objet est considéré comme point mobile si l'étude, sur une distance grande par rapport à ses dimensions porte sur son mouvement global
2.2. Repères d'espaces
Le repère d'espace permet de repérer d'un mobile.
Il est lié au référentiel d'étude
Le choix du repère d'espace se ramène au choix d'un système d'axes liés à la référence
Le repère d'espace peut être :
2.2.1. Le repère cartésien
Dans l'espace tout point $M$ est repéré par ses coordonnées ou ses composantes $x$, $y$ et $z$ ; le vecteur position est :
$$\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}$$
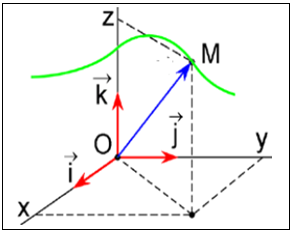
Dans le plan, le point $M$ est repéré par ses coordonnées $x$ et $y$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}+y\vec{j}$$
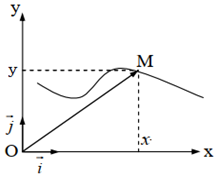
Sur un axe, le point $M$ est repéré par sa coordonnée $x$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}$$

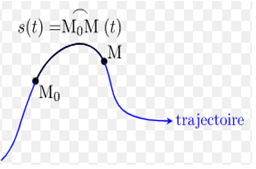
2.2.2. Le repère curviligne
Le mobile est repéré par son abscisse curviligne $S=\overset{\displaystyle\frown}{OM}$
2.2.3. Le repère angulaire
Le repère est constitué par un point origine $O$ associé à une base $\vec{i}$
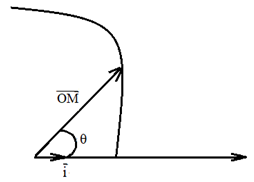
La position du mobile est déterminé par :
$-\ $ la norme $S$ du vecteur :
$-\ $ l'angle polaire
2.3. Repère de temps
$\blacktriangleright\ $ On peut distinguer deux aspects du temps :
$-\ $ l'instant, la date où se produit l'événement.
Chaque instant est caractérisé par un nombre algébrique $t$ appelée date
$-\ $ la durée du phénomène qui mesure l'intervalle de temps entre le début et la fin du phénomène
Deux évènements liant lieu à des dates $t_{i}$ et $t_{f}$ sont séparés par une durée ou intervalle de temps que l'on note :
Dans le système l'unité de temps est la seconde $($symbole : $s)$
$\blacktriangleright\ $ Le repère de temps est l'association :
$-\ $ d'un instant origine ou origine des temps que l'on choisit arbitrairement
$-\ $ d'une unité de temps associé à un compteur de temps : le chronomètre ou l'horloge
3. Trajectoire
Dans un référentiel donné, la trajectoire d'un point mobile est l'ensemble des positions successivement occupées par ce point mobile
Remarque :
$\blacktriangleright\ $ Si la trajectoire est :
$-\ $ une droite, le mouvement est rectiligne ;
$-\ $ un cercle, le mouvement est circulaire ;
$-\ $ une courbe quelconque, le mouvement est curviligne
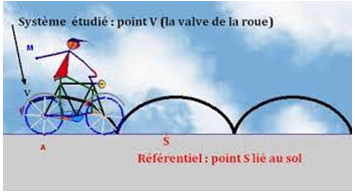
$\blacktriangleright\ $ La trajectoire d'un point mobile est relatif à un référentiel c'est-à-dire, elle dépend du référentiel
Par exemple, la valve d'un vélo en mouvement décrit par rapport au sol, une courbe appelée cycloïde alors que, par rapport à l'axe de la roue, elle décrit un mouvement circulaire
Par rapport à la roue, elle est immobile
III. Vitesse
Dans la vie courante, la distance parcourue et la durée du parcours sont toujours associées
1. Vitesse moyenne
Dans un référentiel donné, la vitesse moyenne d'un point ou d'un objet entre deux instants $t_{i}$ et $t_{f}$ est le rapport de la distance $d$ parcourue par ce point par la durée du parcours $\Delta\,t=t_{f}-t_{i}$ :
$$\begin{array}{l|l} &d=\text{distance parcourue (en m)}\\ \boxed{V_{M}=\dfrac{d}{\Delta\,t}=\dfrac{d}{t_{f}-t_{i}}}&\Delta\,t=t_{f}-t_{i}=\text{durée du parcours (en s)}\\ &V_{M}=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$
$\blacktriangleright\ $ Si la vitesse augmente, le mouvement est accéléré ;
$\blacktriangleright\ $ Si la vitesse diminue, le mouvement est ralenti ou décéléré ou retard
$\blacktriangleright\ $ Si la vitesse est constante, le mouvement est uniforme.
Remarque :
$\blacktriangleright\ $ Il est fréquent d'exprimer une vitesse en kilomètre par heure
$$V(\text{en }m\cdot s^{-1})\stackrel{\times 3.6}{\longrightarrow}V(\text{en }km\cdot h^{-1})$$
$$V(\text{en }m\cdot s^{-1})\stackrel{\div 3.6}{\longleftarrow}V(\text{en }km\cdot h^{-1})$$
$$V(\text{en }m\cdot s^{-1})\stackrel{\div 3.6}{\longleftarrow}V(\text{en }km\cdot h^{-1})$$
$\blacktriangleright\ $ La vitesse moyenne donne une information globale sur le parcours mais ne permet pas de savoir comment il a été : freinage, accélération, arrêt
2. Vitesse instantanée
2.1. Définition
La vitesse instantanée d'un point mobile $M$ est la vitesse à l'instant $t$
Pratiquement cette vitesse instantanée du point mobile, à la date $t$, est égale à sa vitesse moyenne calculée pendant un intervalle très court encadrant l'instant $t$ considérée
$$\begin{array}{l|l} &i\neq 0\\ \boxed{V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}}&t_{i+1}-t_{i-1}=\text{durée du parcours (en s)}\\& V_{i}(t_{i})=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$
2.2. Détermination pratique
Le document ci-dessous est une production de l'enregistrement, à intervalle de temps réguliers $\tau$ du mouvement d'un mobile $M$

Déterminons les expressions des vitesses instantanées $V_{1}\;,\ V_{2}\;,\ V_{3}\ $ et $\ V_{6}$
De manière générale :
$$V_{i}=V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$$
$V_{1}=V_{1}(t_{1})=\dfrac{M_{0}M_{2}}{t_{2}-t_{0}}=\dfrac{M_{0}M_{2}}{2\tau}$ ;
$V_{2}=V_{2}(t_{2})=\dfrac{M_{1}M_{3}}{t_{3}-t_{1}}=\dfrac{M_{1}M_{3}}{2\tau}$ ;
$V_{3}=V_{3}(t_{3})=\dfrac{M_{2}M_{4}}{t_{4}-t_{2}}=\dfrac{M_{2}M_{4}}{2\tau}$ ;
$V_{6}=V_{6}(t_{6})=\dfrac{M_{5}M_{7}}{t_{7}-t_{5}}=\dfrac{M_{5}M_{7}}{2\tau}$
3. Vecteur vitesse instantanée
La valeur de la vitesse instantanée est insuffisante pour caractériser le mouvement d'un point mobile
Elle n'indique pas la direction du mouvement, le sens du mouvement
Pour ces informations, il faut introduire le vecteur vitesse instantanée
3.1. Définition
Le vecteur vitesse instantanée est pratiquement définie par la relation :
$$\overrightarrow{V}_{i}=\overrightarrow{V}_{i}(t_{i})=\dfrac{\overrightarrow{M_{i-1}M_{i+1}}}{t_{i+1}-t_{i-1}}\quad\text{ avec }i\neq 0$$
Exemple :
3.2. Caractéristiques du vecteur vitesse instantanée
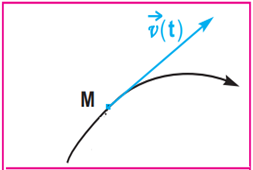
Les caractéristiques du vecteur vitesse instantanée au point $M$ sont
$\surd\ $ le point $M$
$\surd\ $ tangente à la trajectoire au point $M$
$\surd\ $ Sens : celui du mouvement
$\surd\ $ Norme : la valeur $V_{i}=V_{i}(t)=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$
IV. Étude de quelques mouvements
1. Mouvement rectiligne
1.1. Définition
$-\ $ Un mobile est en mouvement rectiligne uniforme s'il se déplace sur une droite avec un vecteur vitesse constant.
Remarque :
Un mobile est en mouvement rectiligne si le mobile parcourt des distances égales pendant des durées égales.

1.2. Loi horaire
Par définition :
$\begin{array}{rcrcl} V=\dfrac{MM_{0}}{t-t_{0}}=\dfrac{x-x_{0}}{t-t_{0}}&\Rightarrow&x-x_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&x&=&V(t-t_{0})+x_{0} \end{array}$
Si $t_{0}=0$ alors, $x=V(t-0)+x_{0}$
Par suite, $x=Vt+x_{0}$
Ainsi, $x$ est une fonction affine du temps
2. Mouvement rectiligne varié
2.1. Définition
$-\ $ Un mobile est en mouvement rectiligne varié s'il se déplace sur une droite avec un vecteur vitesse de module variable.
2.2. Mouvement accéléré et mouvement décéléré
Le mouvement est accéléré si le module du vecteur vitesse croit ; le mouvement est décéléré ou retardé si le module du vecteur vitesse décroit.
Remarque :
$-\ $ Un mobile est en mouvement rectiligne accéléré si le mobile parcourt des distances de plus en plus grandes pendant des durées égales

$-\ $ Un mobile est en mouvement rectiligne décéléré ou retardé si le mobile parcourt des distances de plus en plus petites pendant des durées égales

Le mouvement est uniformément varié si la vitesse est une fonction affine du temps.
3. Mouvement circulaire uniforme
3.1. Définition
$-\ $ Un mobile est en mouvement circulaire uniforme s'il se déplace sur un cercle avec un vecteur vitesse de module constant.
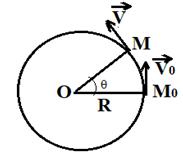
Le vecteur vitesse varie en direction et en sens.
3.2. Loi horaire
Par définition :
$\begin{array}{rcrcl} V=\dfrac{\overset{\displaystyle\frown}{M_{0}M}}{t-t_{0}}=\dfrac{S-S_{0}}{t-t_{0}}&\Rightarrow&S-S_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&S&=&V(t-t_{0})+S_{0}\end{array}$
Par suite, si $t_{0}=0$ alors, $S=Vt+S_{0}$
Il est une relation entre l'abscisse curviligne et l'angle : $S=R\theta$
3.3. La période du mouvement
La durée pour effectuer un tour est appelée période que l'on note $T.$
Le mouvement étant uniforme
$$V=\dfrac{d}{\Delta t}=\dfrac{2\pi R}{T}\Rightarrow T=\dfrac{2\pi R}{V}$$
$T$ est constant, car $R$ est fixe et $V$ est constant
3.3. La fréquence du mouvement
La fréquence du mouvement représente le nombre de périodes par seconde
$$N=\dfrac{1}{T}\quad\text{ ou }\quad N=\dfrac{V}{2\pi R}$$
La fréquence $N$ s'exprime en hertz $($symbole : $Hz)$
V. Mouvement de translation et de rotation d'un solide
1. Mouvement de translation d'un solide
1.1. Définition
Un solide (ou objet indéformable) effectue un mouvement de translation lorsque n'importe quel segment de ce solide se déplace en conservant sa direction.
1.2. Les différents types de translation
La translation peut être :
$-\ $ rectiligne : chaque point du solide décrit une droite
$-\ $ curviligne : chaque du solide décrit une courbe
$-\ $ circulaire : chaque du solide décrit un cercle
2. Mouvement de rotation d'un solide
2.1. Définition
Un solide est un mouvement de rotation si les points d'un mobile en rotation décrivent des cercles ou des arcs de cercle centrés sur la même droite, appelée axe de rotation.
Cet axe est perpendiculaire aux plans du cercle.
2.2. Vitesse angulaire
La vitesse angulaire est l'angle balayé par seconde
$$\begin{array}{l|l} &\alpha\text{ angle radians (rad)}\\\boxed{\omega=\dfrac{\alpha}{\Delta t}}&\Delta t=t_{f}-t_{i}=\text{durée en seconde (s)}\\&\omega=\text{vitesse angulaire en radians par seconde }(rad\cdot s^{-1}) \end{array}$$
2.3. Relation entre vitesse d'un point et vitesse angulaire
Par définition :
$v=\dfrac{S}{\Delta t}=\dfrac{R\alpha}{\Delta t}=R\dfrac{\alpha}{\Delta t}$
Or, $\omega=\dfrac{\alpha}{\Delta t}$ donc, $v=R\omega$
I. Mouvement
1. Notion de mouvement

Lorsqu'une voiture démarre, ses roues tournent, sa carrosserie se déplace par rapport à la route et les tous objets fixes sur la terre.
Un corps est en mouvement lorsqu'il change de position dans le temps par rapport à d'autres corps.
2. Relativité du mouvement
Le mouvement et l'immobilité sont des notions toutes relatives.
Un objet $A$ peut être en mouvement par rapport à un objet $B$ mais immobile par rapport à un objet $C.$
Ces observations montrent bien que l'état de mouvement ou de repos d'un corps dépend de l'objet de référence choisi appelé référentiel.
On dit que le mouvement a un caractère relatif : C'est la relativité du mouvement.
II. Référentiels et repères
1. Référentiels
1.1. Définition
Un référentiel est un solide (ou un ensemble de solides) par rapport auquel le mouvement est étudié.
1.2. Exemples de référentiels
1.2.1. Référentiel héliocentrique
Il a pour origine le centre du système solaire et trois axes dirigés vers trois étoiles fixes.
Il est généralement utilisé des astres ou des planètes du système solaire

1.2.2. Référentiel géocentrique
Il a pour origine le centre de la Terre et comprend trois axes dirigés vers trois étoiles fixes, parallèles à ceux du référentiel héliocentrique.
Il est généralement utilisé pour l'étude du mouvement d'un satellite de la Terre.

1.2.3. Référentiel terrestre
Le solide de référence est la Terre.
Il est utilisé dans le cadre des études mécaniques effectuées dans un laboratoire ou à partir du sol.
L'objet de référence peut être un arbre, un mur, une table d'expérience... etc
Le référentiel terrestre est encore appelé référentiel de laboratoire

2. Repères d'espace et de temps
Pour décrire le mouvement d'un point mobile, il faut le situer dans l'espace et dans le temps ; d'où la nécessité de choisir un repère d'espace et repère de temps
2.1. Notion de point mobile
Tout objet en mouvement est appelé objet mobile.
Cet objet est considéré comme point mobile si l'étude, sur une distance grande par rapport à ses dimensions porte sur son mouvement global
2.2. Repères d'espaces
Le repère d'espace permet de repérer d'un mobile.
Il est lié au référentiel d'étude
Le choix du repère d'espace se ramène au choix d'un système d'axes liés à la référence
Le repère d'espace peut être :
2.2.1. Le repère cartésien
Dans l'espace tout point $M$ est repéré par ses coordonnées ou ses composantes $x$, $y$ et $z$ ; le vecteur position est :
$$\overrightarrow{OM}=x\vec{i}+y\vec{j}+z\vec{k}$$

Dans le plan, le point $M$ est repéré par ses coordonnées $x$ et $y$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}+y\vec{j}$$

Sur un axe, le point $M$ est repéré par sa coordonnée $x$, le vecteur position est :$$\overrightarrow{OM}=x\vec{i}$$

2.2.2. Le repère curviligne
Le mobile est repéré par son abscisse curviligne $S=\overset{\displaystyle\frown}{OM}$

2.2.3. Le repère angulaire
Le repère est constitué par un point origine $O$ associé à une base $\vec{i}$

La position du mobile est déterminé par :
$-\ $ la norme $S$ du vecteur :
$-\ $ l'angle polaire
2.3. Repère de temps
$\blacktriangleright\ $ On peut distinguer deux aspects du temps :
$-\ $ l'instant, la date où se produit l'événement.
Chaque instant est caractérisé par un nombre algébrique $t$ appelée date
$-\ $ la durée du phénomène qui mesure l'intervalle de temps entre le début et la fin du phénomène
Deux évènements liant lieu à des dates $t_{i}$ et $t_{f}$ sont séparés par une durée ou intervalle de temps que l'on note :
Dans le système l'unité de temps est la seconde $($symbole : $s)$
$\blacktriangleright\ $ Le repère de temps est l'association :
$-\ $ d'un instant origine ou origine des temps que l'on choisit arbitrairement
$-\ $ d'une unité de temps associé à un compteur de temps : le chronomètre ou l'horloge
3. Trajectoire
Dans un référentiel donné, la trajectoire d'un point mobile est l'ensemble des positions successivement occupées par ce point mobile
Remarque :
$\blacktriangleright\ $ Si la trajectoire est :
$-\ $ une droite, le mouvement est rectiligne ;
$-\ $ un cercle, le mouvement est circulaire ;
$-\ $ une courbe quelconque, le mouvement est curviligne
$\blacktriangleright\ $ La trajectoire d'un point mobile est relatif à un référentiel c'est-à-dire, elle dépend du référentiel
Par exemple, la valve d'un vélo en mouvement décrit par rapport au sol, une courbe appelée cycloïde alors que, par rapport à l'axe de la roue, elle décrit un mouvement circulaire
Par rapport à la roue, elle est immobile

III. Vitesse
Dans la vie courante, la distance parcourue et la durée du parcours sont toujours associées
1. Vitesse moyenne
Dans un référentiel donné, la vitesse moyenne d'un point ou d'un objet entre deux instants $t_{i}$ et $t_{f}$ est le rapport de la distance $d$ parcourue par ce point par la durée du parcours $\Delta\,t=t_{f}-t_{i}$ :
$$\begin{array}{l|l} &d=\text{distance parcourue (en m)}\\ \boxed{V_{M}=\dfrac{d}{\Delta\,t}=\dfrac{d}{t_{f}-t_{i}}}&\Delta\,t=t_{f}-t_{i}=\text{durée du parcours (en s)}\\ &V_{M}=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$
$\blacktriangleright\ $ Si la vitesse augmente, le mouvement est accéléré ;
$\blacktriangleright\ $ Si la vitesse diminue, le mouvement est ralenti ou décéléré ou retard
$\blacktriangleright\ $ Si la vitesse est constante, le mouvement est uniforme.
Remarque :
$\blacktriangleright\ $ Il est fréquent d'exprimer une vitesse en kilomètre par heure
$$V(\text{en }m\cdot s^{-1})\stackrel{\times 3.6}{\longrightarrow}V(\text{en }km\cdot h^{-1})$$
$$V(\text{en }m\cdot s^{-1})\stackrel{\div 3.6}{\longleftarrow}V(\text{en }km\cdot h^{-1})$$
$$V(\text{en }m\cdot s^{-1})\stackrel{\div 3.6}{\longleftarrow}V(\text{en }km\cdot h^{-1})$$
$\blacktriangleright\ $ La vitesse moyenne donne une information globale sur le parcours mais ne permet pas de savoir comment il a été : freinage, accélération, arrêt
2. Vitesse instantanée
2.1. Définition
La vitesse instantanée d'un point mobile $M$ est la vitesse à l'instant $t$
Pratiquement cette vitesse instantanée du point mobile, à la date $t$, est égale à sa vitesse moyenne calculée pendant un intervalle très court encadrant l'instant $t$ considérée
$$\begin{array}{l|l} &i\neq 0\\ \boxed{V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}}&t_{i+1}-t_{i-1}=\text{durée du parcours (en s)}\\& V_{i}(t_{i})=\text{vitesse en mètres par seconde (en m/s)} \end{array}$$
2.2. Détermination pratique
Le document ci-dessous est une production de l'enregistrement, à intervalle de temps réguliers $\tau$ du mouvement d'un mobile $M$

Déterminons les expressions des vitesses instantanées $V_{1}\;,\ V_{2}\;,\ V_{3}\ $ et $\ V_{6}$
De manière générale :
$$V_{i}=V_{i}(t_{i})=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$$
$V_{1}=V_{1}(t_{1})=\dfrac{M_{0}M_{2}}{t_{2}-t_{0}}=\dfrac{M_{0}M_{2}}{2\tau}$ ;
$V_{2}=V_{2}(t_{2})=\dfrac{M_{1}M_{3}}{t_{3}-t_{1}}=\dfrac{M_{1}M_{3}}{2\tau}$ ;
$V_{3}=V_{3}(t_{3})=\dfrac{M_{2}M_{4}}{t_{4}-t_{2}}=\dfrac{M_{2}M_{4}}{2\tau}$ ;
$V_{6}=V_{6}(t_{6})=\dfrac{M_{5}M_{7}}{t_{7}-t_{5}}=\dfrac{M_{5}M_{7}}{2\tau}$
3. Vecteur vitesse instantanée
La valeur de la vitesse instantanée est insuffisante pour caractériser le mouvement d'un point mobile
Elle n'indique pas la direction du mouvement, le sens du mouvement
Pour ces informations, il faut introduire le vecteur vitesse instantanée
3.1. Définition
Le vecteur vitesse instantanée est pratiquement définie par la relation :
$$\overrightarrow{V}_{i}=\overrightarrow{V}_{i}(t_{i})=\dfrac{\overrightarrow{M_{i-1}M_{i+1}}}{t_{i+1}-t_{i-1}}\quad\text{ avec }i\neq 0$$
Exemple :
3.2. Caractéristiques du vecteur vitesse instantanée
Les caractéristiques du vecteur vitesse instantanée au point $M$ sont
$\surd\ $ le point $M$
$\surd\ $ tangente à la trajectoire au point $M$
$\surd\ $ Sens : celui du mouvement
$\surd\ $ Norme : la valeur $V_{i}=V_{i}(t)=\dfrac{M_{i-1}M_{i+1}}{t_{i+1}-t_{i-1}}=\dfrac{M_{i-1}M_{i+1}}{2\tau}$

IV. Étude de quelques mouvements
1. Mouvement rectiligne
1.1. Définition
$-\ $ Un mobile est en mouvement rectiligne uniforme s'il se déplace sur une droite avec un vecteur vitesse constant.
Remarque :
Un mobile est en mouvement rectiligne si le mobile parcourt des distances égales pendant des durées égales.

1.2. Loi horaire
Par définition :
$\begin{array}{rcrcl} V=\dfrac{MM_{0}}{t-t_{0}}=\dfrac{x-x_{0}}{t-t_{0}}&\Rightarrow&x-x_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&x&=&V(t-t_{0})+x_{0} \end{array}$
Si $t_{0}=0$ alors, $x=V(t-0)+x_{0}$
Par suite, $x=Vt+x_{0}$
Ainsi, $x$ est une fonction affine du temps
2. Mouvement rectiligne varié
2.1. Définition
$-\ $ Un mobile est en mouvement rectiligne varié s'il se déplace sur une droite avec un vecteur vitesse de module variable.
2.2. Mouvement accéléré et mouvement décéléré
Le mouvement est accéléré si le module du vecteur vitesse croit ; le mouvement est décéléré ou retardé si le module du vecteur vitesse décroit.
Remarque :
$-\ $ Un mobile est en mouvement rectiligne accéléré si le mobile parcourt des distances de plus en plus grandes pendant des durées égales

$-\ $ Un mobile est en mouvement rectiligne décéléré ou retardé si le mobile parcourt des distances de plus en plus petites pendant des durées égales

Le mouvement est uniformément varié si la vitesse est une fonction affine du temps.
3. Mouvement circulaire uniforme
3.1. Définition
$-\ $ Un mobile est en mouvement circulaire uniforme s'il se déplace sur un cercle avec un vecteur vitesse de module constant.

Le vecteur vitesse varie en direction et en sens.
3.2. Loi horaire
Par définition :
$\begin{array}{rcrcl} V=\dfrac{\overset{\displaystyle\frown}{M_{0}M}}{t-t_{0}}=\dfrac{S-S_{0}}{t-t_{0}}&\Rightarrow&S-S_{0}&=&V(t-t_{0})\\ \\&\Rightarrow&S&=&V(t-t_{0})+S_{0}\end{array}$
Par suite, si $t_{0}=0$ alors, $S=Vt+S_{0}$
Il est une relation entre l'abscisse curviligne et l'angle : $S=R\theta$
3.3. La période du mouvement
La durée pour effectuer un tour est appelée période que l'on note $T.$
Le mouvement étant uniforme
$$V=\dfrac{d}{\Delta t}=\dfrac{2\pi R}{T}\Rightarrow T=\dfrac{2\pi R}{V}$$
$T$ est constant, car $R$ est fixe et $V$ est constant
3.3. La fréquence du mouvement
La fréquence du mouvement représente le nombre de périodes par seconde
$$N=\dfrac{1}{T}\quad\text{ ou }\quad N=\dfrac{V}{2\pi R}$$
La fréquence $N$ s'exprime en hertz $($symbole : $Hz)$
V. Mouvement de translation et de rotation d'un solide
1. Mouvement de translation d'un solide
1.1. Définition
Un solide (ou objet indéformable) effectue un mouvement de translation lorsque n'importe quel segment de ce solide se déplace en conservant sa direction.
1.2. Les différents types de translation
La translation peut être :
$-\ $ rectiligne : chaque point du solide décrit une droite
$-\ $ curviligne : chaque du solide décrit une courbe
$-\ $ circulaire : chaque du solide décrit un cercle
2. Mouvement de rotation d'un solide
2.1. Définition
Un solide est un mouvement de rotation si les points d'un mobile en rotation décrivent des cercles ou des arcs de cercle centrés sur la même droite, appelée axe de rotation.
Cet axe est perpendiculaire aux plans du cercle.
2.2. Vitesse angulaire
La vitesse angulaire est l'angle balayé par seconde
$$\begin{array}{l|l} &\alpha\text{ angle radians (rad)}\\\boxed{\omega=\dfrac{\alpha}{\Delta t}}&\Delta t=t_{f}-t_{i}=\text{durée en seconde (s)}\\&\omega=\text{vitesse angulaire en radians par seconde }(rad\cdot s^{-1}) \end{array}$$
2.3. Relation entre vitesse d'un point et vitesse angulaire
Par définition :
$v=\dfrac{S}{\Delta t}=\dfrac{R\alpha}{\Delta t}=R\dfrac{\alpha}{\Delta t}$
Or, $\omega=\dfrac{\alpha}{\Delta t}$ donc, $v=R\omega$

Commentaires
Aminata (non vérifié)
sam, 05/03/2025 - 00:38
Permalien
La réussite
Ajouter un commentaire