Réaction nucléaire - Ts
Classe:
Terminale
I. Le noyau atomique
I.1. Définitions
Le noyau atomique est la partie centrale de l'atome constituée de nucléons (protons + neutrons).
Un noyau d'un élément $X$ est représenté symboliquement par : $$_{Z}^{A}X$$
$-\ \ X$ représente le symbole chimique de l'élément
$-\ \ A$ est appelé nombre de masse ou nombre de nucléons (protons + neutrons)
$-\ \ Z$ est le nombre de charge ou numéro atomique ou encore nombre de protons
Un élément chimique est l'ensemble des atomes de même nombre de charge $Z.$
Des noyaux comportant le même nombre de protons mais un nombre différent de neutrons, sont appelés isotopes.
Remarque
$N=A-Z$ représente le nombre de neutrons
I.2. Équivalence masse - énergie : relation d'Einstein
Tout système de masse $m$ possède une énergie $E$ appelée énergie de masse telle que : $$\boxed{E=m.c^{2}}$$
où $E$ en $(J)\;,\ m$ en $kg\ $ et $\ c=3\;10^{8}\;m.s^{-1}$ (vitesse de la lumière dans le vide).
Remarque
A l'échelle atomique on utilise l'électronvolt $(eV)$, une unité mieux adaptée que le Joule. On a : $$1\;eV=1.6\;10^{-19}\;J\;,\quad 1\;MeV=1.6\;10^{-13}\;J$$
I.3. Énergie de liaison ou de cohésion d'un noyau
I.3.1. Défaut de masse
La masse d'un noyau est toujours inférieure à la somme des masses des nucléons qui le composent, pris au repos.
Pour le nucléide $_{Z}^{A}X$, le défaut de masse $\Delta m$ est donné par : $$\boxed{\Delta m=Zm_{\text{proton}}+(A-Z)m_{\text{neutron}}-m\left(_{Z}^{A}X\right)}$$
I.3.2. Unité de masse atomique (u)
Comme pour l'énergie, on peut utiliser une autre unité que le kilogramme ; c'est l'unité de masse atomique (u). Elle correspond au $12^{e}$ de la masse d'un atome de carbone 12 : $$1\;\text{u}=1.66\;10^{-27}\;kg$$
En effet,
$\begin{array}{rcl} 1\;\text{u}&=&\dfrac{1}{12}m_{a}(C)\quad\text{avec }m_{a}(C)=\dfrac{M_{C}}{\mathcal{N}_{A}}\\ \\&=&\dfrac{1}{12}\times\dfrac{M_{C}}{\mathcal{N}_{A}}\quad\text{avec }\mathcal{N}_{A}\;\text{ le nombre d'Avogadro}\end{array}$
A.N : $1\;\text{u}=\dfrac{1}{12}\times\dfrac{12\;10^{-3}}{6.02\;10^{23}}=1.66\;10^{-27}$
D'où : $1\;\text{u}=1.66\;10^{-27}\;kg$
I.3.3. Définition
L'énergie de liaison $E_{\ell}$ d'un noyau est l'énergie qu'il faut fournir à ce noyau au repos, pour obtenir tous ses nucléons dissociés et au repos.
$$\boxed{E_{\ell}=\Delta m.c^{2}}$$
Remarque
Pour une unité de masse atomique $(1\;\text{u})$, l'énergie de liaison est donnée par : $$E_{\ell}=1\;\text{u}\times c^{2}=931.5\;MeV$$
I.3.4. Énergie de liaison par nucléon
L'énergie de liaison augmente avec le nombre de nucléon. Donc, pour pouvoir comparer la stabilité des noyaux, on définit l'énergie de liaison par nucléon $E_{A}$ par : $$\boxed{E_{A}=\dfrac{E_{\ell}}{A}\ \text{ en }\;MeV/\text{nucléon}}$$
Remarque
Un noyau est stable si $E_{A}>8\;MeV/\text{nucléon}.$
II. La radioactivité
II.1. Définition
Un noyau instable est dit radioactif et se désintégrera.
La radioactivité naturelle est ce phénomène de transformations (désintégration), aléatoires et spontanées des nucléides instables.
Les nucléides instables sont aussi appelés radio-éléments ou radio-nucléides.
Soit l'équation de désintégration suivante :
$$_{Z}^{A}X\ \longrightarrow\ _{Z_{1}}^{A_{1}}Y+_{Z_{2}}^{A_{2}}T$$
où $T\ $ et $\ Y$ sont les noyaux fils.
$-\ \ $ pour déterminer $A_{1}\ $ et $\ A_{2}$, on utilise la loi de conservation du nombre de nucléons. $$A=A_{1}+A_{2}$$
$-\ \ $ pour déterminer $Z_{1}\ $ et $\ Z_{2}$, on utilise la loi de conservation de la charge. $$Z=Z_{1}+Z_{2}$$
II.2. Les différents types de radioactivité
II.2.1 Radioactivité $\alpha$
Un noyau est dit radioactif $\alpha$ lorsqu'il se désintègre en émettant une particule positive $\alpha$, qui est un noyau d'hélium $_{2}^{4}He.$
La radioactivité $\alpha$ caractérise des noyaux lourds $(A>200).$
Équation bilan de la désintégration : $$\boxed{_{Z}^{A}X\ \longrightarrow\ _{(Z-2)}^{(A-4)}Y+_{2}^{4}He}$$
Exemple : $_{\ 90}^{227}Th\ \longrightarrow\ _{\ 88}^{223}Ra+_{2}^{4}He$
II.2.2. Radioactivité $\beta^{-}$
Un noyau est dit radioactif $\beta^{-}$ lorsqu'il se désintègre en émettant un électron $_{-1}^{\;\ 0}e.$
La radioactivité $\beta^{-}$ caractérise des noyaux riches en neutrons et lors de la désintégration un neutron du noyau se transforme en un proton et un électron selon l'équation bilan suivante : $_{0}^{1}n\ \longrightarrow\ _{1}^{1}p+_{-1}^{\;\ 0}e$
Équation bilan de la désintégration : $$\boxed{_{Z}^{A}X\ \longrightarrow\ _{(Z+1)}^{\quad A}Y+_{-1}^{\;\ 0}e}$$
Exemple : $_{\ 55}^{137}Cs\ \longrightarrow\ _{\ 56}^{137}Ba+_{-1}^{\;\ 0}e$
II.2.3. Radioactivité $\beta^{+}$
Un noyau est radioactif $\beta^{+}$ lorsqu'il se désintègre en émettant un positon $_{+1}^{\;\ 0}e.$
La radioactivité $\beta^{+}$ caractérise des noyaux riches en protons et lors de la désintégration un proton du noyau se transforme en un positon et un neutron selon l'équation bilan suivante : $_{1}^{1}p\ \longrightarrow\ _{0}^{1}n+_{+1}^{\;\ 0}e$
Équation bilan de la désintégration : $$\boxed{_{Z}^{A}X\ \longrightarrow\ _{(Z-1)}^{\quad A}Y+_{+1}^{\;\ 0}e}$$
Exemple : $_{15}^{30}P\ \longrightarrow\ _{14}^{30}Si+_{+1}^{\;\ 0}e$
II.2.4. Le rayonnement $\gamma$
Lors de chaque désintégration $\alpha\;,\ \beta^{-}\;,\ \beta^{+}$, le noyau fils émis est, le plus souvent, à l'état excité. Il a donc tendance à retourner à son état fondamental, par désexcitation, en libérant le surplus d'énergie sous forme de rayonnements $\gamma$ selon l'équation : $_{Z}^{A}Y^{*}\ \longrightarrow\ _{Z}^{A}Y+\gamma$
où, $Y^{*}$ est le noyau fils instable ou excité et la particule $\gamma$ est un photon.
Exemple : $_{\ 55}^{135}Cs^{*}\ \longrightarrow\ _{\ 55}^{135}Cs+\gamma$
Remarque
Le rayonnement $\gamma$ est très pénétrant et peut donc traverser plusieurs mètres de béton.
III. Loi de décroissance radioactive
III.1. Loi de décroissance
Si $N_{0}$ est le nombre initial de noyaux (à l'instant $t=0$) et $N$ le nombre de noyaux restant à l'instant $t$, après désintégration alors, sur un intervalle de temps très court $\mathrm{d}t$ la variation du nombre de noyaux est donnée par : $$\dfrac{\mathrm{d}N}{\mathrm{d}t}=-\lambda N$$
où $\lambda$ est la constante radioactive exprimée en $s^{-1}.$
Cette équation différentielle, de la forme $N'+\lambda N=0$ a pour solution $N(t)=k\mathrm{e}^{-\lambda t}.$
Or, à $t=0\;,\ N=N_{0}$ donc, $k=N_{0}.$
D'où, la relation suivante, caractéristique de la loi de décroissance radioactive : $$\boxed{N(t)=N_{0}\mathrm{e}^{-\lambda t}}$$
Remarque
$-\ \ $ On définit la constante de temps $\tau$ comme étant égale à $\dfrac{1}{\lambda}.$
$-\ \ $ Si $m$ est la masse des $N$ noyaux non désintégrés et $m_{0}$ la masse des $N_{0}$ noyaux initiaux alors, $m=m_{0}\mathrm{e}^{-\lambda t}.$
III.2. Période radioactive - Demi-vie
La période radioactive $T$ ou demi-vie $t_{1/2}$ correspond au temps nécessaire pour que la moitié des noyaux initiaux se soit désintégrée et on a : $$\boxed{T=\dfrac{\ln 2}{\lambda}=\tau\ln 2}$$
En effet, à $t=T$ on a $N=\dfrac{N_{0}}{2}$
Or, $N(t)=N_{0}\mathrm{e}^{-\lambda t}$ donc,
$\begin{array}{rcrcl} \dfrac{N_{0}}{2}=N_{0}\mathrm{e}^{-\lambda T}&\Rightarrow&\dfrac{1}{2}&=&\mathrm{e}^{-\lambda T}\\ \\&\Rightarrow&-\ln 2&=&-\lambda T\\ \\&\Rightarrow&T&=&\dfrac{\ln 2}{\lambda}\end{array}$
D'où, $T=\dfrac{\ln 2}{\lambda}$
Remarque : à $t=nT\;,\ N=\dfrac{N_{0}}{2^{n}}$
$\centerdot\ \ $ Détermination graphique des constantes $T\;,\ \tau\ $ et $\ \lambda$
Considérons la représentation graphique ci-dessous de $N(t)=N_{0}\mathrm{e}^{-\lambda t}$
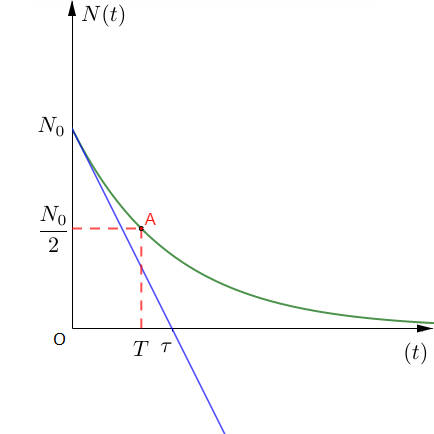
La période $T$ ou demi-vie est obtenue en projetant la valeur $\dfrac{N_{0}}{2}$ sur la courbe. C'est donc l'abscisse du point $A$ d'ordonnée $\dfrac{N_{0}}{2}.$
Pour déterminer $\tau$ on trace la tangente à la courbe à $t=0$ qui coupe l'axe des abscisses pour $t=\tau.$
Pour la détermination graphique de $\lambda$, on peut considérer la courbe représentative ci-dessous de la fonction $\ln N(t)=-\lambda t+\ln N_{0}.$
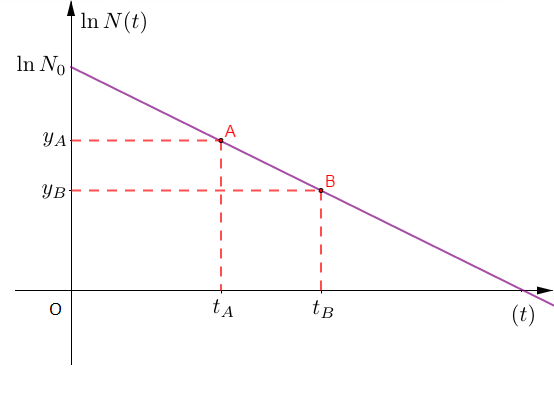
On constate que c'est une droite affine de coefficient directeur $-\lambda.$
Donc, en choisissant deux points $A$ et $B$ de cette droite, on aura : $$-\lambda=\dfrac{y_{B}-y_{A}}{t_{B}-t_{A}}$$
Remarque
On peut aussi, pour la détermination graphique de $\lambda$, considérer la fonction $-\ln\left(\dfrac{N}{N_{0}}\right)=\lambda t.$ Donc, $\lambda$ est coefficient directeur de la droite linéaire représentant cette fonction.
III.3. Activité radioactive $\mathcal{A}$
L'activité $\mathcal{A}$ d'une source radioactive est définie comme étant égale au nombre de désintégrations par seconde : c'est la vitesse de désintégration. On a : $$\mathcal{A}=-\dfrac{\mathrm{d}N}{\mathrm{d}t}$$
Comme $N(t)=N_{0}\mathrm{e}^{-\lambda t}$ alors, $-\mathrm{d}N=\lambda N\mathrm{d}t$
Donc, $\mathcal{A}=\lambda N=\lambda N_{0}\mathrm{e}^{-\lambda t}$
D'où, la loi de décroissance de l'activité $\mathcal{A}$ est donnée par : $$\boxed{\mathcal{A}=\mathcal{A}_{0}\mathrm{e}^{-\lambda t}}$$
où $\mathcal{A}_{0}=\lambda N_{0}$ est le nombre de désintégration par seconde à l'instant initial.
L'unité de $\mathcal{A}$ est le Becquerel $(Bq).$
1 Bq correspond à une désintégration/seconde
Exercice d'application
Le césium $_{\ 55}^{137}Cs$ se désintègre en donnant du baryum $Ba$ et en émettant une particule $\beta^{-}.$ La période radioactive $T$ est de $30$ ans.
Un échantillon a été préparé en mars $1952$, son activité était alors de $3\;10^{4}\;Bq.$
1) Écrire l'équation de la désintégration
2) Donner l'activité de la source en mars $1997.$
Résolution
1) On sait que l'équation générale de la radioactivité $\beta^{-}$ est donnée par : $$_{Z}^{A}X\ \longrightarrow\ _{(Z+1)}^{\quad A}Y+_{-1}^{\;\ 0}e$$
D'où, pour le césium $_{\ 55}^{137}Cs$ on obtient :
$$_{\ 55}^{137}Cs\ \longrightarrow\ _{\ 56}^{137}Ba+_{-1}^{\;\ 0}e$$
2) A l'instant $t=t=_{1}$ on a : $\mathcal{A}=\mathcal{A}_{0}\mathrm{e}^{-\lambda t_{1}}$
Or, $t_{1}=45\text{ ans}$ (de mars $1952$ à mars $1997$), $\lambda=\dfrac{\ln 2}{T}$ et $\mathcal{A}_{0}$ correspondant à l'activité de la source en mars $1952.$
Donc, $\mathcal{A}=\mathcal{A}_{0}\mathrm{e}^{-\tfrac{t_{1}\ln 2}{T}}$
A.N : $\mathcal{A}=3\;10^{4}\mathrm{e}^{-\tfrac{45\ln 2}{30}}=10.6\;10^{3}$
D'où : $\boxed{\mathcal{A}=10.6\;10^{3}\;Bq}$
IV. Réactions nucléaires provoquées
Parmi les noyaux instables ou radioactifs on distingue : des noyaux légers $(A<20)$ qui vont pouvoir fusionner et des noyaux lourds $(A>190)$ qui ont tendance à subir des réaction de fission, en libérant beaucoup d'énergie.
IV.1. Réaction de fission
C'est une réaction nucléaire provoquée par l'impact d'un neutron sur un noyau lourd qui, après le choc, se scinde en deux noyaux légers.
Le choix du noyau lourd subissant la fission dépend de son énergie de liaison et de son abondance.
Par ailleurs, la réaction libère d'autres neutrons qui peuvent entrer en collision avec d'autres noyaux lourds. Ce qui pourra donc provoquer de nouvelles réactions de fission.
Ainsi, la fission est une réaction en chaine.
Exemple : $_{\ 92}^{235}U+_{0}^{1}n\ \longrightarrow\ _{38}^{94}Sr+_{\ 54}^{140}Xe+2_{0}^{1}n$
IV.2. Réaction de fusion
C'est une réaction nucléaire au cours de laquelle deux noyaux légers vont se lier pour donner un noyau plus lourd, sous une température très élevée $(>10^{8}\;K).$
Exemple : $_{2}^{3}He+_{2}^{3}He\ \longrightarrow\ _{2}^{4}He+2_{1}^{1}p$
Remarques
Pour ces deux réactions :
$-\ \ $ L'énergie de liaison par nucléon des noyaux subissant la réaction est inférieure à celles des noyaux obtenus.
$-\ \ $ Les lois de conservation de la charge et du nombre de nucléons sont encore vérifiées.
V. Énergie libérée
L'énergie libérée, $E_{\text{libérée}}$, lors d'une réaction nucléaire, est donnée par : $$\boxed{E_{\text{libérée}}=|m_{\text{produits}}-m_{\text{réactifs}}|\times c^{2}}$$
Cette énergie est transformée, d'une part en rayonnement, d'autre part en énergie cinétique utilisée par les noyaux fils et les particules émises.
Exercice d'application
La fission d'un noyau d'uranium $235$ est représentée par l'équation suivante : $$_{\ 92}^{235}U+_{0}^{1}n\ \longrightarrow\ _{40}^{93}Zr+_{\ 52}^{140}Te+2_{0}^{1}n$$
1) Calculer l'énergie de liaison de l'uranium.
2) Calculer l'énergie libérée au cours de la fission d'un atome d'uranium $235.$
Les énergies de liaison par nucléon sont données en $MeV/\text{nucléon}$ par : $$^{235}U\;:\;7.5\;;\quad ^{93}Zr\;:\;8.6\;;\quad ^{140}Te\;:\;8.3$$
3) Déterminer l'énergie libérée par 1 mole d'uranium $235.$
Données :
$\mathcal{N}=6.02\;10^{23}\;\text{mol}^{-1}$
$m_{\text{proton}}=m_{\text{neutron}}=1.67\;10^{-27}\;kg\;,\ m_{\left(_{\ 92}^{235}U\right)}=235.044\;\text{u}$
Résolution
1) L'énergie de liaison est donnée par : $$E_{\ell}=\Delta m\times c^{2}=Zm_{\text{proton}}+(A-Z)m_{\text{neutron}}-m\left(_{\ 92}^{235}U\right)\times c^{2}$$
A.N : $E_{\ell}=[92\times 1.67\;10^{-27}+(235-92)\times 1.67\;10^{-27}-235\times 1.66\;10^{-27}]\times(3\;10^{8})^{2}=2.79\;10^{-10}\;J$
Après conversion en $MeV$, on obtient : $\boxed{E_{\ell}=1743.75\;MeV}$
2) L'énergie libérée est donnée par : $$E_{\text{libérée}}=|E_{\text{produits}}-E_{\text{réactifs}}|=E_{Zr}+E_{Te}-E_{U}$$
A.N : $E_{\text{libérée}}=93\times 8.6+140\times 8.3-235\times 7.5=199.3$
Donc, $\boxed{E_{\text{libérée}}=199.3\;MeV}$
3) On sait qu'une mole d'uranium $235$ contient $\mathcal{N}$ noyaux.
Soit $E_{\text{mol}}$ l'énergie libérée par $1$ mole d'uranium $235$ alors on a : $$E_{\text{mol}}=E_{\text{libérée}}\times\mathcal{N}$$
A.N : $E_{\text{mol}}=199.3\times 6.02\;10^{23}=11.99\;10^{25}$
$\boxed{E_{\text{mol}}=11.99\;10^{25}\;MeV}$

Commentaires
Seynabou SENE (non vérifié)
sam, 08/15/2020 - 22:33
Permalien
trés bien expliqué , chapeau
Ajouter un commentaire