Vous êtes ici

Série d'exercices : Énergie électrique mise en jeu dans un circuit électrique - 1er s

Classe:

Première

Exercice 1

1. Définir : générateur, récepteur.

2. Citez un des dispositifs permettant de transformer l'énergie mécanique en énergie électrique.

3. Un générateur $G(e=15\,V$ ; $r=0.8)$ est monté en série avec électrolyseur $E(e'=1.8\,V$ ; $r'=4.3)$ et un résistance de résistance $R.$

3.1 Faire le schéma du montage.

Exprimer l'intensité $I$ en fonction de $e'$, $e$, $r'$, $r$ et $R$

3.2 Quelle est la valeur de $R$ si $I=2A.$

Calculer le rendement du générateur et le rendement de l'électrolyseur.

3.4 Calculer la puissance chimique (puissance utile) de l'électrolyseur et la puissance totale du générateur.

5.4 En $5$ minutes, quelle est l'énergie dissipée par effet Joule dans le circuit ?

Exercice 2

Un circuit comprend en série :

Un ampèremètre de résistance négligeable.

Un générateur de $f.c.é.m$ ; $E=12V$ de résistance interne $r=1\Omega.$

Un moteur de $f.c.é.m$ ; $E'$ de résistance interne $r'.$

Une résistance $R=10\Omega.$

Schématiser le circuit.

A l'aide d'un wattmètre en mesure la puissance mécanique $P_{méc}$ développée par le moteur en fonction de l'intensité $I.$

Justifier théoriquement, le résultat expérimental en donnant l'expression de la puissance mécanique développée par le moteur en fonction de l'intensité $I$ et la $f.c.é.m.$ $E'.$

D'après le graphique, calculer la $f.c.é.m.$ $E'$ du moteur.

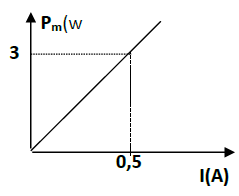
Calculer pour $I=2.5\,A$ et pendant $30\,mn$

1) L'énergie mécanique développée par le moteur.

2) L'énergie électrique consommée par le résistor résistance $R$

3) L'énergie électrique totale consommée par le moteur.

En déduire le rendement du moteur.

5) Calculer $r'$ la résistance interne de moteur.

Exercice 3

Un circuit comprend en série : un générateur de $f.é.m.$ $E'=24V$ et de résistance interne $r=2\Omega.$

Un resistor de résistance $R$ ; un ampèremètre de résistance négligeable ; un moteur de $f.c.é.m.$ $E'=12V$ et de résistance $r'$ et un interrupteur $K.$

Le montage comporte un voltmètre branché en parallèle avec le moteur.

On ferme l'interrupteur, le voltmètre indique une tension égale à $17V.$

Pour une durée de $5mn$, l'énergie thermique dissipée dans le moteur est égale à $5100\,j.$

1. Faire un schéma de circuit.

2.1 Montrer que l'ampèremètre indique un courant d'intensité $I=1\,A$

2.2 En déduire la résistance interne $r'$ du moteur.

2.3 Déterminer $R$

3. Déterminer, pour une durée de $5\,mn$ :

3.1 L'énergie électrique totale fournie par le générateur au circuit extérieur.

3.2 L'énergie thermique dissipée dans tout le circuit.

3.3 L'énergie mécanique et l'énergie électrique reçue par le moteur.

Exercice 4

Un moteur a les caractéristiques suivantes : résistance interne $r'=\Omega.$ $f.é.m.$ $E'=7.2V.$

Il est alimenté par un générateur de tension pour lequel $E=16.0\,V$ et $r=1.2\Omega$

1) Faire un schéma du circuit électrique comprenant le moteur et le générateur.

Préciser le sens du courant compte tenu de polarités du générateur et schématiser les tensions positives aux bornes du moteur et du générateur.

$-\ $ Placer sur le schéma un voltmètre et un ampèremètre permettant de mesurer l'intensité dans le circuit et la tension aux bornes du moteur.

2) Donner l'expression de l'intensité du courant $I$ en fonction de $E$, $r$, $E'$ et $r'.$

3) Calculer $I.$

4) Calculer :

$-\ $ La puissance électrique $P_{e}$ reçue par le moteur ;

$-\ $ La puissance mécanique $P_{m}$ développée par le moteur ;

$-\ $ La puissance $P_{j}$ dissipée par effet Joule dans l'ensemble du circuit.

5) Calculer :

$-\ $ Le rendement du générateur ; $\rho_{G}$

$-\ $ le rendement du moteur ; $\rho_{M}$

$-\ $ le rendement du circuit ; $\rho=\rho_{M^{\ast}}\rho_{G}$

Exercice 5 Transferts de puissance

un générateur de tension, de $f.é.m.$ $E$ et de résistance interne $r$, est relié à un récepteur, de $f.c.é.m.$ $E'$ et de résistance interne $r'.$

1.1 Faire le schéma du circuit électrique, en représentant les différentes tensions et l'intensité $I$ du courant électrique qui le parcourt.

1.2 Quelles sont les définitions de la $f.é.m.$ d'un récepteur ?

1.3 Donner l'expression de la tension aux bornes du générateur de tension en fonction de $E$, $r$, et $I.$

1.4 Donner l'expression de la tension aux bornes du récepteur en fonction de $ E'$, $r'$ et $I.$

1.5 En déduire l'expression de $I$ en fonction de $E$, $E'$, $r$ et $r'.$

2. On se place dans le cas ou $E'=0.$

2.1 Comment se comporte alors le récepteur ?

2.2 Donner l'expression de la puissance $P_{j}$ dissipée par l'effet Joule dans le récepteur en fonction de $E$, $r$, et $r'.$

2.3 Donner l'expression de la puissance $P_{géné}$ générée par le générateur de tension.

2.4 En déduire la définition, puis l'expression, du rendement global $\eta$ du circuit, appelé encore rendement encore rendement du transfert de puissance.

2.5 Pour quelle relation entre $r$ et $r'$ ce rendement $\eta$ est-il proche de $1.00$ ?

2.6 La puissance $P_{J}$ est maximale lorsque $r=r'.$

Donner, dans ce cas, les expressions de $P_{J}$ et de $P_{géné}$ puis la valeur numérique du rendement $\eta$ du transfert de puissance.

3. On suppose à présent que $E'\neq 0.$

3.1 Donner l'expression de $P_{géné}$ en fonction de $E$, $E'$, $r$ et $r'.$

3.2 Donner l'expression de la puissance utile $P_{u}$ convertie par le récepteur.

3.3 En déduire l'expression du rendement $\eta'$ du transfert de puissance du circuit.

Que se passe-t-il, du point de vue électrique, si $E'>E$ ?

3.4 Pour quelle condition entre $E$ et $E'$ ce rendement $\eta'$ est-il proche de $1.00$ ?

3.5 La puissance Pu passe par un maximum pour $E'=0.500\cdot E.$

Quelle est alors la valeur numérique du rendement $\eta'$ ?

Exercice 6

Un circuit série constitué :

$-\ $ Un générateur de $f.é.m.$ $E=24V$, de résistance interne $r=2\Omega.$

$-\ $ Un moteur électrique de $f.c.é.m$ $E'$ et de résistance interne $r'.$

$-\ $ Un résistor de résistance $R$ inconnue.

$-\ $ Un ampèremètre de résistance négligeable.

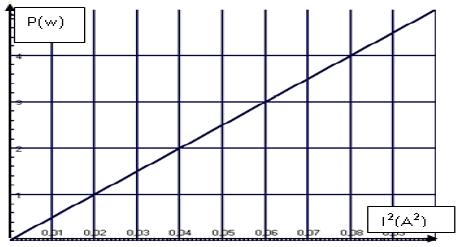
A l'aide d'un wattmètre on mesure la puissance électrique $P$ consommée par le résistor de résistance $R$ pour différentes valeurs de l'intensité.

Les résultats expérimentaux ont permis de tracer cette courbe. .

1) Justifier théoriquement la courbe obtenue

2) Déduire la valeur de $R.$

3) Calculer $I$ lorsque la puissance consommée par le résistor $P=2.25w.$

4) On fixe $I=0.2A$ ; calculer :

a) la puissance électrique totale fournie par le générateur au circuit extérieur.

b) la puissance consommée par le résistor.

c) la puissance électrique totale consommée par le moteur.

d) On définit le rendement $\rho$ du moteur $\rho=\dfrac{\text{Puissance mécanique}}{\text{Puissance totale consommée par le moteur}}$

On donne $\rho=92\%.$

Calculer :

$-\ $ La puissance mécanique développée par le moteur.

$-\ $ La $f.c.é.m$ $E'$ et la résistance interne $r'$ du moteur.

5) On remplace le résistor de résistance $R$ par un autre de résistance $R'$ supérieure à $R.$

Tracer sur la même feuille l'allure de la courbe représentative de la variation de la puissance électrique consommée par le résistor de résistance $R'$ et celle consommée par $R$ en fonction de $I^{2}$

Exercice 7

Un circuit électrique comprend en série :

$-\ $ Deux piles identiques chacune de $f.é.m.$ $E=12V$ et de résistance interne $r=1.$

$-\ $ Un résistor de résistance $R=5.$

$-\ $ Un moteur de $f.c.é.m$ $E'=12V$ et de résistance interne $r'.$

La tension aux bornes du moteur est égale à $17V$ et pour une durée de $5min$, l'énergie thermique dissipée dans le moteur est égale à $1500J.$

1) a) Déterminer l'intensité du courant dans le circuit.

b) En déduire la résistance interne $r'$ du moteur.

2) Déterminer, pour une durée de $5min$ :

a) L'énergie électrique totale fournie par les deux piles.

b) L'énergie thermique dissipée dans tout le circuit.

c) L'énergie mécanique et l'énergie électrique reçue par le moteur.

En déduire le rendement du moteur.

(On rappelle que le rendement d'un moteur est le rapport de son énergie mécanique par l'énergie électrique qu'il reçoit pendant la même durée).

Exercice 8

La caractéristique intensité-tension d'une pile de $f.é.m.$ $E$ et de résistance interne $r$ passe par les deux points $A(3.9V$ ; $0.3A)$ ; $B(3.5V$ ; $0.5A).$

1.1 Écrire l'expression de la tension $U_{PN}$ aux bornes de la pile lorsqu'elle débite un courant d'intensité $I.$

1.2 En déduire la valeur de $E$ et de $r.$

2. Calculer l'intensité $I$ du courant lorsque la tension aux bornes de la pile est $U_{PN}=2.5V.$

3. On associe en série $N$ piles identiques caractérisée chacune par sa $f.é.m.$ $E_{0}=4.5V$ et sa résistance interne $r_{0}=2\Omega.$

Le générateur équivalent a pour $f.é.m.$ $E=13.5V.$

3.1 Calculer le nombre $N$ des piles associées en série.

3.2 Calculer la résistance $r$ du générateur équivalent.

3.3 Ces $N$ piles montées en série sont branchées aux bornes d'un résister de résistance $R=50\Omega.$

$\bullet\ $ Faire un schéma du montage.

$\bullet\ $ Calculer l'intensité $I$ du courant dans le circuit.

Exercice 9

L'énergie thermique produite par un moteur pendant $1min.$ est $12\cdot10^{3}J$ quand il développe une puissance mécanique de $1000W.$

Calculer :

1) La puissance électrique transformée en puissance thermique dans le moteur.

2) La puissance électrique totale consommée par le moteur.

3) L'énergie électrique consommée par le moteur en $1h.$

4) Le rendement du moteur c'est à dire le rapport de la puissance mécanique qu'il fournit à la puissance électrique totale qu'il consomme.

Exercice 10

Un circuit électrique comprend ; associés en série ; deux piles identiques de $f.é.m.$ $E_{1}=E_{2}=E=4.5V$, de résistance interne $r_{1}=r_{2}=1.5\Omega$ et un moteur $M$, de $f.c.é.m.$ $'=5V$ et de résistance $r'=2\Omega.$

1) Peut-on associer les deux piles en parallèles pour alimenter le moteur ?

Justifier la réponse.

2) Faire un schéma du circuit qui permet au moteur de tourner en indiquant par des flèches le courant et les tensions aux bornes des dipôles.

3) Par application de la loi des mailles, donner l'expression de l'intensité du courant qui traverse le circuit.

La calculer.

4) Faire le bilan énergétique et calculer ces énergies électriques après une heure de fonctionnement.

On réalise le circuit électrique suivant où :

$-\ $ $G$ est un générateur de $f.é.m.$ $E$ et de résistance interne $r$ négligeable.

$-\ $ $M$ est un moteur de $f.c.é.m$ $E'=6V$ et de résistance interne $r'=2\Omega.$

Le générateur débite un courant d'intensité $I=2A$ pendant une durée de $10\,mn.$

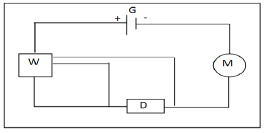
Pour mesurer la puissance électrique consommée par le dipôle $D$ on utilise un wattmètre $W.$

5. Rappeler l'expression de la puissance électrique consommée par un dipôle et donner la signification physique de chaque terme.

6. Sachant que le dipôle $D$ transforme entièrement l'énergie électrique qu'il reçoit en énergie thermique.

6.1 Donner la nature du dipôle $D.$

6.2 En déduire sa grandeur électrique caractéristique, sachant que le wattmètre indique $P=200W$

7.1 Déterminer l'énergie électrique $W_{1}$ consommée par le moteur pendant la durée de $10\,mn$

7.2 En quelles formes d'énergie, $W_{1}$ est-elle transformée ?

Déterminer la valeur de chacune de ces énergies.

8.1 Déterminer, pendant la même durée, l'énergie électrique produite par le générateur $G.$

8.2 En déduire la valeur de la $f.é.m.$ du générateur.

8.3 Retrouver, la valeur de E par application de la loi de Pouillet.

Exercice 11

On dispose en série un générateur $G_{1}$ $(E_{1}=12V$ ; $r_{1}=1\Omega)$, un résistor $R=5\Omega$, un moteur de $f.c.é.m$ $E'$ et de résistance interne $r'$ et un ampèremètre de résistance réglable.

1. Rappeler les lois d'ohm relatives à chaque dipôle.

2. L'ampèremètre indique $I_{1}=0A.$

Que peut-on dire de la $f.c.é.m$ $E'$ du moteur.

3. On remplace $G_{1}$ par un autre générateur $G_{2}$ $(E_{2}=16V$ ; $r_{2}=1.5\Omega).$

L'ampèremètre indique $I_{2}=0.6A.$

Si on enlève le résistor l'ampèremètre indique $I_{3}=1.8A.$

Déduire les valeurs de $E'$ et $r'.$

4. On associe $G_{1}$ et $G_{2}$ en série avec un moteur $(E'=11.5V$ ; $r'=1\Omega)$, un électrolyseur $(E'=10V$, $'=2\Omega)$ et $3$ résistors $R_{1}=R_{2}=R_{3}=5\Omega$

4.1 Déterminer le dipôle équivalent de l'association étudiée

4.2 Déterminer l'intensité du courant qui circule dans le circuit

Exercice 12

Un circuit électrique est constitué d'un générateur $G$ de $f.é.m.$ $E$ et de résistance interne $r$

I. Expérience 1 :

On branche aux bornes du générateur un résistor de résistance $R_{1}=4\Omega.$

Un ampèremètre placé en série dans le circuit indique $I_{1}=2A.$

II. Expérience 2 :

On branche aux bornes du générateur un résistor de résistance $R_{2}=1\Omega.$

L'ampèremètre indique $I_{2}=4A.$

1. Écrire la loi d'Ohm aux bornes de chaque dipôle.

2. Déterminer les grandeurs caractéristiques $(E$ ; $r)$ du générateur.

3. Le générateur $G$ précédent de $f.é.m$ $E$ et de résistance interne $r$ est placé dans un circuit formé par un ampèremètre en série avec un rhéostat de résistance variable.

Une étude expérimentale a permis de tracer la caractéristique intensité-tension du générateur.

(Voir figure)

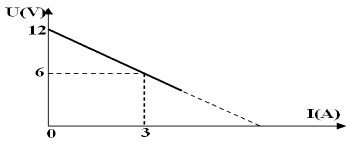
3.1 Représenter le schéma du circuit en indiquant les branchements de l'ampèremètre et du voltmètre dans le circuit.

3.2 A partir du graphe, retrouver les valeurs des grandeurs caractéristiques du générateur.

3.3 Déterminer graphiquement et par le calcul la valeur de l'intensité du courant électrique de court-circuit $I_{cc}$

4. On branche en parallèle avec le générateur $G$ un électrolyseur $(E'=8V$ ; $r'=2\Omega).$

4.1 En appliquant la loi de Pouillet, déterminer l'intensité du courant électrique qui circule dans le circuit.

4.2 Déduire les coordonnées du point de fonctionnement $P.$

Conclure quant à l'adaptation des deux dipôles.

Exercice 13 Fonctionnement d'une lampe de poche

On dispose d'une ampoule de lampe de poche, d'un générateur de tension continue de $f.é.m$ $E=4.5V$ et de résistance interne $r=1.5\Omega$, d'un rhéostat dont la valeur de la résistance peut varier de $0$ à $120\Omega$, de deux multimètres, d'un interrupteur et de fils de connexion.

On réalise le montage ci-dessous dans lequel la tension aux bornes de l'ampèremètre est négligeable

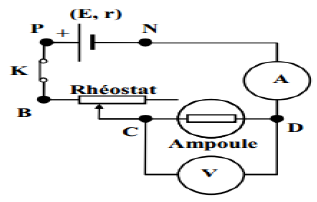
1) Comment peut-on faire varier l'intensité I du courant électrique dans le circuit ?

2) Recopier le schéma et placer le sens conventionnel du courant électrique ainsi que les bornes des appareils de mesure.

3) Quand l'intensité $I$ du courant électrique vaut $0.20A$, la tension $U_{CD}$ vaut $2.0V$

$-\ $ Calculer $U_{PN}$

$-\ $ Quelle est la valeur de la résistance $R$ du rhéostat ?

$-\ $ Quelle est la valeur $P_{1}$ de la puissance fournie par le générateur au circuit extérieur ?

$-\ $ Quelle est la puissance P2 dissipée par effet joule dans le générateur ?

4) On réalise une série de mesure de $U_{CD}$ en fonction de $I.$

Rappeler la relation donnant la puissance électrique $P_{3}$ consommée dans l'ampoule.

On trace le graphe de $P_{3}=f(U_{CD})$ :

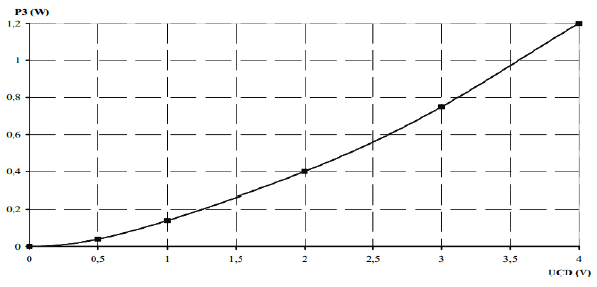
5) L'ampoule est utilisée dans une lampe de poche.

Elle consomme alors une puissance $P=1.0W.$

En utilisant le graphe précédent (à rendre avec la copie), déterminer la tension $U$ aux bornes de l'ampoule.

En déduire la valeur de l'intensité $I$ du courant électrique qui la traverse.

L'indication portée par l'ampoule : $1W$ ; $0.3A$ est-elle cohérente avec les résultats ?

Exercice 14 Caractéristique d'un électrolyseur

Un électrolyseur comportant deux électrodes $A$ et $B$ en fer contient une solution aqueuse d'acide sulfurique.

Il est monté en série avec un générateur de tension continue réglable et un ampèremètre.

Un voltmètre est placé aux bornes de l'électrolyseur.

1) Schématiser le montage en précisant le sens conventionnel du courant électrique et les bornes des appareils de mesure.

2) Une expérience a donné les résultats suivants :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline I(mA)&0&0&0&20&30&50&100&150&200&300&400\\ \hline U_{AB}(V)&0&0.50&1.50&1.60&1.70&1.80&2.00&2.10&2.25&2.50&2.75\\ \hline \end{array}$$

Représenter graphiquement la tension $U_{AB}$ en fonction de l'intensité $I$ du courant électrique.

Échelle :

en abscisse : $20mA/cm$

en ordonnée : $0.20V/cm$

3) La partie linéaire de la courbe est de la forme : $U=a+bI.$

Que représente $a$ ?

Que représente $b$ ?

Déterminer graphiquement $a$ et $b$ en détaillant soigneusement les calculs.

Donner l'équation numérique $U=f(I).$

4) Donner l'expression de la puissance électrique reçue par l'électrolyseur.

Calculer sa valeur pour $I=200mA.$

5) Quelle est l'énergie, exprimée en $kWh$, reçue par l'électrolyseur pendant une durée de fonctionnement de $5.0h$ ?