Série d'exercices : Équilibre d'un solide soumis à des forces - 2nd S
Classe:
Seconde
Exercice 1 : Équilibre d'un solide relié à un fil sur un plan incliné.
1) Un solide $S$ de poids $P=100\;N$ est maintenu en équilibre sur un plan incliné d'un angle $\alpha$ par rapport à l'horizontal grâce à un fil (figure.1 ci-dessous).
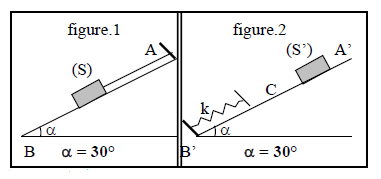
Le support du plan incliné $AB$ est lisse.
1.1) Faire le bilan des forces appliquées au solide $(S).$
1.2) Représenter ces forces puis déterminer leurs intensités par la méthode analytique.
2) Un solide $(S')$ de poids $P'$ glisse sur un support oblique $A'B'$ (figure.2 ci-dessus) .
La partie $A'C$ de ce plan est rugueuse et la partie $CB'$ lisse.
a) Le solide $S'$ s'arrête entre $A'\ $ et $\ C.$
Exprimer les composantes tangentielle $f$ et normale $R_{n}$ de la réaction du plan $A'C$ en fonction de $P'\ $ et $\ \alpha$
Comparer la direction de cette force de réaction à celle du vecteur poids du solide $S'.$
b) On déplace le solide $S'$ et on le pose sur le plan $CB'$ au-delà du point $C$ (figure.2).
Il glisse puis se met en contact avec un ressort de constante de raideur $k.$
Le solide $S'$ s'immobilise alors quand le ressort est comprimé d'une quantité $x.$
Représenter les forces s'exerçant sur le solide $S'$ dans cet état d'équilibre puis exprimer l'intensité de la force exercée par le ressort sur $S'$ en fonction de $P'\ $ et $\ \alpha.$
c) Considérant les résultats a) et b), exprimer l'intensité $f$ des forces de frottement du plan $A'C$ en fonction de $x$ et de $k.$
d) Calculer dans l'ordre $f\;,\ R_{n}$, la réaction $R$ du plan $A'C$, et la masse $m'$ du solide $S'.$
On donne : $k=50\;N.m^{-1}\;;\ g=10\;N.kg^{-1}\;;\ x=8\;cm\;;\ \alpha=30^{\circ}$
e) Calculer l'angle $\beta$ que fait la direction de la réaction du plan, $A'C$ avec celle du plan incliné $A'B'.$
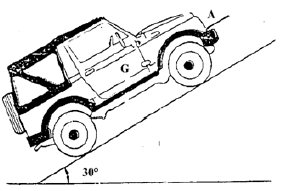
Exercice 2
Un véhicule de masse $820\;kg$ est immobilisé sur un plan incliné à l'aide d'un câble fixé au point $A.$
Les frottements sur le sol sont négligés. Le plan est incliné de $30^{\circ}$ par rapport au plan horizontal.
1) Faire le bilan des forces s'exerçant sur le véhicule;
2) Déterminer par méthode graphique les intensités des forces inconnues.
On prendra $g =10\;N.kg^{-1}$. Échelle : $1\;cm$ pour $2000\;N$
3) Retrouver ces intensités par méthode analytique
N.B : la réaction exercée par le sol sur le véhicule par l'intermédiaire des 4 roues est assimilée à une force unique appliquée en $G$ et de direction perpendiculaire au plan incliné
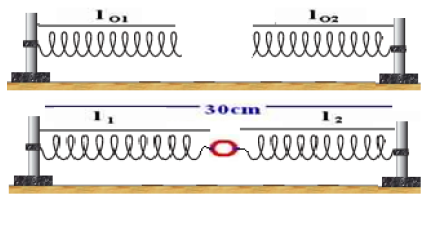
Exercice 3
On dispose de 2 ressorts . Le ressort $(R_{1})$ a une longueur à vide $l_{01}$ de $10\;cm$ et s'allonge de $1\;cm$ pour une force appliquée de $1\;N.$
Le ressort $(R_{2})$ a une longueur à vide $l_{02}=15\;cm$ et s'allonge de $4\;cm$ pour une force appliquée de $1\;N.$
On les réunit à un anneau de poids et de dimensions négligeables.
Les 2 autres extrémités des ressorts sont fixées à 2 crochets distants de $30\;cm.$
Soient $l_{1}\ $ et $\ l_{2}$ les longueurs respectives des ressorts $(R_{1})\ $ et $\ (R_{2}).$
Calculer de la longueur de chaque ressort $l_{1}\ $ et $\ l_{2}$ et les forces de tension $F_{1}\ $ et $\ F_{2}$ des ressorts
Exercice 4
On veut déterminer par le calcul la masse $m$ et l'angle $\alpha$, dans la situation décrite ci-dessous.
On a : $m_{1}=150\;g\;;\ m_{2}=100\;g\ $ et $\ \beta=90^{\circ}.$
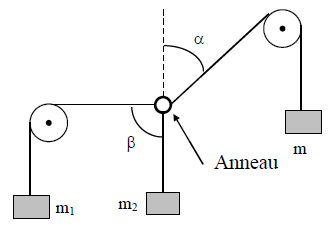
1) Représenter sur un schéma les forces qui s'exercent sur l'anneau
2) Rappeler la relation vectorielle que l'on peut écrire à l'équilibre.
3) Le plan est muni d'une base orthonormé ${O\;,\ \vec{i}\;,\ \vec{j}}.$
Donner l'expression de toutes les forces agissant sur l'anneau en fonction des vecteurs $\vec{i}\ $ et $\ \vec{j}$ de la base et de l'intensité de chacune des forces.
4) En déduire 2 équations permettant de calculer $\alpha\ $ et $\ m.$
5) Calculer $\tan\alpha$ pour en déduire la valeur de $\alpha$ puis de $m.$
6) Vérifier vos valeurs trouvées à celle qui sont mesurables expérimentalement.
Exercice 5
I) Un ressort à spires non jointives de longueur $L_{0}$ et de masse négligeable.
Dans le but de déterminer la raideur $K$ de ressort, on mesure sa longueur $L$ pour des valeurs différentes de la tension de ressort $T$ ; On donne la courbe suivante :
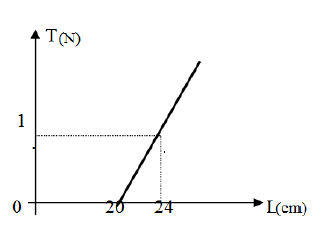
1) Donner l'expression de $T$ en fonction de $K\;,\ L\ $ et $\ L_{0}$
2) Déduire a partir du graphique : $T(N)$
a) La raideur $K$ du ressort en $N.m^{-1}$
b) La longueur $L_{0}$ du ressort en $cm$
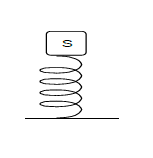
II) Le ressort précédent est disposé de la manière suivante :
A l'équilibre de solide la longueur du ressort est $l=18\;cm$ .
1) Représenter les forces exercées sur le solide a l'équilibre.
2) Calculer la tension du ressort.
3) En déduire la masse m du solide $(S).$ On donne $g=9.8\;N.kg^{-1}$
Exercice 6
Un corps $(C)$ de poids $P=20\;N$ repose sans frottement sur un plan incliné faisant un angle $\alpha=30^{\circ}$ par rapport à l'horizontale.
Il est maintenu fixe à l'aide d'un ressort de masse négligeable, de raideur $k=500\;N.m^{-1}$, de longueur initiale $L_{0}=20\;cm$ et faisant un angle $\beta=15^{\circ}$ par rapport au plan incliné.
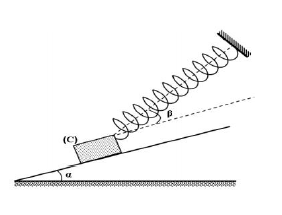
1) Représenter les forces exercées sur le corps $(C).$
2) Écrire la condition d'équilibre du corps $(C).$
3) Déterminer la valeur de la tension $T$ du ressort.
4) Déduire sa longueur $L.$
5) En réalité les frottements ne sont pas négligeables et sont équivalentes à une force $f$ parallèle au plan incliné et dirigée vers le haut.
La valeur de la tension du ressort est dans ce cas $T'=8.4\;N$
Écrire la nouvelle condition d'équilibre du corps $(C)$ et déduire la valeur de la force de frottement $f$
Exercice 7
I) Soit un ressort à spires non jointives, de longueur initiale $L_{0}$ et de masse négligeable
Afin de déterminer sa raideur K on accroche un solide $(S_{1})$ de masse $m_{1}=100\;g$, la longueur de ressort est $L_{1}=20\;cm.$
On remplace $(S_{1})$ par un solide $(S_{2})$ de masse $m_{2}=175\;g$ la longueur de ressort devient $L_{2}=23\;cm$
1-a) Établir l'expression de K en fonction de $m_{1}\;;\ m_{2}\;;\ g\;;\ L_{1}\ $ et $\ L_{2}$
Montrer que $K=\dfrac{(m_{2}-m_{1})}{l_{2}-l_{1}}g$
Calculer sa valeur en $N.m^{-1}$
b) En déduire la longueur initiale $L_{0}$ du ressort.
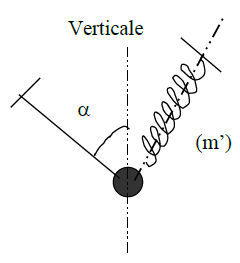
II) Avec le ressort précédent, on réalise le système schématisé ci-dessous ; le solide $(S')$ de masse $m'$ est accroché d'une part au ressort, d'autre part à un fil (voir figure).
A l'équilibre, la direction de fil fait un angle $\alpha=60^{\circ}$ avec la verticale d'une part et d'autre part elle est perpendiculaire à celle de l'axe du ressort. Soit $L=18\;cm$ ; la longueur de ressort à l'équilibre.
1) Représenter toutes les forces exercées sur $(S')$
2) Établir en fonction de $m'\;,\ g\ $ et $\ \alpha$
2.1) La tension de ressort $T_{1}$
2.2) La tension du fil $T_{2}$
2.3) Calculer leurs valeurs
3) En déduire la masse $m'$ de solide $(S')$
Exercice 8
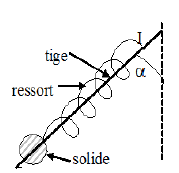
Une tige rigide est maintenue incliné d'un angle $\alpha=60^{\circ}$ par rapport à la verticale.
Un ressort à spires non jointives, de masse négligeable de longueur à vide $L_{0}=12\;cm$, de raideur $k=50N.m^{-1}$ est enfilé le long de la tige.
L'une des extrémités de la tige est fixé en un point $I$ de la tige, l'autre extrémité est attachée à un solide de masse $m=80\;g$ (voir figure)
1) Représenter toutes les forces appliquées au solide.
2.a) Exprimer la tension du ressort en fonction de $m\;,\ g\ $ et $\ \alpha.$
Calculer sa valeur. On prendra $g=9.8N.kg^{-1}$
On donne : $\sin\alpha=0.86\ $ et $\ \cos\alpha=0.5$
b) En déduire la valeur de l'allongement du ressort a l'équilibre.
3) Exprimer la réaction $R$ de la tige en fonction de $m\;,\ g\ $ et $\ \alpha.$ Calculer sa valeur
Exercice 9
1) un ressort à spires non jointives de longueur $L_{0}=20\;cm$ de masse négligeable et de raideur $k=25\;N.m^{-1}.$
Ce ressort disposé verticalement est fixé par son extrémité supérieure, à son extrémité inférieure, on suspend un solide de masse $m=100\;g.$
Déterminer la longueur $L$ du ressort à l'équilibre de solide.
2) le ressort et le solide précédent sont placés comme l'indique la figure.
on suppose que le solide repose sans frottement appréciable sur le plan incliné d'un angle $\alpha$ par rapport à la direction verticale.
L'axe de ressort est parallèle à la ligne de plus grande pente de plan incliné.
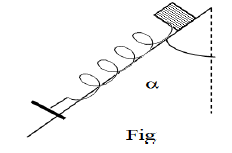
a) représenter toutes les forces extérieures agissant sur le solide.
b) calculer la tension de ressort sachant que la longueur de ressort a l'équilibre est $L=18\;cm.$
c) Établir les expressions de la tension de ressort ainsi que la réaction $R$ de plan en fonction de : $m\;,\ g\ $ et $\ \alpha.$ Calculer $\alpha\ $ et $\ R.$
On donne :
$g=10Nkg^{-1}\;;\ \cos60=0.5\;;\ \sin60=0.86\;;\ \cos30=0.86\;;\ \sin30=0.5$
3) On ajoute au solide précédent un solide $(S')$ de masse $(m').$
La longueur du ressort devient $L’=16.5\;cm$. Déterminer $m'.$
Exercice 10
Une charge de masse $m=50\;kg$ est suspendue au plafond à l'aide de 2 fils.
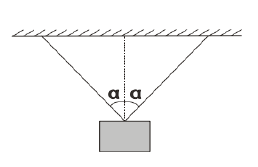
1) Faire le bilan des forces qui s'appliquent à la charge
2) Déterminer la tension dans chaque fil pour $\alpha=30^{\circ}\ $ et $\ \alpha=70^{\circ}.$
Exercice 11
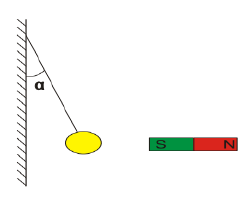
Une petite bille d'acier, de poids $P=5.10^{-2}\;N$, est attachée à un support vertical par un fil de nylon $AO$
En outre, un aimant exerce sur elle une force magnétique horizontale attractive.
A l'équilibre, le fil est incliné d'un angle $\alpha=20^{\circ}.$
Calculer l'intensité de la force magnétique ainsi que la valeur de la tension du fil.
Exercice 12
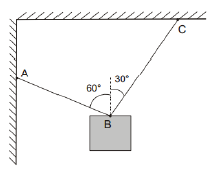
Une charge de poids $P=100\;N$ est soutenue par 2 fils $AB\ $ et $\ BC$ qui font respectivement, avec la verticale, des angles de $60^{\circ}\ $ et $\ 30^{\circ}.$
Calculer les tensions des 2 fils à l'équilibre
Exercice 13
Deux objets sont suspendus par l'intermédiaire de deux fils 1 et 2.
On donne : masse de $(S_{1})=1\;kg$ et masse de $(S_{2})=2\;kg$ ; la masse des fils est négligeable.
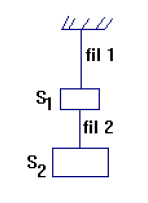
1) Déterminer à l'équilibre la tension du fil 2.
2) Déterminer à l'équilibre la tension du fil 1
Exercice 14
Un cube homogène, d'arête a égale à $10\;cm$, est fabriqué dans un matériau de masse volumique $\rho_{c}$, immergé dans l'eau et suspendu à un ressort vertical en $B$, le centre d'une face ; il est en équilibre.
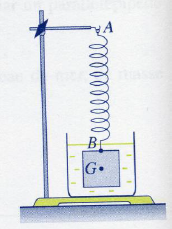
1) Déterminer les valeurs du poids $P$ du cube et de la poussée d'Archimède $F$ exercée par l'eau sur le solide.
2) Le solide étant en équilibre, les forces extérieures appliquées à ce cube sont colinéaires et leur direction passe par $G$ centre d'inertie du cube.
Déterminer la valeur de la force de rappel $T$ du ressort.
3) Déterminer l'allongement du ressort.
Données : $g=10\;N.kg^{-1}\;;\ \rho_{c}=9.10^{3}kg.m^{-3}\;;\ k=100\;N.m^{-1}$
Exercice 15
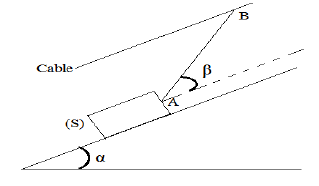
Un solide $(S)$, homogène de masse $100\;kg$ est maintenu en équilibre sur un plan incliné rugueux d'un angle $\alpha=30^{\circ}.$ par rapport au plan horizontal,
Le solide est plus relié à un câble par un fil AB faisant un angle, $\beta=25^{\circ}$ avec la ligne de grande pente.
Les forces de frottements sont modélisées par le vecteur $\vec{f}$, parallèle à la ligne et d'intensité $f=20\;N.$
1) Faire le bilan des forces s'exerçant sur le solide $(S)$
2) Représenter qualitativement ces forces sur la figure
3) Déterminer l'intensité de la tension du fil $AB$
4) Calculer la réaction du plan incliné et donner sa direction

Commentaires
Raphael (non vérifié)
mar, 11/03/2020 - 18:24
Permalien
Telecharger les exercices
Raphael (non vérifié)
mar, 11/03/2020 - 18:42
Permalien
Télécharger les exercices
Raphaël Kom (non vérifié)
mar, 11/03/2020 - 18:48
Permalien
Télécharger les exercices
Ntotokolo Rémy (non vérifié)
sam, 01/07/2023 - 07:42
Permalien
Besoin d'exercices
DOH grâce (non vérifié)
dim, 01/03/2021 - 23:45
Permalien
Être 1er de Ma classe
Tuo Adiaratou (non vérifié)
sam, 02/20/2021 - 10:32
Permalien
Exercice et corrige
Mody abdoullaye... (non vérifié)
mer, 04/28/2021 - 08:23
Permalien
Mauritanie
Pathe (non vérifié)
sam, 05/01/2021 - 23:38
Permalien
Ghhh
Issa (non vérifié)
mer, 10/20/2021 - 03:04
Permalien
Apprendre
Thierno Amadou ... (non vérifié)
dim, 04/24/2022 - 18:11
Permalien
Être premier de ma classe
Tekessa nacir (non vérifié)
jeu, 01/12/2023 - 21:51
Permalien
Devenir un scientifique
Tekessa nacir D... (non vérifié)
jeu, 01/12/2023 - 21:56
Permalien
Devenir un scientifique
Mariama (non vérifié)
dim, 02/25/2024 - 23:03
Permalien
Apprendre les mathématiques et le physique chimie
Gamael (non vérifié)
mer, 02/24/2021 - 14:53
Permalien
Pour me perfectionner
Guei Noël (non vérifié)
mer, 03/10/2021 - 08:56
Permalien
Besoin des séries d'exercices
Guei Noël (non vérifié)
mer, 03/10/2021 - 08:56
Permalien
Besoin des séries d'exercices
Alladoum Ernest (non vérifié)
mar, 03/29/2022 - 14:44
Permalien
Support comme exercices
Anonyme (non vérifié)
jeu, 12/01/2022 - 21:03
Permalien
Les sujets sont intérressents
Alladoum Ernest (non vérifié)
mar, 03/29/2022 - 14:45
Permalien
Support comme exercices
Lamarana Barry (non vérifié)
dim, 05/15/2022 - 14:57
Permalien
Connaissance
Mahamadou Gano (non vérifié)
lun, 05/16/2022 - 10:55
Permalien
Mécanique
N'dri kouassi joël (non vérifié)
mar, 12/06/2022 - 00:50
Permalien
C'est d'aller en classe supérieure
Tracy (non vérifié)
mer, 01/08/2025 - 21:49
Permalien
Je veux que vous m'aidez à comprendre afin d'avoir de bonnes no
Fassia Olivier (non vérifié)
dim, 01/28/2024 - 13:44
Permalien
Télécharger
Anonyme (non vérifié)
lun, 03/25/2024 - 19:27
Permalien
les exercices de l'équilibre d'un corps soumis des forces
Abdoul Fataho D... (non vérifié)
sam, 12/28/2024 - 01:22
Permalien
PHYSIQUE CHIMIE
Azmi (non vérifié)
dim, 02/16/2025 - 15:11
Permalien
Ex
Saad hamzy (non vérifié)
jeu, 02/25/2021 - 00:08
Permalien
Excellent
Alioune ndaw (non vérifié)
mer, 04/14/2021 - 15:40
Permalien
Pc
Mouhamed diaw (non vérifié)
mar, 07/13/2021 - 22:51
Permalien
Beugeu reussir .
Ndoman (non vérifié)
jeu, 12/16/2021 - 16:05
Permalien
Professeur
Anonyme (non vérifié)
jeu, 12/30/2021 - 11:32
Permalien
Téléchargez
Ouatfamo10@gmail.com (non vérifié)
jeu, 12/30/2021 - 11:32
Permalien
Exercices
Ouatfamo10@gmail.com (non vérifié)
jeu, 12/30/2021 - 11:37
Permalien
Exercices
Mht nour (non vérifié)
mar, 03/22/2022 - 17:14
Permalien
Recherche scientifique
Adja Maréme fall (non vérifié)
lun, 03/28/2022 - 23:51
Permalien
Des séries d'exercices PC
Abakar zene sou... (non vérifié)
sam, 04/02/2022 - 12:58
Permalien
Plan incliné
Ayouba (non vérifié)
jeu, 11/10/2022 - 09:10
Permalien
correction des exercices
Aicha fall (non vérifié)
dim, 01/01/2023 - 22:14
Permalien
Amélioration
Kendrich MANKOU (non vérifié)
lun, 01/16/2023 - 18:15
Permalien
Avis sur le site
Fatimata Sow (non vérifié)
mer, 02/01/2023 - 21:38
Permalien
Élève
ndèye mayane ngom (non vérifié)
dim, 03/12/2023 - 18:44
Permalien
exercice corriger
Rivo (non vérifié)
mar, 11/28/2023 - 09:32
Permalien
exercices très intéressants
Anonyme (non vérifié)
dim, 01/05/2025 - 20:10
Permalien
excellent
Ajouter un commentaire