Vous êtes ici

Série d'exercices : Cinématique - Ts

Classe:

Terminale

Exercice 1

Un mobile

$M_{1}$ est en mouvement relativement au repère d'espace

$\mathcal{R}(O\;,\ \vec{i}\;,\ \vec{j})$ , son vecteur vitesse est :

$\overrightarrow{V}_{1}=3\vec{i}+(-2t+4)\vec{j}$

1) Donner les lois horaires du mouvement sachant qu'à l'origine des temps, le mobile passe par l'origine

$O.$

2) Établir l'équation cartésienne de la trajectoire.

3) Établir l'expression du vecteur accélération

$\overrightarrow{\alpha}_{1}.$

Le représenter sur la trajectoire de la figure.

4) A quelle date la direction du vecteur vitesse est horizontale ?

En déduire les coordonnées

$(x_{s}\ ;\ y_{s})$ du sommet S de la trajectoire ainsi que la valeur de la vitesse en ce point.

Représenter ce vecteur vitesse.

5) Calculer :

Le rayon de courbure de la trajectoire à la date

$t=2s.$

L'abscisse

$x_{p}$ du mobile lorsque celui-ci repasse par l'ordonnée

$y=0.$

La valeur de la vitesse

$\overrightarrow{V}_{p}$ du mobile en ce point.

6) Un deuxième mobile

$M_{2}$ en mouvement rectiligne uniformément varié sur l'axe

$(ox)$ du repère

$\mathcal{R}(O\;,\ \vec{i}\;,\ \vec{j})$ , passe par le point d'abscisse

$x=20\,m$ à l'instant

$t=0$ avec une vitesse

$\overrightarrow{V}_{O_{2}}=2\vec{i}$

Déterminer la valeur algébrique de l'accélération du mobile

$M_{2}$ au point du rencontre avec

$M_{1}$ pour

$x=12\;m$

Exercice 2

Dans un repère

$(O\;,\ \vec{i}\;,\ \vec{j})$ orthonormé, les lois horaires du mouvement d'un mobile ponctuel

$M$ sont données par :

$x=t$ et

$y=\dfrac{t^{2}}{2}$ le temps est mesuré en secondes et les distances en mètres.

$t=0s$ le mobile débute son mouvement.

1) a) Quel est le point de départ du mobile à l'origine des dates ?

b) Établir l'équation de la trajectoire du mobile relativement au repère

$(O\;,\ \vec{i}\;,\ \vec{j}).$

c) Déterminer l'expression du vecteur vitesse et celle du vecteur accélération du mobile

$M.$

2) a) A quelle date le vecteur vitesse est colinéaire à

$\vec{i}$ ?

b) Montrer qu'à cette date la composante tangentielle de l'accélération est nulle.

3) Sachant, qu'à une date

$t$ , l'accélération tangentielle a pour expression

$\alpha_{T}=\dfrac{t}{\sqrt{1+t^{2}}}$ dans le repère de Frenet

$(M\;,\ \overrightarrow{T}\;,\ \overrightarrow{N})$ .

a) Montrer que celle de l'accélération normale est

$\alpha_{N}=\dfrac{1}{\sqrt{1+t^{2}}}.$

b) A quelle date

$t_{1}$ ,

$V_{x}=V_{y}$ avec

$V_{x}$ et

$V_{y}$ les composantes du vecteur vitesse dans le repère

$(O\;,\ \vec{i}\;,\ \vec{j})$ ?

c) Calculer le rayon de courbure à la date

$t_{1}.$

Exercice 3

Dans un repère

$\mathcal{R}=(O\;,\ \vec{i}\;,\ \vec{j})$ , un point mobile

$M_{1}$ est animé d'un mouvement rectiligne uniformément varié d'accélération

$a_{1}=-2\,m\cdot s^{-1}.$

A la date

$t_{1}=1\,s$ , le mobile

$M_{1}$ passe par le point

$A$ d'abscisse

$x_{A}=0\,m$ avec une vitesse

$V_{A}=6\,m\cdot s^{-1}.$

Sachant que le mobile débute son mouvement à la date

$t=0s.$

1) Déterminer la vitesse initiale et l'abscisse initiale du point mobile

$M_{1}.$

2) Écrire la loi horaire

$x_{1}(t)$ de mouvement de

$M_{1}.$

Déduire l'expression de sa vitesse instantanée.

3) Montrer que le mouvement de

$M_{1}$ comporte deux phases.

4) Calculer la distance parcourue par le mobile entre les dates

$t_{1}=1\,s$ et

$t_{2}=7\,s.$

Exercice 4

Les équations horaires du mouvement d'un mobile

$M$ relativement à un repère d'espace

$\mathcal{R}$

$(O\;,\ \vec{i}\;,\ \vec{j})$ sont

$x=2t$ et

$y=f(t)$

$(t>0).$

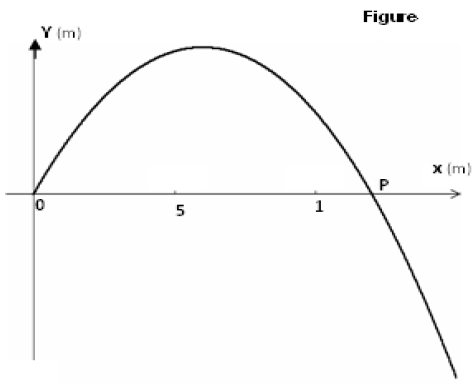
L'équation cartésienne de la trajectoire est

$y=-\dfrac{5}{4}x^{2}+2x.$

1) Représenter l'allure de la trajectoire.

2) Déterminer l'expression de l'ordonnée

$y=f(t)$ du mobile.

2) a) Déterminer les composantes du vecteur vitesse

$\overrightarrow{V}$ en fonction du temps.

2) b) à quelle date la direction du vecteur vitesse est horizontale, en déduire les coordonnées du sommet

$S$ de la trajectoire.

Calculer la valeur de la vitesse en ce point.

3) Donner l'expression du vecteur accélération

$\vec{a}.$

Conclure.

4) Calculer le rayon de courbure de la trajectoire au sommet

$S$ de la trajectoire.

5) Déterminer les phases du mouvement.

6) Déterminer l'abscisse du point

$P$

$(P\neq O)$ intersection de la trajectoire avec l'axe

$ox.$

Quelles sont les caractéristiques du vecteur vitesse

$\overrightarrow{V}_{p}$ en ce point ?

Comparer ce vecteur au vecteur

$\overrightarrow{V}_{O}$ (direction, valeur).

Représenter ces deux vecteurs sur la trajectoire.

(Échelle de votre choix).

Exercice 5

Un mobile

$M$ décrit une trajectoire rectiligne dans un repère

$(O\ ;\ \vec{i})$ ; son vecteur accélération est constant pendant toute la durée de son mouvement dans l'intervalle de temps

$[0\ ;\ 5s].$

A l'origine du temps, le mobile

$M$ part de la position d'abscisse

$x_{0}=0.5\,m$ avec une vitesse

$v_{0}=-1\,m\cdot s^{-1}$ , puis il passe par le point d'abscisse

$x_{1}=5m$ avec une vitesse

$v_{1}=4.7\,m\cdot s^{-1}.$

1) Calculer l'accélération

$a$ du mouvement.

2) Établir l'expression de la vitesse instantanée

$v(t)$ du mobile.

3) Déduire l'instant pour lequel le mobile passe par le point d'abscisse

$x_{1}.$

4) Établir l'équation horaire du mouvement.

5) Après deux secondes du départ du mobile

$M$ , un deuxième mobile

$M'$ part du point d'abscisse

$x=5m$ , en mouvement rectiligne uniforme de vitesse

$v'=4m\cdot s^{-1}.$

a) Déterminer l'équation horaire du mouvement du mobile

$M'$

b) Calculer la date

$t$ de rencontre des mobiles.

c) Calculer l'abscisse

$x$ correspondant à cette rencontre.

Exercice 6

Un mobile parcourt une distance

$AB=300m$ en deux phases.

$-\$

$1^{ière}$ phase : mouvement rectiligne uniformément accéléré d'accélération

$a_{1}=2\,m\cdot s^{-2}$

$-\$

$2^{ième}$ phase : mouvement rectiligne uniformément retardé d'accélération

$a_{2}=-1m\cdot s^{-2}.$

$t=Os$ le mobile part du point

$A$ , pris comme origine des espaces, sans vitesse initiale et arrive au point

$B$ avec une vitesse nulle

1) Soit

$C$ le point ou le mouvement devient retardé :

a) Exprimer, pour la

$1^{ière}$ phase,

$x_{C}$ en fonction de

$V_{C}$ et

$a_{1}.$

b) Exprimer, pour la

$2^{ième}$ phase,

$V_{C}$ en fonction de

$a_{2}$ ,

$x_{B}$ et

$x_{C}.$

c) Déduire d'après a) et b) l'expression de

$V_{C}$ en fonction de

$a_{1}$ ,

$a_{2}$ et

$x_{B}.$

Calculer sa valeur

2) a) Calculer la distance parcourue

$AC$ pendant la

$1^{ière}$ phase.

b) Calculer sa durée.

3) a) Déduire la distance parcourue

$CB$ pendant la

$2^{ième}$ phase.

b) Calculer la durée du trajet

$AB.$

Exercice 7

Un solide supposé ponctuel est attaché à un ressort à l'instant

$t=0s$ ; le solide est ramené au point d'abscisse

$x_{0}$ ; on lui communique une vitesse

$\overrightarrow{V}_{0}$ et on l'abandonne à lui-même, il effectue donc un mouvement rectiligne sinusoïdal dont l'enregistrement est donné par la figure suivante.

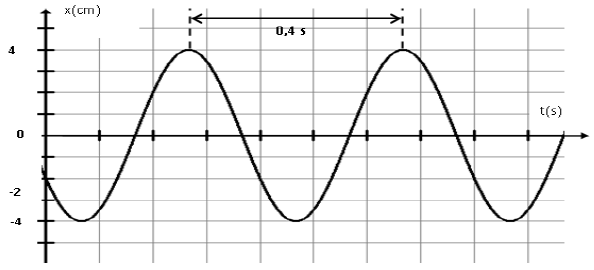
1) a) En exploitation l'enregistrement déterminer :

$-\$ la pulsation du mouvement

$\omega.$

$-\$ l'élongation initiale

$x_{0}.$

$-\$ l'amplitude

$X_{m}.$

$-\$ la phase initiale

$\varphi.$

b) En déduire la loi horaire

$x=f(t).$

2) a) Déterminer l'expression de la vitesse en fonction du temps.

b) En déduire la valeur algébrique de la vitesse initiale

$\overrightarrow{V}_{0}.$

3) A l'instant

$t_{1}>0$ ; le mobile repasse pour la première fois par la position d'abscisse

$x_{0}$ dans le sens négatif.

a) Déterminer graphiquement

$t_{1}.$

b) Retrouver

$t_{1}$ par le calcul.

4 Déterminer la valeur algébrique de la vitesse du solide lors de son premier passage par la position d'abscisse

$x=2\,cm.$

Exercice 8

Un point mobile

$M$ est animé d'un mouvement circulaire accélération angulaire est

$\ddot{\theta}=-\dfrac{\pi}{5}rad\cdot s^{-2}$ entre les instants

$t_{0}=0s$ et

$t_{1}=20s$ .

Le rayon de sa trajectoire est

$R=25\,cm.$

A l'origine des dates,

$M$ part de la position d'abscisse angulaire

$\dfrac{\pi}{3}$ avec une vitesse angulaire initiale

$\dot{\theta}_{0}=2\pi\;rad\cdot s^{-1}.$

1) Quelle est la nature de mouvement du mobile.

2) Donner les expressions de sa vitesse angulaire

$\dot{\theta}$ et de son élongation angulaire

$\theta$ en fonction du temps.

3) a) Montrer que ce mouvement comporte deux phases.

b) Déterminer le nombre de tours effectué par le mobile pendant la première phase du mouvement.

4) Calculer à la date

$t_{1}$

a) La vitesse angulaire

$\dot{\theta}_{1}$ ainsi que la vitesse linéaire du mobile.

b) l'accélération normale et l'accélération tangentielle du mobile.

Déduire la valeur de son accélération linéaire.

5) A partir de la date

$t_{1}$ , le mouvement du mobile

$M$ est circulaire uniforme à la vitesse angulaire

$\dot{\theta}_{1}.$

Calculer :

a) La période de ce mouvement.

Déduire sa fréquence.

b) Montrer que l'accélération linéaire d'un mouvement circulaire uniforme est égale à l'accélération normale.

Exercice 9

Une automobile se déplace sur une route horizontale à la vitesse constante de valeur

$\|\overrightarrow{V}_{0}\|=16\,m\cdot s^{-1}.$

Lorsqu'elle est à une distance

$d=200\,m$ du feu, le feu vert s'allume et reste pendant

$11s.$

Dans tout l'exercice, on prendra comme origine des temps

$(t=0s)$ , l'instant où le feu vert s'allume et l'origine des espaces

$(x_{0}=0\,m)$ , la position de la voiture à cet instant.

Le sens positif est le sens du mouvement.

1) A partir de l'instant de date

$t=0s$ , l'automobiliste accélère et impose à sa voiture une accélération constante.

A l'instant

$t_{1}$ , sa vitesse prend la valeur

$v_{1}=21\,m\cdot s^{-1}.$

Entre

$t=0s$ et

$t_{1}$ , l'automobiliste parcourt

$100\,m.$

a) Déterminer l'accélération

$a_{1}.$

b) Déterminer la date

$t_{1}.$

c) Écrire la loi horaire du mouvement de la voiture pour

$t\in[0\;,\ t_{1}].$

2) A partir de l'instant

$t_{1}$ , l'automobiliste maintient sa vitesse constante.

a) Écrire la loi horaire du mouvement de la voiture pour

$t\geq t_{1}.$

b) La voiture passe-t-elle devant le feu lorsqu'il est vert ?

Justifier la réponse

3) Si l'instant

$t_{1}$ , l'automobiliste freine et impose à sa voiture un mouvement uniformément retardé d'accélération

$a_{2}=-2\,m\cdot s^{-2}$

a) Calculer la distance parcourue par la voiture du début de freinage jusqu'à son arrêt

b) Déterminer la vitesse

$v_{2}$ de la voiture en passant devant le feu et la date

$t_{2}$ correspondante à ce passage.

c) Vérifier que la voiture est passée lorsque le feu n'est plus vert.

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Commentaires

Mamadou (non vérifié)

mar, 10/13/2020 - 17:52

Permalien

Comprendre la cinématique

Pour bien comprendre la cinématique

répondre

Awa (non vérifié)

mer, 11/25/2020 - 19:06

Permalien

Exercise

Comment montrer que la trajectoire est plane

répondre

zimo (non vérifié)

mer, 01/20/2021 - 00:23

Permalien

sujet

recevoir des exercice et corrigé

répondre

Eugène balamou (non vérifié)

mar, 06/11/2024 - 14:51

Permalien

Baccalauréat

J'ai besoin de votre aide s'il te plait je me prépare pour le baccalauréat mais j'ai quelques inquiétudes au niveau cinématographique

répondre

Bineta (non vérifié)

mar, 11/07/2023 - 07:03

Permalien

Compprendre la cinématique d'un point

A travers des explications claire et nette je veux comprend la cinématique d'un point

répondre

Anonyme (non vérifié)

dim, 11/07/2021 - 12:12

Permalien

Merci

répondre

Sallah (non vérifié)

mer, 11/02/2022 - 04:59

Permalien

Science

Pour avancer

répondre

Sallah (non vérifié)

mer, 11/02/2022 - 05:05

Permalien

Pour aprande

J'ai la sciences

répondre

meier (non vérifié)

lun, 11/14/2022 - 17:29

Permalien

kpjn,opkkln oj,ol,

répondre

Murat David Junior (non vérifié)

mer, 09/27/2023 - 00:55

Permalien

Salutation

Je viens de commencer avec la physique cinématique histoire de mieux savoir les phénomènes de la Nature qui adviennent et trouver des poins de repères et sa trajectoire Durant des nombreuses années.

répondre

Murat David Junior (non vérifié)

mer, 09/27/2023 - 00:56

Permalien

Re salutation

Points

répondre

Ngambomi (non vérifié)

dim, 10/08/2023 - 00:04

Permalien

Sujet

Je suis un élève je viens au près de vou pour avoir au moins un aide à la science physique car je sais que au de vous je trouverai les solutions des exercices

répondre

Merci (non vérifié)

ven, 10/20/2023 - 07:41

Permalien

Sciences physiques et mathématiques

Je suis élève de la terminale D Je viens en ce jour très particulier vous implorez votre aide qur ces deux matière! Merci beaucoup

répondre

Fofana (non vérifié)

mer, 11/08/2023 - 00:38

Permalien

Comprendre les cours de physique

Je suis vraiment content de votre cours ça me permet de comprendre un peu un peu les cours de physique donc merci bcp Et j'aimerais que vous m'envoyez une notification en cas d'une mise à jour de vos cours.