Série d'exercices : Dipôles passifs - 2nd S

 

1) Représenter l'allure de la caractéristique intensité-tension d'un dipôle :

 

a) dipôle symétrique passif.

 

b) dipôle asymétrique passif.

 

c) dipôle actif.

 

2) Comment varie la résistance d'un fil conducteur :

 

a) avec sa section.

 

b) avec sa longueur.

 

On donne les caractéristiques intensité-tension respectives des dipôles $D_{1}\;,\ D_{2}\ $ et $\ D_{3}.$

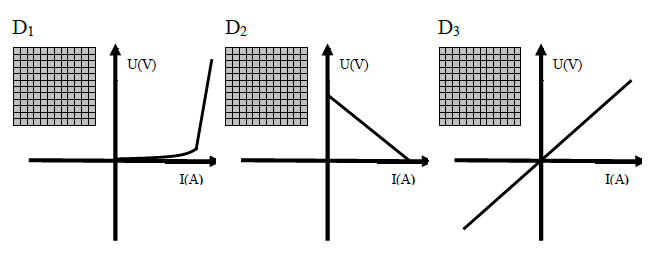
Compléter le tableau suivant :

 

$$\begin{array}{|l|c|c|c|}\hline\text{Dipôle}&D_{1}&D_{2}&D_{3}\\ \hline\text{Symétrique/Asymétrique}&&&\\ \hline\text{Linéaire/Non linéaire}&&&\\ \hline\text{Actif/Passif}&&&\\ \hline \end{array}$$

On réalise le montage suivant :

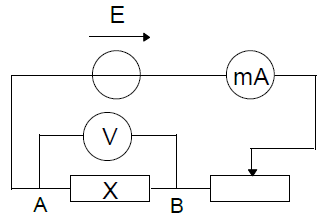
1) L'ampèremètre affiche $7.13\;mA$ et le voltmètre indique $3.29\;V$

 

Quelle est la résistance $X$ du conducteur ohmique placé entre $A\ $ et $\ B\ ?$

 

2) On déplace le curseur du rhéostat de sorte que le voltmètre affiche $2.03\;V$

 

Quelle est alors l'indication de l'ampèremètre ?

 

3) On déplace le curseur du rhéostat de sorte que l'ampèremètre indique $5.12\;mA$

 

Quelle est alors l'indication affichée par le voltmètre ?

 

On a relevé quelques points de fonctionnement d'une lampe à incandescence à filament métallique, normalement utilisé sous une tension de $6\;V$

 

$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|}\hline U(V)&0.05&0.1&0.3&0.4&0.6&0.8&2&3&4&5&6&7\\ \hline I(mA)&25&50&100&111&129&148&240&295&345&395&435&475\\ \hline \end{array}$$

 

1) Tracer la caractéristique intensité tension de la lampe.

 

2) Déterminer, pour chaque point de fonctionnement la résistance $R$ de la lampe.

 

Représenter graphiquement la relation $R=f(U.I)$

 

Que peut-on dire de la variation de la résistance $R$ du filament avec la température ?

 

3) Il est possible de linéariser la caractéristique entre les points de fonctionnement $(3\;V\;,\ 295\;mA)\ $ et $\ (7\;V\;,\ 475\;mA)$

 

Déterminer la relation affine qui décrit approximativement le fonctionnement de la lampe dans ce domaine d'utilisation

 

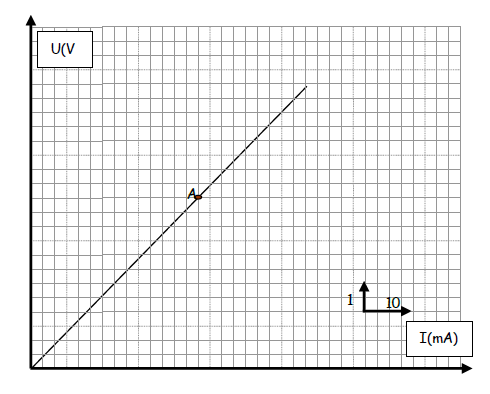
On considère la caractéristique intensité tension d'un dipôle

 

1) Représenter un schéma du montage qui nous a permis de tracer cette caractéristique

 

2) Préciser en justifiant la réponse, la nature du dipôle étudié, déterminer sa résistance

 

On réalise un circuit électrique simple avec une pile dont la tension entre ses bornes est $U=12\;V$ et un résistor de résistance $R=100\Omega$ qui supporte une intensité maximale de $100\;mA.$

 

1) Ne risque-t-on pas d'endommager $R\ ?$ Justifier.

 

2) Quelle résistance minimale $R'$ faut-il mettre en série avec $R$ dans le circuit pour pouvoir fermer sans dommage l'interrupteur.

 

3) On branche $R\ $ et $\ R''$ en parallèle, $R''$ inconnue, et les deux en série avec $R'$ minimale aux bornes du générateur.

 

a) Déterminer la valeur de $R''$ pour que l'intensité du courant soit égale à $0.12\;A$

 

b) Déterminer l'intensité du courant qui traverse $R'$ en déduire celui qui traverse $R.$

 

On fournit la caractéristique d'un conducteur ohmique

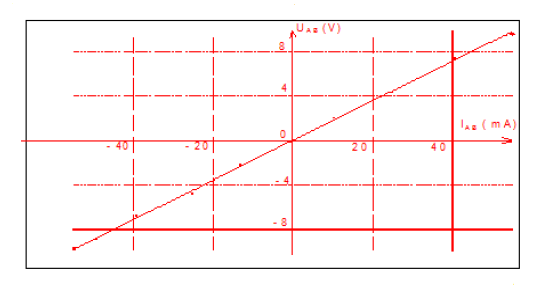
1) Expliquer pourquoi l'observation de ce graphe permet d'affirmer que le dipôle AB est un conducteur ohmique.

 

2) Faire le schéma conventionnel du dipôle AB en plaçant les deux points $A\ $ et $\ B$, la flèche tension $U_{_{AB}}$ et le courant $I.$

 

3) Calculer la résistance du conducteur ohmique à partir de sa caractéristique.

 

4)

4.1) Quelle est la tension aux bornes du conducteur ohmique lorsqu'il est traversé par un courant de $15\;mA\ ?$

 

4.2) Quelle est l'intensité du courant qui traverse le conducteur ohmique lorsqu'il est soumis à une tension de $4\;V\ ?$

 

5) Le professeur a conseillé à l'élève de ne pas alimenter le dipôle sous une tension supérieure à $10\;V.$

 

Quelle est l'intensité maximale que peut supporter le composant ?

 

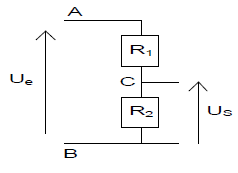
Un diviseur de tension est composé de deux conducteurs ohmiques $R_{1}\ $ et $\ R_{2}$ montés en série. 

 

Il est alimenté par une tension $U_{_{AB}}$ (tension d'entrée $U_{e}$) et la tension $U_{_{CB}}$ (tension de sortie $U_{s}$) peut être appliquée aux bornes d'un appareil dans lequel elle fera circuler un courant.

 

1) Le diviseur de tension est à vide. Aucun appareil n'est branché entre $C\ $ et $\ B.$

 

1.1) Exprimer en fonction de $U_{e}\;,\ R_{1}\ $ et $\ R_{2}$ l'intensité $I$ du courant qui circule dans le circuit.

 

1.2) En déduire l'expression de la tension de sortie $U_{s}$ en fonction de $U_{e}\;,\ R_{1}\ $ et $\ R_{2}.$

 

1.3) Applications numériques :

$U_{e}=6.0\;V\;,\ R_{1}=2.2\;k\Omega\ $ et $\ R_{2}=4.7\;k\Omega$

 

Calculer les valeurs de $I$ et de $U_{s}.$

 

2) Le diviseur de tension alimente maintenant un conducteur ohmique dont la résistance $R=1.0\;k\Omega$ (le diviseur de tension est dit en charge).

 

2.1) Représenter le schéma du circuit réalisé.

 

2.2) Déterminer la résistance équivalente $R_{e}$ à l'association des conducteurs ohmiques de résistances $R_{2}\ $ et $\ R.$

 

2.3) Déterminer la résistance équivalente $R'_{e}$ à l'ensemble du circuit $R_{1}\;,\ R_{2}\ $ et $\ R$, c'est à dire au dipôle $AB.$

 

2.4) En déduire les intensités des courants dans les conducteurs de résistances $R_{1}\;,\ R_{2}\ $ et $\ R.$

 

2.5) Montrer que la tension de sortie est alors $U'_{s}$ différente de $U_{s}$

 

Soient les deux dipôles résistors $R_{1}=10\Omega\ $ et $\ R_{2}=20\Omega.$

 

1) Dans le premier circuit ci-dessous, l'ampèremètre indique un courant d'intensité $I=0.2\;A$

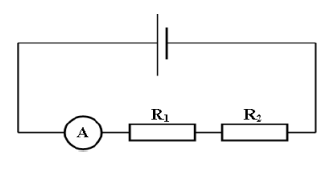
a) Le circuit est-il en série ou en dérivation ?

 

b) Représenter le branchement des voltmètres permettant la mesure des tensions $U_{1}$ aux bornes de $R_{1}$ et $U_{2}$ aux bornes de $R_{2}.$

 

c) Rappeler la loi d'Ohm relative à un résistor.

 

d) Calculer les tensions $U_{1}\ $ et $\ U_{2}.$

 

e) En déduire, en précisant la loi utilisée, la tension aux bornes du générateur.

 

f) Calculer la résistance équivalente à cette association de $R_{1}\ $ et $\ R_{2}$

 

2) On considère que la tension aux bornes du générateur reste constante. On réalise avec les mêmes dipôles le deuxième circuit suivant :

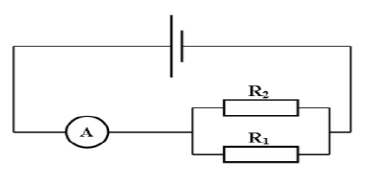
a) Les résistors dans ce deuxième circuit sont-ils associés en série ou en dérivation ?

 

En déduire $R'_{eq}$ la résistance équivalente à cette association de $R_{1}\ $ et $\ R_{2}$

 

b) Combien de voltmètres faut-il utiliser pour mesurer la tension $U'_{1}$ aux bornes de $R_{1}$ et $U'_{2}$ aux bornes de $R_{2}\ ?$

 

Préciser la valeur de chacune de ces deux tensions

 

c) Calculer l'intensité du courant $I_{1}$ traversant $R_{1}$

 

d) Calculer l'intensité du courant $I_{2}$ traversant $R_{2}$

 

e) En déduire l'intensité $I'$ du courant mesurée par l'ampèremètre en précisant la loi utilisée.

 

f) Calculer le rapport $\left(\dfrac{U_{\text{Générateur}}}{I'}\right)$ et le comparer avec la résistance $R'_{eq}$

 

3) Comparer les intensités du courant $I\ $ et $\ I'.$ 

 

En déduire une comparaison entre les intensités du courant débité par le même générateur dans un circuit en série et un circuit en dérivation comportant les mêmes dipôles

 

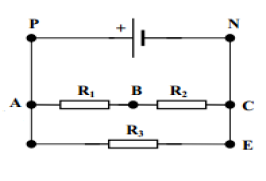
Un circuit électrique comporte un générateur de tension continue et trois conducteurs ohmiques de résistance $R_{1}\;,\ R_{2}\ $ et $\ R_{3}$ (voir schéma). On donne $R_{3}=220\Omega.$

 

1) Recopier le schéma ci-dessous, y placer le sens conventionnel du courant électrique

 

L'intensité mesurée dans la branche $PN$ vaut : $I=69.5\;mA$

2) Calculer le nombre d'électrons traversant une section de la branche $PN$ pendant une seconde.

 

3) Représenter les tensions positives aux bornes de chacun des dipôles. Justifier.

 

4) La tension électrique aux bornes du générateur est de $6.20\;V.$ Déterminer les intensités $I_{1}\ $ et $\ I_{2}$ des courants circulant dans les branches $ABC\ $ et $\ DE.$ Justifier

 

5) La tension électrique aux bornes du conducteur ohmique de résistance $R_{1}$ est de $4.13\;V$

 

Déterminer les résistances $R_{1}\ $ et $\ R_{2}$ des conducteurs ohmiques de la branche $ABC.$

 

Données : $e=1.6\;10^{-19}\;C$

 

On se propose de déterminer la caractéristique d'un dipôle inconnu $D$

 

1) Rappeler la définition de la caractéristique d'un dipôle. Quels sont les appareils de mesure nécessaires à sa détermination.

 

2) Représenter le schéma du montage électrique correspondant avec les appareils de mesure 

 

3) Les résultats des mesures sont regroupés dans le tableau suivant

 

$$\begin{array}{|l|c|c|c|c|c|c|c|c|}\hline U(V)&0&1&1.5&2&3.5&5&7&8\\ \hline I(mA)&0&2.1&3.2&4.2&7.4&10.0&14.9&17\\ \hline\end{array}$$

 

Tracer la représentation graphique $U=f(I)$ sur papier millimétré $(1\;cm$ pour $0.5\;V$ et $1\;cm$ pour $1\;mA).$

 

4) Qu'obtient-on comme courbe ? Qu'en déduit-on sur la nature du dipôle $D.$ 

 

Justifier en rappelant la loi appropriée.

 

5) Déterminer la valeur de la grandeur caractérisant le dipôle $D$

 

Si une diode Zener est parfois utilisée pour protéger un dispositif des variations de tension, il arrive qu'il faille protéger la diode Zener elle-même. 

 

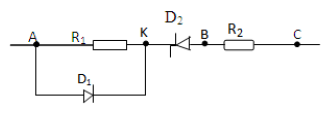
C'est le but du dispositif de la figure ci-dessous figure 2

 

Caractéristiques de la diode à jonction 

 

$D_{1}\ :\ I_{_{FM}}=1\;A\;;\ U_{s}\approx 0\;V\;;\ U_{_{RM}}=100\;V.$

 

Caractéristiques de la diode Zener

 

$D_{2}\ :\ I_{_{FM}}=100\;mA\;;\ U_{s}\approx 0\;V\;;\ U_{_{RZ}}=8\;V\;;\ I_{_{RM}}=60\;mA$

 

Les deux diodes sont considérées comme idéales. La tension $U_{_{AC}}$ appliquée aux bornes du circuit vaut $+12\ V$, soit $-12\;V$

 

1) La tension $U_{_{AC}}$ vaut $+12\;V.$ Quel est le rôle de $D_{1}\ ?$

 

Calculer la résistance $R_{2}$ minimale pour que la diode $D_{2}$ soit protégée. 

 

La diode $D_{1}$ est-elle alors protégée elle aussi ?

 

2) La tension $U_{_{AC}}$ vaut $-12\;V.$ Calculer la résistance $R_{1}$ pour que la diode $D_{2}$ soit protégée

On considère une $VDR$ que l'on a étudié en convention récepteur; les résultats sont regroupés dans le tableau ci-dessous

 

$$\begin{array}{|c|c|c|c|c|c|}\hline U(\text{en }V)&I(\text{en }A)&U(\text{en }V)&I(\text{en }A)&U(\text{en }V)&I(\text{en }A)\\ \hline0&0&1.4&0.47&2.8&1.12\\ \hline 0.2&0.06&1.6&0.55&3.0&1.23\\ \hline 0.4&0.12&1.8&0.63&3.4&1.16\\ \hline 0.6&0.18&2.0&0.72&3.8&1.71\\ \hline 0.8&0.25&2.2&0.81&4.2&2.03\\ \hline 1.0&0.32&2.4&0.91&4.6&2.47\\ \hline 1.2&0.39&2.6&1.01&5.0&3.51\\ \hline\end{array}$$

 

1) Tracer la caractéristique de la $VDR.$

 

On associe en série cette $VDR$ avec un générateur linéaire de f.é.m $E=4.5\;V$ et de résistance interne $r=3\Omega.$

 

2) Quelle relation existe-t-il entre l'intensité et la tension pour ce générateur ?

 

Tracer la caractéristique de ce générateur.

 

3) Déterminer graphiquement la valeur de l'intensité circulant dans le circuit ainsi que celles des tensions aux bornes de chacun des deux composants.

 

On associe maintenant le générateur précédent ainsi qu'un conducteur ohmique de résistance $R=0.87\Omega$ en parallèle avec la $VDR$ de telle sorte que l'on ait trois branches.

 

4) Déterminer la relation entre l'intensité et la tension pour les deux branches générateur – conducteur $R.$

 

5) Déterminer la valeur de la tension aux bornes de chacun des trois composants ainsi que celles des intensités du courant circulant dans chacune des trois branches

 

On considère le circuit suivant comportant les 5 résistors $R_{1}\;;\ R_{2}\;;\ R_{3}\;;\ R_{4}\ $ et $\ R_{5}$ :

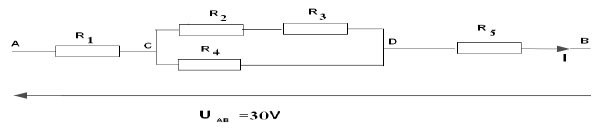
$R_{1}=R_{5}=25\Omega\;;\ R_{2}=R_{3}=R_{4}=50\Omega$

 

1) Déterminer la résistance équivalente du dipôle $CD.$

 

2) Déduire la résistance totale du dipôle $AB.$

 

3) Déterminer l'intensité du courant $I.$

 

4) Déduire les intensités $I_{2}\ $ et $\ I_{3}$ passant respectivement par $R_{4}\ $ et $\ (R_{2}+R_{3}).$

 

Soit le montage suivante :

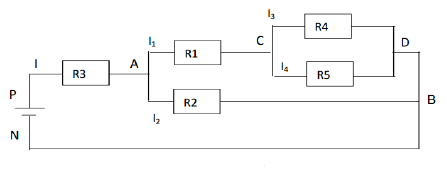
1) Représenter $U_{_{AB}}\;,\ U_{_{PN}}\;,\ U_{_{PA}}\;,\ U_{_{CA}}\;,\ U_{_{BN}}\ $ et $\ U_{_{CB}}.$

 

2) Que vaut $U_{_{BN}}\ ?$

 

3) Représenter le sens des courants.

 

4) Calculer $U_{_{PA}}.$

 

5) Calculer $I.$

 

6) Calculer $I_{2}.$

 

7) Calculer $R_{2}.$

 

8) Calculer $R_{1}.$

 

9) Calculer $U_{_{CB}}.$

 

10) Calculer $I_{3}.$

 

11) Calculer $I_{4}.$

 

12) Calculer $R_{5}.$

 

13) Calculer $R_{eq}$ la résistance équivalente aux 5 résistances en 4 étapes rédigées.

 

Données : $U_{_{PN}}=12\;V\;,\ U_{_{AB}}=8\;V\;,\ U_{_{AC}}=6\;V\;,\ R_{3}=200\Omega\;,\ R_{4}=200\Omega\;,\ I_{1}=15\;mA$

 

Une diode Zener utilisée en inverse est par les mesures suivantes :

$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|}\hline U(V)&0&2.0&5.0&5.2&5.5&5.6&5.7&5.8&5.82&5.86&5.90\\ \hline I(mA)&0&0&1.0&2.0&5.0&10&20&30&60&100&150\\ \hline\end{array}$$

 

Cette diode, toujours utilisée en inverse, est branchée avec un générateur de f.é.m $E=6\;V$, d'une résistance interne $r=1.8\Omega$ et avec un conducteur ohmique de résistance $R$

 

1) Tracer la caractéristique courant-tension de cette diode

 

2) Quelle doit la valeur de $R$ pour que la tension aux bornes de la diode soit $5.6\;V$

 

3) Que se passe-t-il en ce moment-là si la tension varie aux bornes de la pile ?

 

Dans quel de tension peut-on considérer que la diode Zener assure une régulation de la tension à ses bornes ?

Déterminer les valeurs correspondantes de $R$