Série d'exercices : Induction magnétique - Étude d'un dipôle RL - Ts
Classe:
Terminale
Exercice 1
I. Une bobine d'inductance $L$ et de résistance négligeable est reliée à un microampèremètre, comme l'indique la figure ci-dessous.
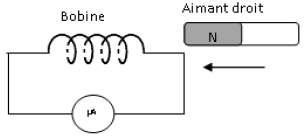
On rapproche l'aimant vers la bobine,
1) Quel est le phénomène observé
2) Indiquer le sens de circulation du courant induit dans la bobine
3) Préciser l'inducteur et l'induit
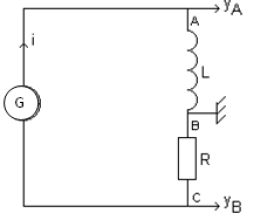
II. Avec la bobine précédente, on branche en série un résistor de résistance $R=10\,K\Omega$ et un générateur basse fréquence $(G.B.F$ à masse flottante$)$ qui délivre une tension triangulaire alternative.
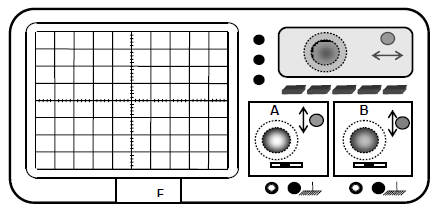
Sur l'écran d'un oscilloscope bicourbe, on visualise la tension $u_{AB}$ sur la voie $Y_{A}$ et la tension $u_{CB}$ sur la voie $Y_{B}$ (figure 4 page 3).
1) On note $i(t)$ l'intensité instantanée du courant qui traverse le circuit, son sens positif choisi est indiqué sur le schéma du montage.
a) Montrer, sans calcul, que la bobine est le siège d'un phénomène d'auto-induction
b) Montrer que la tension aux bornes de la bobine est $$u_{AB}=\dfrac{-L}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}$$
c) Justifier littéralement l'allure de la tension sur la voie $Y_{A}$
2) Les réglages de l'oscilloscope sont :
Sensibilité verticale de la voie $Y_{A}$ : $0.2V\cdot div^{-1}$
Sensibilité verticale de la voie $Y_{B}$ : $2V\cdot div^{-1}$
Sensibilité horizontale : $0.2\,ms\cdot div^{-1}$
A partir des oscillogrammes :
a) Calculer la période $T$ et la fréquence $N$ des tensions
b) Pendant la première demi-période, déterminer les expressions de $u_{AB}$ et de $u_{CB}$ en fonction du temps.
c) En déduire la valeur de l'inductance $L$ de la bobine.
Puis indiquer sa significationphysique.
Exercice 2
Dans une bobine $B_{1}$ qui est fermée sur un résistor de résistance $R$ on introduit une bobine $B_{2}$ qui est alimentée par un générateur de courant réglable.( voir figure)
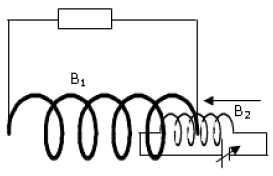
1 On introduit $B_{1}$ dans $B_{2}$ en gardant les deux axes de révolution des deux bobines confondus.
a) Représenter le champ magnétique créé par la bobine $B_{2}$
b) Énoncer la loi de Lenz.
Représenter le champ magnétique induit dans la bobine $B_{1}.$
En déduire le sens du courant induit.
c) Préciser l'inducteur et l'induit.
2) La bobine $B_{2}$ est fixée à l'intérieur de $B_{1}$, on diminue l'intensité du courant débitée par le générateur
a) Comment varie la valeur du champ magnétique créé par la bobine $B_{2}.$
b) Représenter le champ magnétique créé par $B_{2}$ et celui qui est induit dans $B_{1}.$
c) Préciser le sens du courant induit dans $B_{1}.$
3) On modifie les bornes du générateur et on répète l'expérience de la question 1, représenter le champ magnétique induit dans la bobine $B_{1}.$
Exercice 3
On réalise le montage série comportant une bobine d'inductance $L$ et de résistance négligeable, une résistance de valeur $R=10k\Omega$ ainsi qu'un générateur basse fréquence dont la masse n'est pas reliée à la terre(masse flottante).
1) Réaliser le schéma de principe du montage.
Ajouter les branchements à effectuer pour visualiser la tension aux bornes de la bobine sur la voie $A$ et la tension aux bornes de la résistance $R$ sur la voie $B.$
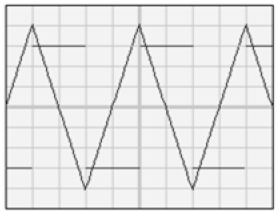
base de temps : $0.5\,ms/div$
sensibilité voie $A$ : $0.1V/div$
sensibilité voie $B$ : $2V/div$
2) L'une de ces tensions permet d'observer l'allure de $i(t).$
Laquelle ?
justifier la réponse.
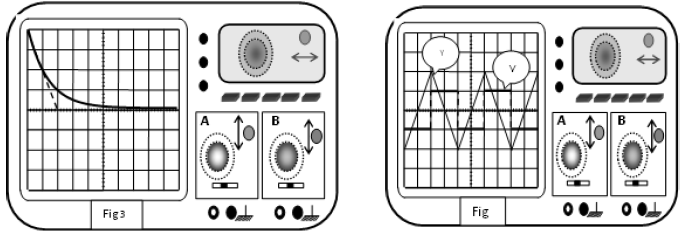
3) L'oscillogramme ci-après donne l'allure des différentes tensions observées.
Déterminer la période $T$ de l'intensité du courant.
4) Déterminer l'amplitude $I_{m}$ (valeur maximale atteinte) de l'intensité du courant.
5) On considère, sur l'oscillogramme précédent, une demi-période où la tension $u_{L}$ aux bornes de la bobine est positive.
a) Déterminer la valeur de la tension $u_{L}.$
b) Déterminer la valeur de la dérivée par rapport au temps de l'intensité du courant.
c) En déduire la valeur $L$ de l'inductance de la bobine.
Exercice 4
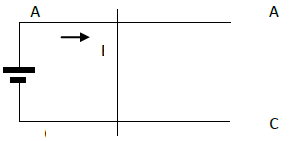
Deux rails conducteurs $(AA')$ et $(CC')$, parallèles et de résistances négligeables, séparés par une distance $L=25\,cm.$
Une tige $(MN)$ métallique de masse négligeable, perpendiculaire aux rails, peut glisser sans frottement dans une direction parallèle aux rails. (Voir figure)
La résistance de la longueur $L$ de la tige est $r=0.5\Omega.$
L'ensemble est placé dans un champ magnétique uniforme $\overrightarrow{B}$ d'intensité $B=1T.$
1) On branche entre les extrémités $A$ et $C$ des deux rails un générateur $G$ de courant continu, on remarque que la tige se met en mouvement en se dirigeant de $A$ vers $A'.$
Déterminer la direction et le sens du vecteur champ magnétique $\overrightarrow{B}.$
2) On élimine le générateur $G$ et on le remplace par un fil conducteur puis on déplace la tige $MN$ de sa position initiale $AC$ vers la droite sur les rails, à une vitesse $V=10\,m\cdot s^{-1}.$
a) Choisir sur le circuit un sens positif et tracer le vecteur surface $S.$
b) Déterminer l'expression du flux magnétique à travers le circuit pour une position quelconque de la tige $(MN)$ en fonction du temps.
Montrer que ce flux s'écrit sous la forme :
$\Phi=B\cdot L\cdot V\cdot t.$
2) a) Calculer la force électromotrice induite
b) Calculer l'intensité $i$ du courant induit
c) Déterminer le sens du courant induit.
b) Représenter $i$ sur le schéma
Exercice 5
Une spire plane de surface $s=2.5\,cm^{2}$ de résistance $r'=2\Omega$, placée à l'intérieur d'un solénoïde de longueur $l=40\,cm$, de rayon $R=5\,cm$, comportant $103$ spires et de résistance $r=2\Omega$ perpendiculairement à son axe $(\Delta).$
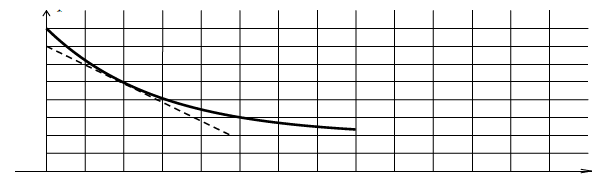
Le solénoïde est parcouru par un courant d'intensité $i(t)$ qui varie selon la courbe suivante :
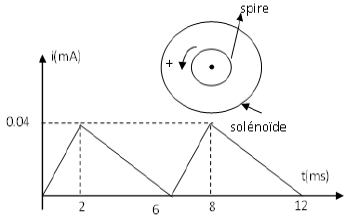
1) a) Établir l'expression de l'inductance $L$ du solénoïde.
Calculer sa valeur
b) Donner l'expression de $i(t)$ dans chaque intervalle de temps.
c) Quel est le phénomène qui se produit dans le solénoïde ?
Justifier la réponse.
d) Calculer la $f.e.m$ induite dans le solénoïde dans chacun des intervalles de temps $[0\;;\ 2\,ms]$ et $[2\;;\ 6\,ms].$
e) Représenter cette $f.e.m$ au cours du temps.
2) Représenter, en respectant le sens positif choisi, dans chacun des intervalles $[0\;;\ 2\,ms]$ et $[2\;;\ 6\,ms]$ respectivement sur la spire et sur le solénoïde le sens du courant induit et le sens du courant principal.
3) Calculer aux instants $t_{1}=2\,ms$ ;
$t_{2}=4\,ms$ et $t_{3}=6\,ms$ :
a) La tension aux bornes du solénoïde.
b) L'énergie magnétique emmagasinée par le solénoïde.
Exercice 6
On réalise le montage de la figure 1 où $R=10\Omega$, $E=9V$, $L$ et $r$ sont inconnues.
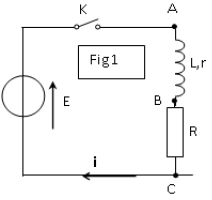
I. à l'origine du temps, on ferme l'interrupteur $K.$
Un oscilloscope à mémoire permet d'obtenir les chronogrammes de la figure 2.
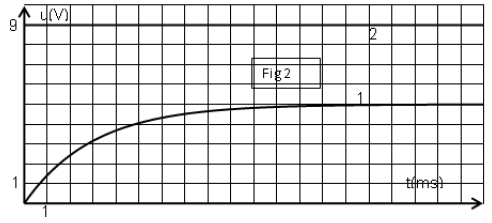
1) Reproduire le schéma du circuit en indiquant les branchements nécessaires qui permettent d'obtenir le chronogramme $1$ sur la voie $Y_{1}$ et le chronogramme $2$ sur la voie $Y_{2}.$
2) Interpréter la réponse du dipôle $RL$ à l'échelon de tension.
II.
1) Montrer que l'équation différentielle régissant les variations de la tension aux bornes du résistor $u_{R}(t)$ s'écrit sous la forme $$L\dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+(R+r)u_{R}=RE.$$
2) Sachant que la solution de cette équation différentielle est de la forme $u_{R}(t)=A(1-\mathrm{e^{-\alpha\,t}}).$
Montrer que $A=\dfrac{RE}{R+r}$ et $\alpha=\dfrac{R+r}{L}$
3) a) En régime permanent, déterminer graphiquement
$-\ $ l'intensité du courant $I_{p}.$
$-\ $ la tension $u_{B}$ aux bornes de la bobine.
b) en déduire que la résistance de la bobine est $r=8\Omega.$
c) Déterminer graphiquement la valeur de la constante de temps $\tau.$
Déduire la valeur de l'inductance $L$ de la bobine.
Exercice 7
On alimente un dipôle $"$bobine - résistance $R"$ par un générateur basse fréquence en série avec un dipôle ohmique de protection.
Aucune des bornes de sortie du générateur n'est reliée à la Terre.
La mesure de la résistance de la bobine donne $r=15\Omega$ et $R$ est une résistance variable.
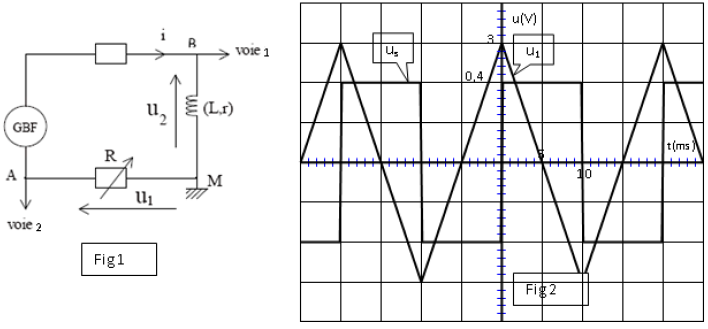
L'oscilloscope est branché comme indiqué sur le schéma (fig 1).
La touche $ADD$ de l'oscilloscope permet d'observer la somme $u_{S}$ des tensions des deux voies $1$ et $2$, $u_{S}=u_{1}+u_{2}.$
Sur la figure 2, on a reproduit avec la même origine des temps les courbes $u_{1}(t)$ et $u_{S}(t).$
1) Exprimer en fonction de $i$, $r$, $R$ et $L$ les tensions suivantes : $u_{1}$, $u_{2}$, $u_{S}(t).$
2) L'oscillogramme ci-dessus a été obtenu en ajustant $R$ à la valeur de $r.$
Montrer que dans ce cas $u_{S}=-\dfrac{L\mathrm{d}u_{1}}{r\mathrm{d}t}.$
3) En exploitant les chronogrammes de la figure 2, déterminer $L.$
Exercice 8
Un dipôle est constitué de l'association en série d'une bobine présentant une inductance $L$ et une résistance $R_{L}$ avec un conducteur ohmique de résistance $R=40W.$
Ce dipôle est alimenté par un générateur de tension de $f.é.m.$
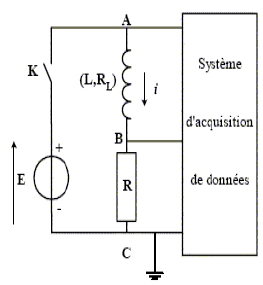
$E$ à travers un interrupteur $K.$
Il est parcouru par un courant $i.$
Les bornes $A$, $B$, et $C$ sont reliées aux entrées d'une carte d'acquisition permettant d'enregistrer l'évolution des tensions.
A l'instant $t=0$, on ferme l'interrupteur $K$, l'enregistrement génère les courbes $1$ et $2.$
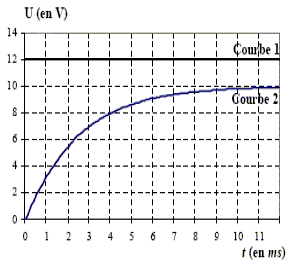
1) Quelle tension est représentée par la courbe 1 ?
2) Quelle tension est représentée par la courbe 2 ?

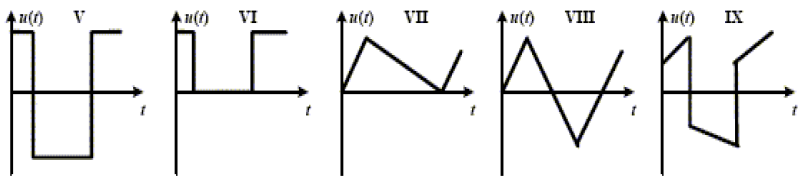
3) Quelle sera l'allure de la courbe de variation du courant $i$ choisie parmi les quatre courbes ci-dessous ?
4) Tracer l'allure de la courbe de variation de la tension $u_{AB}.$
5) Donner la valeur $E$ et l'intensité maximale $I_{max}$ atteinte par $i.$
6) Donner l'équation différentielle définissant $i.$
Cette équation sera présentée sous la forme d'une égalité où la $f.é.m.$
$E$ sera le seul terme du deuxième membre.
En déduire les valeurs de $L$ et $R_{L}.$
On remplace maintenant le générateur de tension par un générateur de courant délivrant un courant en dents de scie (courbe 3).
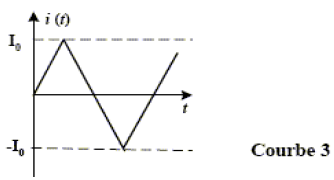
On considérera ici que la résistance $R_{L}$ de la bobine est nulle.
7) Quelle sera, parmi les cinq courbes ci-dessous, l'allure de la courbe de variation de la tension $u_{AB}$ et de la courbe de variation de la tension $u_{BC}.$
Exercice 9
On réalise un circuit électrique $AM$ comportant en série un conducteur ohmique de résistance $R=50\Omega$, une bobine $(B_{1})$ d'inductance $L$ et de résistance supposée nulle et un interrupteur $K.$
Le circuit $AM$ est alimenté par un générateur de tension de force électromotrice $(f.e.m)$ E (fig 1).
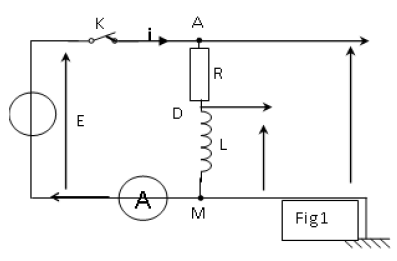
Un système d'acquisition adéquat permet de suivre l'évolution au cours du temps des tensions $u_{AM}$ et $u_{DM}.$
A l'instant $t=0s$, on ferme l'interrupteur $K.$
Les courbes traduisant les variations de $u_{AM}(t)$ et $u_{DM}(t)$ sont celles de la figure 2
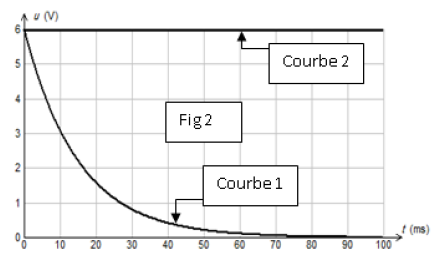
1) a) Montrer que la courbe 1 correspond à $u_{DM}(t).$
b) Donner la valeur de la $f.e.m$ du générateur.
2) a) A l'instant $t_{1}=10\,ms$, déterminer graphiquement la valeur de la tension $u_{B1}$ aux bornes de la bobine $(B_{1})$ et déduire la valeur de la tension $u_{R}$ aux bornes du conducteur ohmique.
b) A l'instant $t_{2}=100\,ms$, montrer que l'intensité du courant électrique qui s'établit dans le circuit électrique est $I_{0}=0.12\,A$
3) a) Déterminer graphiquement la valeur de la constante de temps $\tau$ du dipôle $RL.$
b) Sachant que $\tau=L/R$, déterminer la valeur de l'inductance $L$ de la bobine $(B_{1})$
c) Calculer l'énergie emmagasinée dans la bobine en régime permanent
4) On remplace la bobine $(B_{1})$ par une bobine $(B_{2})$ de même inductance $L$ mais de résistance $r$ non nulle.
Les courbes traduisant les variations de $u_{AM}(t)$ et $u_{DM}(t)$ sont celles de la figure 3.
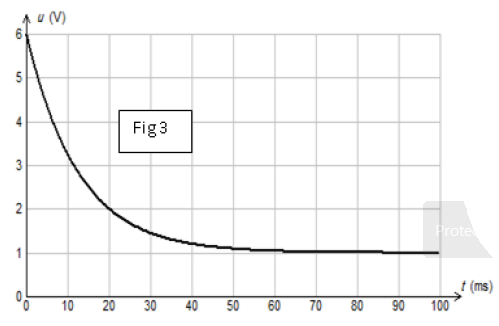
a) Montrer qu'en régime permanent, la tension aux bornes de la bobine $(B_{2})$ est donnée par la relation $u_{B_{2}}=\dfrac{r\,E}{R+r}$
b) Déduire la valeur de la résistance $r$
Exercice 10
On se propose d'étudier l'établissement du courant dans un dipôle série comportant une bobine d'inductance $L$ et une résistance $r$ et un conducteur ohmique de résistance $R_{0}=30\Omega$ lorsque celui-ci est soumis à un échelon de tension de valeur $E$ délivrée par un générateur de tension idéal.
Un oscilloscope à mémoire, est branché comme l'indique la figure 1, permet d'enregistrer au cours du temps les valeurs des tensions.
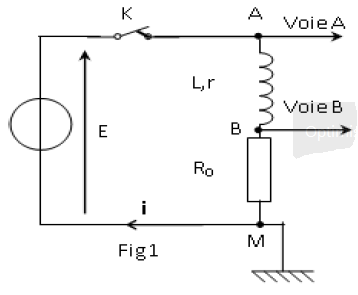
1) A l'instant $t=0$, on ferme l'interrupteur $K$, et on procède à l'enregistrement.
On obtient les courbes $y_{1}=f(t)$ et $y_{2}=g(t)$ (figure 2).
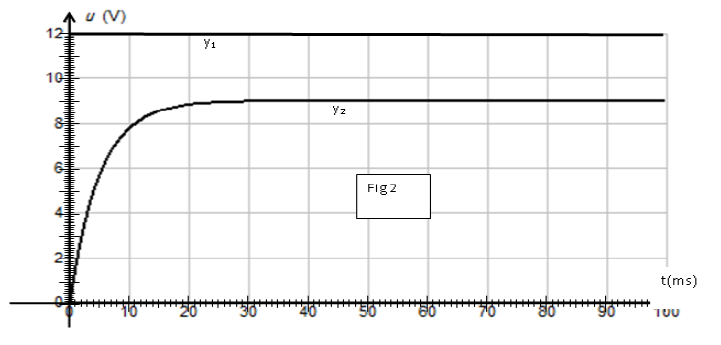
a) Quelles sont les grandeurs électriques observées sur les voies $A$ et $B$ ?
Identifier $y_{1}$ et $y_{2}.$
Justifier la réponse.
b) Quelle est la courbe qui permet de déduire la variation de l'intensité de courant $i$ au cours du temps ?
Expliquer brièvement le comportement électrique de la bobine.
c) Prélever du graphe la valeur de la force électromotrice du générateur.
2) Lorsque le régime permanent est établi, l'intensité $i$ prend la valeur $I_{p}$, tandis que $y_{2}$ prend la valeur $Y_{p}$
a) Donner, dans ces conditions, les expressions littérales des tensions $u_{AM}$, $u_{AB}$ et $u_{BM}.$
Montrer, en utilisant les courbes de la figure 2, que la bobine a une résistance $r$ non nulle.

Commentaires
Mamadou saliou barry (non vérifié)
jeu, 04/16/2020 - 02:02
Permalien
Suivre les cours et exo
Anonyme (non vérifié)
ven, 07/17/2020 - 08:54
Permalien
Svp aidez moi à avoir la
Maguette (non vérifié)
dim, 06/06/2021 - 19:44
Permalien
Je veux la correction de cette série
Anonyme (non vérifié)
ven, 12/08/2023 - 10:47
Permalien
Correction
Anonyme (non vérifié)
dim, 05/08/2022 - 18:05
Permalien
pdf
Bineta paye (non vérifié)
dim, 06/09/2024 - 22:07
Permalien
Pour mes études
Brahim TCHOU (non vérifié)
lun, 01/20/2025 - 11:01
Permalien
PHYSIQUE
Ajouter un commentaire