Série d'exercices : Interférences lumineuses - Ts
Classe:
Terminale
Exercice 1
Deux fentes $F_{1}$ et $F_{2}$ distantes de $a=2mm$ émettent de la lumière provenant d'une même fente $F$ Elles produisent un système d'interférences lumineuses sur un écran placé à la distance $D=2m$ des fentes.
La lumière de la source $F$ contient deux radiations monochromatiques, de longueur d'onde $\gamma_{1}=0.60\mu m$ et $\gamma_{2}=0.48\mu m.$
L'interfrange $i$ (distance séparant les milieux de deux franges sombres ou de deux brillantes consécutive) est lié à $\gamma$ par la relation $i=\gamma\dfrac{D}{a}$
1) Représenter à l'échelle $5$, sur une largeur de $15cm$ :
a) la figure d'interférences obtenue avec la radiation de longueur d'onde $\gamma_{1}$
b) la figure d'interférences obtenue avec la radiation de longueur d'onde $\gamma_{2}$
c) la figure d'interférences obtenue avec la lumière émise par la source $F$
2) Qu'observerait-on si la source Fémettait de la lumière blanche
Exercice 2
A l'aide d'un dispositif interférentiel, on crée deux sources lumineuses $S_{1}$ et $S_{2}$ synchrones et cohérentes distantes de $a.$
Quand le dispositif est éclairé par une source de lumière monochromatique de longueur d'onde $\gamma=0.6\mu m$, on observe des franges d'interférence sur l'écran $E$ placé à $D=2.5m$ de $S_{1}$ et $S_{2}$
1) Établir l'expression de la différence de marche au point $M$ de l'écran
2) Déterminer la distance entre les deux sources pour que la distance entre les milieux de la $6^{e}$ et $9^{e}$ frange brillante située de part et d'autre de la frange centrale numérotée $0$ soit égale à $1.5cm$
3) Déterminer la nature de la frange en un point $P$ de $E$ distant de $2.5mm$ de la frange centrale
Exercice 3
Deux fentes $F_{1}$ et $F_{2}$ sont éclairées par une fente source en lumière monochromatique rouge de longueur d'onde $\gamma=0.64\mu m$ et se comportent comme deux sources synchrones et en phase.
La figure d'interférence est observée sur un écran.
On considère un point $M$ sur un écran situé à la distance $d_{1}$ de $F_{1}$ et $d_{2}$ de $F_{2}$ (schéma)
1) Les vibrations lumineuses issues des fentes $F_{1}$ et $F_{2}$ sont-elles en phase ?
(Justifier les réponses)
2) La vibration lumineuse émise par la fente $F_{1}$ arrive en $M$ avec un certain retard.
Exprimer ce retard en fonction de $d_{1}$ et de la vitesse $c$ de la lumière dans l'air
3) Même question pour la vibration lumineuse issue de la fente $F_{2}$
4) En déduire à quelles conditions le point $M$ sera sur frange brillante ; sur une frange sombre $5.$
Que peut-on dire des points $M$ suivants :
$-\ $ $M$ est tel que $d_{2}-d_{1}=0$
$-\ $ $M$ est tel que $d_{2}-d_{1}=3.20\mu m$
$-\ $ $M$ est tel que $d_{2}-d_{1}=2.24\mu m$
Exercice 4
La lumière serait de nature contradictoire.
Si une théorie permet d'expliquer de nombreux phénomènes, elle peut s'avérer insuffisante pour en comprendre d'autres.
Le but de cet exercice est de montrer que, selon l'expérience réalisée, un des aspects du comportement de la lumière.
A cet effet on réalise le dispositif ci-dessous :
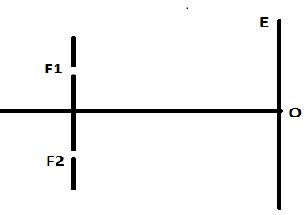
1) Dispositif expérimental
$(S)$ est une source de lumière qui éclaire deux fentes fines, verticales distantes de $a=1.5mm.$
La source $(S)$ est équidistante des deux fentes.
$(E)$ est un écran opaque vertical placé à une distance $D=2m$ du plan des fentes.
a) Quel phénomène se produit à la sortie de chaque fente ?
Quel aspect de la lumière permet-il de mettre en évidence ?
b) Justifier l'utilisation d'une source unique pour éclairer les deux dentes.
c) Reproduire le schéma et représenter la marche des faisceaux lumineux issus des fentes $F_{1}$ et $F_{2}.$
Hachurer le champ où l'on peut observer le phénomène d'interférence.
2) La source $(S)$ émet une lumière monochromatique de longueur d'onde $\gamma.$
a) Qu'observe-t-on sur l'écran ?
Préciser la direction des franges et la nature de la frange centrale qui se forme en $O.$
b) Pour déterminer la longueur d'onde $\gamma$, on compte $5$ franges brillantes de part et d'autres de la frange centrale occupant ensemble une largeur $l=8mm.$
En déduire la valeur de $\gamma.$
3) La source précédente $(S)$ est remplacée par une source $(S')$ qui émet simultanément deux radiations monochromatiques de longueur d'onde $\gamma_{1}=0.60\mu m$, et $\gamma_{2}=0.54\mu m.$
Il se produit une superposition des systèmes de franges formées par les deux radiations.
A quelle distance $x$ du point $O$ se produit la première coïncidence de franges brillantes ?
Exercice 5
Un pinceau de lumière monochromatique émis par un laser hélium-néon éclaire deux fentes parallèles séparées par une distance $a=05mm.$
Un écran est placé perpendiculairement au pinceau lumineux à une distance $D2m$ du plan des fentes.
Dessiner le dispositif expérimental.
1) Interpréter la formation des franges brillantes et obscures.
2) Définir et calculer la différence de marche aux $2$ fentes d'un point $M$ de l'écran, pour en déduire la position des franges brillantes et obscures
3) Préciser la nature de la frange centrale appartenant au plan médiateur des $2$ fentes.
4) Définir et calculer l'interfrange.
Quelle est l'influence des différents paramètres sur l'interfrange ?
Comment doit-on modifier la distance entre les $2$ fentes pour obtenir des franges plus espacées ?
5) Calculer la longueur d'onde et la fréquence de la lumière émise par le laser, sachant que $6$ franges sont espacées de $12.7mm.$
6) Est-ce que la longueur d'onde ou la fréquence change (ou aucune des deux), si le rayon lumineux se propage dans le verre ?
Calculer les nouvelles valeurs.
$($On sait que dans le verre la célérité de la lumière vaut $200000km/s.)$
Exercice 6
Une lumière monochromatique, issue d'une fente $F$, tombe sur un écran $E$ percé de deux fentes $F_{1}$ et $F_{2}$ parallèle à $F.$
Un dispositif spécial permet de faire varier la distance entre les fentes $F_{1}$ et $F_{2}$ $(F_{1}F_{2}=a)$ qui reste toute fois située à égale distance de $F.$
1) On dispose un écran $K$, parallèle à $E$ et à une distance $d$ de celui-ci.
Qu'observe-t-on sur l'écran $K$
2) La longueur d'onde de la lumière monochromatique est $\gamma.$
On mesure dans le plan $K$ l'intervalle $L$ séparant $N$ franges brillantes consécutives.
Établir la formule donnant $a$ en fonction de $\gamma$, $N$, $d$ et $L$ (On supposera établie la formule de l'interfrange)
Calculer $a$ lorsque $\gamma=0.55\mu m$, $L=7.2mm$, $N=7$ et $d=1.20m$
3) On augmente l'intervalle $a=F_{1}F_{2}$
Qu'en résulte-il sur le phénomène observé sur l'écran ?
D'autre part on remarque que pour un interfrange inférieur à $0.2mm$, l'observation du phénomène devient très difficile à l'œil nu.
Quelle sera la valeur limite $a'$ de la distance $F_{1}F_{2}$ séparant les deux fentes ?
4) Combien observe-t-on de franges brillantes sur l'intervalle $L=7.2mm$ de l'écran $K$ quand $a=a'$ ?
La mesure de l'intervalle est faite à partir d'une frange brillante
Exercice 7
1) Soit la distance de deux fentes fines et parallèles $F$ et $F'$ dans l'expérience de Young.
On éclaire $F$ et $F'$ par une fente lumineuse parallèle aux précédentes et à égale distance de chacune d'elle.
soit $\gamma$ la longueur d'onde dans le vide de la lumière monochromatique employée.
On observe dans l'air des franges d'interférences sur un écran $(P)$ parallèle au plan des deux fentes et situé à une distance $d$ de ses fentes.
Soit la largeur de $N$ interfranges consécutifs (on prendra comme plan de figure un plan perpendiculaire au plan $(FF')$
1.1 Établir la relation donnant $\gamma$ en fonction de $a$, $d$, $i$ et $N.$
AN :
$a=2.00\,mm$ ; $1=4.00\,mm$ ; $N=12$ et $d=1.00m.$
Calculer $\gamma$
1.2 Quelle serait la nouvelle longueur $l$ du même nombre $N$ d'interfranges si tout le dispositif était plongé dans un milieu d'indice par rapport à l'air
A.N :
$n_{o}=1.30$
1.3 Le système étant placé dans l'air, on recouvre la fente $F$ du côté de l'écran par un verre à faces parallèles d'épaisseur $e$ et d'indice $n=1.52.$
Qu'observe-t-on sur l'écran.
Expliquer le phénomène.
Calculer $e$ si le déplacement de la frange centre est $X=4.40mm$
1.4 On place sur $F$ une autre lame d'épaisseur $e'$ et d'indice $n'$ ; le système de franges obtenu est alors identique à celui réalité avant la mise en place des deux lames.
Donner en fonction de $e$, $n$ et $n'$ l'expression de $e'$
Calculer $e'$ si $n'=1.402.$
Le dispositif est celui de la question 1., mais la source émet deux radiation : $\gamma=0.550\mu m$ et $\gamma=0.650\mu m.$
On observe simultanément les deux franges.
Déterminer dans le plan $(p)$, la plus petite distance par rapport à la frange centrale ou les milieux de deux franges brillantes correspondant aux deux radiation coïncident.
Exercice 8
La source $F$ n'est plus monochromatique, mais des filtres permettent d'obtenir des radiations monochromatiques différentes (voir figure).
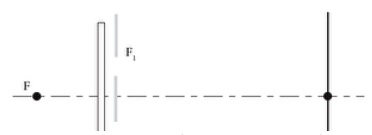
Pour chaque radiation, on mesure la longueur d'onde correspondant à $6$ interfranges $i$ $(i$ est la distance séparant le milieu de deux franges brillantes consécutives ou de deux franges sombres consécutives$)$ (voir figure).
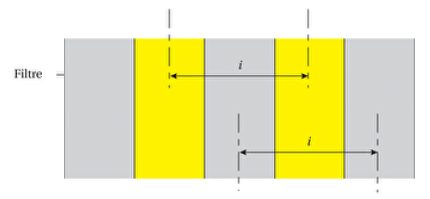
1) Pourquoi mesure-t-on la distance correspondant à $6$ interfranges plutôt que celle mesurant $1$ interfrange ?
2) On a obtenu les résultats suivants.
Compléter le tableau.
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Couleur}& & & & &\\ \hline 6i&14.1&15.6&17.4&18.3&19.5\\ \hline \gamma(\mu m)&0.47&0.52&0.58&0.61&00.65\\ \hline \end{array}$$
3) Tracer la courbe représentative de la fonction $i=f(\gamma).$
4) La relation $i=\gamma\dfrac{D}{a}$ est-elle en accord avec la courbe obtenue précédemment ?
5) Comment faudrait-il modifier le dispositif expérimental pour obtenir des mesures avec une plus grande précision ?
6) Quelle serait la valeur de l'interfrange obtenu avec une radiation de longueur d'onde $0.50\mu m$ ?
7) On dispose d'une source monochromatique de longueur d'onde inconnue.
Comment feriez vous expérimentalement pour la déterminer.
Exercice 9
On réalise une expérience d'interférences lumineuses avec le dispositif d'Young, en utilisant une lumière monochromatique de longueur d'onde $\gamma\,l=0.52\mu m.$
La fente-source $F$ éclaire deux fentes fines identiques $F_{1}$ et $F_{2}$ situées dans un plan vertical et distantes de $F_{1}F_{2}=a=2mm.$
Un écran d'observation $(E)$ est placé à $150cm$ du plan contenant $F_{1}$ et $F_{2}$ et parallèlement à celui-ci.
1) a) Décrire et expliquer le phénomène observé sur l'écran $(E).$
b) Quelle conclusion peut-on en tirer quant à la nature de la lumière ?
2) Définir et calculer l'interfrange $i.$
3) La frange centrale brillante est d'ordre zéro.
Calculer la distance séparant la troisième frange brillante à gauche de la frange centrale et la deuxième frange noire à droite de cette frange centrale.
La fente-source $F$ émet maintenant une radiation monochromatique de longueur d'onde $\gamma_{2}=0.65\mu m.$
4) A quelle distance de cette fente-source $F$ doit-on placer l'écran d'observation $(E)$ pour que l'interfrange $i'$ obtenu avec ce dispositif soit égal à l'interfrange $i$ de la question 2 ?
La distance entre la fente-source $F$ et le plan contenant $F_{1}$ et $F_{2}$ est égale à $50cm.$
5) La fente-source $F$ émet simultanément les deux radiations de longueurs d'onde $\gamma_{1}=0.52\mu m$ et $\gamma_{2}=0.65\mu m.$
On remet l'écran $(E)$ à la position où il est distant de $150cm$ du plan contenant $\gamma_{2}=0.65\mu m.$
On remet l'écran $(E)$ à la position où il est distant de $150cm$ du plan contenant $F_{1}$ et $F_{2}.$
6) A quelle distance de la frange centrale aura lieu la première coïncidence des franges brillantes des deux systèmes de franges obtenus.
Exercice 10
Le dispositif des fontes d'YOUNG schématisé sur la figure 1 permet de réaliser une expérience de mise en évidence d'interférences lumineuses.
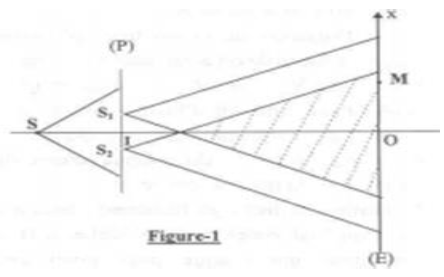
La source $(S)$ émet une lumière monochromatique de longueur d'onde $\gamma=0.6\cdot10^{-6}m$
$(P)$ est un plan opaque comportant deux fentes fines $S_{1}$ et $S_{2}$ distantes de $a=1\,mm$ et assimilables à deux sources ponctuelles monochromatique symétriques par rapport à un point $I$ milieu de $S_{1}S_{2}.$
Un écran $(E)$ est disposé parallèlement à $(P)$ et à une distance $D=2\,m$ de celui-ci.
On observe des interférences lumineuses dans la représenté hachurée sur le schéma où les deux faisceaux issus de $S_{1}$ et $S_{2}$ couvrent une partie commune.
L'intersection de cette zone hachurée avec l'écran $(E)$ est un ensemble de franges brillantes équidistantes ayant la couleur de lumière monochromatique.
Deux franges brillantes successives sont séparées par une frange sombre, et la frange centrale en $O$ est brillante.
Un point $M$ du champ d'interférence est repéré par son abscisse $x=OM$
Lorsque $M$ appartient à une frange brillante, il vérifie la relation $MS_{2}-MS_{1}=k\gamma$ $($avec $k$ entier$).$
Par contre s'il appartient à une frange sombre il vérifie la relation $MS_{2}-MS_{1}=(2k+1)\dfrac{\gamma}{2}$ $($avec $k$ entier$).$
1) a) Montrer que la différence de marche a pour expression $(MS_{2}-MS_{1})=\dfrac{ax}{D}$
b) En déduire l'expression de l'abscisse $x$ d'un point $M$ de l'écran en fonction de $\gamma$, $D$ et $a$ :
$-\ $ Lorsqu'il appartient à une frange brillante
$-\ $ Lorsqu'il appartient à une frange sombre.
2) a) Déterminer l'expression de l'interfrange $i$ en fonction de $\gamma$, $D$ et $a.$
Calculer $i.$
b) Préciser, en le justifiant, la nature (brillante ou sombre) de la frange d'abscisse $x=-4.2mm.$
3) On apporte les changements suivants au dispositif expérimental de la figure 1 :
$-\ $ On supprime la source $(S)$ et le plan opaque $(P)$
$-\ $ à l'emplacement des deux sources secondaires $S_{1}$ et $S_{2}$ on dispose de deux sources $S'_{1}$ et $S'_{2}$ totalement indépendantes, émettant chacune la lumière monochromatique de longueur d'onde $l=0.6\cdot10^{-6}m.$ (figure 2)
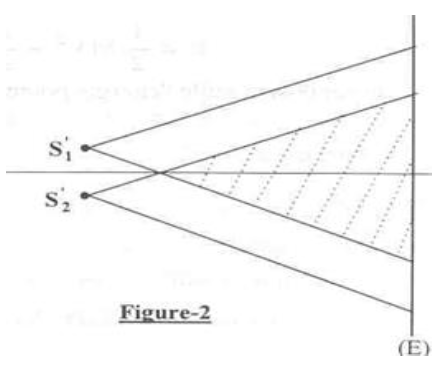
On n'observe d'interférences lumineuses.
Expliquer pourquoi ?
4) Citer un dispositif, autre que les fentes d'YOUNG, permettant de réaliser une expérience de mise en évidence d'interférences lumineuses :
$-\ $ on tracera la marche des rayons lumineux
$-\ $ et on hachurera la zone où les deux faisceaux lumineux, issus des deux sources secondaires, couvrent une partie commune correspondant aux interférences lumineuse.

Commentaires
Fatou (non vérifié)
mer, 04/29/2020 - 14:48
Permalien
Exercice
bambara eric (non vérifié)
mar, 01/12/2021 - 12:19
Permalien
se documenter
bambara (non vérifié)
mar, 03/02/2021 - 09:41
Permalien
se documenter
Danaya (non vérifié)
mer, 08/26/2020 - 22:53
Permalien
Devenir ingenie
Edward sounkéné (non vérifié)
mer, 02/02/2022 - 07:27
Permalien
Recherche d'exercice
sadja (non vérifié)
mar, 06/07/2022 - 10:36
Permalien
solution de l'exercice
Condé (non vérifié)
sam, 05/27/2023 - 11:06
Permalien
Étudié
Condé (non vérifié)
sam, 05/27/2023 - 11:06
Permalien
Étudié
Ajouter un commentaire