Série d'exercices : Le poids - La masse - Relation entre poids et masse - 2nd S
Classe:
Seconde
Exercice 1
Un solide en aluminium de masse $m=30\;g$ et de volume $V=12\;cm^{3}.$
1) Calculer sa masse volumique $\rho$ en $g.cm^{-3}$ puis en $kg.m^{-3}$.
2) Calculer sa densité d par rapport à l'eau (on donne : $\rho_{eau}=1\;g.cm^{-3}$)
3) Sachant que la masse volumique de l'aluminium est $\rho_{Al}=2.7\;g.cm^{-3}$ écris "Vrai" ou "faux" devant chacune des affirmations suivantes :
a) Si le solide est plein alors il est en aluminium pur.
b) Si le solide est plein alors il est un alliage d'aluminium et d'un autre métal de masse volumique inférieure à $2.7\;g.cm^{-3}.$
c) Si le solide est en aluminium pur alors il est plein.
4) Sachant que le solide est en aluminium pur.
a) Montre que 'il est creux.
b) Détermine le volume $V_{c}$ de la cavité située à l'intérieure du solide
Exercice 2
Un corps solide $(S)$ de masse $m=75\;g$ a la forme d'un cube d'arête $a=5\;cm.$
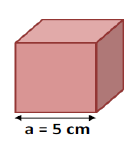
1) Calculer le volume du solide $(S).$
2) Calculer la masse volumique du solide $(S)$ en $g.cm^{-3}$ et en $kg.m^{-3}.$
3) Quelle est la nature du solide $(S)$ en utilisant le tableau ci-dessous
$$\begin{array}{|c|c|c|c|c|}\hline\text{Corps}&\text{Aluminium}&\text{Cuivre}&\text{Liège}&\text{Bois}\\\hline\rho\,(kg.m^{-3})&2700&8900&240&600\\\hline\end{array}$$
4) Calculer la densité du solide $(S)$ par rapport a l'eau.
On donne : la masse volumique de l'eau $\rho_{eau}=1000\;kg.m^{-3}.$
5) On introduit le solide $(S)$ dans un récipient contenant de l'eau. Dire en justifiant la réponse si le solide $(S)$ coule ou flotte "se situer au font du récipient ou a la surface de l'eau".
Exercice 3
I. Un commerçant désire acheter de l'huile pure, il pratique la démarche expérimentale suivante en utilisant un échantillon d'huile comme le montre la figure suivante :
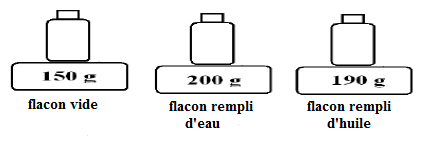
1) A partir des pesées précédentes, calculer :
a) La masse $m$ d'eau
b) La masse $m'$ d'huile
c) On donne $\rho_{eau}=1\;g.cm^{-3}$
Déduire le volume d'eau $V$ contenu dans le flacon en $cm^{3}$ puis en $l.$
2) a) Déterminer la densité $d'$ de l'huile par rapport à l'eau.
b) Sachant que la masse volumique $\rho_{huile}=0.92\;g.cm^{-3}$ Conclure
II. On dispose d'un bêcher de capacité $100\;ml$ et d'un corps $C$ de forme cubique de $4\;cm$ de côté
1) Calculer le volume $V$ du corps $C.$
2) a) Peut-on mesurer le volume du corps $C$ en l'introduisant dans un bêcher contenant $50\;ml$ d'eau ?
Pourquoi ?
3) Calculer le volume d'eau déversée $V_{D}$ lorsqu'on met le corps $C$ dans le bêcher
Exercice 4
Soient deux liquides $L_{1}\ $ et $\ L_{2}.$ On réalise les expériences schématisées ci-dessous.
1.a) Déterminer la masse $m_{1}$ du liquide $L_{1}.$
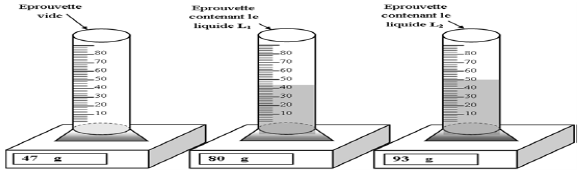
b) Calculer la masse volumique $\rho_{1}$ du liquide $L_{1}$ en $g.cm^{-3}$ puis en $kg.m^{-3}$
c) Déduire la densité $d_{1}$ du liquide $L_{1}$ par rapport à l'eau.
2.a) Déterminer la masse $m_{2}$ du liquide $L_{2}.$
b) Calculer la masse volumique $\rho_{2}$ du liquide $L_{2}$ en $g.cm^{-3}$ puis en $kg.m^{-3}$
c) Déduire la densité $d_{2}$ du liquide $L_{2}$ par rapport à l'eau.
3) Lequel de ces deux liquides est le plus dense ? Justifier la réponse.
4) On mélange ces deux liquides.
a) Quel est la nature du mélange obtenu.
b) Calculer la masse volumique du mélange.
Exercice 5
Le poids d'un corps est une grandeur physique exprimée en Newton $(N)$ qui indique la force de pesanteur d'origine gravitationnelle exercée par la Terre sur un corps massique.
Le poids se mesure avec un dynamomètre, instrument de mesure muni d'un ressort dont l'allongement correspond au poids du corps qui y est suspendu. On réalise les mesures suivantes :
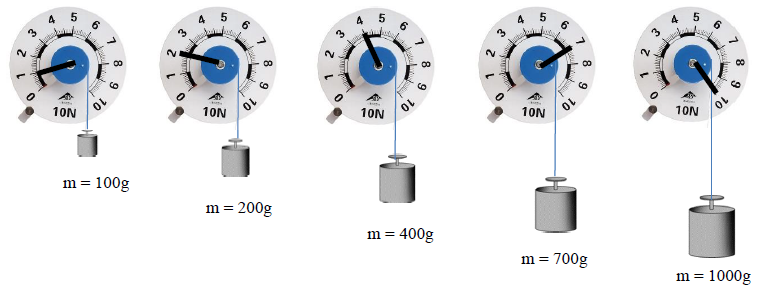
1) Compléter le tableau de mesures suivants :
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Masse }m\text{ (en }g)&0&100&200&400&700&1000\\\hline\text{Poids }P\text{ (en }N)&&&&&&\\\hline\end{array}$$
2) Sur le papier millimétré, construire la courbe donnant le poids $P$ en fonction de la masse $m.$
3) Quelle est l'allure de la courbe obtenue ?
4) Que peut-on en déduire pour le poids et la masse ?
Exercice 6 : Réalisation d'un dynamomètre
Donnée : on prendra $g=10\;N.kg^{-1}$
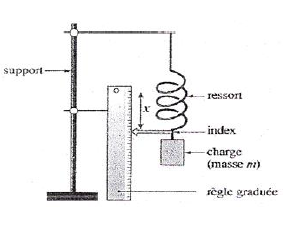
Pour réaliser un dynamomètre à l'aide d'un ressort, on effectue un étalonnage.
Pour cela, le ressort est suspendu à un point fixe par une de ses extrémités.
L'autre extrémité porte un index et se déplace devant une règle maintenue verticalement par un support fixe.
On accroche à l'extrémité libre différente masses marquées et on lit, à l'équilibre, les indications correspondantes de l'index sur la règle graduée.
On obtient :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline m\;(kg)&0&0.20&0.40&0.60&0.80&1&1.20&1.40&1.60&1.80&2\\ \hline x\;(cm)&0&2.6&5.2&8&10.7&13.3&16&18.6&21.5&24&26.5\\ \hline\end{array}$$
1) On considère le système "masse marquée" dans le référentiel terrestre.
a) Quelles sont les forces qui agissent sur le système à l'équilibre ?
(Donner toutes les caractéristiques sans calculer aucune norme).
b) Que peut-on dire de la somme de ces forces et pourquoi ?
c) En déduire une relation entre $m$ (valeur de la masse suspendue) et $T$ (norme de la force exercée par le ressort sur la masse).
2) Construire le graphique donnant $T$ en fonction de $x.$ Que représente cette longueur ?
3) En déduire, en justifiant, la valeur de la raideur du ressort et son unité.
Applications :
4.a) On souhaite se servir du dispositif réalisé pour déterminer le volume d'une boite.
On suspend la boite à l'extrémité libre du ressort : l'index indique alors: $x_{1}=16\;cm.$
En déduire sa masse en utilisant le graphique.
b) On immerge maintenant complètement la boite dans une bassine remplie d'eau de façon à ce que la boite ne touche aucune paroi.
L'index indique alors $x_{2}=10\;cm$
$-\ $ Pourquoi la valeur indiquée par l'index a-t-elle diminuée ?
$-\ $ Faire un schéma des forces appliquées sur le système.
$-\ $ En déduire l'expression littérale du volume de la boite. Calculer sa valeur.
5) On utilise maintenant le ressort pour tester la résistance d'une colle.
Pour cela, on colle un petit disque en plastique sur un support et on laisse bien sécher.
On fixe ensuite une extrémité du ressort au centre du disque. On tend lentement le ressort, perpendiculairement au disque, jusqu'à l'arrachement
Juste avant que le disque ne se décolle, le ressort était étiré de $20\;cm.$
Déterminer graphiquement la valeur de la force nécessaire pour produire l'arrachement
Exercice 7
Pour déterminer la densité du fer, on réalise les deux expériences suivantes :
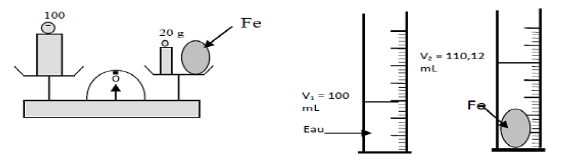
1) Déterminer la masse $m$ du fer.
2) Déterminer le volume $V$ du fer
3) En déduire la masse volumique $\rho_{Fer}$ du fer dans SI.
4) Calculer la densité $d$ du fer. Sachant que $\rho_{eau}=1\;g.cm^{-3}$
5) Expliquer Pourquoi si on lance un clou de fer dans l'eau il tombe au fond
Exercice 8
Un solide plein en fer de forme cubique et d'arête $a=2\;cm$ a une masse $m_{fer}=63.2\;g$
1) Déterminer, en $cm^{3}$, le volume $V$ du solide.
2) Proposer une autre méthode permettant de déterminer ce volume. Faire un schéma.
3) a) Rappeler l'expression de la masse volumique en précisant la signification de chaque terme.
b) Montrer que la masse volumique du fer est $\rho_{fer}=7,9 g.cm^{-3}$.
4) On réalise les équilibres suivants :
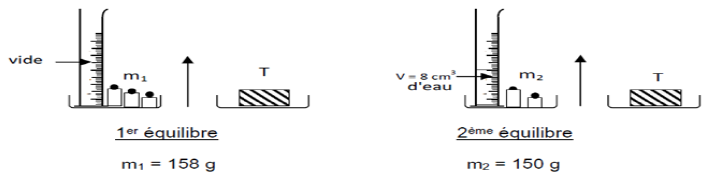
4) a) Déterminer, en $g$, la masse $m$ eau du volume $V=8\;cm^{3}$ d'eau.
4) b) Exprimer la densité d du fer par rapport à l'eau en fonction de $m_{fer}$ et $m_{eau}.$
4) c) Calculer $d.$
4) d) Le fer flotte-t-il sur l'eau ? Justifier la réponse.
Exercice 9
Un cylindre plein en plomb à une hauteur de $10\;cm$ et de rayon de $2\;cm$
La pesée de ce cylindre est représentée par la figure

On donne : $m=1,5\;kg\;,\ m_{1}=80\;g$ ; la masse volumique de l'eau $\rho_{e}=1000\;kg.m^{-3}$
1.a) Calculer le volume de cylindre
b) Déterminer sa masse
2.a) Déduire la masse volumique du plomb en $g.cm^{-3}$ puis en $kg.m^{-3}$
b) Déterminer la densité du plomb par rapport à l'eau
c) Si on introduit ce cylindre dans une éprouvette non graduée contient de l'eau quelle sera alors la hauteur de l'eau dans l'éprouvette ?
3) Un morceau de fer de forme sphérique de masse $m=7.9\;g$ déterminer le volume de ce sphère sachant que la densité du fer $d_{fer}=7900.$
Exercice 10
On réalise les équilibres suivants en utilisant la même tare, le liquide utiliser et l'huile
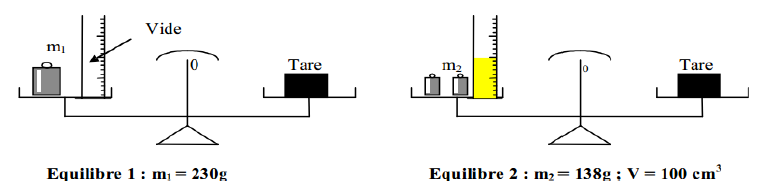
1) Écrire les égalités correspondantes pour chaque équilibre
2) Déduire la masse de l'huile
3) Déterminer la masse volumique de l'huile en $g.cm^{-3}\ $ et $\ kg.m^{-3}$
4) Déterminer la densité de l'huile par rapport à l'eau. Conclure
On donne $\rho_{e}=1\;g.cm^{-3}$
5) Si on refait les mêmes expériences on remplace l'huile par $10\;cm^{3}$ de mercure on trouve $m_{1}=230\;g\ $ et $\ m_{2}=94\;g$
a) Déterminer la masse de mercure
b) Déterminer la masse volumique du mercure en $g.cm^{-3}\ $ et $\ kg.m^{-3}$
c) Déterminer la densité du mercure par rapport à l'eau. Conclure
6) On mélange dans un récipient de l'eau, de l'huile et du mercure représenter sur un schéma le mélange hétérogène obtenu expliquer
Exercice 11
Un pavé flotte à la surface de l'eau. Ses dimensions sont : hauteur : $20\;cm$ ; longueur : $60\;cm$ ; largeur : $20\;cm$
1) Le pavé émerge sur une hauteur de $3\;cm.$ Calculer le volume de la partie immergée.
2) Calculer la masse d'eau déplacée. $\rho_{eau}=1000\;kg.m^{-3}$
3) Calculer le poids d'eau déplacé et en déduire la valeur du poids du pavé. $g=10\;N.kg^{-1}$
4) Calculer la masse du pavé.
5) a) Calculer le volume du pavé.
b) Préciser le matériau constituant ce pavé :
$$\begin{array}{|l|c|c|c|c|c|}\hline\text{Matériau}&\text{Polystyrène}&\text{Bois}&\text{Glace}&\text{Aluminium}&\text{Fer}\\\hline\text{Masse volumique }kg.m^{-3}&11&850&920&2700&8000\\\hline\end{array}$$
Exercice 12
Un iceberg a un volume total $V_{T}= 600\;m^{3}$
Sa masse volumique (glace) est $\rho_{1}=910\;kg.m^{-3}$, celle de l'eau de mer est $\rho_{2}=1024\;kg.m^{-3}$
1) Schématiser l'iceberg flottant et préciser les forces auxquelles il est soumis lorsqu'il est à l'équilibre.
2) Calculer la masse totale de l'iceberg.
3) Calculer le volume immergé (sous l'eau) $V_{i}$ de l'iceberg
4) Trouver une relation entre le Volume immergé $V_{i}$ , le volume total $V_{T}$ et les masses volumiques.
5) En déduire la proportion (pourcentage) de glace immergée dans cet iceberg.
Exercice 13 : Sur la Lune
Lors d'une mission lunaire, un astronaute a mesuré les poids $P$ de différents objets de masses $m$ connues.
Il obtient les résultats suivants :
$$\begin{array}{|c|c|c|c|c|c|}\hline m\;(kg)&0.30&0.50&0.80&1.10&1.50\\ \hline P\;(N)&0.49&0.82&1.30&1.79&2.45\\ \hline\end{array}$$
1) Tracer la courbe traduisant la variation de P en fonction de $m.$ Tu prendras :
$-\ $ en abscisse, $0.5\;cm$ pour $0.10\;kg$
$-\ $ en ordonnées, $0.5\;cm$ pour $0.20\;N$
2) En Déduire la valeur de l'intensité de la pesanteur lunaire $g$ (On expliquera la démarche)
3) L'expression de l'intensité de la pesanteur à la surface de la Lune est donnée, en première approximation, par la relation :
$g=6.67.10^{-11}\dfrac{M}{R^{2}}$ où $M\ $ et $\ R$ sont respectivement la masse en kilogramme de la Lune et son rayon en mètre.
$R=1738000\;m$
En déduire la masse de la Lune
Exercice 14
François soupçonne que les petits soldats avec lesquels il joue ne sont pas en plomb.
Il dispose d'échantillons de plusieurs métaux gris (argent, zinc, fer et plomb), d'une éprouvette graduée et d'une balance électronique.
François fait ses mesures et remplit le tableau suivant. N'ayant pas vidé son éprouvette il la renverse sur sa feuille de résultats et se retrouve avec une feuille à trous
$$\begin{array}{|l|c|c|c|c|c|}\hline\text{Métal}&\text{Fer}&\text{Plomb}&\text{Zinc}&\text{Argent}&\text{Soldat}\\ \hline\text{Masse de l'échantillon }(g)&45&&29.7&76.9&81.4\\ \hline\text{volume de l'échantillon }(ml)&&6.5&11&&7.2\\ \hline\text{Masse volumique }(g.ml^{-1})&7.8&11.3& &10.5& \\ \hline\end{array}$$
1) Expliquer en quelques phrases comment il doit s'y prendre pour vérifier la composition de ses soldats.
2) A quoi va servir l'éprouvette graduée ? Comment va-t-il s'en servir ?
3) Recopier et compléter le tableau en faisant apparaître tous les calculs.
4) Conclure quant au soupçon de François. Justifier
Exercice 15 : Équilibre d'un iceberg
Rappel : Théorème d'Archimède : "tout corps immergé dans un fluide subit de la part de celui-ci, une poussée verticale, de bas vers le haut, égale au poids du fluide déplacé"
On considère un iceberg de volume total $V$ et de volume émergé $V'.$
1) Schématiser l'iceberg dans son état d'équilibre (les 3/4 de sa hauteur sont immergés).
2) Faire le bilan des forces appliquées à l'iceberg. Représenter ces forces sans considération d'échelle.
3) Énoncer la condition d'équilibre de l'iceberg. En déduire l'expression de $V$ en fonction de $\rho_{e}$ (masse volumique de l'eau), $\rho_{i}$ (masse volumique de l'iceberg) et $V’.$
4) Calculer alors dans l'ordre $V$ et la masse $M$ de l'iceberg.
Données : $\rho_{i}=910\;kg.m^{-3}\;;\ \rho_{e}=1024\;kg.m^{-3}\;;\ V'=600\;m^{3}$
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Commentaires
Anonyme (non vérifié)
sam, 12/12/2020 - 23:32
Permalien
Hhh
Anonyme (non vérifié)
jeu, 02/11/2021 - 23:39
Permalien
Correction
Sall (non vérifié)
dim, 03/14/2021 - 15:11
Permalien
Solution
Anonyme (non vérifié)
dim, 02/28/2021 - 16:30
Permalien
Pourquoi cette exercice n'a
Anonyme (non vérifié)
sam, 03/13/2021 - 18:38
Permalien
pourqoui cet exercice n'a pas
Paco Diaz (non vérifié)
sam, 03/13/2021 - 18:41
Permalien
Intéressant mais c'est la
Paco Diaz (non vérifié)
sam, 03/13/2021 - 18:41
Permalien
Intéressant mais c'est la
mouna (non vérifié)
sam, 03/20/2021 - 01:33
Permalien
les solutions
Serigne Ndiaye (non vérifié)
lun, 06/07/2021 - 02:34
Permalien
Pour être excellent
Adama Touré (non vérifié)
mar, 06/14/2022 - 01:27
Permalien
Élèves
Sissoko (non vérifié)
dim, 03/05/2023 - 13:00
Permalien
Être scientifique
J B N (non vérifié)
sam, 04/01/2023 - 23:14
Permalien
correction
Lalatre (non vérifié)
mer, 02/05/2025 - 06:14
Permalien
Remerciements
Ajouter un commentaire