Vous êtes ici

Série d'exercices : Propagation rectiligne de la lumière - 2nd S

Classe:

Seconde

Exercice 1

Dans les exemples proposés, choisir quels sont les objets lumineux qui sont des sources primaires, et ceux qui sont des sources secondaires.

Donner les résultats sous forme d'un tableau.

Flamme de bougie, mur blanc, lune, soleil, vénus, étoile polaire, satellite Spot, atmosphère (le ciel), écran de télévision, écran de projection

Exercice 2

Compléter :

Les$\ldots\ldots$produisent la lumière qu'elles émettent.

Les sources secondaires sont des objets lumineux$\ldots\ldots$par des sources primaires.

La lumière émise par les sources se propage$\ldots\ldots$, dans un milieu$\ldots\ldots$et homogène.

On traduit ce type de propagation la construction de droites orientées appelées$\ldots\ldots$

Vocabulaire qui peut être employé

Rayon, transparent, source, éclairé, primaire, isotrope, rectiligne ment, inférieure, supérieure.

Exercice 3

a) La distance de la terre au soleil est environ de $150000000\;km.$ Combien de temps met la lumière à nous parvenir ?

b) Pour mesurer la distance de la terre à la lune, les astronomes émettent un faisceau laser vers un réflecteur que les astronautes ont placé sur la lune.

Le temps mis par la lumière pour revenir à l'observatoire est à un moment de l'année de $2.6\;s$

Quelle est la distance de la terre à la lune ?

Exercice 4

1) Qu'est-ce qu'un milieu transparent ?

2) Qu'est-ce qu'un milieu homogène ?

3) Donner des exemples de milieux transparents et homogènes.

4) Comment la lumière se propage-t-elle dans un tel milieu ?

Exercice 5

Le personnage voit une fleur dans le jardin

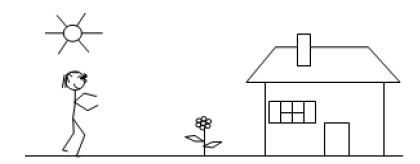
Dessiner et orienter le parcours de la lumière afin de décrire au mieux ce phénomène

Exercice 6

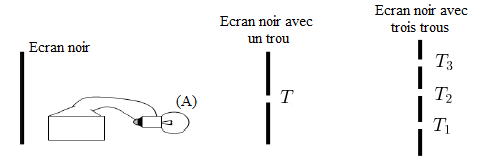
L'ampoule $(A)$ est branchée, prévoir par quel trou, $T_{1}\;,\ T_{2}\;,\ T_{3}$ un observateur peut voir de la lumière.

Utiliser le modèle de l'optique élémentaire pour réaliser vos prévisions

Exercice 7

Parmi les hypothèses suivantes, choisir celle(s) qui est (sont) possible(s).

1) la vue arrive aux objets si la lumière les éclaire.

2) la lumière éclaire l'œil, rebondit vers les objets et retourne à l'œil.

3) si vous voyez vos pieds c'est qu'ils émettent de la lumière.

4) la lumière éclaire les objets et elle est renvoyée vers l'œil.

5) l'œil voit les objets quand la vue est suffisamment forte pour y arriver : la vue est d'autant plus forte que la lumière ambiante est importante

Exercice 8

On considère une source ponctuelle S , une petite sphère de rayon $r=2\;cm$ et un écran placé à la distance $D=2.0\;m$ de la source $S.$

La sphère est placée à la distance $d=0.5\;m$ de la source ponctuelle de telle façon que l'on puisse voir son ombre portée sur l'écran. La source $S$ et les centres de l'écran et de la sphère sont alignés.

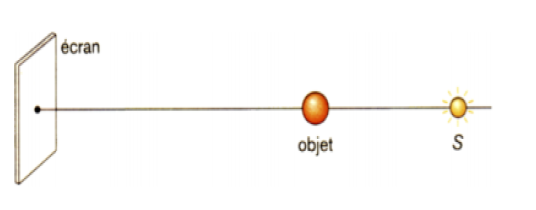
1) Quelle est la nature géométrique de l'ombre portée sur l'écran ?

2) Évaluer les dimensions de cette ombre portée, ainsi que sa surface.

3) On remplace la sphère par un disque de même rayon, à quelles conditions peut-on obtenir sur l'écran la même ombre portée qu'avec la sphère ?

Exercice 9

Des réflecteurs ont été déposés à la surface de la Lune lors des différentes missions lunaires Apollo.

Depuis la Terre, on vise un réflecteur à l'aide d'un faisceau laser et on mesure la durée $t$ séparant l'émission de la réception.

Lors d'une expérience, on a trouvé : $t=2.51\;s$

1) Déterminer la distance entre les surfaces des deux astres.

2) En déduire la distance entre leurs centres.

Données : rayon de la Terre $R_{T}=6.40\;10^{3}\;km$, rayon de la Lune $R_{L}=1.74\;10^{3}\;km$

Exercice 10

À partir d'une boîte parallélépipédique, Julien construit une chambre noire.

Puis il place face au trou (noté $O$) de diamètre $d=1\;mm$ un filament lumineux rectiligne $AB$ de hauteur $10\;cm$ ($O'$ milieu de $AB$) et d'épaisseur négligeable.

Le filament est disposé parallèlement à la face translucide, sa distance au trou $O$ est $D=60\;cm.$

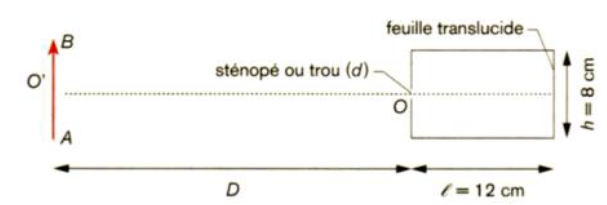
1) En considérant le trou $O$ ponctuel et en utilisant des rayons lumineux issus de $A\ $ et $\ B.$

Montrer que l'œil de Julien placé derrière la feuille translucide voit une reproduction du filament renversée sur la feuille (on parlera d'image $A’B’)$, puis déterminer la taille de l'image $A’B’$

2) Montrer sur un schéma en vue du dessus avec deux rayons issus de $O’$ que le diamètre du trou influe sur la netteté de l'image.

Établir la relation qui lie la largeur $e$ de l'image à la distance $D$ et aux caractéristiques de la chambre noire $(l\ $ et $\ d)$ puis calculer $e$