Série d'exercices sur Acide fort - base forte Réaction acide fort - base forte - Ts
Classe:
Terminale
Exercice 1
La combustion complète d'un échantillon d'acide butyrique (A) de masse m=1.35g fournit 2.7g de dioxyde de carbone CO2 et 1.1g d'eau.
1) Calculer la masse de carbone d'hydrogène et d'oxygène contenue dans cette échantillon.
2) a) En déduire la composition massique centésimale (pourcentage de carbone, d'hydrogène et d'oxygène)
b) Montrer que la formule brute de (A) est C4H8O2, sachant que sa masse molaire est M=88g⋅mol−1
3) Une solution aqueuse (s) obtenue en faisant dissoudre 0.1mol d'acide butyrique (acide faible) dans 500mL d'eau.
a) Rappeler la définition d'un acide de Bronsted
b) Écrire l'équation chimique de la réaction de cet acide dans l'eau
c) Quels sont les comptes acide base mis en jeu ?
d) Calculer la concentration molaire C de la solution obtenue.
On donne :
MH=1g⋅mol−1 ; Mc=12g⋅mol−1 ; MO=16g⋅mol−1.
Exercice 2
on souhaite préparer 100mL d'une solution S0 d'acide benzoique C6H5COOH de concentration molaire volumique C0=0.1mol⋅L−1
1) Déterminer la masse de cristaux à peser pour préparer S0.
2) La solution S0 a un pH=2.6
a) Écrire l'équation bilan de la réaction de l'acide benzoique avec l'eau.
Monter que cet acide n'est pas un acide fort.
b) Déterminer le coefficient de dissociation α0=[C6H5COO−]C0 de l'acide dans S0.
3) On réalise une solution S1 par dilution au 1/10 de la solution S0.
S1 a un pH=3.1.
En déduire le coefficient α1 de l'acide dans la solution S1 et conclure.
Exercice 3
Les mesures sont effectuées à 25∘C.
Couples acide/base :
acide benzoique/ion benzoate : pKa=4.2
couples de l'eau : H2O/HO− : pKa=14
Étude du couple acide benzoique/ion benzoate : C6H5COOH/C6H5COO−.
1) On mesure le pH d'une solution S1 d'acide benzoique de concentration c1=1.0⋅10−2mol⋅L−1.
Le pH−mètre indique 3.1.
a) Pourquoi cette mesure permet-elle d'affirmer que l'acide benzoique est un acide faible dans l'eau ?
Justifier.
b) Écrire l'équation-bilan de la réaction de l'acide benzoique avec l'eau.
Donner l'expression de la constante d'acidité du couple considéré.
2) On mesure ensuite le pH d'une solution S2 de benzoate de sodium de concentration c2=1.0⋅10−2mol⋅L−1.
On trouve pH=8.1.
Le benzoate de sodium (C6H5COONa) est un corps pur ionique dont les ions se dispersent totalement en solution.
a) Pourquoi la mesure du pH réalisée permet-elle d'affirmer que l'ion benzoate est une base faible dans l'eau ?
Justifier.
b) Écrire l'équation-bilan de la réaction de l'ion benzoate avec l'eau.
Exprimer la constante de cette réaction et calculer sa valeur.
3) On ajoute à la solution S1 quelques gouttes d'une solution de soude.
Le pH prend alors la valeur 5.2.
a) Indiquer, sans calcul, en utilisant une échelle de pH, quelle est l'espèce du couple qui prédomine dans la solution obtenue.
b) Noter, sur une échelle des pKa, les différents couples acide/base qui interviennent dans la solution S1 et dans la solution de soude.
c) Écrire l'équation- bilan de la réaction acide/base qui se produit lors du mélange de la solution S1 et de la solution de soude.
− Calculer la constante de cette réaction.
− En déduire si la réaction peut être considérée ou non comme totale.
4) On réalise une solution S en mélangeant 20cm3 de solution S1 et 20cm3 de solution S2.
A partir de la réaction se produisent lors du mélange, déduire, sans calcul, que la concentration de l'acide benzoique, dans la solution S, est égale à celle de sa base conjuguée.
En déduire la valeur du pH de la solution S.
Exercice 4
On donne M(C)=12g⋅mol−1, M(H)=1g⋅mol−1 et M(O)=16g⋅mol−1.
Un acide carboxylique (A) à chaine linéaire, de masse molaire M=88g⋅mol−1.
1) a) Donner la formule brute d'un acide carboxylique et montrer que sa masse molaire s'écrit sous la forme M=14n+32 avec n est le nombre de carbone contenu dans sa formule.
b) Déterminer la formule semi- développée et le nom de chaque isomère acide de (A).
2) L'isomère à chaine ramifié de (A) est obtenu par une réaction chimique à partir d'un alcool (B).
a) Donner le nom de la réaction.
b) Écrire l'équation chimique de cette réaction.
c) Donner le nom de l'ester formé.
4) On dissout une masse m d'acide (A) dans de l'eau distillée afin de préparer 100mL de solution de concentration molaire C=0.01mol⋅L−1.
En mesurant le pH de cette solution, on trouve qu'il est égal à 3.9.
Calculer la masse m.
b) Calculer la concentration en ions H3O+.
L'acide (A) est-il faible ou fort ?
On rappelle que [H3O+]=10−pH
c) Écrire l'équation de dissolution de l'acide (A) dans l'eau.
Exercice 5
On dispose du matériel et des produits suivants :
− Pipettes de 5mL, 10mL et 2mL
− Fioles jaugées de 500mL, 250mL et 100mL
− Une solution de méthylamine de concentration C1.
− Une solution de base B de concentration C2.
− Eau distillée - des flacons
Deux flacons A et B contenant l'un une solution S1 de méthylamine et l'autre une solution S2 de base B.
La mesure de pH de la solution S1 donne pH1=11.85 et celui de S2 est pH2=12.
Afin de connaitre la force de chaque base, on effectue un prélèvement de chaque flacon que l'on soumet à une dilution au dixième.
La mesure des pH donne pH1=11.35 et celui de pH2=11.
1) a) Montrer, en le justifiant que le méthylamine est une base faible alors que B est une base forte.
b) Calculer C2.
c) Déduire la démarche expérimentale à suivre, en précisant le matériel choisit pour effectuer la dilution au dixième.
2) Établir que le pH de la solution S1 vérifie la relation suivante pH=12(pKa+pKe+logC).
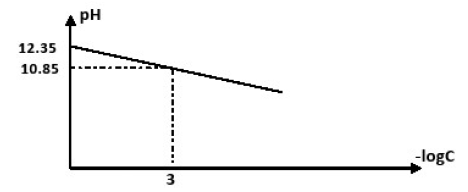
3) A l'aide d'un protocole expérimentale, on mesure le pH d'une solution aqueuse de méthylamine pour différentes valeurs de sa concentration C.
Les résultats des mesures permettent de tracer la courbe pH=f(−logC).
Déduire de cette courbe la valeur de pKa du couple CH3NH+3/CH3NH2 ainsi que la concentration C de la solution S.
Exercice 6
On considère quatre solutions acides, de même concentration C=10−2mol/L.
Les pH de ces solutions, mesurés à 25∘C sont indiqués dans le tableau suivant :
Solution d'acideA1HA2HA3HA4HpH3.425.62.9
1) a) Qu'appelle-t-on acide fort ?
Qu'appelle-t-on acide faible ?
b) En utilisant le tableau ci-dessus, préciser le(s) acide(s) faible(s) et le(s) acide(s) fort(s).
2) a) Pour chaque acide faible, calculer le coefficient de dissociation de l'acide dans l'eau.
Classer ces acides, selon leur force.
b) Écrire une relation entre la constante d'acidité Ka du couple AH/A− et le coefficient de dissociation de l'acide dans l'eau.
c) Calculer la constante d'acidité Ka de chaque acide faible.
Classer respectivement ces acides selon leur Ka respectives.
3) on dilue 10 fois la solutions n∘1 le PH alors égale à 3.9.
Quelle est la nouvelle valeur du coefficient de dissociation de l'acide A1H
Comparer au coefficient de dissociation de l'acide A1H/A−1.
Exercice 7
On prépare un volume V1=200mL d'une solution aqueuse S d'hypo chlorate de sodium ClONa de concentration C0=10−1mol⋅L−1, en dissolvant une masse m de ce sel dans l'eau.
Le pH de la solution obtenue est pH0=9.75.
1) Déterminer la masse m.
(MCl=35.5 ; MO=16 et MNa=23 en g⋅mol−1).
Écrire l'équation de la réaction qui accompagne la dissolution.
4) Donner l'expression de Kb en fonction de Ke, pH0 et C0 puis calculer sa valeur.
5) On prélève un volume v0=10mL et on ajoute un volume V d'eau.
Soit C la concentration de la nouvelle solution.
a) Donner une relation entre C, C0, V0 et V.
b) Montrer que pH=pH0−12log(1+VV0).
c) Calculer le pH de la solution pour V=90mL et en déduire les concentrations de ClO− et HClO.
Exercice 8
Après plusieurs heures de pédalage sous la pluie, le groupe décide de s'arrêter déjeuner dans une auberge.
1. Il y a sur la table une bouteille d'eau et un soda.
Le pH de l'eau minérale indiqué sur l'étiquette est 6.3.
1.1 Montrer que la concentration en ion oxonium [H3O+] de cette eau minérale est voisine de 5.0⋅10−7mol⋅L−1.
1.2 Calculer la quantité de matière d'ion oxonium n(H3O+) contenue dans cette bouteille de volume V=1.5L.
2. Sur l'étiquette du soda on peut lire, entre autre : conservateur : benzoate de sodium.
L'ion benzoate C6H5−COO− est une base, il fait partie du couple "acide benzoique/ion benzoate" dont le pKa est 4.2.
2.1 Donner la définition d'une base selon Bronsted.
2.2 Écrire la réaction susceptible de se produire entre l'ion benzoate et l'eau.
Nommer les produits obtenus.
2.3 Donner l'expression littérale de la constante d'acidité du couple acide benzoique/ion benzoate.
2.4 Le pKa de ce couple est 4.2.
Représenter sur un axe gradué en pH, le diagramme de prédominance de l'acide benzoique et de l'ion benzoate.
2.5 Le pH de l'estomac est égal à 2.
En s'aidant du diagramme précédent, dire ce qu'il advient de l'ion benzoate lorsque Rémi a avalé la boisson.
Reste-t-il sous forme d'ion benzoate ou se transforme-t-il en acide benzoique ?
Justifier.
Le repas étant très copieux, le restaurateur propose à Rémi une boisson facilitant la digestion en oubliant de lui dire qu'elle contient de l'alcool.
Rémi accepte...
Exercice 9
Toutes les solutions sont prises à 25∘C, température à laquelle le produit ionique de l'eau pure est Ke=10−14.
En dissolvant chacune des trois bases B1, B2 et B3 dans de l'eau pure, on prépare respectivement trois solutions aqueuses basiques (S1), (S2) et (S3) de concentrations initiales identiques C1=C2=C3.
On oublie de coller une étiquette portant le nom de la solution sur chaque flacon.
Seule l'une des bases correspond à une base forte (l'hydroxyde de sodium NaOH).
Chacune des deux autres étant une base faible.
Pour identifier chaque solution, on mesure son pH et on porte les résultats dans le tableau suivant :
(S1)(S2)(S3)pH11.11310.6
1) a) Classer les bases B1, B2 et B3 par ordre de force croissance ; justifier le choix adopté.
b) En déduire celle des trois bases qui correspond à NaOH ; déterminer la valeur de la concentration de sa solution.
2) a) Exprimer le pKa d'une solution de base faible B en fonction de son pH, de sa concentration initiale c et du pKe.
B est l'une des deux bases faibles utilisées dans l'expression décrite ci-dessus.
On supposera que, suite à la dissolution, la concentration de la base restante est pratiquement égale à c.
b) Calculer le pKa de chacune des deux bases faibles.
c) Identifier chacune des deux bases faibles en utilisant la liste des valeurs de pKa de quelques bases consignées dans le tableau suivant :
AziridineMorphineAmmoniacEphedrineEthylaminepKa8.018.219.2599610.7
Exercice 10
A. Pour déboucher les canalisations, on utilise des produits domestiques qui sont des solutions concentrées d'hydroxyde de sodium (ou soude).
Sur l'étiquette de l'un de ces produits, on lit
− densité : d=l.2 (soit une masse volumique p=l.2g⋅cm–3,
− contient 20% en masse de soude.
1. Montrer que la concentration molaire C de la solution commerciale est voisine de 6mol⋅L–1
2. Quel volume de solution commerciale faut-il prélever pour obtenir 1L de solution diluée de concentration C1=3×10–2mol⋅L−1 ?
3. Quel volume de solution commerciale faut-il prélever pour obtenir 1L de solution diluée de concentration C1=3×10–2mol⋅L−1 ?
B. Les solutions de soude sont des solutions de base forte.
1.1 Rappeler la définition d'une base forte.
1.2 Calculer le pH de la solution diluée.
Pour vérifier sa concentration, on dose 5mL de la solution diluée par une solution d'acide chlorhydrique de concentration Ca=10–2mol⋅L–1.
2.1 Écrire l'équation-bilan de la réaction.
2.2 Pour obtenir l'équivalence, on doit verser 15mL de la solution d'acide chlorhydrique.
Calculer la concentration de la solution diluée.
Retrouve-t-on la valeur souhaitée ?
Masses atomiques (molaires) :
Oxygène : 16g⋅mol–1 ;
Hydrogène : 1g⋅mol–1 ;
Sodium : 23g⋅mol–1
Exercice 11
N.B :
Toutes les solutions sont considérées à 25∘C où [H3O+][OH−]=10−14
1. Qu'appelle-t-on base forte ?
2. On prépare une solution d'hydroxyde de sodium NaOH (base forte) en faisant dissoudre une masse m de NaOH dans l'eau pure de façon à obtenir 2L de solution S.
2.1 Écrire l'équation de la dissolution du solide dans l'eau.
2.2 Quelles sont les entités chimiques présentes dans la solution ?
2.3 Comment peut-on mettre en évidence expérimentalement le caractère basique de la solution.
2.4 A l'aide d'un pH−mètre on mesure le pH de la solution, on trouve pH=11
Calculer la concentration molaire de toutes les entités chimiques présentes en solution.
2.5 Quelle est la concentration molaire C de la solution.
Calculer alors m.
On donne : MNa=23g⋅mol−1 ;
MO=16g⋅mol−1 ;
MH=1g⋅mol−1
3. A partir de la solution précédente, on veut obtenir un litre d'une solution S′ d'hydroxyde de sodium de pH=10 et de concentration C′.
3.1 Calculer la concentration molaire C′ de la solution S′.
3.2 Indiquer d'une façon précise comment doit-on opérer pour préparer la solution S′
Exercice 12
On dispose d'une solution d'acide sulfurique S0 de concentration molaire C0=2mol⋅L−1
A partir de la solution S0, on veut préparer une solution S1 de concentration C1=0.2mol⋅L−1 et volume V1
Sur la paillasse, on dispose du matériel suivant : deux pipettes jaugées (avec des propipettes) de 10mL et 20mL ; deux béchers de 150mL et 200mL ; une pissette de 300mL ; une fiole jaugée de 200mL ; une burette de 50mL et tous les autres produits nécessaires
1. Calculer le volume V0 de la solution S0 à prélever pour un volume V1=200mL de la solution de S1
2. Décrire brièvement le mode opératoire de cette opération
3. On veut vérifier la concentration des ions hydroniums dans cette par dosage à l'aide d'une solution d'hydroxyde de sodium S2 de concentration C2=0.2mol⋅L−1
Pour cela, on prélève 10mL de la solution S1
3.1 Faire le schéma simplifié du dispositif de dosage expérimental utilisé pour ce dosage
3.2 On introduit quelques gouttes de phénolphtaléine dans l'échantillon de S1 prélevé
3.2.1 Quelle est la couleur de la solution ?
3.2.2 Comment repère-t-on l'équivalence au cours du dosage ?
3.2.3 La zone de virage d'un indicateur coloré est située entre pH=3.2 et pH=4.4
Cet indicateur peut-il être utilisé dans ce dosage ?
Justifier
3.3 On obtient l'équivalence lorsqu'on a versé 20mL de solution S2
3.3.1 Quelle est la concentration molaire des ions hydroniums ?
3.3.2 Ce résultat était-il prévisible ?
Justifier la réponse
Exercice 13
Mélange de solution d'acide chlorhydrique et de potasse
On dispose au laboratoire des solutions suivantes :
Solution A : solution aqueuse d'acide chlorhydrique de concentration molaire Ca
Solution B : solution aqueuse d'hydroxyde de potassium de concentration molaire Cb
Un volume VA de la solution A est obtenu en mettant en solution un volume V′A de chlorure d'hydrogène gazeux.
Le volume molaire gazeux est noté Vm dans les conditions de l'expérience
Le volume VB de solution B est obtenu en mettant en solution une masse mB d'hydroxyde de potassium
Données :
VA=100L ;
V′A=100L ;
mB=11.2g ;
VB=10L ;
Vm=25L/mol
Masse atomique (g/mol)
K=39 ;
O=16 ;
H=1.
Produit ionique de l'eau Ke=1014 à 25∘C
1. Exprimer littéralement puis calculer CA
2. Exprimer littéralement puis calculer CB
3. On mélange le tiers de VA au quart de VB
− Écrire les équations de mise en solution aqueuse du solide et du gaz, solutés des solutions ; l'équation bilan de la réaction se produisant dans le mélange
− Définir l'équivalence acido-basique.
Le mélange est-il à l'équivalence ?
Justifier.
− Ce mélange à 25∘C est-il acide ou basique ?
Justifier
Mélangeons cette fois un volume V1 de la solution A et un volume V2 de la solution B tels que :
V2=xV1 et que le pH du mélange soit 12 à 25∘C.
4. Mélangeons cette fois un volume V1 de la solution A et un volume V2 de la solution B tels que V2=xV1 et que le pH du mélange soit 12 à 25°C.
− Calculer x
− Dans le cas de cette dernière préparation quel est le plus grand volume de mélange possible ?
Exercice 14
On mélange un volume VA d'une solution d'acide chlorhydrique (H3O++Cl−) de concentration molaire CA ayant un pHA avec un volume VB d'une solution d'hydroxyde de sodium (Na++OH−) de concentration molaire CB ayant un pHB.
a) Réaliser le bilan de matière des ions hydronium et hydroxyde.
b) Calculer leur concentration molaire dans la solution après la réaction de neutralisation.
c) En déduire le pH de la solution obtenue.
Montrer que celui-ci est :
− pH=7, dans le cas d'une réaction totale et stœchiométrique.
− pH=−log(CAVA−CBVBVA+VB), dans le cas d'un excès de la solution acide.
− pH=14+log(CBVB−CAVAVB+VA), dans le cas d'un excès de la solution basique.
d) Calculer la concentration molaire des ions sodium et des ions chlorure qui sont restés dans la solution dans les trois cas
1) VA=200mL, pHA=2.0
et VB=200mL, pHB=12.0.
2) VA=800mL, pHA=2.0
et VB=500mL, pHB=12.0.
3) VA=300mL, pHA=2.0
et VB=200mL, pHB=12.3.
Exercice 15
On dispose de deux solutions aqueuses de concentration molaire C dans des récipients sur les quels manquent des étiquettes : C=1.10−3mol⋅L−1.
On dispose également d'étiquettes sur lesquelles sont inscrites les indications suivantes :
H3O+ ; Cl−) et Na+ ; OH.
a) Calculer les pH théoriques d'une solution d'acide chlorhydrique et d'une solution d'hydroxyde de sodium de même concentration C.
On désire retrouver par des mesures de pH à quel flacon correspond chaque étiquette.
On obtient les mesures suivantes :
Flaconn∘1n∘2pH mesuré2.9011.2
b) Indiquer, pour chaque flacon, l'étiquette qui lui correspond
Exercice 16
On verse dans va=200cm3 d'acide chlorhydrique une solution de soude (cb=0.5mol/L).
On mesure le pH en fonction du volume vb de soude versé
V(cm3)01.02.02.53.04.04.54.95.05.15.56.06.010.012.01.92.02.12.22.32.62.93.65.110.311.011.311.611.811.9
1. Tracer la courbe pH=f(vb) : 1cm pour 1 unité pH et 2cm pour 1cm3
2. Déterminer le point d'équivalence par la méthode des tangentes.
Quel est le pH à l'équivalence ?
3. En déduire la concentration cade la solution d'acide.
4. Calculer les diverses concentrations pour vb=3cm3
Commentaires
Procore (non vérifié)
mar, 07/14/2020 - 23:31
Permalien
Recherche du Bac
1 (non vérifié)
sam, 11/12/2022 - 14:45
Permalien
7
Anonyme (non vérifié)
sam, 11/12/2022 - 14:46
Permalien
Comment traiter les exercices
Memel (non vérifié)
jeu, 03/02/2023 - 07:34
Permalien
Élève
Ajouter un commentaire