Solution des exercices : acide - base - Ts

 

1) Masse de carbone, d'hydrogène et d'oxygène contenue dans l'échantillon.

 

$\begin{array}{lcl} \dfrac{m_{C}}{M_{C}}&=&\dfrac{m_{CO_{2}}}{M_{CO_{2}}}\\&\Rightarrow& m_{C}=m_{CO_{2}}\dfrac{M_{C}}{M_{CO_{2}}}\\&=&2.7\times\dfrac{12}{44}\\&\Rightarrow& m_{C}=0.74\,g \end{array}$

 

$\begin{array}{lcl} m_{H}&=&m_{H_{2}O}\dfrac{2M_{H}}{M_{H_{2}O}}\\&=&1.1\times\dfrac{2\times 1.0}{18}\\&\Rightarrow& m_{H}=0.12\,g \end{array}$

 

$\begin{array}{lcl} m_{O}&=&m-\left(m_{C}+m_{H}\right)\\&=&1.35-(0.74+0.12)\\&\Rightarrow& m_{O}=0.49\,g \end{array}$

 

2) a) Pourcentage massique centésimal :

 

$-\ $ en carbone :

 

$\begin{array}{lcl} \%C&=&\dfrac{m_{C}\times 100}{m}\\&=&\dfrac{0.74\times 100}{1.35}\\&\Rightarrow& \%C=55 \end{array}$

 

$-\ $ en hydrogène :

 

$\begin{array}{lcl} \%H&=&\dfrac{m_{H}\times 100}{m}\\&=&\dfrac{0.12\times 100}{1.35}\\&\Rightarrow& \%H=9.0 \end{array}$

 

$-\ $ en oxygène :

 

$\begin{array}{lcl} \%O&=&\dfrac{m_{O}\times 100}{m}\\&=&\dfrac{0.49\times 100}{1.35}\\&\Rightarrow& \%C=36 \end{array}$

 

b) Montrons que la formule de $A$ est $C_{4}H_{8}O_{2}$ 

 

Soit $C_{x}H_{y}O_{z}$ le composé $A$

 

$\begin{array}{lcl} \dfrac{12x}{\%C}&=&\dfrac{y}{\%H}\\&=&\dfrac{16z}{\%O}\\&=&\dfrac{M}{100}\\&\Rightarrow& x=\dfrac{\%C\times M}{12\times 100}\\&=&\dfrac{55\times 88}{12\times 100}\\&\Rightarrow& x=4 \end{array}$

 

$\begin{array}{lcl}\text{Par analogie }y&=&\dfrac{\%H\times M}{1.0\times 100}\\&=&\dfrac{9.0\times 88}{1.0\times 100}\\&\Rightarrow& y=8 \end{array}$

 

$\begin{array}{lcl}z&=&\dfrac{\%O\times M}{16\times 100}\\&=&\dfrac{36\times 88}{16\times 100}\\&\Rightarrow& z=2 \end{array}$

 

D'où la formule brute : $C_{4}H_{8}O_{2}$

 

3) a) Un acide est une entité chimique capable de céder au moins un proton.

 

b)  Équation chimique de la réaction de l'acide dans l'eau

 

$C_{3}H_{7}COOH+H_{2}O\ \rightarrow\ C_{3}H_{7}COO^{-}+H_{3}O^{+}$

 

c) les couples acide-base mis en jeu sont :

 

$H_{3}O^{+}|H_{2}O\text{ et }C_{3}H_{7}COOH|C_{3}H_{7}COO^{-}$

 

d) concentration molaire $C$ de la solution

 

$\begin{array}{lcl} C&=&\dfrac{n}{V}\\&=&\dfrac{0.1}{500\cdot 10^{-3}}\\&\Rightarrow& C=0.2\,mol\cdot L^{-1} \end{array}$

1) Masse de cristaux à peser pour préparer $S_{o}$

 

$\begin{array}{lcl} m&=&n\times M\\&=&C\times V\times M\\&=&0.1\times 100\cdot 10^{-3}\times(12\times 6+6\times 1.0+2\times 16)\\&\Rightarrow& m=1.1\,g \end{array}$

 

2) a) Équation bilan de la réaction de l'acide benzoique avec l'eau

 

$C_{6}H_{5}COOH+H_{2}O\ \rightarrow\ C_{6}H_{5}COO^{-}+H_{3}O^{+}$

 

Montrons que l'acide benzoique n'est pas un acide fort

 

Pour un acide fort, $pH=-\log\,C$

 

$-\log\,C_{0}=-\log\,0.1=-\log\,10^{-1}=1\neq\,pH(pH=2.6)$

 

L'acide benzoique n'est pas un acide fort.

 

b) Détermination du coefficient de dissociation

 

Electroneutralité de la solution : $\left[H_{3}O^{+}\right]=\left[HO^{-}\right]+\left[C_{6}H_{5}COO^{-}\right]$, solution acide on néglige les ions $HO^{-}$ devant les ions $H_{3}O^{+}\Rightarrow\left[C_{6}H_{5}COO^{-}\right]=\left[H_{3}O^{+}\right]=10^{-pH}$

 

$\begin{array}{lcl} \alpha_{0}&=&\dfrac{\left[C_{6}H_{5}COO^{-}\right]}{C_{0}}\\&=&\dfrac{10^{-pH}}{C_{0}}\\&=&\dfrac{10^{-2.6}}{0.1}\\&\Rightarrow&\alpha_{0}=0.025 \end{array}$

 

3) Le coefficient $\alpha_{1}$ de l'acide dans la solution $S_{1}$

 

$\begin{array}{lcl} \alpha_{1}&=&\dfrac{\left[C_{6}H_{5}COO^{-}\right]}{C_{1}}\\&=&\dfrac{10^{-pH}}{\dfrac{C_{0}}{10}}\\&=&\dfrac{10^{1}\times 10^{-pH}}{C_{0}}\\&=&\dfrac{10^{-pH+1}}{C_{0}}\\&=&\dfrac{10^{-3.1+1}}{0.1}\\&\Rightarrow&\alpha_{1}=0.079 \end{array}$

On remarque que $\alpha_{1}>\alpha_{0}$ donc la dissociation augmente avec la dilution

1) a) Si l'acide benzoique était un acide fort, il réagirait totalement avec l'eau. 

 

Pour une solution de concentration $c=1.0\cdot 10^{-2}mol\cdot L^{-1}\;,\ \left[H_{3}O^{+}\right]=c.$

 

Ici le $pH$ est égale à $3.1$ donc $\left[H_{3}O^{+}\right]=10^{-3.1}mol\cdot L^{-1}=7.9\cdot 10^{-4}mol\cdot L^{-1}\;,\ \left[H_{3}O^{+}\right]\neq c$

 

L'acide benzoique est un acide faible.

 

1) b) $C_{6}H_{5}COOH+H_{2}O\leftrightarrows C_{6}H_{5}COO^{-}+H_{3}O^{+}$

 

$K_{a}=\dfrac{\left[H_{3}O^{+}\right]\left[C_{6}H_{5}COO^{-}\right]}{\left[C_{6}H_{5}COOH\right]}$

 

2)a) Pour une base forte $pH=14+\log\,C$

 

Pour l'ion benzoate est une base faible.

 

2) b) $C_{6}H_{5}COO^{-}+H_{2}O\leftrightarrows C_{6}H_{5}COOH+HO^{-}$

 

$K_{R}=\dfrac{\left[HO^{-}\right]\left[C_{6}H_{5}COOH\right]}{\left[C_{6}H_{5}COO^{-}\right]}=\dfrac{K_{e}}{K_{a}}=1.6\cdot 10^{-10}$

 

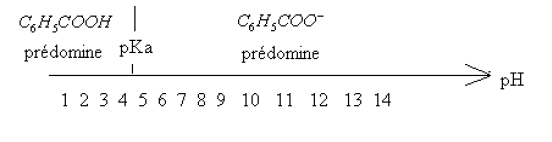
3) a) $pH>pK_{a}$ donc la base du couple prédomine :

 

3) b)

 

 

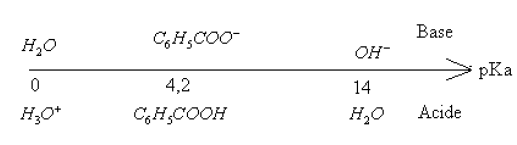
3) c) $C_{6}H_{5}COOH+HO^{-}\longrightarrow\ C_{6}H_{5}COO^{-}+H_{2}O$

 

$$K_{R}=\dfrac{\left[C_{6}H_{5}COO^{-}\right]}{\left[C_{6}H_{5}COOH\right]\left[HO^{-}\right]}=\dfrac{K_{a}}{K_{e}}$$

 

$K_{R}=10^{14-4.2}=6.3\cdot 10^{9}>10^{4}$

 

La constance de réaction est très grande: la réaction peut être considérée comme totale.

 

4) La quantité initiale de chaque espèce n'est pas modifiée lors du mélange. 

 

Les deux solution $S_{1}$ et $S_{2}$ ont la même concentration et on en prélève le même volume ; l'acide benzoique et l'ion benzoate ont donc même concentration dans le mélange.

 

Comme $pH=pKa+\log\dfrac{B}{A}\;,\ \text{or }[B]=[A]\Rightarrow\,pH=pKa=4.2$

1) a) La formule brute d'un acide carboxylique est :

 

$C_{n}H_{2n+1}COOH\text{ ou }R-COOH$ 

 

Montrons que sa masse molaire s'écrit sous la forme : $M=14n+32$

 

$M=M_{C_{n}H_{2n}O_{2}}=12n+2n+2\times 16=14n+32$

 

b) Formule semi-développée et nom de chaque isomère

 

$M=88\,g\cdot mol^{-1}\Rightarrow 14n+32=88\Rightarrow n=4$

 

D'où $C_{3}H_{7}-COOH$ 

 

$CH_{3}-CH_{2}-CH_{2}-COOH$ : acide butanoique

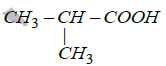  : acide $2-$methylpropanoique

                        

 

2) a) La réaction est une réaction d'oxydation

 

b) Formule semi-développée, nom et classe de l'alcool

 

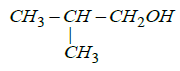    : $2-\text{methylpropan}-1-\text{ol}$

                           

 

Classe : alcool primaire

 

3) a) La réaction est une réaction d'estérification directe

 

b) équation chimique de la réaction

 

 

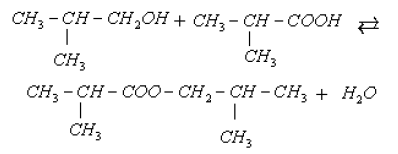
d) Nom de l'ester formé :

 

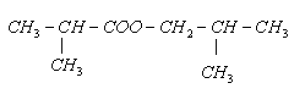 $2-\text{méthylpropate}-2-\text{méthylpropyle}$

                             

                              

4) a) Calcule de la masse $m$

 

$\begin{array}{lcl} m&=&n\times M\\&=& CV\times M\\&=&0.01\times 100\cdot 10^{-3}\times 88\\&\Rightarrow&\boxed{m=88\,mg} \end{array}$

 

b) Calcule de la concentration en ion $H_{3}O^{+}$

 

$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&10^{-pH}\\&=&10^{-3.9}\\&\Rightarrow&\left[H_{3}O^{+}\right]=1.3\cdot 10^{-4}mol\cdot L^{-1} \end{array}$

 

Pour un acide fort, $pH=-\log\,C$

 

$-\log\,C=-\log\,0.01=2\neq\,pH(pH=3.9)$

 

L'acide est donc un acide faible

 

c) Équation de dissociation de l'acide $A$ dans l'eau

 

$C_{3}H_{7}COOH+H_{2}O\ \rightarrow\ C_{3}H_{7}COO^{-}+H_{3}O^{+}$

1) a) Montrons que le méthylamine est une base alors que $B$ est une base forte.

 

Pour une base forte

 

$pH=14+\log\,C$

 

Solution $S_{1}$

 

$-\ $ sans dilution : $pH_{1}=14+\log\,C_{1}=11.85$

 

$\begin{array}{lcl}-\ \text{Avec dilution : }pH_{1}&=&14+\log\dfrac{C_{1}}{10}\\&=&14+\log\,C_{1}-1\\&=&11.85-1\\&=&10.85\neq\,pH_{1}\left(pH_{1}=11.35\right) \end{array}$

 

Dans le méthylamine est une base faible.

 

Solution $S_{2}$ :

 

$-\ $ Sans dilution : $pH_{2}=14+\log\,C_{2}=12$

 

$\begin{array}{lcl}-\ \text{Avec dilution : }pH_{2}&=&14+\log\dfrac{C_{2}}{10}\\&=&14+\log\,C_{2}-1\\&=&12-1\\&=&11\\&=&pH_{2} \end{array}$

 

$B$ est donc une base forte.

 

b) Calcule de la concentration $C_{2}$

 

$\begin{array}{lcl} pH_{2}&=&14+\log\,C_{2}\\&\Rightarrow& C_{2}=10^{pH_{2}-14}\\&=&10^{12-14}\\&\Rightarrow&\boxed{C_{2}=10^{-2}mol\cdot L^{-1}} \end{array}$

 

c) Préparation de la solution

 

2) Établissement de la relation $pH=\dfrac{1}{2}(pKa+pKe+\log\,C)$ vérifiée par la solution $S_{1}.$

 

Espèces chimiques en solution :

 

$H_{3}O^{+}\ ;\ HO^{+}\ ;\ CH_{3}NH_{2}\ ;\ CH_{3}NH_{3}^{+}\ ;\ H_{2}O$

 

Electroneutralité de la solution :

 

$\left[H_{3}O^{+}\right]+\left[CH_{3}NH_{3}^{+}\right]=\left[HO^{-}\right]$

 

$\left[HO^{-}\right]>>\left[H_{3}O^{+}\right]$ (Solution basique)

 

$\Rightarrow\left[CH_{3}NH_{3}^{+}\right]=\left[HO^{-}\right]=\dfrac{K_{e}}{\left[H_{3}O^{+}\right]}$

 

Conservation de la matière :

 

$\left[CH_{3}NH_{3}^{+}\right]+\left[CH_{3}NH_{2}\right]=C$ la base faible se dissocie faiblement

 

$\Rightarrow\left[CH_{3}NH_{2}\right]=C$

 

$\begin{array}{lcl} K_{a}&=&\dfrac{\left[CH_{3}NH_{2}\right]\left[H_{3}O^{+}\right]}{\left[CH_{3}NH_{3}^{+}\right]}\\&=&\dfrac{C\left[H_{3}O^{+}\right]}{\dfrac{K_{e}} {\left[H_{3}O^{+}\right]}}\\&=&\dfrac{C\left[H_{3}O^{+}\right]^{2}}{K_{e}}\\&\Rightarrow&\left[H_{3}O^{+}\right]^{2}=\dfrac{K_{a}\times K_{e}}{C}\\&\Rightarrow&-\log\left[H_{3}O^{+}\right]^{2}=-\log\dfrac{1}{C}\\&\Rightarrow&2pH=pK_{a}+pK_{e}+\log\,C\\&\Rightarrow& pH=\dfrac{1}{2}\left(pK_{a}+pK_{e}+\log\,C\right) \end{array}$

 

3) Valeur du $pK_{a}$

 

Pour $\log\,C=0$ on a $pH=\dfrac{1}{2}\left(pK_{a}+pK_{e}\right)$

 

$\Rightarrow pK_{a}=2pH-pK_{e}$

 

$pK_{a}=2\times 12.35-14=10.7$

 

Concentration de la solution

 

$\begin{array}{lcl}pH&=&\dfrac{1}{2}\left(pK_{a}+pK_{e}+\log\,C\right)\\&\Rightarrow&\log\,C=2pH\left(pK_{a}+pK_{e}\right)\\&\Rightarrow&C=10^{2pH\left(pK_{a}+pK_{e}\right)}\\&=&10^{2\times10.85(10.7+14)}\\&\Rightarrow&C=10^{-3}mol\cdot L^{-1} \end{array}$

1) a) Un acide est fort, s'il s'ionise totalement dans l'eau.

 

Un acide est faible s'il s'ionise partiellement dans l'eau.

 

b) Pour un acide fort $pH=-\log\,C$

 

Pour une même concentration $C=10^{-2}mol/L\ ;\ pH=-\log\,10^{-2}=2.$

 

Donc on peut conclure que $A_{2}H$ est un acide fort et $A_{1}H$ ; $A_{3}H$ et $A_{4}H$ sont des acides faibles.

 

2) a) Calcule des coefficients de dissociation pour chaque acide faible

 

$AH\ +\ H_{2}O\ \leftrightarrows\ A^{-}\ +\ H_{3}O^{+}$

 

$\alpha=\dfrac{[AH]_{d}}{[AH]_{i}}=\dfrac{[A^{-}]}{C}=\dfrac{\left[H_{3}O^{+}\right]}{C}=\dfrac{10^{-pH}}{C}$

 

$\left\lbrace\begin{array}{lcl} d&:&\text{dissocié}\\ i&:&\text{initial}\end{array}\right.$

 

$\alpha_{1}=\dfrac{10^{-3.4}}{10^{-2}}\Rightarrow\alpha_{1}=0.039$,

 

$\alpha_{3}=\dfrac{10^{-5.6}}{10^{-2}}\Rightarrow\alpha_{3}=0.25\cdot 10^{-3}$,

 

$\alpha_{4}=\dfrac{10^{-2.9}}{10^{-2}}\Rightarrow\alpha_{4}=0.13$

 

$\alpha_{4}>\alpha_{1}>\alpha_{3}.$

 

La force de l'acide croit avec le coefficient de dissociation ; d'où le classement :

 

 

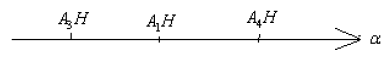
b) Relation entre la constante d'acide $K_{a}$ et le coefficient de dissociation $\alpha$

 

 

 

 

$\alpha=\dfrac{x}{C}\Rightarrow x=\alpha\times C$

 

$\begin{array}{lcl} K_{a}&=&\dfrac{\left[H_{3}O^{+}\right][A^{-}]}{[AH]}\\&=&\dfrac{x\times x}{C-x}\\&=&\dfrac{\alpha C\times\alpha C}{C-\alpha\times C}\\&=&C\dfrac{\alpha^{2}}{1-\alpha} \end{array}$

 

c) Calcule de la constante d'acide de chaque acide faible

 

$K_{\alpha_{1}}=C\dfrac{\alpha_{1}^{2}}{1-\alpha_{1}}=10^{-2}\dfrac{0.039^{2}}{1-0.039}=1.6\cdot10^{-5}$,

 

$K_{\alpha_{3}}=C\dfrac{\alpha_{3}^{2}}{1-\alpha_{13}}=10^{-2}\dfrac{\left(0.25\cdot 10^{-3}\right)^{2}}{1-0.25\cdot 10^{-3}}=6.3\cdot10^{-10}$,

 

$K_{\alpha_{4}}=C\dfrac{\alpha_{4}^{2}}{1-\alpha_{4}}=10^{-2}\dfrac{(0.13)^{2}}{1-0.13}=1.9\cdot10^{-4}$,

 

$K_{\alpha_{4}}>K_{\alpha_{1}}>K_{\alpha_{3}}.$

 

La force de l'acide croit avec la constante de dissociation d'ou le classement :

 

 

5) La nouvelle valeur du coefficient de dissociation de $A_{1}H$

 

$\begin{array}{lcl} \alpha_{1}&=&\dfrac{10^{-pH}}{C'}\\&=&\dfrac{10^{-pH}}{\dfrac{C}{10}}\\&=&\dfrac{10^{-pH+1}}{C}\\&=&\dfrac{10^{-3.9+1}}{10^{-10}}\\&=&0.13 \end{array}$

 

$\alpha_{1}>\alpha_{1}.$

 

La dilution a pour effet de déplacer l'équilibre chimique dans le sens de la dissociation de l'acide.