Solution des exercices : Amplificateur opérationnel : montages dérivateur et intégrateur 1er S
Classe:
Première
Exercice 1.
1. Représentation symbolique d'un amplificateur opérationnel idéal
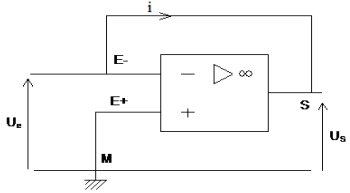
2. Identification de ces montages
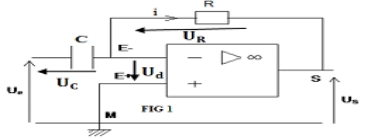
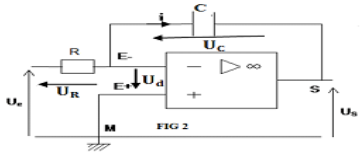
La loi d'additivité des tensions s'écrit :
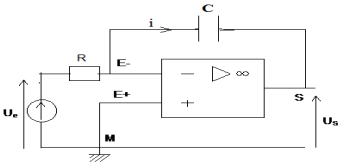
$-\ $Pour le premier montages (fig 1) :
$\begin{array}{rcl} U_{e}&=&U_{c}-U_{d}\\\Rightarrow\;U_{e}&=&\dfrac{q}{C}-0\\\Rightarrow\;q&=&CU_{e}\\\Rightarrow\dfrac{dq}{dt}&=&\dfrac{d}{dt}\left(CU_{e}\right)\\\Rightarrow\;i&=&C\dfrac{dU_{e}}{dt}\quad(1) \end{array}$
$\begin{array}{rcl} U_{S}&=&-U_{R}-U_{d}\\\Rightarrow\;U_{S}&=&-Ri-0\\\Rightarrow\;U_{S}&=&-Ri\quad(2)\ ;\\(1)\text{ et }\quad(2)\Rightarrow\;U_{S}&=&-RC\dfrac{dU_{e}}{dt} \end{array}$
La tension de sortie est proportionnelle à l'opposée de la dérivée par rapport au temps de la tension d'entrée.
Le montage est donc un montage dérivateur
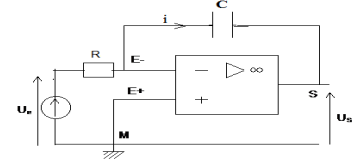
$-\ $Pour le deuxième montage (fig2) :
$\begin{array}{rcl} U_{e}&=&U_{R}-U_{d}\\\Rightarrow\;U_{d}\\\Rightarrow\;U_{e}&=&Ri\\\Rightarrow\;i&=&\dfrac{U_{e}}{R}\quad(1) \end{array}$
$$\begin{array}{rcl} U_{S}&=&-U_{c}-U_{d}\\\Rightarrow\;U_{S}&=&-\dfrac{q}{C}-\dfrac{q}{C}-0\\\Rightarrow\;U_{S}&=&-\dfrac{q}{C}\quad(2)\\\text{ or }q&=&\int\,idt\text{ et }i\\&=&\dfrac{U_{e}}{R}\quad(1)\\\Rightarrow\;q&=&\int\dfrac{U_{e}}{R}dt\text{ dans }\quad\\\Rightarrow\;U_{S}&=&-\dfrac{1}{RC}\int\,U_{e}dt \end{array}$$
La tension de sortie est proportionnelle à l'opposé de l'intégral par rapport au temps de la tension d'entrée.
Le montage est donc un montage intégrateur
Exercice 2
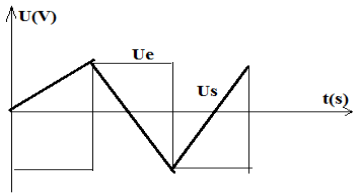
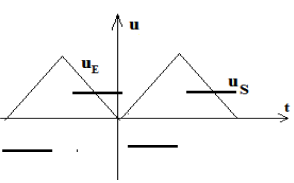
1. Représentation, sur de papier millimétrique, des variations de la tension $U_{e}$ en et de la tension $U_{s}$ à la sortie
Le montage est un montage dérivateur qui transforme la tension triangulaire de la forme $U_{e}=at+b$ en tension carrée de la forme $U_{S}=a$
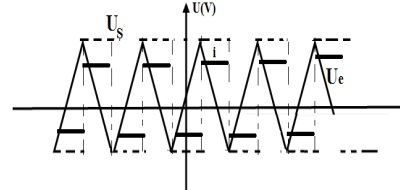
2. Représentation des variations de l'intensité du courant dans le résistor (Voir figure)
$\begin{array}{rcl} U_{S}&=&R_{S}i\\\Rightarrow\;i&=&\dfrac{U_{S}}{R_{S}} \end{array}$
Les variations de l'intensité du courant i correspondent aux variations de la tension de sortie $U_{S}$ à une constante prés
Exercice 3
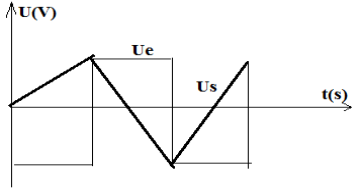
Représentation de la tension de sortie US(voir figure)
Ce montage est un montage intégrateur qui transforme une tension d'entrée $U_{e}$ carrée en tension de sortie $U_{S}$ triangulaire
$\begin{array}{rcl} \Rightarrow\;U_{S}&=&\dfrac{1}{RC}\int\,U_{e}dt \end{array}$
Exercice 4
1. Schéma d'un montage intégrateur
2. Représentation graphique des variations de $U_{S}(t)$
Exercice 5
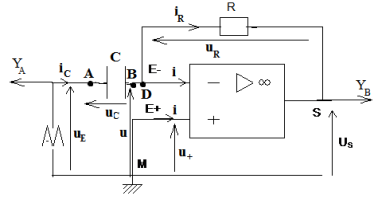
1.1 En appliquant la loi des nœuds en $D$, montons $i_{R}=i_{C}$
La loi des nœuds en $D$ s'écrit :
$\begin{array}{rcl} i_{C}&=&i_{R}+i_{-}\\\text{ or }i_{-}&=&0\\\Rightarrow\;i_{C}{R}&=&i_{C} \end{array}$
1.2. Exprimons $i_{R}$ en fonction de
$\begin{array}{rcl} i_{R}&=&i_{C}\\\text{ or }i_{C}&=&\dfrac{dq}{dt}\\\Rightarrow\;i_{R}&=&\dfrac{dq}{dt} \end{array}$
Déduction de l'expression liant $i_{R}$ à $u_{C}$ et à $C$
$\begin{array}{rcl} i_{R}&=&i_{C}\\\text{ or }\,q&=&Cu_{c}\\\Rightarrow\;i_{R}&=&\dfrac{d\left(Cu_{c}\right)}{dt}\\\Rightarrow\;i_{R}&=&C\dfrac{du_{c}}{dt} \end{array}$
1.3. En appliquant la loi des tensions, établissons que $u_{c}=-u_{R}$ et que $u_{E}=u_{c}$
La loi d'additivité des tensions :
$\begin{array}{rcl} u_{S}+u_{R}+u_{E^{+}E^{-}}+u_{+}&=&0\\\text{ or }u_{E^{+}E^{-}}&=&0\\\Rightarrow\;u_{S}&=&-u_{R} \end{array}$
$\begin{array}{rcl} u_{E}&=&u_{c}+u_{-}\\\text{ or }u_{-}&=&0\\\Rightarrow\;u_{E}&=&u_{C} \end{array}$
1.4 Expression de $u_{s}$ en fonction de $R$, $C$ et $\dfrac{du_{c}}{dt}$
$\begin{array}{rcl} u_{S}&=&-u_{R}\\&=&-Ri_{R}\\\text{ or }i_{R}&=&C\dfrac{du_{c}}{dt}\\\Rightarrow\;u_{s}&=&-RC\dfrac{du_{c}}{dt} \end{array}$
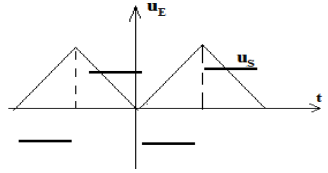
2. Oscillogramme obtenu en voie $B$
$\begin{array}{rcl} u_{s}&=&-RC\dfrac{du_{c}}{dt}\\\text{ or }u_{E}&=&u_{c}\\\Rightarrow\;u_{s}&=&-RC\dfrac{du_{E}}{dt} \end{array}$
Le montage est un montage dérivateur qui transforme la tension triangulaire de la forme $U_{e}=at+b$ en tension carrée de la forme $U_{s}=a$
3 Les caractéristiques de la tension de sortie $u_{s}$
$\begin{array}{rcl} u_{s}&=&-RC\dfrac{du_{E}}{dt}\\\text{ or }u_{E}&=&u_{Em}\cos\left(2\pi Nt\right)\\\Rightarrow\;u_{s}&=&2\pi NRCu_{Em}\sin\left(2\pi Nt\right) \end{array}$
La tension de sortie $u_{s}$ est une fonction sinusoidale du temps d'amplitude : $u_{sm}=2\pi NRCu_{Em}$ : de pulsation :
$\alpha=2\pi N$ et de fréquence $N$
Oscillogrammes obtenus en voie $A$ et en voie $B\cdot A$ l'origine des dates , le spot est à gauche de l'écran
Exercice 6
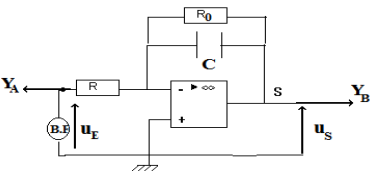
Soit le montage de la figure $1$
$L'A\cdot O$ est considéré comme idéal
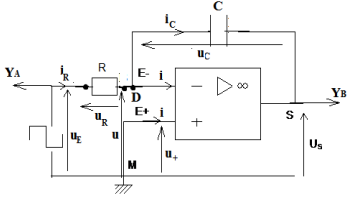
1. Afin d'établir une relation entre $\dfrac{du_{s}}{dt}$ et $u_{E}$
1.1. Appliquons la loi des nœuds en $D$ et montrons que $i_{c}=i_{R}$
La loi des nœuds en $D$ s'écrit :
$\begin{array}{rcl}i_{c}&=&i_{R}+i_{-}\\\text{ or }i_{-}&=&0\\\Rightarrow\;i_{R}&=&i_{c}\end{array}$
1.2. Expression de $i_{R}$ en fonction de $\dfrac{dq}{dt}$
$i_{R}=\dfrac{dq}{dt}$
Déduction d'une relation entre $i_{R}$, $\dfrac{du_{c}}{dt}$ et $C$
$\begin{array}{rcl} i_{R}&=&\dfrac{dq}{dt}\\\text{ or }q&=&Cu_{c}\\\Rightarrow\,i_{R}&=&\dfrac{d\left(Cu_{c}\right)}{dt}\\\Rightarrow\;i_{R}&=&C\dfrac{du_{c}}{dt} \end{array}$
1.3. En appliquant la loi des tensions, établissons que
$\begin{array}{rcl} u_{s}&=&-u_{c}\text{ et que }u_{R}=u_{E} \end{array}$
$\begin{array}{rcl} u_{S}+u_{C}+u_{E^{+}E^{-}} +u_{+}&=&0\\\text{ or }u_{E^{+}E^{-}}&=&u_{+}\\&=&0\\\Rightarrow\;u_{S}&=&-u_{C} \end{array}$
$\begin{array}{rcl} u_{E}&=&u_{R}+u_{-}\\\text{ or }u_{-}&=&0\\\Rightarrow\;u_{R}&=&u_{E} \end{array}$
1.4. A partir de la relation établie $1\cdot 2\cdot$ et des relations précédentes, en appliquant la loi d’Ohm au conducteur
ohmique, exprimer $\dfrac{du_{s}}{dt}$ en fonction de $R$, $C$ et $u_{E}$
$\begin{array}{rcl} u_{s}&=&-u_{c}\\\Rightarrow\dfrac{du_{s}}{dt}&=&\dfrac{du_{c}}{dt}\\\text{ or }i_{R}&=&C\dfrac{du_{c}}{dt}\\\text{ et }u_{R}&=&Ri_{R}=u_{E}\\\Rightarrow\;i_{R}&=&\dfrac{u_{E}}{R}\\\Rightarrow\;C\dfrac{du_{c}}{dt}&=&\dfrac{u_{E}}{R}\\\Rightarrow\dfrac{du_{c}}{dt}&=&\dfrac{u_{E}}{RC}\\\Rightarrow\dfrac{du_{s}}{dt}&=&-\dfrac{u_{E}}{RC} \end{array}$
2. L'oscillographe électronique mesure en voie A la tension d'entrée $u_{E}$ et en voie $B$, la tension de sortie $u_{S}$
ci-dessous
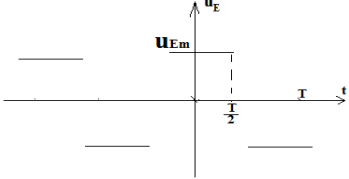
2.1. Montrons que sur l'intervalle de temps $t\in\left[0\,; \dfrac{T}{2}\right]$, $u_{s}$ peut se mettre sous la forme : $u_{s}=-\dfrac{1}{RC}u_{Em}t+b$ où $u_{Em}$ est la valeur maximale de $u_{E}$ et $b$ une constante
$\begin{array}{rcl} t\in\left[0\;,\dfrac{T}{2}\right]\;,u_{E}&=&u_{Em}\\\Rightarrow\dfrac{du_{s}}{dt}&=&-\dfrac{u_{Em}}{RC}\\\Rightarrow\;u_{S}&=&-\dfrac{1}{RC}u_{Em}t+b \end{array}$
2.2. Montrons que sur l'intervalle de temps : $t\in[0\;,\dfrac{T}{2}]$, $u_{s}$ peut se mettre sous la forme : $u_{s}=\dfrac{1}{RC}u_{Em}t+c$ où $c$ est une constante
$\begin{array}{rcl} t\in(\dfrac{T}{2})&=&\dfrac{1}{RC}u_{Em}\dfrac{T}{2}+c\\&=&-\dfrac{1}{RC}u_{Em}\dfrac{T}{2}+b\cdot\\\text{ Pour } b&=&0\\\Rightarrow\;C&=&-\dfrac{2}{RC}u_{Em}\dfrac{T}{2}\\\Rightarrow\;u_{s}(t)&=&-\dfrac{1}{RC}u_{Em}(t+T) \end{array}$
2.4. Déduction de l'étude précédente, l'oscillogramme obtenu en voie $B;$ (Voir figure)
3.1. Montrons que la valeur instantanée de la tension de sortie uS peut se mettre sous la forme :
$u_{s}=U_{Sm}\sin(2\pi Nt)+d$
$$\begin{array}{rcl} U_{s}&=&-\dfrac{1}{RC}\int u_{E}dt\\\text{ or }u_{E}&=&-u_{Em}\cos(2\pi Nt)\\\Rightarrow\;U_{S}&=&\dfrac{1}{RC}\int u_{Em}\cos(2\pi Nt)dt
\\\Rightarrow\;U_{S}&=&-\dfrac{1}{2\pi NRC}u_{Em}\cos(2\pi Nt)+d\\\Rightarrow\;U_{s}1+1 U_{Sm}\cos(2\pi Nt)+d\\\Rightarrow\;U_{Sm}&=&\dfrac{1}{2\pi NRC}U_{Em} \end{array}$$
\\\Rightarrow\;U_{S}&=&-\dfrac{1}{2\pi NRC}u_{Em}\cos(2\pi Nt)+d\\\Rightarrow\;U_{s}1+1 U_{Sm}\cos(2\pi Nt)+d\\\Rightarrow\;U_{Sm}&=&\dfrac{1}{2\pi NRC}U_{Em} \end{array}$$
$U_{Sm}$ est la valeur maximale de la tension de sortie, d est une constante
Calcul de $U_{Sm}.$
En supposant qu'à $t=0$, $u_{s}=0$,
$\begin{array}{rcl} U_{Sm}&=&\dfrac{1}{2\pi \times 50\times 10\cdot10^{3}1.0\cdot10^{-6}}\times6.0\\\Rightarrow\;U_{Sm}&=&1.9\,V \end{array}$
Calcul de $d$
$\begin{array}{rcl} U_{x}(0)&=&-\dfrac{1}{2\pi NCR}u_{Em}\cos(2\pi N\times 0)+d\\&=&0\\\Rightarrow-\dfrac{1}{2\pi NRC}U_{Em}+d&=&0\\\Rightarrow\;d&=&\dfrac{1}{2\pi NRC}U_{Em}\\\Rightarrow\;d&=&1.9\,V \end{array}$
2.2. Oscillogrammes obtenus en voie $A$ et en voie $B$
Exercice 7
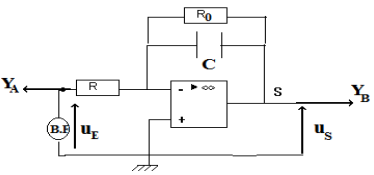
1. Rappel de l'expression qui lie $\dfrac{du_{E}}{dt}$, $R$, $C$, et $u_{S}$
$\begin{array}{rcl} u_{S}+u_{R}+u_{E^{+}E^{-}}+u^{+}&=&0\\\Rightarrow\;u_{S}+u_{R}+0+0&=&0\\\Rightarrow\;u_{S}&=&-u_{R}\\\Rightarrow\;u_{S}&=&-Ri_{R}\quad(1) \end{array}$
$\begin{array}{rcl} u_{E}+u_{C}+U^{-}&=&0\\\Rightarrow\;u_{E}&=&+u_{C}+0\\&=&0\\\Rightarrow\;u_{C}&=&-u_{E}\\\text{ or }i_{R}&=&\dfrac{dq}{dt}\\&=&\dfrac{dCu_{c}}{dt}\\&=&C\dfrac{du_{c}}{dt}\\&=&C\dfrac{du_{c}}{dt}\\\Rightarrow\;i_{R}&=&-C\dfrac{du_{E}}{dt}\quad (2) \end{array}$
$\begin{array}{rcl} (1)\text{ et }(2)&\Rightarrow&\;u_{s}\\&=&-RC\dfrac{du_{E}}{dt} \end{array}$
2. Oscillogramme obtenu (Voir figure)
Un montage à amplificateur opérationnel est en mode linéaire s'il est rebouclé sur l'entrée inverseuse de l'amplificateur opérationnel (montage en contre réaction)

Commentaires
Harouna Kaboré (non vérifié)
mar, 02/04/2025 - 18:36
Permalien
Correction
Ajouter un commentaire