Solution des exercices : Association de conducteurs ohmiques 3e
Classe:
Troisième
Exercice 1
Complétons le tableau
$$\begin{array}{|c|c|c|c|}\hline R_{1}&R_{2}&R_{e}&\text{Types} \\(\text{en }\Omega)&(\text{en }\Omega)&(\text{en }\Omega)&\text{d'association} \\ \hline 680&820&1500&\text{Série} \\ \hline 39.53&68&25&\text{Parallèle} \\ \hline 470&33&503&\text{Série} \\ \hline 51&46&24.985&\text{Parallèle} \\ \hline 56&56&28&\text{Parallèle} \\ \hline\end{array}$$
Exercice 2
Nous disposons de deux lots de résistances $R_{1}\ $ et $\ R_{2}$ telles que $R_{1}=33\;\Omega\ $ et $\ R_{2}=47\;\Omega.$ Indiquons, en précisant le type d'association, le nombre de résistances de chaque que nous utilisons :
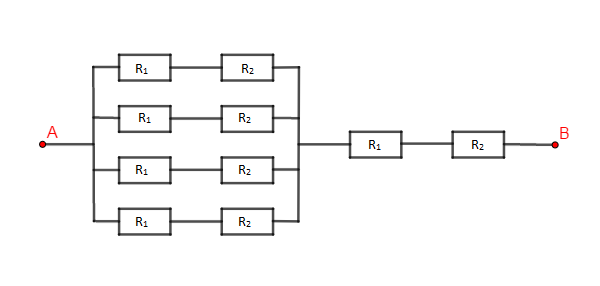
1) Pour avoir une résistance équivalente $R_{AB}$ de $100\;\Omega$, nous allons utiliser le type d'association ci-dessous

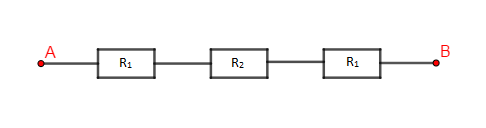
2) Pour avoir une résistance équivalente $R_{AB}$ de $113\;\Omega$, nous pouvons utiliser le type d'association ci-dessous

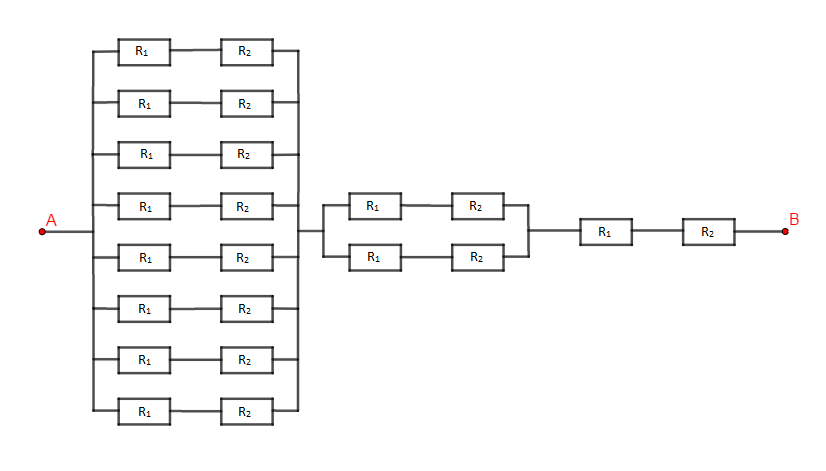
3) Pour avoir une résistance équivalente $R_{AB}$ de $130\;\Omega$, nous allons utiliser le type d'association ci-dessous

Exercice 3
1) $R_{1}=22\;\Omega$ et $R_{2}=33\;\Omega$ montées en série, trouvons la résistance équivalente
On a : $R_{e}=R_{1}+R_{2}$
A.N : $R_{e}=22+33=55$
Donc, $$\boxed{R_{e}=55\;\Omega}$$
2) $R_{1}=22\;\Omega$ et $R_{2}=33\;\Omega$ montées en parallèle, trouvons alors la résistance équivalente
On a : $\dfrac{1}{R_{e}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}$
Donc, $\dfrac{1}{R_{e}}=\dfrac{R_{2}+R_{1}}{R_{1}.R_{2}}$
D'où, $R_{e}=\dfrac{R_{1}.R_{2}}{R_{1}+R_{2}}$
A.N : $R_{e}=\dfrac{22\times 33}{22+33}=13.2$
Ainsi, $$\boxed{R_{e}=13.2\;\Omega}$$
Exercice 4
Pour que la résistance du groupement obtenu soit de $11\;\Omega$ il faudra associer les conducteurs en parallèle. Plus précisément, si on met trois conducteurs identiques de résistance $33\;\Omega$ en parallèle on obtient une résistance équivalente de $11\;\Omega.$
En effet, on a : $\dfrac{1}{R_{e}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}$
Or, $R_{1}=R_{2}=R_{3}=33\;\Omega$
Donc, $\dfrac{1}{R_{e}}=\dfrac{1}{33}+\dfrac{1}{33}+\dfrac{1}{33}=\dfrac{3}{33}=\dfrac{1}{11}$
D'où, $R_{e}=11\;\Omega$
Exercice 5
1) Calculons la résistance $R_{2}$ du fil chauffant de cette lampe.
On a : $U=R_{2}I\ \Rightarrow\ R_{2}=\dfrac{U}{I}$
A.N : $R_{2}=\dfrac{4.5}{0.2}=22.5$
Donc, $$\boxed{R_{2}=22.5\;\Omega}$$
2) Trouvons la résistance équivalente à cette association.
On a : $\dfrac{1}{R_{e}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}$
Donc, $\dfrac{1}{R_{e}}=\dfrac{R_{2}+R_{1}}{R_{1}.R_{2}}$
D'où, $R_{e}=\dfrac{R_{1}.R_{2}}{R_{1}+R_{2}}$
A.N : $R_{e}=\dfrac{22.5\times 27}{22.5+27}=12.27$
Ainsi, $$\boxed{R_{e}=12.27\;\Omega}$$
Exercice 6
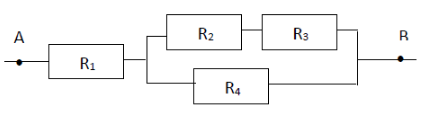
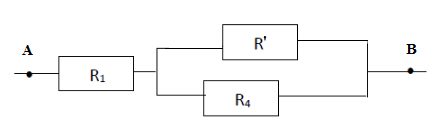
Soit le dipôle $AB$ constitué de conducteurs groupés comme indiqué dans le schéma suivant.
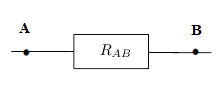
Trouvons la résistance équivalente du dipôle $AB$ ainsi obtenu sachant que
$$R_{1}=10\;\Omega\;;\ R_{2}=20\;\Omega\;;\ R_{3}=6\;\Omega\text{ et }R_{4}=9\;\Omega$$
$$R_{1}=10\;\Omega\;;\ R_{2}=20\;\Omega\;;\ R_{3}=6\;\Omega\text{ et }R_{4}=9\;\Omega$$

$R_{2}$ et $R_{3}$ sont montées en série donc soit $R'$ leur résistance équivalente.
On a : $R'=R_{2}+R_{3}$

Le groupement $(R_{2}\;,\ R_{3})$ ou encore $R'$ étant monté en parallèle avec $R_{4}$ alors, en considérant $R''$ comme la résistance équivalente, on aura :
$\dfrac{1}{R''}=\dfrac{1}{R'}+\dfrac{1}{R_{4}}$
Donc, $\dfrac{1}{R''}=\dfrac{R_{4}+R'}{R'.R_{4}}$
D'où, $R''=\dfrac{(R_{2}+R_{3}).R_{4}}{(R_{2}+R_{3})+R_{4}}$

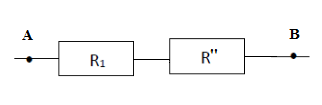
Enfin, le groupement $(R_{2}\;,\ R_{3}\;,\ R_{4})$ ou encore $R''$ étant monté en série avec $R_{1}$ alors, la résistance équivalente du dipôle $AB$ sera donnée par :
$$R_{AB}=R_{1}+R''$$
Or, $R''=\dfrac{(R_{2}+R_{3}).R_{4}}{(R_{2}+R_{3})+R_{4}}$
Donc, $R_{AB}=R_{1}+\dfrac{(R_{2}+R_{3}).R_{4}}{(R_{2}+R_{3})+R_{4}}=R_{1}+\dfrac{R_{4}(R_{2}+R_{3})}{R_{2}+R_{3}+R_{4}}$

Par suite,
$$R_{AB}=R_{1}+\dfrac{R_{4}(R_{2}+R_{3})}{R_{2}+R_{3}+R_{4}}$$
A.N : $R_{AB}=10+\dfrac{9(20+6)}{20+6+9}=16.685$
D'où, $$\boxed{R_{AB}=16.685\;\Omega}$$

Exercice 7
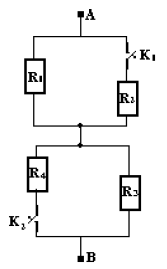
Des résistors de résistances respectives $R_{1}=12\;\Omega\;;\ R_{2}=R_{4}=6\;\Omega\ $ et $\ R_{3}=3\;\Omega$ sont groupés entre $A\ $ et $\ B$ comme indiqué par le schéma.

1) Trouvons la résistance du dipôle $AB$ ainsi constitué.
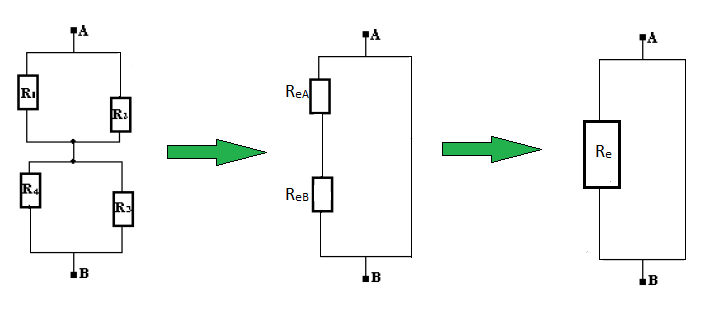
La configuration du dipôle $AB$ permet de constater que :
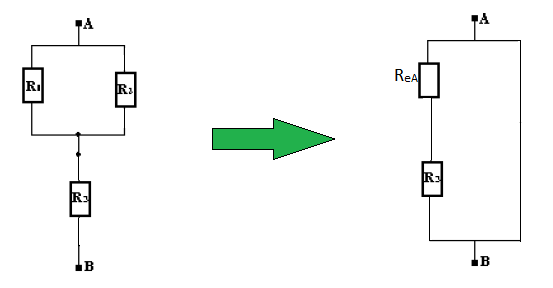
$-\ \ R_{_{1}}\ $ et $\ R_{_{2}}$ sont montées en parallèle
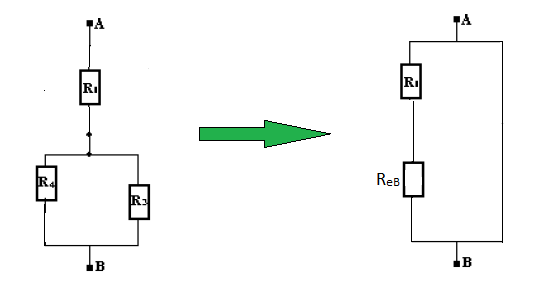
$-\ \ R_{_{3}}\ $ et $\ R_{_{4}}$ sont montées en parallèle
$-\ $ Les groupements $(R_{_{1}}\;,\ R_{_{2}})\ $ et $\ (R_{_{3}}\;,\ R_{_{4}})$ sont montés en série
Soient $R_{_{eA}}$ la résistance équivalente du groupement $(R_{_{1}}\;,\ R_{_{2}})\ $ et $\ R_{_{eB}}$ la résistance équivalente à l'association des résistances $R_{_{3}}\ $ et $\ R_{_{4}}$
On a alors : $\dfrac{1}{R_{_{eA}}}=\dfrac{1}{R_{_{1}}}+\dfrac{1}{R_{_{2}}}=\dfrac{R_{_{2}}+R_{_{1}}}{R_{_{1}}.R_{_{2}}}$
Donc, $R_{_{eA}}=\dfrac{R_{_{1}}.R_{_{2}}}{R_{_{1}}+R_{_{2}}}$
A.N : $R_{_{eA}}=\dfrac{12\times 6}{12+6}=\dfrac{72}{18}=4\;\Omega$
De la même manière : $\dfrac{1}{R_{_{eB}}}=\dfrac{1}{R_{_{3}}}+\dfrac{1}{R_{_{4}}}=\dfrac{R_{_{4}}+R_{_{3}}}{R_{_{3}}.R_{_{4}}}$
Donc, $R_{_{eB}}=\dfrac{R_{_{3}}.R_{_{4}}}{R_{_{3}}+R_{_{4}}}$
A.N : $R_{_{eB}}=\dfrac{3\times 6}{3+6}=\dfrac{18}{9}=2\;\Omega$
On obtient alors le schéma suivant :

Soit $R_{_{e}}$ la résistance du dipôle $AB$
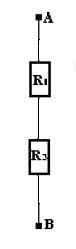
Comme $R_{_{eA}}\ $ et $\ R_{_{eB}}$ sont montées en série alors,
$$R_{_{e}}=R_{_{eA}}+R_{_{eB}}$$
A.N : $R_{_{e}}=4+2=6$
Ainsi,$$\boxed{R_{_{e}}=6\;\Omega}$$
2) A ce dipôle, on applique une tension de $6\;V$, déterminons l'intensité du courant débité par le générateur dans chacun des cas suivants.
a) Les interrupteurs $K_{1}\ $ et $\ K_{2}$ fermés.
Le circuit équivalent se présente comme suit :

D'après la loi d'Ohm, on a : $U_{_{AB}}=R_{_{e}}.I$
Donc, $I=\dfrac{U_{_{AB}}}{R_{_{e}}}$
A.N : $I=\dfrac{6}{6}=1$
D'où, $$\boxed{I=1\;A}$$
b) L'interrupteur $K_{1}$ fermé et l'interrupteur $K_{2}$ ouvert.
Donc, aucun courant ne traverse $R_{_{4}}$ et le circuit devient :

On constate que le groupement $(R_{_{1}}\;,\ R_{_{2}})$ est en série avec $R_{_{3}}$
Donc, d'après la loi d'Ohm : $U_{_{AB}}=(R_{_{eA}}+R_{_{3}}).I$
Par suite, $I=\dfrac{U_{_{AB}}}{R_{_{eA}}+R_{_{3}}}$
A.N : $I=\dfrac{6}{4+3}=\dfrac{6}{7}=0.857$
D'où, $$\boxed{I=0.857\;A}$$
c) l'interrupteur $K_{1}$ ouvert et L'interrupteur $K_{2}$ fermé
Donc, aucun courant ne traverse $R_{_{2}}$ et le circuit se présente comme suit :

Ainsi, le groupement $(R_{_{3}}\;,\ R_{_{4}})$ est en série avec $R_{_{1}}$
Alors, d'après la loi d'Ohm on a : $U_{_{AB}}=(R_{_{eB}}+R_{_{1}}).I$
Donc, $I=\dfrac{U_{_{AB}}}{R_{_{eB}}+R_{_{1}}}$
A.N : $I=\dfrac{6}{2+12}=\dfrac{6}{14}=0.428$
D'où, $$\boxed{I=0.428\;A}$$
d) Les interrupteurs $K_{1}\ $ et $\ K_{2}$ ouverts.
Aucun courant ne traverse $R_{_{2}}\ $ et $\ R_{_{4}}.$ On obtient alors le circuit suivant :

Ainsi, $R_{_{1}}\ $ et $\ R_{_{3}}$ sont en série.
Par suite, d'après la loi d'Ohm : $U_{_{AB}}=(R_{_{1}}+R_{_{3}}).I$
D'où, $I=\dfrac{U_{_{AB}}}{R_{_{1}}+R_{_{3}}}$
A.N : $I=\dfrac{6}{12+3}=\dfrac{6}{15}=0.4$
D'où, $$\boxed{I=0.4\;A}$$
3) Calculons les intensités $I_{_{1}}\;;\ I_{_{2}}\;;\ I_{_{3}}\ $ et $\ I_{_{4}}$ pour $K_{1}\ $ et $\ K_{2}$ fermés.
Lorsqu'on ferme $K_{1}\ $ et $\ K_{2}$, on obtient les relations suivantes sur les tensions :
$$U_{_{R_{1}}}=U_{_{R_{2}}}=U_{_{eA}}$$
$$U_{_{R_{3}}}=U_{_{R_{4}}}=U_{_{eB}}$$
Comme $U_{_{R_{1}}}=R_{_{1}}.I_{_{1}}\ $ et $\ U_{_{eA}}=R_{_{eA}}.I$ alors, $R_{_{1}}.I_{_{1}}=R_{_{eA}}.I$
Ce qui donne : $I_{_{1}}=\dfrac{R_{_{eA}}.I}{R_{_{1}}}$
A.N : $I_{_{1}}=\dfrac{4\times 1}{12}=\dfrac{4}{12}=0.333$
Donc, $$\boxed{I_{_{1}}=0.333\;A}$$
Pour déterminer $I_{_{2}}$, on applique la loi des nœuds :
$$I=I_{_{1}}+I_{_{2}}$$
Par suite, $I_{_{2}}=I-I_{_{1}}$
A.N : $I_{_{2}}=1-0.333=0.667$
Ainsi, $$\boxed{I_{_{2}}=0.667\;A}$$
De la même manière, d'après la loi d'Ohm, on a :
$$U_{_{R_{3}}}=R_{_{3}}.I_{_{3}}\ \text{ et }\ U_{_{eB}}=R_{_{eB}}.I$$
Ainsi, $R_{_{3}}.I_{_{3}}=R_{_{eB}}.I$
Par suite, $I_{_{3}}=\dfrac{R_{_{eB}}.I}{R_{_{3}}}$
A.N : $I_{_{3}}=\dfrac{2\times 1}{3}=\dfrac{2}{3}=0.667$
D'où, $$\boxed{I_{_{3}}=0.667\;A}$$
D'après la loi des nœuds, on a :
$$I=I_{_{3}}+I_{_{4}}$$
Ce qui donne : $I_{_{4}}=I-I_{_{3}}$
A.N : $I_{_{4}}=1-0.667=0.333$
Donc, $$\boxed{I_{_{4}}=0.333\;A}$$
Exercice 8


Commentaires
Younes (non vérifié)
sam, 04/04/2020 - 00:50
Permalien
Solution
Diallo (non vérifié)
mer, 10/21/2020 - 13:24
Permalien
Être le premier de mon lycée
Kat (non vérifié)
ven, 05/27/2022 - 21:05
Permalien
C'était bien
Kat (non vérifié)
ven, 05/27/2022 - 21:05
Permalien
C'était bien
Assane Ngom (non vérifié)
lun, 07/01/2024 - 22:16
Permalien
Vraiment très important ça m
Ajouter un commentaire