Vous êtes ici

Solution des exercices : Généralités sur les forces - 2nd S

Classe:

Seconde

Exercice 1 Mots croisés sur les forces

Exercice 2

1) Lisons les résultats donnés par les dynamomètres dans les cas suivant.

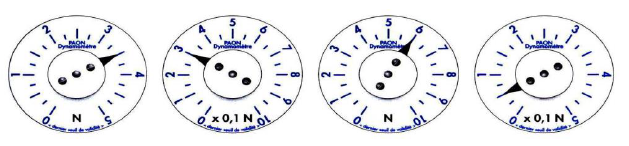
Les dynamomètres indiquent respectivement $3.5\;N\;;\ 0.3\;N\;;\ 6\;N\ $ et $\ 0.05\;N$

2) Une force dont l'intensité est égale à $125\;N$ est représentée par un vecteur qui mesure $5\;cm.$

Déterminons es mesures des longueurs des vecteurs qui représenteraient des forces de $25\;N\;,\ 300\;N\;,\ 480\;N$

On a :

$\dfrac{\ell}{F}=\dfrac{5\;cm}{125\;N}\ \Rightarrow\ \ell=\dfrac{5\;cm}{125\;N}\times F$

Ainsi,

pour $F=25\;N$ on a : $\ell=\dfrac{5\;cm}{125\;N}\times 25\;N=1\;cm$

pour $F=300\;N$ on a : $\ell=\dfrac{5\;cm}{125\;N}\times 300\;N=12\;cm$

pour $F=480\;N$ on a : $\ell=\dfrac{5\;cm}{125\;N}\times 480\;N=19.2\;cm$

3) On a représenté des forces par des vecteurs.

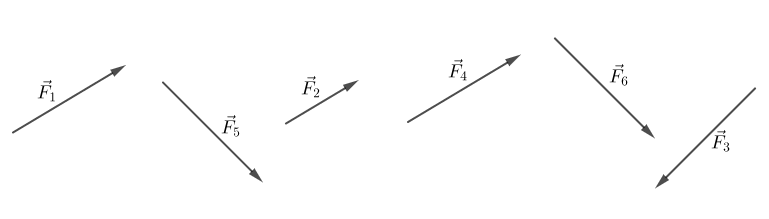
Classons celles qui ont une ou plusieurs caractéristiques communes : direction, sens,....

$$\begin{array}{|l|l|}\hline&\text{Forces}\\\hline\text{Même direction}&\vec{F}_{1}\;,\ \vec{F}_{2}\;,\ \vec{F}_{4}\;,\ \vec{F}_{3}\\\hline\text{Même sens}&\vec{F}_{1}\;,\ \vec{F}_{2}\ \text{ et }\ \vec{F}_{4}\;,\qquad\vec{F}_{6}\ \text{ et }\ \vec{F}_{5}\\\hline\text{Même intensité}&\vec{F}_{3}\;,\ \vec{F}_{5}\ \text{ et }\ \vec{F}_{6}\;,\qquad\vec{F}_{1}\ \text{ et }\ \vec{F}_{4}\\\hline\end{array}$$

Exercice 3

1) Anna est sur une luge tirée par Arthur avec une force $\vec{F}_{1}$ et poussée par Alain avec une force $\vec{F}_{2}.$

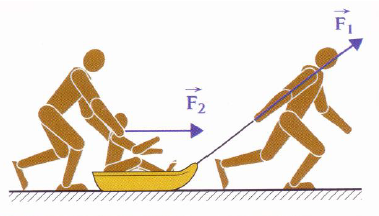
Sachant que l'échelle utilisée est de $1\;cm$ pour $50\;N$, caractérisons $\vec{F}_{1}\ $ et $\ \vec{F}_{2}.$

$$\begin{array}{|l|l|l|l|c|}\hline\text{Force}&\text{Point}&\text{Direction}&\text{Sens}&\text{Valeur (N)}\\&\text{d'application}&&&\\\hline&\text{Point de}&\text{Portée vers}&\text{vers le}&\\\vec{F}_{1}&\text{contact}&\text{la corde}&\text{haut}&120\;N\\&\text{doigts et fil}&&&\\ \hline\vec{F}_{2}&\text{Anna}&\text{horizontal}&\text{vers la}&205\;N\\&&&\text{droite}&\\ \hline\end{array}$$

2. On s'intéresse à la force $\vec{F}$ exercée par l'athlète sur l'anneau.

2.1. Donnons la nature de l'action.

L'action est une action répartie

2.2. Caractérisons et représentons la force $\vec{F}$ de valeur $450\;N.$

$$\begin{array}{|l|l|l|l|c|}\hline\text{Force}&\text{Point}&\text{Direction}&\text{Sens}&\text{Valeur (N)}\\&\text{d'application}&&&\\\hline\vec{F}&\text{contact doigts}&\text{verticale}&\text{dirigé vers}&450\;N\\&\text{et anneau}&&\text{le bas}&\\ \hline\end{array}$$

Représentation

Échelle : $1\;cm$ pour $150\;N$

3. Traçons en rouge et nommons les zones de contact

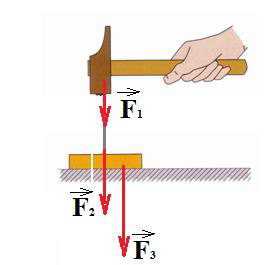
3.1. La force $\vec{F}_{1}$ qui exerce le marteau sur le clou est répartie sur la surface contact entre le marteau et le clou

3.2. La force $\vec{F}_{2}$ qui exerce le clou sur la planche est localisée au point de contact entre le clou et la planche

3.3. La force $\vec{F}_{3}$ qui exerce la planche sur l'établi est répartie sur la surface de contact entre la planche et l'établi

Exercice 4

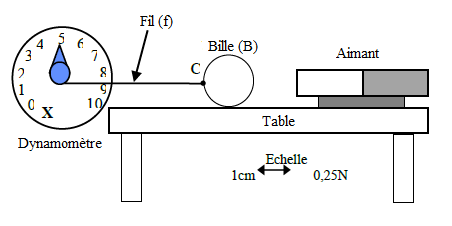
On considère le dispositif de la figure ci-dessous

La masse de la bille est $m=75\;g$

1) Identifions les forces que subit la bille.

Les forces que subit la bille sont :

$-\ $ le poids $\vec{P}$ de la bille

$-\ $ la tension $\vec{T}$ du fil

$-\ $ la force $\vec{F}$ magnétique

2) Précisons pour chaque force son auteur.

$$\begin{array}{|l|l|}\hline\text{Force}&\text{Auteur de la force}\\\hline\text{le poids }\vec{P}\text{ de la bille}&\text{la terre}\\\hline\text{la tension }\vec{T}\text{ du fil}&\text{le fil}\\\hline\text{la force }\vec{F}\text{ magnétique}&\text{l'aimant}\\ \hline\end{array}$$

3) Donnons les caractéristiques de chaque force.

$$\begin{array}{|c|c|c|c|c|}\hline\text{Force}&\text{Point}&\text{Direction}&\text{Sens}&\text{Intensité}\\&\text{d'application}&&&\\\hline\text{le poids }\vec{P}&\text{centre de}&\text{la verticale}&\text{dirigé vers}&0.75\;N\\\text{de la bille}&\text{gravité}&&\text{le bas}&\\\hline\text{la tension }\vec{T}&\text{point}&\text{portée par}&\text{dirigé vers}&0.5\;N\\\text{du fil}&\text{d'attache}&\text{le fil}&\text{le fil}&\\\hline\text{la force }\vec{F}&\text{sur la bille}&\text{horizontale}&\text{dirigé vers}&0.5\;N\\\text{magnétique}&&&\text{l'aimant}&\\\hline\end{array}$$

4) Disons à chaque fois s'il s'agit d'une force de contacte ou à distance, d'une force localisée ou répartie.

$$\begin{array}{|c|c|c|c|c|}\hline\text{Force}&\text{Contact}&\text{Distance}&\text{Localisée}&\text{Répartie}\\\hline\text{le poids }\vec{P}&&\text{à distance}&&\text{répartie}\\\text{de la bille}&&&&\\\hline\text{la tension }\vec{T}&\text{de contact}&&\text{localisée}&\\\text{du fil}&&&&\\\hline\text{la force }\vec{F}&&\text{à distance}&&\text{répartie}\\\text{magnétique}&&&&\\\hline\end{array}$$

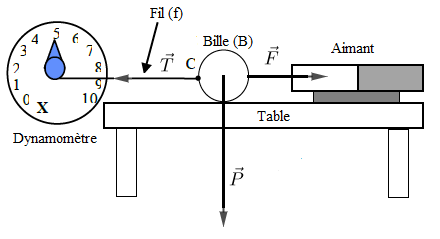
5) Représentation à l'échelle de toutes les forces.

$$\text{Échelle :}\ 1\;cm\ \longrightarrow\ 0.25\;N$$

Exercice 5

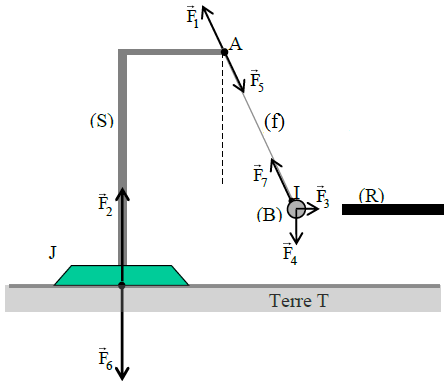
On considère le système de la figure ci-dessous, formé par un support $(S)$, un fil $(f)$, une boule $(B)$ et une règle en plastique dont on a frotté la partie présentée à la boule.

Sur cet ensemble on a représenté quelques forces.

les points $I\;,\ J\ $ et $\ A$ sont des points d'attaches ou de contacts.

1) Complétons le tableau ci-dessous.

$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\vec{F}_{n}&\text{Auteur}&\text{Receveur}&\vec{F}_{.../...}&\text{Nature}&\text{Origine}&\text{Direction}&\text{Sens}&\text{valeur}\\ \hline\vec{F}_{1}&S&f&\vec{T}_{S/f}&\text{de contact}&A&\text{celle du fil}&\text{vers le haut}&1\;N\\ \hline\vec{F}_{2}&T&S&\vec{T}_{T/S}&\text{de contact}&J&\text{celle du support}&\text{vers le haut}&1\;N\\ \hline\vec{F}_{3}&R&B&\vec{T}_{R/B}&\text{à distance}&I&\text{horizontale}&\text{vers la règle R}&1\;N\\ \hline\vec{F}_{4}&T&B&\vec{T}_{T/B}&\text{à distance}&I&\text{verticale}&\text{vers le bas}&1\;N\\ \hline\vec{F}_{5}&f&S&\vec{T}_{f/S}&\text{de contact}&A&\text{celle du fil}&\text{vers le bas}&1\;N\\ \hline\vec{F}_{6}&S&T&\vec{T}_{S/T}&\text{de contact}&J&\text{celle du support}&\text{vers le bas}&1\;N\\ \hline\vec{F}_{7}&f&B&\vec{T}_{f/B}&\text{de contact}&I&\text{celle du fil}&\text{vers le haut}&1\;N\\ \hline\end{array}$$

2) Les forces qui représentent une interaction sont : $\vec{F}_{2}$ et $\vec{F}_{6}\;,\ \vec{F}_{5}$ et $\vec{F}_{1}$

Écrivons la relation vectorielle entre les forces de cette interaction.

$$\vec{F}_{1}+\vec{F}_{5}=\vec{0}\;,\quad \vec{F}_{2}+\vec{F}_{6}=\vec{0}$$

3) a) La boule exerce une force sur le fil .C'est cette force qui fait tendre le fil

b) Caractéristiques de cette force

Cette force a la même direction, même point d'application,même intensité que $\vec{F}_{7}$, mais de sens contraire

c) Représentation de cette force.(Voir figure)

Exercice 6

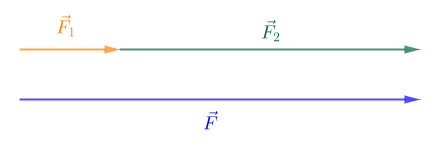
Soient deux forces $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ d'intensité $F_{1}=4\;N\ $ et $\ F_{2}=12\;N$

Représentons et déterminons par calcul l'intensité la résultante $\vec{F}$ des deux forces $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$

On choisira comme échelle : $1\;cm\ \longrightarrow\ 2\;N$

1) $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ ont même direction et même sens

$\begin{array}{rcl}\vec{F}=\vec{F}_{1}+\vec{F}_{2}&\Rightarrow&F=F_{1}+F_{2}\\ \\&\Rightarrow&F=4+12\\ \\&\Rightarrow&F=16\end{array}$

Ainsi, $\boxed{F=16\;N}$

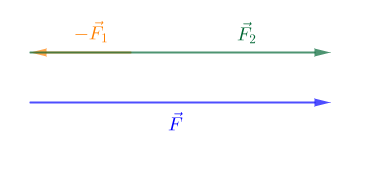
2) $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ ont même direction mais de sens opposés

$\begin{array}{rcl}\vec{F}=\vec{F}_{1}+\vec{F}_{2}&\Rightarrow&F=F_{2}-F_{1}\\ \\&\Rightarrow&F=12-4\\ \\&\Rightarrow&F=8\end{array}$

Donc, $\boxed{F=8\;N}$

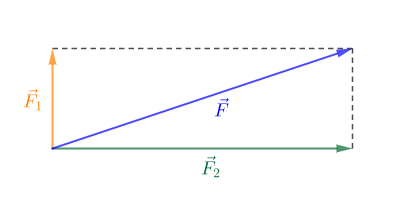
3) $\vec{F}_{1}\ $ et $\ \vec{F}_{2}$ orthogonaux

$\begin{array}{rcl}\vec{F}=\vec{F}_{1}+\vec{F}_{2}&\Rightarrow&F=\sqrt{F_{1}^{2}+F_{2}^{2}}\\ \\&\Rightarrow&F=\sqrt{4^{2}+12^{2}}\\ \\&\Rightarrow&F=\sqrt{16+144}\\ \\&\Rightarrow&F=\sqrt{160}\\ \\&\Rightarrow&F=12.6\end{array}$

D'où, $\boxed{F=12.6\;N}$

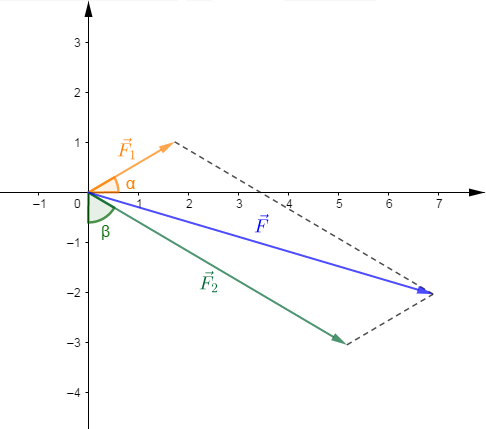
4) $\vec{F}_{1}$ fait un angle $\alpha=30^{\circ}$ avec l'horizontal et dirigé vers haut et $\vec{F}_{2}$ angle $\beta=60^{\circ}$ avec la verticale et dirigé vers le bas

$\begin{array}{rcl}\vec{F}=\vec{F}_{1}+\vec{F}_{2}&\Rightarrow&\vec{F}\left\lbrace\begin{array}{rcl} F_{x}&=&F_{1x}+F_{2x}\\F_{y}&=&F_{1y}+F_{2y}\end{array}\right.\\ \\&\Rightarrow&\vec{F}\left\lbrace\begin{array}{rcl} F_{x}&=&F_{1}\cos\alpha+F_{2}\sin\beta\\F_{y}&=&F_{1}\sin\alpha-F_{2}\cos\beta\end{array}\right.\\ \\&\Rightarrow&F=\sqrt{F_{x}^{2}+F_{y}^{2}}\\ \\&\Rightarrow&F=\sqrt{(F_{1}\cos\alpha+F_{2}\sin\beta)^{2}+(F_{1}\sin\alpha-F_{2}\cos\beta)^{2}}\\ \\&\Rightarrow&F=\sqrt{(4\cos 30^{\circ}+12\sin 60^{\circ})^{2}+(4\sin 30^{\circ}-12\cos 60^{\circ})^{2}}\\ \\&\Rightarrow&F=\sqrt{208}\\ \\&\Rightarrow&F=14.4\end{array}$

Par suite, $\boxed{F=14.4\;N}$

Exercice 7

1) Complétons les phrases à l'aide des mots de la liste : Déformer, modifier, mouvement, mécanique, dynamomètre, mouvement, Newton, objet.

Une action mécanique peut mettre en mouvement un objet Elle peut aussi modifier son mouvement et/ou déformer cet objet.

L'intensité d'une force se mesure en newton à l'aide d'un dynamomètre

2) Rayons dans les phrases ci-dessous les mentions inutiles :

L'action du vent sur un drapeau est une action de contact.

L'action du stylo est une action ponctuelle

L'action de la Terre sur un objet dans son voisinage est une action à distance

L'action d'un aimant sur une bille métallique est une action à distance.

L'action de l'hameçon sur le poisson est une action ponctuelle.

L'action de ma main sur une poignée de porte est une action répartie.

L'action des électrons sur le noyau de l'atome est une action à distance

L'action d'un filin d'amarrage sur le bateau est une action ponctuelle

L'action du pied sur le ballon est une action répartie.

Exercice 8

1. Représentons la force exercée par le marteau sur le clou

$\begin{array}{rcl} \dfrac{1}{F}&=&\dfrac{1\,cm}{50\,N}\\\Rightarrow\;1&=&\dfrac{1,cm}{50\,N}F\ ;\ \\\text{pour}F&=&150\,N\\\Rightarrow\;1&=&\dfrac{1\,cm}{50\,N}\\\Rightarrow\;1&=&3\,cm \end{array}$

fig115

2. Construisons les vecteurs forces $\overrightarrow{F_{1}}$ et $\overrightarrow{F_{2}}$ avec l'échelle $1\,cm\longrightarrow 60N$

$\begin{array}{rcl} 60N\longrightarrow 1\,cm\ ;\ 210N\longrightarrow 3.5\,cm\ ;\ 180N\longrightarrow 3\,cm \end{array}$

Construisons la somme $\overrightarrow{F}$ de ces 2 forces

fig116

Interprétation :

$\blacktriangleright$ Pour avancer de la même façon avec un seul chien l'intensité de la force exercée par ce chien doit-être :

$\begin{array}{rcl} F&=&\dfrac{60N}{1\,cm}\times6.5\,cm\\\Rightarrow\boxed{F=390N} \end{array}$

$\blacktriangleright$Le traîneau n'avance pas tout droit, il dévie du côté du chien $2$

Exercice 9

1. Pour déterminer la résultante de deux forces , on peut utiliser la méthode graphique ou la méthode analytique

fig117

2. Détermination de la somme des deux forces $\overrightarrow{F}$ par méthode analytique

fig118

$\begin{array}{rcl} \overrightarrow{F}&=&\overrightarrow{F_{1}}+\overrightarrow{F_{2}}\\&\Rightarrow&\overrightarrow{F}\begin{array}{lcl} F_{x}&=&F_{x1}+F_{x2}\\ F_{y}&=&F_{y1}+F_{y2} \end{array}\right.\\&\Rightarrow&\overrightarrow{F}\begin{array}{rcl} F_{x}&=&F_{1}\cos\alpha+F_{2}\cos\alpha\\ F_{y}&=&F_{1}\sin\alpha-F_{2}\sin\alpha\\ F_{y}&=&F_{1}\sin\alpha-F_{2}\sin\alpha \end{array}\right.\ ;\\\text{comme}F_{1}&=&F_{2}&\\&\Rightarrow&\overrightarrow{F}\begin{array}{lcl} F_{x}&=&2F_{1}\cos\alpha\\ F_{y}&=&0 \end{array}\right.\\&\Rightarrow\;F&=&2F_{1}\cos\alpha\\&=&2\times100\cos20^{\circ}\\&\Rightarrow&F&=&187.9\,N \end{array}$

Exercice 10

1.1. On mesure la valeur d'une force avec un appareil appelé dynamomètre

1.2. L'unité légale de force est le newton

1.3. Son symbole est $N$

2.1. Les quatre caractéristiques d'une force sont : le point d'application, la direction ,le sens et l'intensité

2.2. Une force est représentée un vecteur

Exercice 11

1. Les actions de contact peuvent être ponctuelles ou réparties.Vrai

2. Faux . L'action du vent sur la voile du véliplanchiste est une action de contact.

3. Faux . L'unité légale de la force est le newton, de symbole $N.$

4. Vrai.La valeur d'une force se mesure avec un dynamomètre.

Exercice 12

Décomposons les forces $P$ et $T$ suivant les directions indiquées.

L'échelle est choisie de sorte que $1\,cm$ correspond à $5N$

fig119

fig120

$\begin{array}{rcl} \overrightarrow{P}&=&\overrightarrow{P_1}+\overrightarrow{P_2}\&\\Rightarrow&\overrightarrow{P}\begin{array}{lcl} P_{1}&=&\dfrac{5N}{1\,cm}\times1.8\,cm\\ P_{2}&=&\dfrac{5N}{1\,cm}\times3\,cm\ \end{array}\right.\\&\Rightarrow&\overrightarrow{P}\begin{array}{lcl} P_{1}&=&9\,N\\ P_{2}&=&15\,N \end{array}\right.\ ;\ \\ \overrightarrow{T}&=&\overrightarrow{T_1}+\overrightarrow{T_2}\\&\Rightarrow&\overrightarrow{T}\begin{array}{rcl} T_{1}&=&\dfrac{5N}{1\,cm}\times2.6\,cm\\ T_{2}&=&\dfrac{5N}{1\,cm}\times2.7\,cm \end{array}\right.\\&\Rightarrow&\begin{array}{lcl} T_{1}&=&13\,N\\ T_{2}&=&13.5\,N \end{array}\right. \end{array}$

Exercice 13

En exerçant des forces F sur trois ressorts différents et en mesurant l'allongement $x$ des ressorts, on a obtenu les représentations

graphiques.

1. Les trois ressorts vérifient la loi de Hooke ,car le graphe représentant la force en fonction de l'allongement

$(F=f(x))$ est une droite linéaire

2. Détermination les constantes de raideur des trois ressorts.

$\begin{array}{rcl} k&=&\dfrac{\Delta F}{\Delta x}\\&\Rightarrow&\;k_{1}=\dfrac{2.3-0}{(5-0)\cdot 10^{-2}}\\&\Rightarrow&\;\boxed{k_{1}=46\,N\cdot\,m^{-1}} \end{array}$

$\begin{array}{rcl} K_{2}=\dfrac{4-0}{(15-0)\cdot10^{-2}}\\\Rightarrow\;\boxed{k_{2}=27\,N\cdot m^{-1}}\ ; \\ \end{array}$

$\begin{array}{rcl}k_{3}=\dfrac{2.5-2}{(20 0)\cdot10^{-2}}\\\Rightarrow\boxed{k_{3}=12.5\,N\cdot m^{-1}} \end{array}$

3. La droite correspond au ressort le plus raide est la droite $(1)$, car possédant la constante de raideur la plus grande

Auteur:

Sidy Mouhamed Ndiaye

Commentaires

Zeyna (non vérifié)

mar, 01/26/2021 - 18:09