Solution des exercices : La cinématique - Ts
Classe:
Terminale
Exercice 1
Un mobile $M_{1}$ est en mouvement relativement au repère d'espace $\mathcal{R}(O\;,\ \vec{i}\;,\ \vec{j})$, son vecteur vitesse est :
$$\overrightarrow{V}_{1}=3\vec{i}+(-2t+4)\vec{j}$$
1) Donnons les lois horaires du mouvement du mobile $M_{1}$ sachant qu'à l'origine des temps, le mobile passe par l'origine $O.$
Cela signifie, par ailleurs, de déterminer les équations horaires du mouvement.
Soit : $\overrightarrow{V}_{1}=3\vec{i}+(-2t+4)\vec{j}$ alors, son vecteur vitesse $\overrightarrow{V}_{1}$ peut s'écrire :
$$\overrightarrow{V}_{1}\left\lbrace\begin{array}{lcl}\dot{x}&=&3\\ \dot{y}&=&-2t+4 \end{array}\right.$$
Or, on sait que : $\overrightarrow{V}_{1}=\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}$ donc, $\overrightarrow{OM}\left\lbrace\begin{array}{lcl}x&=&3t+\text{cte}_{1}\\ y&=&-t^{2}+4t+\text{cte}_{2} \end{array}\right.$
Les constantes seront déterminées en appliquant la condition initiale.
Or, à l'origine des temps, le mobile passe par l'origine $O$ ; ce qui signifie qu'à $t=0$, on a : $x=0\ $ et $\ y=0$
On obtient alors :
$$\left\lbrace\begin{array}{rcl} 3\times0+\text{cte}_{1}&=&0\\-0^{2}+4\times 0+\text{cte}_{2}&=&0\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl}\text{cte}_{1}&=&0\\ \text{cte}_{2}&=&0 \end{array}\right.$$
Par suite, $\overrightarrow{OM}\left\lbrace\begin{array}{lcl}x&=&3t\\ y&=&-t^{2}+4t\end{array}\right.$
D'où, les horaires du mouvement du mobile $M_{1}$ sont données par :
$$\boxed{\overrightarrow{OM}(t)\left\lbrace\begin{array}{lcl}x&=&3t\\ \\y&=&-t^{2}+4t\end{array}\right.}$$
2) Établissons l'équation cartésienne de la trajectoire.
D'après les équations horaires du mouvement du mobile $M_{1}$, on a :
$$\left\lbrace\begin{array}{rcll}x&=&3t&(1)\\ \\y&=&-t^{2}+4t&(2) \end{array}\right.$$
Dans l'équation $(1)$, on exprime $t$ en fonction de $x.$
Ce qui donne : $t=\dfrac{x}{3}$
Ensuite, en remplaçant cette valeur de $t$ dans l'équation $(2)$, on obtient :
$y=-\left(\dfrac{x}{3}\right)^{2}+4\times\dfrac{x}{3}=-\dfrac{x^{2}}{9}+\dfrac{4x}{3}$
D'où, une équation cartésienne de la trajectoire du mobile $M_{1}$ sera donnée par :
$$\boxed{y=-\dfrac{x^{2}}{9}+\dfrac{4x}{3}}$$
3) Expression du vecteur accélération $\vec{a}_{1}.$
Soit :
$\begin{array}{rcl} \vec{a}_{1}&=&\dfrac{\mathrm{d}\overrightarrow{V}_{1}}{\mathrm{d}t}\\ \\&=&\dfrac{\mathrm{d}(3\vec{i}+(-2t+4)\vec{j})}{\mathrm{d}t}\\ \\&=&-2\vec{j} \end{array}$
Ainsi, $\boxed{\vec{a}_{1}=-2\vec{j}}$
Représentation du vecteur accélération $\vec{a}_{1}$ sur la trajectoire de la figure.
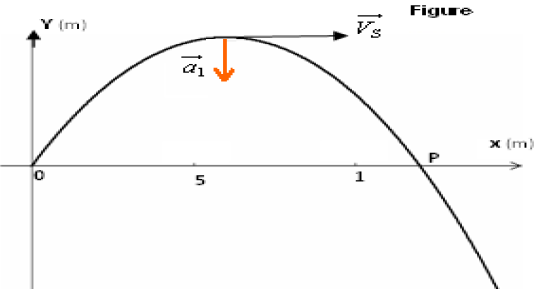
4) Déterminons la date à laquelle la direction du vecteur vitesse est horizontale
Au sommet de la trajectoire, le vecteur vitesse se réduit à sa composante horizontale ; autrement dit, sa composante verticale est nulle.
Ce qui se traduit par : $\dot{y}=-2t+4=0$ soit alors, $t=2\;s$
Ainsi, à $t=2\;s$ la direction du vecteur vitesse est horizontale.
En déduisons les coordonnées $(x_{s}\;;\ y_{s})$ du sommet $S$ de la trajectoire ainsi que la valeur de la vitesse en ce point.
Le mobile atteint le sommet à l'instant $t=2\;s$ donc, en remplaçant cette valeur de $t$ dans les équations horaires du mouvement, on obtient les coordonnées du sommet $S$ de la trajectoire.
Ainsi,
$$S\left\lbrace\begin{array}{rclcl}x_{S}&=&3\times 2&=&6\\ \\y_{S}&=&-(2^{2})+4\times 2&=&4\end{array}\right.$$
D'où, $\boxed{S(6\;;\ 4)}$
Par ailleurs, la valeur de la vitesse sera donnée par :
$$V_{s}=\sqrt{V_{x}^{2}+V_{y}^{2}}$$
Or, au sommet $S$ de la trajectoire le vecteur vitesse est donnée par :
$$\overrightarrow{V}_{1}\left\lbrace\begin{array}{rcl}V_{x}&=&3\\ V_{y}&=&0\end{array}\right.$$
Par suite, $V_{s}=\sqrt{3^{2}+0^{2}}=3\;m\cdot s^{-1}$
D'où, $\boxed{V_{s}=3\;m\cdot s^{-1}}$
Représentation de ce vecteur vitesse (voir figure)
5) Calculons :
$-\ $ Le rayon de courbure de la trajectoire à la date $t=2\;s.$
Soit $\rho=OM$ le rayon de courbure, alors on a :
$\begin{array}{rcl} \rho=OM&=&\sqrt{x^{2}+y^{2}}\\ \\&=&\sqrt{(3\times 2)^{2}+(-(2^{2})+4\times 2)^{2}}\\ \\&=&\sqrt{52}\\ \\&=&7.2\,m \end{array}$
D'où, $\boxed{\rho=7.2\;m}$
$-\ $ L'abscisse $x_{P}$ du mobile lorsque l'ordonnée $y=0.$
D'après les équations horaires, on a :
$$\left\lbrace\begin{array}{rcll}x_{P}&=&3t&(1)\\ \\y_{P}&=&-t^{2}+4t&(2) \end{array}\right.$$
L'ordonnée étant nulle alors, $y_{P}=-t^{2}+4t=0$
Par suite,
$\begin{array}{rcl} -t^{2}+4t=0&\Rightarrow&t(-t+4)=0\\ \\&\Rightarrow&t=0\quad \text{ ou }\quad -t+4=0 \\ \\&\Rightarrow&t=0\;s\quad \text{ ou }\quad t=4\;s\end{array}$
En remplaçant ces valeurs de $t$ dans l'équation $(1)$, on obtient :
Pour $t=0\;s\;,\ x_{P}=3\times 0=0\ \Rightarrow\ x_{P}=0\;m$, le mobile se trouve alors à l' origine du repère.
Pour $t=4\;s\;,\ x_{P}=3\times 4=12\ \Rightarrow\ x_{P}=12\;m$
Donc, l'abscisse $x_{P}$ du mobile lorsque l'ordonnée est nulle sera donnée par :
$$\boxed{x_{P}=12\;m}$$
$-\ $ La valeur de la vitesse $\overrightarrow{V}_{P}$ du mobile au pont $P$
On a :
$\begin{array}{rcl} V_{P}&=&\sqrt{3^{2}+(-2t+4)^{2}}\\\\&=&\sqrt{9+(-2\times 4+4)^{2}}\\\\&=&\sqrt{25}\\ \\&=&5\end{array}$
D'où, $\boxed{V_{P}=5\;m\cdot s^{-1}}$
6) Un deuxième mobile $M_{2}$ en mouvement rectiligne uniformément varié sur l'axe $(Ox)$ du repère $\mathcal{R}(O\;,\ \vec{i}\;,\ \vec{j})$, passe par le point d'abscisse $x=20\;m$ à l'instant $t=0$ avec une vitesse $\overrightarrow{V}_{O_{2}}=2\vec{i}$
Déterminons la valeur algébrique de l'accélération du mobile $M_{2}$ au point du rencontre avec $M_{1}$ pour $x=12\;m$
En considérant les équations horaires, on obtient :
$\ast$ Pour le mobile $M_{1}\ :\ \overrightarrow{OM}_{1}\left\lbrace\begin{array}{lcl}x_{1}&=&3t\\ y_{1}&=&-t^{2}+4t\end{array}\right. $
$\ast$ Pour le mobile $M_{2}\ :\ x_{2}=\dfrac{1}{2}a_{2}t^{2}+V_{0_{2}}t+x_{0_{2}}$
Comme à l'instant $t=0$ le mobile $M_{2}$ passe par le point d'abscisse $x=20\;m$ avec une vitesse $\overrightarrow{V}_{O_{2}}=2\vec{i}$ alors, en remplaçant ces valeurs initiales dans l'équation horaire, on obtient :
$$x_{2}=\dfrac{1}{2}a_{2}t^{2}+2t+20$$
Le mobile $M_{1}$ rencontre le mobile $M_{2}$ lorsque : $x_{1}=x_{2}=12\,m$
Soit $t_{r}$ le temps de rencontre, alors on a :
$x_{1}=3t_{r}=12\ \Rightarrow\ t_{r}=4\;s$
Remplaçons cette valeur de $t_{r}$ dans l'équation horaire du mobile $M_{2}.$
On a :
$\begin{array}{rcl} x_{2}=\dfrac{1}{2}a_{2}t_{r}^{2}+2t_{r}+20&\Rightarrow&12=\dfrac{1}{2}a_{2}(4)^{2}+2\times 4+20\\\\&\Rightarrow&a_{2}=\dfrac{12-28}{8}\\\\&\Rightarrow&a_{2}=-2\end{array}$
Par suite, $\boxed{a_{2}=-2\;m\cdot s^{-2}}$
Exercice 2
1) a) Point de départ du mobile à l'origine des dates
$$\overrightarrow{OM}\left\lbrace\begin{array}{lcl} x&=&t\\ y&=&\dfrac{t^{2}}{2} \end{array}\right.$$
à $t=0s$ $\overrightarrow{OM}\left\lbrace\begin{array}{lcl} x&=&0\\ y&=&\dfrac{0^{2}}{2}=0 \end{array}\right.$
Le mobile se trouve au point $O$ origine du repère
b) Équation de la trajectoire du mobile
$$\overrightarrow{OM}\left\lbrace\begin{array}{lcl} x&=&t\quad(1)\\ y&=&\dfrac{t^{2}}{2}\quad(2) \end{array}\right.$$
$(1)\quad\text{dans }\Rightarrow\;y=\dfrac{1}{2}x^{2}$
c) Détermination des expressions du vecteur vitesse et du vecteur accélération du mobile $M$
$\begin{array}{lcl} \overrightarrow{V}&=&\dfrac{\mathrm{d}\overrightarrow{OM}}{\mathrm{d}t}\\&=&\dfrac{\mathrm{d}\left(t\vec{i}+\dfrac{1} {2}t^{2}\vec{j}\right)}{\mathrm{d}t}\\\Rightarrow\overrightarrow{V}&=&\vec{i}+t\vec{j} \end{array}$
$\begin{array}{lcl} \overrightarrow{a}&=&\dfrac{\mathrm{d}\overrightarrow{V}}{\mathrm{d}t}\\&=&\dfrac{\mathrm{d}\left(\vec{i}+t\vec{j}\right)}{\mathrm{d}t}\\\Rightarrow\overrightarrow{a}&=&t\vec{j} \end{array}$
2) a) Le vecteur vitesse est colinéaire à $\vec{i}$ lorsque sa composante verticale est nulle $V_{y}=0$
A $t=0s$ le vecteur vitesse est colinéaire $\vec{i}$
b) Montrons qu'à la date $t=0s$ la composante tangentielle de l'accélération est nulle
$\begin{array}{lcl} V&=&\sqrt{V_{x}^{2}+V_{y}^{2}}\\&=&\sqrt{1+t^{2}}\\\Rightarrow\;a_{t}&=&\dfrac{\mathrm{d}V}{\mathrm{d}t}\\&=&\dfrac{\mathrm{d}\left(\sqrt{1+t^{2}}\right)}{\mathrm{d}t}\\\Rightarrow\;a_{t}&=&\dfrac{t}{\sqrt{1+t^{2}}}t\\&=&0\\\Rightarrow\;a_{t}&=&\dfrac{0}{\sqrt{1+0^{2}}}\\\Rightarrow\;a_{t}&=&0\,m\cdot s^{-2} \end{array}$
3) a) Montrons que l'accélération normale est $a_{N}=\dfrac{1}{\sqrt{1+t^{2}}}.$
$\begin{array}{lcl} a^{2}&=&a_{n}^{2}+a_{t}^{2}\\\Rightarrow\;a_{n}&=&\sqrt{a^{2}-a_{t}^{2}}\\&=&\sqrt{1^{2}-\left(\dfrac{t}{\sqrt{1+t^{2}}}\right)^{2}}\\&=&\sqrt{\dfrac{1+t^{2}-t^{2}}{1+t^{2}}}\\\Rightarrow\;a_{n}&=&\dfrac{1}{\sqrt{1+t^{2}}} \end{array}$
b) Détermination de la date $t_{1}$ à laquelle $V_{x}=V_{y}$
$V_{x}=V_{y}\Rightarrow\;1=t\Rightarrow\;t_{1}=1s$
c) Calcul du rayon de courbure à la date $t_{1}.$
$\begin{array}{lcl} OM&=&\sqrt{x^{2}+y^{2}}\\&=&\sqrt{t^{2}\left(\dfrac{t^{2}}{2}\right)^{2}}\ t_{1}=1s\\\Rightarrow\;OM&=&\sqrt{1^{2}+\left(\dfrac{1^{2}}{2}\right)^{2}}\\\Rightarrow\;OM&=&1.1\,m \end{array}$
Exercice 3
1) Détermination de la vitesse initiale et de l'abscisse initiale du point mobile $M$
Le mobile $M_{1}$ est animé d'un mouvement rectiligne uniformément varié :
$\begin{array}{lcl} V_{x}&=&a_{1}t+V_{0}\\\Rightarrow\;V_{A}&=&a_{1}t_{1}+V_{0}\\\Rightarrow\;V_{0}&=&V_{A}-a_{1}t_{1}\\&=&6-2\times 1\\\Rightarrow\;V_{0}&=&4\,m\cdot s^{-1} \end{array}$
$\begin{array}{lcl} V_{A}^{2}-V_{0}^{2}&=&2a_{1}\left(x_{A}-x_{0}\right)\\\Rightarrow\;x_{0}&=&x_{A}-\dfrac{V_{A}^{2}-V_{0}^{2}}{2\times 2}\\&=&0-\dfrac{6^{2}-4^{2}}{2\times 2}\\\Rightarrow\;x_{0}&=&-5\,m \end{array}$
2) Loi horaire $x_{1}(t)$ de mouvement de $M_{1}$ et expression de sa vitesse instantanée
$\begin{array}{lcl} x_{1}&=&\dfrac{1}{2}a_{1}t^{2}+V_{0}t+x_{0}\\\Rightarrow\;x_{1}&=&\dfrac{1}{2}\times 2t^{2}+4t-10\\\Rightarrow\;x_{1}&=&t^{2}+4t-5 \end{array}$
$\begin{array}{lcl} V_{1}&=&\dfrac{\mathrm{d}x_{1}}{\mathrm{d}t}\\&=&\dfrac{\mathrm{d}(t^{2}+4t-5)}{\mathrm{d}t}\\\Rightarrow\;V_{1}&=&2t+4 \end{array}$
3) Montrons que le mouvement de $M_{1}$ comporte deux phases
$t\leq t_{1}\ ;\ x_{1}=t^{2}+4t-5$, le mobile $M_{1}$ est animé d'un mouvement rectiligne uniformément varié
$t\geq t_{1}\ ;\ x'_{1}=V_{A}(t-t_{1})+x'_{0}$
$\begin{array}{lcl} \text{A }t&=&t_{1}\;,\ x'_{1}&=&x_{A}\\&=&0\\\Rightarrow\;V_{A}(t-t_{1})+x'_{0}&=&0\\\Rightarrow\;x'_{0}&=&0\\\Rightarrow\;x'_{1}&=&V_{A}(t-t_{1})\\\Rightarrow\;x'_{1}&=&6(t-1) \end{array} \;,\ \text{le mobile }M_{1}\text{ est animé d'un mouvement rectiligne uniforme}$
4) La distance parcourue par le mobile entre la dates $t_{1}=1s$ et $t_{2}=7s$
Exercice 4
1) Représentation de l'allure de la trajectoire
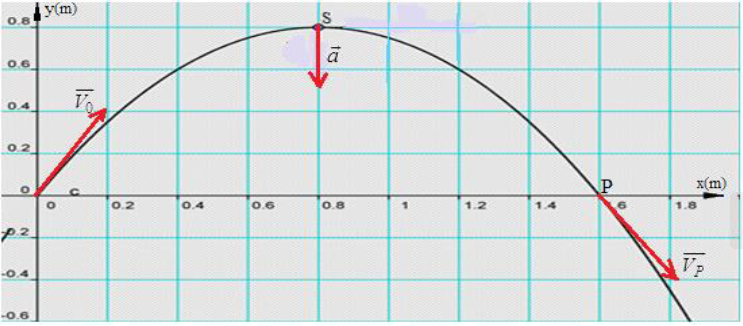
$y=-\dfrac{5}{4}x^{2}+2x$
2) Déterminons l'expression de l'ordonnée $y=f(t)$ du mobile
$\begin{array}{lcl} y&=&-\dfrac{5}{4}x^{2}+2x\text{ or }x=2t\\\Rightarrow\;y&=&-\dfrac{5}{4}(2t)^{2}+2\times 2t\\\Rightarrow\;y&=&-5t^{2}+4t \end{array}$
2) a) Détermination des composantes du vecteur vitesse $\overrightarrow{V}$ en fonction du temps
$$\overrightarrow{V}\left\lbrace\begin{array}{lllll} V_{x}&=&\dfrac{\mathrm{d}x}{\mathrm{d}t}&=&\dfrac{\mathrm{d}(2t)}{\mathrm{d}t}\\ \\ V_{y}&=&\dfrac{\mathrm{d}y}{\mathrm{d}t}&=&\dfrac{\mathrm{d}(-5t^{2}+4t)}{\mathrm{d}t} \end{array}\right.$$
$$\Rightarrow\overrightarrow{V}\left\lbrace\begin{array}{lcl} V_{x}&=&2\\ V_{y}&=&-10t+4 \end{array}\right.$$
b) Date ou direction du vecteur vitesse est horizontale
$V_{y}=-10t+4=0\Rightarrow\;t=\dfrac{4}{10}\Rightarrow\;t=0.4s$
Les coordonnées du sommet $S$ de la trajectoire.
$$S\left\lbrace\begin{array}{lllll} x_{S}&=&2t_{S}&=&2\times 0.4\\ y_{S}&=&-5t_{S}^{2}+4t_{S}&=&-5\times 0.4^{2}+4\times 0.4 \end{array}\right.$$
$$\Rightarrow\;S\left\lbrace\begin{array}{lcl} x_{S}&=&0.8\\ y_{S}&=&0.8 \end{array}\right.$$
Valeur de la vitesse en ce point
$V=V_{x}\Rightarrow\;V=2\,m\cdot s^{-1}$
3) Expression du vecteur accélération $\overrightarrow{a}.$
$\begin{array}{lcl} \overrightarrow{a}&=&\dfrac{\mathrm{d}\overrightarrow{V}}{\mathrm{d}t}\\&=&\dfrac{\mathrm{d}(2\vec{i}+(-10t+4)\vec{j})}{\mathrm{d}t}\\\Rightarrow\overrightarrow{a}&=&-10\vec{j} \end{array}$
Le mouvement du mobile $M$ est uniformément varié
4) Le rayon de courbure de la trajectoire au sommet $S$ de la trajectoire
$\begin{array}{lcl} a&=&\dfrac{v^{2}}{R}\\\Rightarrow\;R&=&\dfrac{v^{2}}{a}\\&=&\dfrac{4}{10}\\&=&0.4\\\Rightarrow\;R&=&0.4\,m \end{array}$
5) Détermination des phases du mouvement
$\overrightarrow{a}\times\overrightarrow{V}>0\Rightarrow\;10(10t-4)>0\Rightarrow\;t>0.4s$ ; le mouvement du mobile $M$ est accéléré
$\overrightarrow{a}\times\overrightarrow{V}<0\Rightarrow\;10(10t-4)<0\Rightarrow\;t<0.4s$ ; le mouvement du mobile $M$ est retardé
6) Détermination de l'abscisse du point $P$ intersection de la trajectoire avec l'axe $Ox$
L'ordonnée du point $P$ est nulle :
$y_{P}=-5t^{2}+4t=0\Rightarrow\;t(-5t+4)=0\Rightarrow\;t=t_{1}=0s$ (le mobile se trouve à l'origine du repère) ou
$\begin{array}{lcl} -5t+4&=&0\\\Rightarrow\;t_{2}&=&\dfrac{4}{5}\\&=&0.8s\\\Rightarrow\;x_{S}&=&2t_{2}\\&=&2\times 0.8s\\\Rightarrow\;x_{S}&=&1.6\,m \end{array}$
Comparons $\overrightarrow{V_{O}}$ et $\overrightarrow{V_{P}}$
$-\ $ Caractéristique du vecteur vitesse $\overrightarrow{V_{O}}$
$\ast\ $ Direction : $\tan\alpha=\dfrac{V_{Oy}}{V_{Ox}}=\dfrac{4}{2}=2\Rightarrow\alpha=63.4^{\circ}$ ; le vecteur vitesse $\overrightarrow{V_{O}}$ fait un angle $\alpha=63.4^{\circ}$ avec l'axe des abscisses.
$\ast\ $ valeur : $V_{0}=\sqrt{V_{Ox}^{2}+V_{Oy}^{2}}=\sqrt{2^{2}+4^{2}}=4.5\,m\cdot s^{-1}$
$-\ $ caractéristique de vecteur vitesse $\overrightarrow{V_{P}}$
$\ast\ $ direction : $\tan\beta=\dfrac{V_{Py}}{V_{Px}}=\dfrac{-10\times 0.8+4}{2}=\dfrac{-4}{2}=-2\Rightarrow\beta=-63.4^{\circ}$ ; le vecteur vitesse $\overrightarrow{V_{P}}$ fait un angle $\beta=-63.4^{\circ}$ avec l'axe des abscisses.
$\ast\ $ valeur : $V_{P}=\sqrt{V_{Px}^{2}+V_{Py}^{2}}=\sqrt{2^{2}+(-10\times 0.8+4)^{2}}=4.5\,m\cdot s^{-1}$
$V_{O}=V_{P}$
Représentation des deux vecteur sur la trajectoire (voir figure)
Exercice 5
1) Calculer de l'accélération $a$ du mouvement
$\begin{array}{lcl} 2a(x_{1}-x_{0})&=&V_{1}^{2}-V_{0}^{2}\\\Rightarrow\;a&=&\dfrac{V_{1}^{2}-V_{0}^{2}}{2(x_{1}-x_{0})}\\&=&\dfrac{4.7^{2}-(-1)^{2}}{2(5-0.5)}\\\Rightarrow\;a&=&2.34\,m\cdot s^{-2} \end{array}$
2) Expression de la vitesse instantanée du mobile
$V(t)=at+x_{0}\Rightarrow\;V(t)=2.34t-1$
3) Instant pour lequel le mobile passe par le point d'abscisse $x_{1}$
$\begin{array}{lcl} V(t_{1})&=&2.34t_{1}-1\\&=&4.7\\\Rightarrow\;t_{1}&=&\dfrac{4.7+1}{2.34}\\\Rightarrow\;t_{1}&=&2.44s \end{array}$
4) Équation horaire du mouvement
$x=\dfrac{1}{2}a(t-t_{0})^{2}+V_{0}(t-t_{0})+cte$
$\begin{array}{lcl} \text{A }t&=&t_{0}\\&=&0s\\\Rightarrow\;x&=&cte\\&=&x_{0}\\&=&0.5\,m\\\Rightarrow\;x&=&\dfrac{1}{2}\times 2.34(t-0)^{2}-1(t-0)+0.5\\\Rightarrow\;x&=&1.17t^{2}-t+0.5 \end{array}$
5) a) Équation horaire du mouvement du mobile $M'$
$x'=v'(t-2)+x'_{0}=4(t-2)+5\\\Rightarrow\;x'=4t-3$
b) Date $t$ de rencontre des mobiles
Les deux mobiles se rencontrent si :
$x=x'\Rightarrow\;1.17t^{2}-t+0.5=4t-3\\\Rightarrow\;1.17t^{2}-5t+3.5=0$
$t_{1}=\dfrac{5-\sqrt{5^{2}-4\times 1.17\times 3.5}}{2\times 1.17}=0.88s$ ; cette solution n'a pas de sens physique (Le second mobile est parti deux secondes après)
$t_{2}=\dfrac{5+\sqrt{5^{2}-4\times 1.17\times 3.5}}{2\times 1.17}=3.39s$ ; solution physique acceptable
c) Abscisse $x$ correspondant à cette rencontre
$x_{r}=4t_{2}-3=4\times 3.39-3\\\Rightarrow\;x_{r}=10.6\,m$
Exercice 6

1) a) Expression, pour la $1^{ière}$ phase, de $x_{C}$ en fonction de $V_{C}$ et $a_{1}$
$\begin{array}{lcl} 2a_{1}(x_{B}-x_{A})&=&V_{C}^{2}-V_{A}^{2}\\\Rightarrow(x_{C}-x_{A})&=&\dfrac{V_{C}^{2}-V_{A}^{2})}{2a_{1}}\\\Rightarrow(x_{C}-0)&=&\dfrac{V_{C}^{2}-0}{2a_{1}}\\\Rightarrow\;x_{C}&=&\dfrac{V_{C}^{2}}{2a_{1}} \end{array}$
b) Expression, pour la $2^{ième}$ phase, de $V_{C}$ en fonction de $a_{2}$, $x_{B}$ et $x_{C}$
$\begin{array}{lcl} 2a_{2}(x_{B}-x_{B})&=&0-V_{C}^{2}\\\Rightarrow(x_{B}-x_{C})&=&-\dfrac{V_{C}^{2}}{2a_{2}}\\\Rightarrow\;x_{C}&=&x_{B}-\dfrac{V_{C}^{2}}{2a_{2}} \end{array}$
c) Expression de $V_{C}$ en fonction de $a_{1}$, $a_{2}$ et $x_{B}$
Calcul de la valeur de $V_{C}$
$\begin{array}{rcl} x_{C}&=&\dfrac{V_{C}^{2}}{2a_{1}}\\ \\&=&x_{B}+\dfrac{V_{C}^{2}}{2a_{2}}\\ \\ \Rightarrow\dfrac{V_{C}^{2}}{2a_{1}}-\dfrac{V_{C}^{2}}{2a_{2}}&=&x_{B}\\ \\\Rightarrow\;V_{C}^{2}\left(\dfrac{1}{2a_{1}}-\dfrac{1} {2a_{2}}\right)&=&x_{B}\\ \\ \Rightarrow\;V_{C}&=&\sqrt{\dfrac{x_{B}}{\left(\dfrac{1}{2a_{1}}-\dfrac{1}{2a_{2}}\right)}} \end{array}$
Calcul de la valeur de $V_{C}$
$\begin{array}{lcl} V_{C}&=&\sqrt{\dfrac{x_{B}}{\left(\dfrac{1}{2a_{1}}-\dfrac{1}{2a_{2}}\right)}}\\ \\&=&\sqrt{\dfrac{300}{\left(\dfrac{1}{2\times 2}-\dfrac{1}{2\times -1}\right)}}\\ \\ \Rightarrow\;V_{C}&=&20\,m\cdot s^{-1} \end{array}$
2) a) Calcul de la distance parcourue $AC$ pendant la $1^{ière}$ phase
$\begin{array}{lcl} x_{C}&=&\dfrac{V_{C}^{2}}{2a_{1}}\\&=&\dfrac{20^{2}}{2\times 2}\\\Rightarrow\;x_{C}&=&100\,m \end{array}$
b) Calcul de la durée du parcours $AC$
$\begin{array}{lcl} V_{C}&=&a_{1}t_{C}\\\Rightarrow\;t_{C}&=&\dfrac{V_{C}}{a_{1}}\\&=&\dfrac{20}{2}\\\Rightarrow\;t_{C}&=&10\,s \end{array}$
3) a) Distance parcourue $CB$ pendant la $3^{ième}$ phase
$CB=AB-BC=300-100\\\Rightarrow\;CB=200\,m$
b) Calcul de la durée du trajet $AB$
$\begin{array}{lcl} V_{B}&=&a_{2}t_{B}+V_{C}\\&=&0\\\Rightarrow\;t_{B}&=&-\dfrac{V_{C}}{a_{2}}\\&=&-\dfrac{20}{-1}\\\Rightarrow\;t_{B}&=&20s \end{array}$
$\begin{array}{lcl} t_{AB}&=&t_{C}+t_{B}\\&=&10+20\\\Rightarrow\;t_{AB}&=&30s \end{array}$
Exercice 7
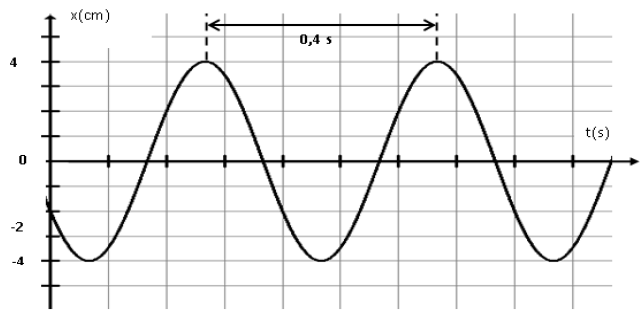
1) a) Détermination de :
$-\ $ la pulsation du mouvement $\omega$
$\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{0.4}=5\pi=15.7\,rad\cdot s^{-1}$
$-\ $ l'élongation initiale $x_{0}$
$x_{0}=-2\,cm$
$-\ $ l'amplitude $x_{m}.$
$x_{m}=4\,cm$
$-\ $ la phase initiale $\varphi.$
$x=x_{m}\cos(\omega\,t+\varphi)$
$\begin{array}{lcl} t&=&0\\\Rightarrow\;x_{m}\cos\varphi&=&x_{0}\\\Rightarrow\cos\varphi&=&\dfrac{x_{0}}{x_{m}}\\&=&\dfrac{-2}{4}\\&=&-\dfrac{1}{2}\\\Rightarrow\left\lbrace\begin{array}{lllll} \varphi&=&\dfrac{\pi}{3}+\pi&=&\dfrac{4\pi}{3}\\ \\ \varphi&=&-\dfrac{\pi}{3}+\pi&=&\dfrac{2\pi}{3} \end{array}\right. \end{array}$
$\begin{array}{lcl} v&=&\dfrac{\mathrm{d}x}{\mathrm{d}t}\\&=&\dfrac{\mathrm{d}(x_{m}\cos(\omega\,t+\varphi))}{\mathrm{d}t}\\&=&-x_{m}\varphi\sin(\omega\,t+\varphi) \end{array}$
$\begin{array}{lcl} \text{A }t=0\;,\ v(0)&=&-x_{m}\omega\sin\varphi\\&=&v_{0}>0\\\Rightarrow\sin\varphi<0\Rightarrow\varphi&=&\dfrac{4\pi}{3} \end{array}$
b) Loi horaire $x=f(t).$
$x=4\cdot 10^{-2}\cos\left(5\pi\,t+\dfrac{4\pi}{3}\right)$
2) a) Détermination de l'expression de la vitesse en fonction du temps.
$\begin{array}{lcl} v&=&\dfrac{\mathrm{d}x}{\mathrm{d}t}\\&=&\dfrac{\mathrm{d}\left(4\cdot 10^{-2}\cos\left(5\pi\,t+\dfrac{4\pi}{3}\right)\right)}{\mathrm{d}t}\\&=&-4\cdot 10^{-2}\times 5\pi\sin\left(5\pi\,t+\dfrac{4\pi}{3}\right)\\\Rightarrow\;v&=&20\cdot 10^{-2}\pi\sin\left(5\pi\,t+\dfrac{4\pi}{3}\right) \end{array}$
b) Valeur algébrique de la vitesse initiale $\overrightarrow{V_{0}}.$
$\begin{array}{lcl} v(0)&=&v_{0}\\&=&-x_{m}\omega\sin\varphi\\&=&-4\cdot 10^{-2}\times 5\pi\sin\dfrac{4\pi}{3}\\\Rightarrow\;v_{0}&=&0.544\,m\cdot s^{-1} \end{array}$
3) a) Détermination graphique de $t_{1}$
$t_{1}=0.4s$
b) Détermination de $t_{1}$ par le calcul.
$\begin{array}{lcl} x&=&-x_{0}\\4\cdot 10^{-2}\cos\left(5\pi\,t+\dfrac{4\pi}{3}\right)&=&-2\cdot 10^{-2}\\\Rightarrow\cos\left(5\pi\,t+\dfrac{4\pi}{3}\right)&=&-\dfrac{1}{2}\\\Rightarrow\cos\left(5\pi\,t+\dfrac{4\pi}{3}\right)&=&\cos\left(\dfrac{4\pi}{3}+2k\pi\right)\\\Rightarrow5\pi\,t+\dfrac{4\pi}{3}&=&\dfrac{4\pi}{3}+2k\pi\\\Rightarrow\;t&=&\dfrac{2k}{5}k=1\\\Rightarrow\;t&=&\dfrac{2}{5}\\&=&0.4s \end{array}$
4) Détermination de la valeur algébrique de la vitesse du solide lors de son premier passage par la position d'abscisse $x=2\,cm$
Exercice 8
1) Nature de mouvement du mobile.
L'accélération angulaire est constante et la trajectoire est un cercle, le mouvement est circulaire uniformément varié.
2) Expressions de sa vitesse angulaire $\dot{\theta}$ et de son élongation angulaire $\theta$ en fonction du temps.
$\ddot{\theta}=\ddot{\theta}(t-t_{0})+cte$
$\begin{array}{lcl} t&=&t_{0}\\&=&0\\\Rightarrow\ddot{\theta}&=&cte\\&=&\dot{\theta_{0}}\\&=&2\pi\,rad\cdot s^{-1}\\\Rightarrow\dot{\theta}&=&-\dfrac{\pi}{5}t+2\pi \end{array}$
$\begin{array}{lcl} \dfrac{\mathrm{d}\theta}{\mathrm{d}t}&=&\dot{\theta}\\&=&-\dfrac{\pi}{5}t+2\pi\\\Rightarrow\theta&=&-\dfrac{1}{2}\dfrac{\pi}{5}t^{2}+2\pi\,t+cte \end{array}$
$\begin{array}{lcl} \theta(0)&=&-\dfrac{1}{2}\dfrac{\pi}{5}\times 0^{2}+2\pi\times 0+cte\\&=&\dfrac{\pi}{3}\\\Rightarrow\,cte&=&\dfrac{\pi}{3}\\\Rightarrow\theta&=&-\dfrac{\pi}{10}t^{2}+2\pi\,t+\dfrac{\pi}{3} \end{array}$
3) a) Montrons que le mouvement du mobile comporte deux phases.
$\begin{array}{lcl} \ddot{\theta}\dot{\theta}&>&0\\\Rightarrow\dfrac{\pi}{5}\left(\dfrac{\pi}{5}t-2\pi\right)&>&0\\\Rightarrow\dfrac{\pi}{5}t-2\pi&>&0\\\Rightarrow\dfrac{t}{5}&>&2\\\Rightarrow\;t&>&10s \end{array}\ ;\ $
le mouvement du mobile est accéléré
$\begin{array}{lcl} \ddot{\theta}\dot{\theta}&<&0\\\Rightarrow\dfrac{\pi}{5}\left(\dfrac{\pi}{5}t-2\pi\right)&<&0\\\Rightarrow\dfrac{\pi}{5}t-2\pi&<&0\\\Rightarrow\dfrac{t}{5}&<&2\\\Rightarrow\;t&<&10s \end{array}\ ;\ $
le mouvement du mobile est retardé
b) Détermination du nombre de tours effectué par le mobile pendant la première phase du mouvement
Première phase : $t=10s$
$\begin{array}{lcl} n&=&\dfrac{\theta}{2\pi}\\&=&\dfrac{-\dfrac{\pi}{10}t^{2}+2\pi\,t+\dfrac{\pi}{3}}{2\pi}\\&=&\dfrac{-\dfrac{\pi}{10}10^{2}+2\pi\times 10+\dfrac{\pi}{3}}{2\pi}\\\Rightarrow\;n&=&5\;tours \end{array}$
4) Calcul à la date $t_{1}$
a) De la vitesse angulaire $\dot{\theta_{1}}$ et de la vitesse linéaire du mobile.
$\begin{array}{lcl} \dot{\theta}&=&-\dfrac{\pi}{5}t+2\pi\\\Rightarrow\dot{\theta_{1}}&=&-\dfrac{\pi}{5}t_{1}+2\pi\\&=&-\dfrac{\pi}{5}\times 20+2\pi\\\Rightarrow\dot{\theta}&=&-2\pi\;rad\cdot s^{-1} \end{array}$
$V=R\left|\dot{\theta_{1}}\right|=25\cdot 10^{-2}\times 2\pi\\\Rightarrow\;V=1.57\,m\cdot s^{-1}$
b) de l'accélération normale et de l'accélération tangentielle du mobile.
$\begin{array}{lcl} a_{n}&=&R\dot{\theta^{2}}\\&=&25\cdot 10^{-2}\times(-2\pi)^{2}\\\Rightarrow\;a_{n}&=&9.87\,m\cdot s^{-2} \end{array}$
$\begin{array}{lcl} a_{t}&=&R\ddot{\theta}\\&=&25\cdot 10^{-2}\times-\dfrac{\pi}{5}\\\Rightarrow\;a_{t}&=&-0.157\,m\cdot s^{-2} \end{array}$
Valeur de son accélération linéaire.
$\begin{array}{lcl} a&=&\sqrt{a_{n}^{2}+a_{t}^{2}}\\&=&\sqrt{9.87^{2}+(-0.157)^{2}}\\\Rightarrow\;a&=&9.87\,m\cdot s^{-2} \end{array}$
5) a) Période et fréquence du mouvement
$T=\dfrac{2\pi}{\left|\dot{\theta_{1}}\right|}=\dfrac{2\pi}{\left|-2\pi\right|}\\\Rightarrow\;T=1s$
$N=\dfrac{1}{T}\Rightarrow\;N=1\,Hz$
b) Montrons que l'accélération linéaire d'un mouvement circulaire uniforme est égale à l'accélération normale.
$\overrightarrow{a}=\overrightarrow{a_{t}}+\overrightarrow{a_{n}}$
$\begin{array}{lcl} \dot{\theta}&=&cte\\\Rightarrow\ddot{\theta}&=&0\\\Rightarrow\overrightarrow{a_{t}}&=&R\ddot{\theta}\overrightarrow{u_{n}}\\&=&\overrightarrow{0}\\\Rightarrow\overrightarrow{a}&=&\overrightarrow{a_{n}} \end{array}$
Exercice 9

1) a) Détermination de l'accélération $a_{1}$
$\begin{array}{lcl} 2a_{1}(x_{1}-x_{0})&=&v_{1}^{2}-v_{0}^{2}\\\Rightarrow\;a_{1}&=&\dfrac{v_{1}^{2}-v_{0}^{2}}{2(x_{1}-x_{0})}\\&=&\dfrac{21^{2}-16^{2}}{2\times 100}\\\Rightarrow\;a_{1}&=&0.925\,m\cdot s^{-2} \end{array}$
b) Détermination la date $t_{1}$
$v=a_{1}(t-t_{0})+v_{0}$
A $t=t_{0}=0$,
$\begin{array}{lcl} v_{0}&=&16\,m\cdot s^{-1}\\\Rightarrow\;v&=&a_{1}t+v_{0}\\\Rightarrow\;v_{1}-v_{0}&=&a_{1}t_{1}\\\Rightarrow\;t_{1}&=&\dfrac{v_{1}-v_{0}}{a_{1}}\\&=&\dfrac{21-16}{0.925}\\\Rightarrow\;t_{1}&=&5.41s \end{array}$
c) Loi horaire du mouvement de la voiture pour $t\in\left[0\;,\ t_{1}\right]$
De manière générale, $x=\dfrac{1}{2}a_{1}(t-t_{0})^{2}+v_{0}(t-t_{0})+x_{0}$ ;
comme : $t_{0}=0\;,\ v_{0}=16\,m\cdot s^{-1}\text{ et }x_{0}=0$
$\Rightarrow\;x=\dfrac{1}{2}a_{1}t^{2}+v_{0}t$
$\Rightarrow\dfrac{1}{2}\times 0.925\,t^{2}+16t=0.463\,t^{2}+16t$
2) a) Loi horaire du mouvement de la voiture pour $t\geq t_{1}$
$x=v_{1}(t-t_{1})+x_{1}=21(t-5.41)+100$
$\Rightarrow\;x=21t-13.6$
b) Vérifions si la voiture passe ou non devant le feu lorsqu'il est vert
Temps mis pour parcourir les $100\,m$ qui restent à parcourir
$x_{1}=21t-13.6$
$\begin{array}{lcl} x&=&21t_{2}-13.6\\&=&100\\\Rightarrow\;t_{2}&=&\dfrac{100+13.6}{21}\\\Rightarrow\;t_{2}&=&5.41s \end{array}$
Temps mis pour parcourir les $200\,m$
$t_{1}+t_{2}=5.41s+5.41s=10.82s\neq 11s$ la voiture passera devant le feu vert.
3) a) Calcul de la distance parcourue par la voiture du début de freinage jusqu'à son arrêt
$\begin{array}{lcl} 0^{2}-v_{1}^{2}&=&2a_{2}d\\\Rightarrow\;d&=&-\dfrac{v_{1}^{2}}{2a_{2}}\\&=&-\dfrac{21^{2}}{2\times -2}\\\Rightarrow\;d&=&110.25\,m\cdot s^{-1} \end{array}$
b) Détermination de la vitesse $v_{2}$ de la voiture en passant devant le feu
$\begin{array}{lcl} v_{2}^{2}-v_{1}^{2}&=&2a_{2}d\\\Rightarrow\;v_{2}^{2}&=&2a_{2}d+v_{1}^{2}\\\Rightarrow\;v_{2}&=&\sqrt{2a_{2}d+v_{1}^{2}}\\&=&\sqrt{2\times -2\times 100+21^{2}}\\\Rightarrow\;v_{2}6.40\,m\cdot s^{-1} \end{array}$
La date $t_{2}$ correspondante au passage de la voiture
$\begin{array}{lcl} v_{2}-v_{1}&=&a_{2}(t_{2}-t_{1})\\\Rightarrow\;t_{2}&=&\dfrac{v_{2}-v_{1}}{a_{2}}+t_{1}\\&=&\dfrac{6.40-21}{-2}+5.41\\\Rightarrow\;t_{2}&=&12.71s \end{array}$
c) $t_{2}=12.71s>11s$ la voiture est passée lorsque le feu n'est plus vert.

Commentaires
Anonyme (non vérifié)
sam, 01/02/2021 - 06:31
Permalien
Où est le pdf
Anonyme (non vérifié)
ven, 01/22/2021 - 01:46
Permalien
Ou est le pdf
Ibrahima ba (non vérifié)
ven, 02/05/2021 - 23:28
Permalien
Je vous remercie pour ces
Mareme (non vérifié)
lun, 11/29/2021 - 21:48
Permalien
Question
Baptiste (non vérifié)
mar, 02/15/2022 - 18:02
Permalien
Erreur
bara ndiaye (non vérifié)
ven, 08/26/2022 - 20:11
Permalien
reponse à erreur
Anonyme (non vérifié)
lun, 08/22/2022 - 02:59
Permalien
Nice
Chamsou (non vérifié)
dim, 11/06/2022 - 06:40
Permalien
Je veux ce documents
Chamsou (non vérifié)
dim, 11/06/2022 - 06:41
Permalien
Je veux ce documents
Mayssoune (non vérifié)
jeu, 09/28/2023 - 14:33
Permalien
Je veux ce document
Anonyme (non vérifié)
jeu, 09/28/2023 - 14:36
Permalien
Je veux ce document
GORA GUEYE (non vérifié)
sam, 11/18/2023 - 21:22
Permalien
Ça doit être plus développé
Hamidoune (non vérifié)
lun, 11/18/2024 - 23:17
Permalien
Etude
Ajouter un commentaire