Solution des exercices : Le courant électrique 3e
Classe:
Troisième
Exercice 1
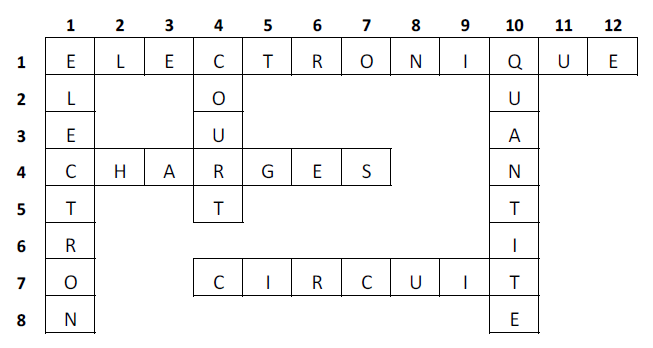
Exercice 2
1) Trouvons la quantité d'électricité ainsi transportée.
On a : $I=\dfrac{q}{t}\ \Rightarrow\ q=I\times t\ $ avec, $t=2\;h=2\times 60\times 60=7\,200\;s$
A.N : $q=1\;10^{-3}\times 7\,200=7.2$
Donc $$\boxed{q=7.2\;C}$$
2) Calculons le nombre d'électrons correspondant.
On a : $q=n.e\ \Rightarrow\ n=\dfrac{q}{e}$
A.N : $n=\dfrac{7.2}{1.6\;10^{-19}}=4.5\;10^{19}$
Donc $$\boxed{n=4.5\;10^{19}}$$
Exercice 3
1) Calculons en ampère-heure $(Ah)$, la quantité d'électricité en mouvement.
On a : $q=I\times t\ $ avec, $\ I=3\;mA=3\;10^{-3}\;A\ $ et $\ t=1\;h$
A.N : $q=3\;10^{-3}\times 1=3\;10^{-3}$
Donc $$\boxed{q=3\;10^{-3}\;Ah}$$
2) Calculons le nombres de charges électriques en circulation pendant une minute.
On a : $q(Amn)=\dfrac{q(Ah)}{60}$
A.N : $q(Amn)=\dfrac{3\;10^{-3}}{60}=5\;10^{-5}\;Amn$
Or, $q=n.e\ \Rightarrow\ n=\dfrac{q}{e}$
A.N : $n=\dfrac{5\;10^{-5}}{1.6\;10^{-19}}=3.125\;10^{14}$
Donc $$\boxed{n=3.125\;10^{14}}$$
Leur nature : ce sont des électrons.
Exercice 4
1) Trouvons le nombre d'électrons qui traversent ce circuit pendant ce temps.
On a : $q=n.e\ \Rightarrow\ n=\dfrac{q}{e}$
A.N : $n=\dfrac{30}{1.6\;10^{-19}}=1.875\;10^{20}$
Donc $$\boxed{n=1.875\;10^{20}}$$
2) L'intensité du courant électrique dans ce circuit est donnée par
$I=\dfrac{q}{t}$
A.N : $I=\dfrac{30}{60}=0.5$
Donc $$\boxed{I=0.5\;A}$$
Exercice 5
1) Donnons la nature du courant électrique dans chacun des cas suivants :
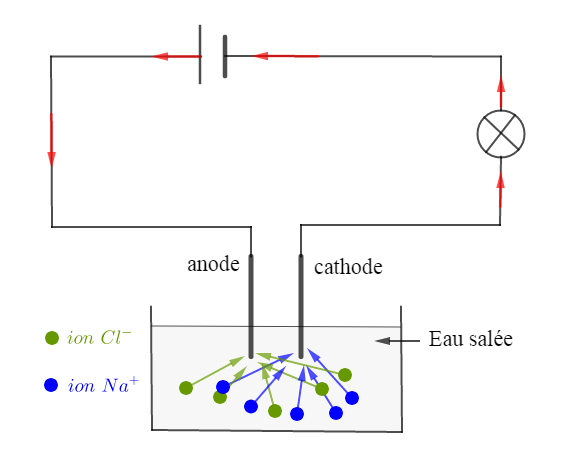
$-\ $ Dans un conducteur métallique, le courant est produit par un déplacement d'électrons.
$-\ $ Dans un électrolyte, le courant est dû à un déplacement d'ions.
2) Reproduisons le schéma et représentons le sens du courant électrique par des flèches rouges entre les dipôles et dans l'électrolyseur ; indiquons sur chaque ion par une flèche en bleu le sens de déplacement des porteurs de charge positive et en vert le sens de déplacement des porteurs de charge négative.

Exercice 6
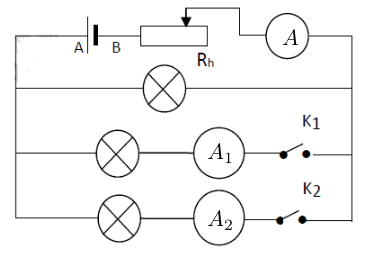
Dans le circuit ci-dessous, toutes les lampes sont identiques.

Le rhéostat permet de maintenir constante l'intensité délivrée par le générateur $I=300\;mA$ pour chaque expérience.
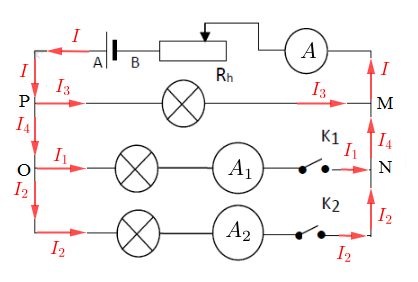
1) Indiquons le sens du courant dans chaque branche

2) Dans ce circuit, il y a quatre nœuds : $M\;;\ N\;;\ O\;;\ P$
Énonçons la loi des nœuds : l'intensité des courants qui arrivent à un nœud est toujours égale à celle des courants qui en partent.
3) Pour chacun des cas suivants, indiquons les valeurs affichées par les ampèremètres $A\;,\ A_{1}\ $ et $\ A_{2}.$
Premier cas : on ferme l'interrupteur $K_{1}$ seul. Alors, la branche $NK_{2}O$ ne marche plus. Donc, $I_{2}=0$
Par suite, l'ampèremètre $A_{2}$ affiche $0\;mA$
$I=300\;mA$ donc, l'ampèremètre $A$ affiche $300\;mA$
$-\ $ Au niveau du nœud $P$, on a : $I=I_{3}+I_{4}$
$-\ $ Au niveau du nœud $O$, on a : $I_{4}=I_{1}+I_{2}$
Or, $I_{2}=0\ $ donc, $I_{4}=I_{1}$
De plus les lampes sont toutes identiques.
Ainsi, $I_{3}=I_{1}$ et par suite, $I_{1}=\dfrac{I}{2}=\dfrac{300}{2}=150$
Donc, $I_{1}=150\;mA$
D'où, l'ampèremètre $A_{1}$ affiche $150\;mA$
Deuxième cas : on ferme $K_{2}$ seul.
On procède comme dans le premier cas, on obtient alors :
$A_{1}$ affiche $0\;mA$
$A$ affiche $300\;mA$
$A_{2}$ affiche $150\;mA$
Troisième cas : on ferme $K_{1}$ et $K_{2}.$
Toutes les lampes étant identiques donc, on obtient la même intensité au niveau de chaque lampe.
Cette intensité est donc égale à $\dfrac{I}{3}=\dfrac{300}{3}=100\;mA$
Ainsi, les ampèremètre $A_{1}\ $ et $\ A_{2}$ affichent $100\;mA$
l'ampèremètre $A$ étant traversé par $I=300\;mA$ donc, il affiche $300\;mA$
Exercice 7
Une quantité d'électricité $Q=1800\;C$ traverse un circuit pendant une durée $t=3\;\text{minutes}.$
1) Trouvons la valeur de l'intensité $I$
On sait que la quantité d'électricité $Q$ qui traverse un circuit pendant une durée $t$ est donnée par :
$$Q=I\times t$$
Ce qui donne : $I=\dfrac{Q}{t}$
Comme le temps $t$ est exprimé en minutes alors, on va d'abord le convertir en secondes :
On a : $1\;mn\rightarrow 60\;s$ donc, $3\;mn\rightarrow 3\times 60\;s=180\;s$
Par suite : $I=\dfrac{1800}{180}=10$
D'où, $$\boxed{I=10\;A}$$
2) Trouvons le nombre d'électrons qui traversent le circuit par seconde
On a : $Q=I\times t$
De plus, $Q$ peut encore s'exprimer par : $Q=n\times e$
Donc, on obtient l'égalité suivante :
$$n\times e=I\times t$$
Par suite, $n=\dfrac{I\times t}{e}\ $ avec, $I=10\;A\ $ et $\ t=1\;s$
A.N : $n=\dfrac{10}{1.6\;10^{-19}}=6.25\,10^{19}$
Ainsi, $6.25\,10^{19}$ électrons traversent le circuit chaque seconde.
Exercice 8
Un fil électrique est parcouru par un courant d'intensité $I=3\;mA.$
1) Trouvons la quantité d'électricité traversant le circuit pendant une minute
On sait que la quantité d'électricité traversant un fil électrique est parcouru par un courant d'intensité $I$ pendant une durée $t$ est donnée par :
$$Q=I\times t$$
Or, $t=1\;mn=60\;s\ $ et $\ I=3\;mA=3\cdot 10^{-3}\;A$
A.N : $Q=3\cdot 10^{-3}\times 60=0.18$
D'où, $$\boxed{Q=0.18\;C}$$
2) Trouvons le nombres de charges électriques en circulation pendant une minute et précisons leur nature
La quantité d'électricité $Q$ traversant ce fil électrique peut encore s'exprimer par :
$$Q=n\times e$$
Ce qui donne alors : $n=\dfrac{Q}{e}$
A.N : $n=\dfrac{0.18}{1.6\cdot10^{-19}}$
D'où, $1.125\cdot 10^{18}$ charges électriques sont en circulation dans le fil pendant durée égale à une minute.
Ces charges électriques sont des électrons.
Exercice 9
Le nombre d'électrons qui traverse la section d'un circuit est $2\cdot 10^{18}$ pour une intensité de $2.5\;mA$
1) Trouvons la quantité d'électricité qui traverse ce circuit.
Soit : $Q=n\times e$
A.N : $Q=2\cdot 10^{18}\times 1.6\;10^{-19}$
D'où, $$\boxed{Q=0.32\;C}$$
2) Déterminons alors la durée de passage du courant électrique dans ce circuit.
On sait que la quantité d'électricité qui traverse un circuit parcouru par un courant d'intensité $I$ peut encore s'écrire :
$$Q=I\times t$$
Ainsi, $t=\dfrac{Q}{I}$
A.N : $t=\dfrac{0.32}{2.5\;10^{-3}}=128$
Donc, $$\boxed{t=128\;s}$$
Exercice 10
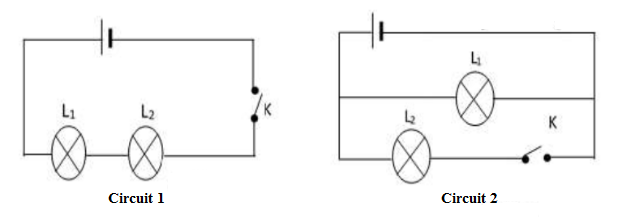
On considère les deux circuits ci-dessous.

1) Le circuit étant à chaque fois fermé, expliquons ce qui se passe si le filament d'une lampe se détériore :
$-\ $ Pour le circuit 1 : le montage est en série. Alors, si un filament se détériore toutes les lampes s'éteignent car, le circuit est ouvert et le courant ne circule plus.
$-\ $ Pour le circuit 2 : le montage est en parallèle. Donc, les lampes ne sont pas traversées par le même courant. Ainsi, si le filament de l'une des lampes se détériore alors, cette lampe s'éteint. Par contre, l'autre lampe s'allume puisque sa branche reste fermée.
2) Pour installer deux ampoules dans un couloir, le meilleur montage est celui en dérivation : circuit 2
Parce que, avec ce montage, si l'une des lampes se détériore, l'autre peut encore continuer à fonctionner. D'où, l'avantage de ce montage.
Par contre, pour le montage 2, la détérioration de l'une des lampes entraine systématiquement le non fonctionnement de l'autre.
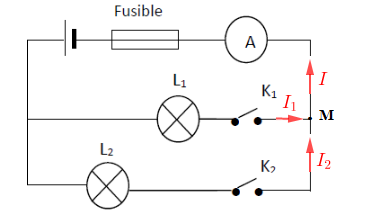
Exercice 11
Le circuit ci-dessous comprend un fusible de $500\;mA$, une pile de $4.5\;V$, une première lampe $L_{1}$ portant les indications $4.5\;V\;-\;0.15\;A$ et une deuxième lampe $L_{2}$ dont les indications sont : $4.5\;V\;-\;350\;mA.$

1) Les indications sur les lampes signifient la tension et l'intensité du courant appropriés à chaque lampe pour son bon fonctionnement.
2) Si on ferme $K_{1}$ seul, l'ampèremètre affichera $0.15\;A$ car, c'est la seule valeur de l'intensité suffisante à la lampe pour qu'elle s'allume.
En effet, d'après la loi des nœuds, le courant $I$ mesuré par l'ampèremètre est donné par :
$$I=I_{1}+I_{2}$$
$K_{2}$ étant ouvert donc, aucun courant ne passe par $L_{2}.$
D'où, $I_{2}=0$ et par suite, $I=I_{1}$
Par conséquent, l'ampèremètre $(A)$ affichera $I_{1}=0.15\;A$
3) Si les deux interrupteurs $K_{1}\ $ et $\ K_{2}$ sont fermés, alors l'ampèremètre indiquera $500\;mA$ car, c'est la somme des deux intensités parcourant les deux lampes.
En effet, au niveau le nœud $M$, en appliquant la loi des nœuds, on obtient :
$\begin{array}{rcl} I&=&I_{1}+I_{2}\\&=&0.15\;A+350\;mA\\&=&150\;mA+350\;mA\\&=&500\;mA\end{array}$
Donc, $I=500\;mA$
Comme l'ampèremètre $(A)$ mesure l'intensité $I$ alors, il affichera $500\;mA$
4) Les deux interrupteurs $K_{1}\ $ et $\ K_{2}$ restant fermés, en remplaçant $L_{1}$ par une lampe portant les indications : $4.5\;V\;-\;0.25\;A$ et en appliquant la loi des nœuds, on obtient une intensité $I$ donnée par :
$\begin{array}{rcl} I&=&I_{1}+I_{2}\\&=&0.25\;A+350\;mA\\&=&250\;mA+350\;mA\\&=&600\;mA\end{array}$
Ainsi, le courant mesuré par l'ampèremètre est d'intensité $I=600\;mA$
On remarque que cette valeur est supérieure à l'intensité maximale $(500\;mA)$ pouvant traverser la fusible.
Par conséquent, la fusible va se griller par fusion et le circuit s'ouvre.
5) Le rôle du fusible est d'ouvrir un circuit électrique lorsque l'intensité du courant électrique dans celui-ci atteint une valeur donnée pendant un certain temps.
On l'appelle fusible du fait qu'il y a fusion d'un filament conducteur sous l'effet de son élévation de température provoquée par la surintensité.

Commentaires
Anonyme (non vérifié)
lun, 06/15/2020 - 16:33
Permalien
pdf
Anonyme (non vérifié)
jeu, 08/06/2020 - 03:46
Permalien
Excellent
Anonyme (non vérifié)
ven, 06/18/2021 - 23:51
Permalien
Merci beaucoup
Anonyme (non vérifié)
dim, 07/11/2021 - 11:19
Permalien
EXERCICE 2: la solution est
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:09
Permalien
C'est une très bonne
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:09
Permalien
C'est une très bonne
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:09
Permalien
C'est une très bonne
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:09
Permalien
C'est une très bonne
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:09
Permalien
C'est une très bonne
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:09
Permalien
C'est une très bonne
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:09
Permalien
C'est une très bonne
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:09
Permalien
C'est une très bonne
Fallou ba (non vérifié)
mer, 07/14/2021 - 23:10
Permalien
C'est une très bonne
Nicia (non vérifié)
sam, 10/16/2021 - 21:44
Permalien
Erreur (correction)
Nicia (non vérifié)
sam, 10/16/2021 - 21:46
Permalien
Erreur sur mon 1er comment
NDIAYE e (non vérifié)
mer, 06/15/2022 - 22:29
Permalien
ORDINATEUR
Anonyme (non vérifié)
dim, 07/03/2022 - 23:31
Permalien
La première question de l
Anonyme (non vérifié)
jeu, 03/09/2023 - 09:05
Permalien
Merci infiniment pour cet
Anonyme (non vérifié)
dim, 05/21/2023 - 10:18
Permalien
Mohamed pam un ampereheure
Mourtala Sambe (non vérifié)
jeu, 05/25/2023 - 23:49
Permalien
Merci
Aïssata (non vérifié)
ven, 03/22/2024 - 23:26
Permalien
Merci
Ajouter un commentaire