Solution des exercices : Propagation rectiligne de la lumière - 2nd S
Classe:
Seconde
Exercice 1
Choisissons les objets lumineux qui sont des sources primaires, et ceux qui sont des sources secondaires.
$$\begin{array}{|l|l|}\hline\text{Sources primaires}&\text{Sources secondaires}\\\hline\text{Flamme de bougie}&\text{Ecran de protection}\\\text{Soleil}&\text{Mur blanc}\\\text{Etoile polaire}&\text{Lune}\\\text{Ecran de télévision}&\text{Vénus}\\\text{Satellite Spot}&\text{Ecran de protection}\\\text{ }&\text{Atmosphère}\\\hline\end{array}$$
Exercice 2
Complétons :
Les sources primaires produisent la lumière qu'elles émettent.
Les sources secondaires sont des objets lumineux éclairés par des sources primaires.
La lumière émise par les sources se propage en ligne droite dans un milieu transparent et homogène.
On traduit ce type de propagation la construction de droites orientées appelées rayons.
Exercice 3
a) Calculons le temps mis par la lumière à nous parvenir
Soit :
$\begin{array}{rcl} t&=&\dfrac{d}{c}\\ \\&=&\dfrac{150.10^{9}}{3.10^{8}}\\ \\&=&5.10^{2}\;s\end{array}$
Ainsi, $\boxed{t=8\;mn\ 33\;s}$
b) Calculons la distance de la terre à la lune
Soit :
$\begin{array}{rcl} d&=&c\times t\\ \\&=&3.10^{8}\times 2.6\\ \\&=&7.810^{8}\;m\end{array}$
Donc, $\boxed{d=7.810^{8}\;m}$
Exercice 4
1) Un milieu transparent est un milieu qui laisse passer la lumière sans la diffuser ni l'absorber (ou très peu), c'est-à-dire que l'on peut distinguer nettement un objet se situant de l'autre côté.
2) Un milieu est homogène s'il possède les même caractéristiques en chacun de ses points (même composition chimique, même température et même pression).
3) Exemples de milieux transparents et homogènes : l'air, verre poli et l'eau
4) Dans un milieu transparent et homogène, la lumière se propage en ligne droite
Exercice 5
Dessinons et orientons le parcours de la lumière afin de décrire au mieux le phénomène de propagation rectiligne de la lumière
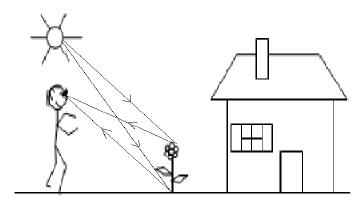
Exercice 6
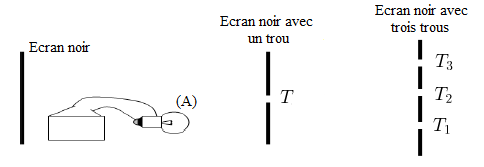
Le faisceau de lumière issu du trou $T$ est un faisceau divergent .
L'observateur peut voir de la lumière à partir de n'importe de quel trou.
Exercice 7
1) La vue arrive aux objets si la lumière les éclaire.
2) Si vous voyez vos pieds c'est qu'ils émettent de la lumière.
3) La lumière éclaire les objets et elle est renvoyée vers l'œil.
4) L'œil voit les objets quand la vue est suffisamment forte pour y arriver : la vue est d'autant plus forte que la lumière ambiante est importante.
Exercice 8
On considère une source ponctuelle $S$, une petite sphère de rayon $r=2\;cm$ et un écran placé à la distance $D=2.0\;m$ de la source $S.$
La sphère est placée à la distance $d=0.5\;m$ de la source ponctuelle de telle façon que l'on puisse voir son ombre portée sur l'écran. La source $S$ et les centres de l'écran et de la sphère sont alignés.
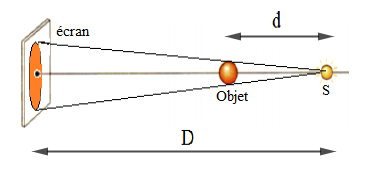
1) Nature géométrique de l'ombre portée sur l'écran : l'ombre portée est un cercle
2) Évaluons les dimensions de cette ombre portée et sa surface.
$-\ $ Diamètre ou hauteur de l'ombre portée, soit : $d_{0}$
$\begin{array}{rcrcl}\dfrac{d_{0}}{D}=\dfrac{2r}{d}&\Rightarrow&d_{0}&=&\dfrac{2r}{d}D\\ \\&\Rightarrow&d_{0}&=&\dfrac{2\times 2}{0.5}\times 2\\ \\&\Rightarrow&d_{0}&=&16\end{array}$
Par suite, $\boxed{d_{0}=16\;cm}$
$-\ $ Rayon de l'ombre portée, soit : $r_{0}$
$\begin{array}{rcl} r_{0}&=&\dfrac{d_{0}}{2}\\ \\&=&\dfrac{16}{2}\\ \\&=&8\end{array}$
Ainsi, $\boxed{r_{0}=8\;cm}$
$-\ $ Surface de l'ombre portée, soit : $S_{0}$
$\begin{array}{rcl} S_{0}&=&\pi r_{0}^{2}\\ \\&=&\pi\times 8^{2}\\ \\&=&2.01\cdot 10^{2}\end{array}$
D'où, $\boxed{S_{0}=2.01\cdot 10^{2}\;cm^{2}}$
3) Conditions pour obtenir sur l'écran la même ombre portée qu'avec la sphère :
L'axe doit passer le centre du disque et le disque doit occuper la même position que la petite sphère
Exercice 9
1) Détermination de la distance entre les surfaces des deux astres.
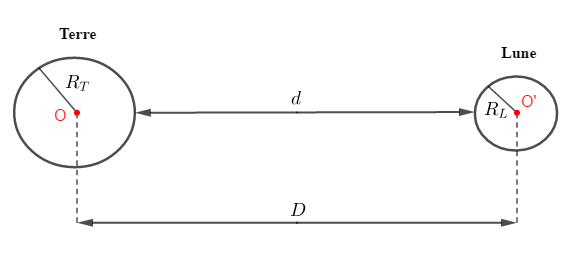
On a :
$\begin{array}{rcrcl} 2d=c\times t&\Rightarrow&d&=&\dfrac{c\times t}{2}\\ \\&\Rightarrow&d&=&\dfrac{3.10^{8\times 2.51}}{2}\\ \\&\Rightarrow&d&=&376.5\cdot 10^{3}\;km\end{array}$
Ainsi, $\boxed{d=376.5\cdot 10^{3}\;km}$
2) Déduisons la distance entre leurs centres.
Soit : $D=d+R_{T}+R_{L}$
A.N : $D=376.5\;10^{3}+6.40\;10^{3}+1.74\;10^{3}=385.10^{3}$
D'où, $\boxed{D=385.10^{3}\;km}$
Exercice 10
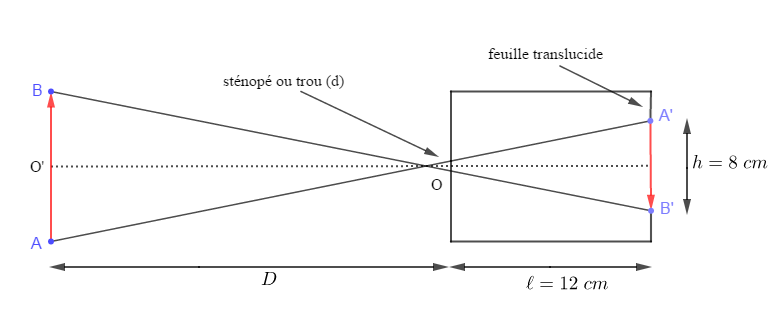
1) Montrons que l'œil de Julien placé derrière la feuille translucide voit une reproduction du filament renversée sur la feuille.
L'image $A'B'$ sur la feuille translucide est bien renversée
Déterminons la taille de l'image $A'B'$
$\begin{array}{rcrcl}\dfrac{A'B'}{AB}=\dfrac{1}{D}&\Rightarrow&A'B'&=&\dfrac{1}{D}\times AB\\ \\&\Rightarrow&A'B'&=&\dfrac{12}{60}\times10\\ \\&\Rightarrow&A'B'&=&2\end{array}$
Par suite, $\boxed{A'B'=2\;cm}$
2) Montrons avec deux rayons issus de $O'$ que le diamètre du trou influe sur la netteté de l'image.
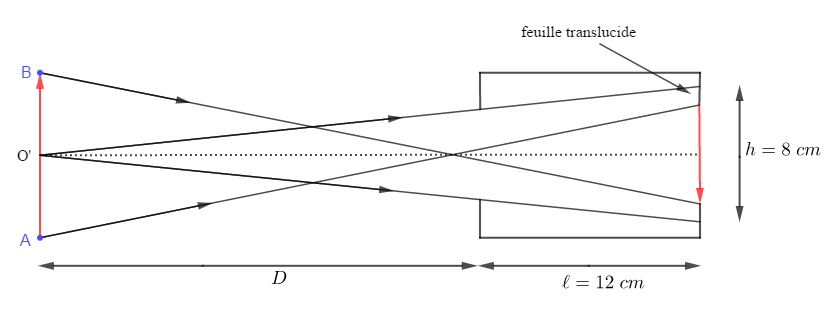
L'image obtenue est constituée du pénombre porté et de l'ombre portée, ce qui la rend floue donc, moins nette
Établissons la relation qui lie la largeur e de l'image à la distance D et aux caractéristiques de la chambre noire $(l\ $ et $\ d)$ puis :
$$\dfrac{e}{l}=\dfrac{d}{D}\Rightarrow e=\dfrac{d}{D}l$$
Calcul de $e$
$e=\dfrac{d}{D}l=\dfrac{1}{60}\times 12=0.2$
D'où, $\boxed{e=0.2\;mm}$

Commentaires
BIKINDOU (non vérifié)
mer, 09/20/2023 - 13:33
Permalien
ACQUERIR DES CONNAISSANCES SUR LA PROPAGATION DE LA LUMIERE
Kone Drissa (non vérifié)
ven, 02/02/2024 - 17:38
Permalien
Mon objectif est de reconnaître mes erreurs pour corriger.
Ajouter un commentaire