Solution des exercices : Réflexion de la lumière - 2nd S
Classe:
Seconde
Exercice 2
1) Énonçons les lois de Descartes relatives à la réflexion de la lumière.
$\centerdot\ $ Le rayon réfléchi est dans le plan d'incidence
$\centerdot\ $ L'angle d'incidence est égal à l'angle de réfraction
2.1) Expliquons pourquoi le miroir donne de l'objet $S$ une image.
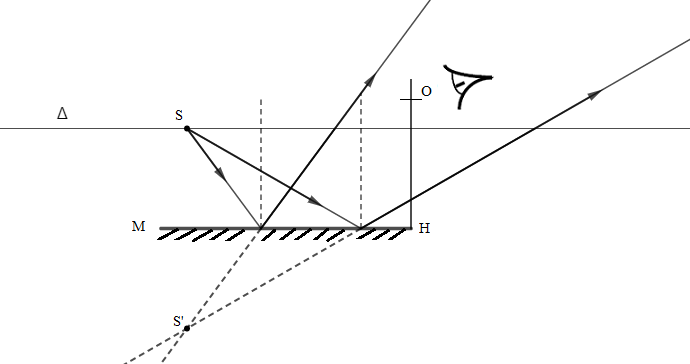
L'image $S'$ obtenue est une image virtuelle dont on peut la voir à travers le miroir
Précisons la position de cette image.
L'image $S’$ est la symétrie de $S$ par rapport au miroir
2.2) Construisons la marche du rayon lumineux issu de $S$ et qui, après réflexion sur le miroir arrive en $O$
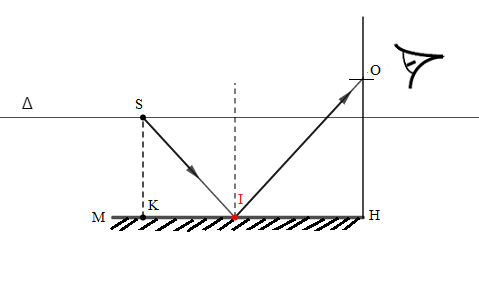
3) Déterminons les positions de $S$ pour lesquelles l'observateur peut voir l'image $S’$ de $S$ en regardant la face du miroir
$\dfrac{KI}{IH}=\dfrac{SK}{OH}\ \Rightarrow\ KI=\dfrac{SK}{OH}IH$
En posant $KI=y\;,\ IH=x$, on obtient :
$$y=\dfrac{1}{1.5}x\ \Rightarrow\ y=0.67x\ \text{ avec, }\ 0<x\leq 2\;m$$
Ainsi, l'ensemble des postions de $S$ est une droite linéaire
Exercice 3
Le miroir $M_{1}M_{2}$ est placé dans le plan perpendiculaire à la figure et contenant les points : $M_{1}(0\;;\ -1.5)\ $ et $\ M_{2}(0\;;\ 3).$
L'œil de l'observateur est placé en $\Omega(3\;;\ 0).$
Plaçons les points $A(3\;;\ 3)\;,\ B(3\;;\ 6)\ $ et $\ C(1.5\;;\ 6)$
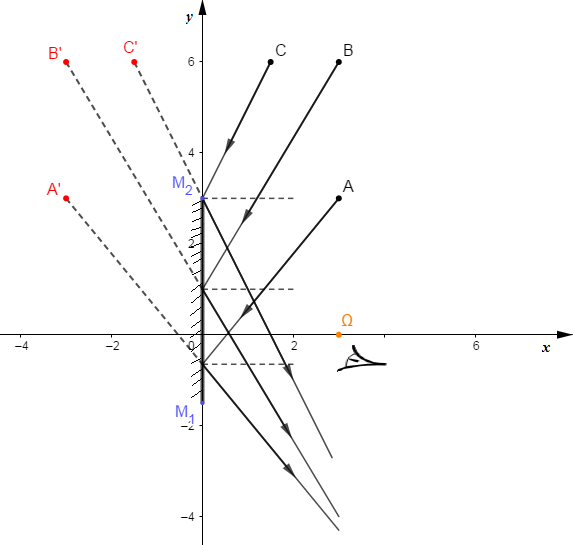
L'œil peut voir les images $A'\;,\ B'\ $ et $\ C'$ des points $A\;,\ B\ $ et $\ C$

Commentaires
jack (non vérifié)
sam, 05/28/2022 - 15:16
Permalien
y
Mourtallah Diallo (non vérifié)
lun, 01/02/2023 - 21:20
Permalien
Réussir à mes études
Ajouter un commentaire