Solution des exercices sur les Masses : masse volumique et densité - 4e
Classe:
Quatrième
Exercice 1
Complétons le texte ci-dessous par les mots, groupes de mots ou symboles suivants :
gramme, masses marquées, le centigramme, quintal, décakilogramme, masse, le kilogramme, kg, décroissant, sous multiple, $t$, $1000$, hectogramme, décagramme.
$\centerdot\ $ La balance permet de déterminer la masse d'un objet.
$\centerdot\ $ La masse a pour unité internationale le kilogramme de symbole $kg$
$\centerdot\ $ Le décigramme est sous multiple du kilogramme alors que la tonne, de symbole $t$ en est un multiple et vaut $1000\;kg.$
$\centerdot\ $ Les autres sous multiples sont : hectogramme, décagramme, gramme, le centigramme.
$\centerdot\ $ Les multiples restant sont : quintal et décakilogramme
$\centerdot\ $ Avec une balance Roberval, lors de la pesée, on utilise des masses marquées pour rééquilibrer la balance.
$\centerdot\ $ Les masses marquées sont posées dans l'ordre décroissant.
Exercice 2
Encadrons la (ou les ) lettre(s) correspondante(s)
1) La masse d'un objet peut s'exprimer en :
$\boxed{\text{a) kilogramme}}$
b) mètre cube ;
c) kilogramme par mètre cube ;
$\boxed{\text{d) gramme}}$
2) La tonne est :
a) l'unité du système international de masse
$\boxed{\text{b) un multiple du kilogramme}}$
c) un sous multiple du kilogramme
$\boxed{\text{d) égale à mille kilogrammes}}$
3) Pour déterminer la masse d'une voiture, on utilise :
a) une balance Roberval
b) une bascule
$\boxed{\text{c) un pont bascule}}$
4) La masse d'un objet à Dakar est $15\;kg.$
Sa masse au nord de la France sera :
a) plus grande ;
b) plus petite ;
$\boxed{\text{c) la même}}$
Exercice 3
1) En utilisant les puissances de 10, convertissons puis donnons l'écriture scientifique :
Rappel : On peut se référer sur le tableau suivant :
$$\begin{array}{|c|c|c|c|c|c|c|}\hline kg&hg&dag&g&dg&cg&mg\\ \hline&&&&&&\\ \hline\end{array}$$
L'écriture scientifique d'un nombre $x$ est donnée par :
$$x=a\cdot 10^{p}\quad\text{avec }\ 1\leq a\leq 10\ \text{ et }\ p\in\mathbb{Z}$$
a) On a : $1\;hg=100\;g=10^{2}\;g$
Donc, $14\;hg=14\cdot 10^{2}\;g$
L'écriture scientifique est $1.4\cdot 10^{3}\;g$
b) On sait que : $1\;dag=0.01\;kg=10^{-2}\;kg$
Alors, $25\;dag=25\cdot 10^{-2}\;kg$
En écriture scientifique, on obtient : $25\;dag=2.5\cdot 10^{-1}\;kg$
c) On a : $1\;mg=0.001\;g=10^{-3}\;g$
Ainsi, $1950\;mg=1950\cdot 10^{-3}\;g$
L'écriture scientifique est donnée par : $1950\;mg=1.95\cdot 10^{0}\;g\ (=1.95\;g)$
d) Soit : $1\;kg=1000\;g=10^{3}\;g$
Donc, $2.5\;kg=2.5\cdot 10^{3}\;g$
L'écriture scientifique est aussi donnée par $2.5\cdot 10^{3}\;g$
e) On a : $1\;g=1000\;mg=10^{3}\;mg$
Alors, $150\;g=150\cdot 10^{3}\;mg$
Ce qui donne, en écriture scientifique : $150\;g=1.5\cdot 10^{5}\;mg$
f) On sait que : $1\;cg=10\;mg=10^{1}\;mg\ $ et $\ 1\;cg=0.0001\;hg=10^{-4}\;hg$
Par suite, $27\;cg=27\cdot 10^{1}\;mg\ $ et $\ 27\;cg=27\cdot 10^{-4}\;hg$
En écriture scientifique, on obtient :
$27\;cg=2.7\cdot 10^{2}\;mg\ $ et $\ 27\;cg=2.7\cdot 10^{-3}\;hg$
2) On a déterminé la masse d'un objet à l'aide d'une balance Roberval.
Sachant que la masse trouvée est de $m=278\;g$, les masses marquées sur le plateau à la fin de la pesée sont :
$$200\;g\;;\quad 50\;g\;;\quad 20\;g\;;\quad 5\;g\;;\quad 2\;g\;;\quad 1\;g$$
Exercice 4
Complétons le texte ci-dessous par les mots, groupes de mots ou symboles suivants :
le volume, kilogramme par mètre cube, une constante, masse volumique, variable, $kg.m^{-3}$, la masse.
$\centerdot\ $ La masse de l'unité de volume est appelé masse volumique.
$\centerdot\ $ La masse volumique s'exprime en kilogramme par mètre cube de symbole $kg.m^{-3}.$
$\centerdot\ $ Pour calculer la masse volumique d'une substance ou d'un corps, on fait le rapport entre la masse et le volume.
$\centerdot\ $ La masse volumique d'un corps pur est une constante alors qu'elle est variable pour un mélange.
Exercice 5
Encadrons la lettre correspondant à la (ou les) bonne (s) réponse (s) dans les questions suivantes :
1) La masse volumique $\rho\text{ (rho)}$ d'une substance de masse $m$ et de volume $V$ a pour expression :
$\boxed{\text{a) }\rho=\dfrac{m}{V}}$ ;
b) $\rho=\dfrac{V}{m}$ ;
c) $\rho=m\;V$
2) A partir de l'expression de la masse volumique, la masse s'obtient par :
a) $m=\dfrac{\rho}{V}$
b) $m=\dfrac{V}{\rho}$
$\boxed{\text{c) }m=\rho\;V}$
3) A partir de l'expression de la masse volumique, le volume s'obtient par :
a) $V=m\rho$
$\boxed{\text{b) }V=\dfrac{m}{\rho}}$
c) $V=\dfrac{\rho}{m}$
Exercice 6
1) La masse d'un volume $V=0.5\;l$ d'essence est $m=0.35\;kg.$
a) L'expression de la masse volumique est donnée par :
$$\boxed{\rho=\dfrac{m}{V}}$$
b) Calculons la masse volumique de l'essence :
$-\ \ $ en $kg.l^{-1}$
On a : $\rho=\dfrac{m}{V}\ $ avec $m$ exprimée en $kg$ et $V$ exprimé en $l$
A.N : $\rho=\dfrac{0.35}{0.5}=0.7$
Donc, $\boxed{\rho=0.7\;kg.l^{-1}}$
$-\ \ $ en $kg.m^{-3}$
On sait que : $\rho=\dfrac{m}{V}$
Comme le volume $V$ est exprimé en litre alors, convertissons le en $m^{3}.$
On a : $1\;l=10^{-3}\;m^{3}\ $ donc, $0.5\;l=0.5\cdot 10^{-3}\;m^{3}$
Par suite,
$\begin{array}{rcl}\rho&=&\dfrac{0.35}{0.5\cdot 10^{-3}}\\ \\&=&\dfrac{0.35\cdot 10^{3}}{0.5}\\ \\&=&\dfrac{350}{0.5}\\ \\&=&700 \end{array}$
D'où, $\boxed{\rho=700\;kg.m^{-3}}$
$-\ \ $ en $g.l^{-1}$
On a : $\rho=\dfrac{m}{V}$
Or, la masse est exprimée en kilogramme donc, convertissons la en gramme.
Soit : $1\;kg=10^{3}\;g\ $ alors, $0.35\;kg=0.35\cdot 10^{3}\;g=350\;g$
Donc, $\rho=\dfrac{350}{0.5}=700$
Ainsi, $\boxed{\rho=700\;g.l^{-1}}$
2) Calculons le volume en $dm^{3}$ de $58.5\;kg$ de fer si la masse volumique du fer est $7.8\;g.cm^{-3}$
L'expression du volume étant donnée par :
$$\boxed{V=\dfrac{m}{\rho}}$$
Or, la masse volumique du fer est exprimée en $g.cm^{-3}$ et la masse est en kilogramme donc, convertissons la masse en gramme.
Soit : $1\;kg=10^{3}\;g\ $ alors, $58.5\;kg=58.5\cdot 10^{3}\;g$
Ainsi,$V=\dfrac{58.5\cdot 10^{3}}{7.8}=7500\;cm^{3}$
Ce volume trouvé étant exprimé en $cm^{3}$ alors, convertissons le en $dm^{3}.$
Soit : $1\;cm^{3}=10^{-3}\;dm^{3}\ $ alors, $7500\;cm^{3}=7500\cdot 10^{-3}\;dm^{3}=7.5\;dm^{3}$
Par suite, $\boxed{V=7.5\;dm^{3}}$
3) Déterminons la masse de $350\;cm^{3}$ d'aluminium sachant que la masse volumique de l'aluminium est $2700\;g.dm^{-3}.$
Pour calculer la masse on utilise son expression donnée par :
$$\boxed{m=\rho.V}$$
$\rho$ étant exprimée en $g.dm^{-3}$ alors, convertissons le volume $V$ en $dm^{-3}$
On a : $1\;cm^{3}=10^{-3}\;dm^{3}\ $ donc, $350\;cm^{3}=350\cdot 10^{-3}\;dm^{3}=0.35\;dm^{3}$
Ainsi, $m=2700\times 0.35=945$
D'où, $\boxed{m=945\;g}$
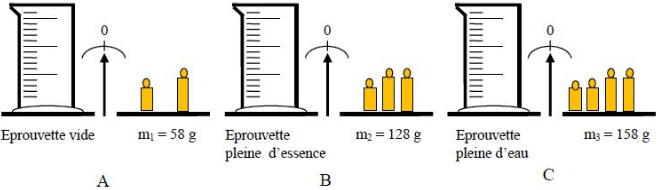
Exercice 7
On veut déterminer la masse volumique de l'essence.
Les opérations de pesage $A\;,\ B\text{ et }C$ ci-dessous ont été réalisées :

Répondons à cette série de questions en choisissant la bonne réponse dans chaque cas.
1) Dans l'opération $A$ on a pesé la masse de :
$\boxed{\text{a) Éprouvette}}$
b) Essence
c) Eau
2) Dans l'opération $B$ on a pesé la masse de :
a) Essence
$\boxed{\text{b) Éprouvette plus essence}}$
c) Eau
3) Dans l'opération $C$ on a pesé la masse de :
a) Eau
$\boxed{\text{b) Éprouvette plus eau}}$
c) Éprouvette
La masse de l'essence est :
a) $m_{ess}=m_{3}-m_{1}$
b) $m_{ess}=m_{3}-m_{2}$
$\boxed{\text{c) }m_{ess}=m_{2}-m_{1}}$
5) La masse de l'eau est :
$\boxed{\text{a) }m_{eau}=m_{3}-m_{1}}$
b) $m_{eau}=m_{3}-m_{2}$
c) $m_{eau}=m_{2}-m_{1}$
6) La masse volumique de l'eau étant de $1\;g.cm^{-3}$ alors le volume de l'eau est :
a) $30\;cm^{3}$
$\boxed{\text{b) }100\;cm^{3}}$
c) $70\;cm^{3}$
7) L'essence et l'eau ont :
$\boxed{\text{a) des volumes égaux}}$
b) des volumes différents
8) En s'aidant des réponses données dans les différentes questions, calculons la masse volumique de l'essence.
On sait que :
$$\rho_{ess}=\dfrac{m_{ess}}{V_{ess}}$$
Or, d'après question 4) $m_{ess}=m_{2}-m_{1}$
De plus $V_{eau}=V_{ess}$, d'après la question 7).
Ainsi, $\rho_{ess}=\dfrac{m_{2}-m_{1}}{V_{eau}}\ $ avec $V_{eau}=100\;cm^{3}$, d'après la question 6).
A.N : $\rho_{ess}=\dfrac{128-58}{100}=0.7$
Par suite, $\boxed{\rho_{ess}=0.7\;g.cm^{-3}}$
Exercice 8
Le diamant est du carbone pur de masse volumique de $3500\;kg.m^{-3}$
Sa densité du diamant par rapport au verre est de 1.4
Calculons la masse volumique $\rho_{_{\text{verre}}}$ du verre.
Soit $d_{_{\text{diamant}}}$ la densité du par rapport au verre.
On a : $d_{_{\text{diamant}}}=\dfrac{\rho_{_{\text{diamant}}}}{\rho_{_{\text{verre}}}}$
Ce qui donne : $d_{_{\text{diamant}}}\times\rho_{_{\text{verre}}}=\rho_{_{\text{diamant}}}$
Par suite :
$$\rho_{_{\text{verre}}}=\dfrac{\rho_{_{\text{diamant}}}}{d_{_{\text{verre}}}}$$
A.N : $\rho_{_{\text{verre}}}=\dfrac{3500}{1.4}=2500$
D'où, $\boxed{\rho_{_{\text{verre}}}=2500\;kg.m^{-3}}$
Exercice 9
La densité du lait est de 1.03 or, $d_{_{\text{lait}}}=\dfrac{\rho_{_{\text{lait}}}}{\rho_{_{\text{eau}}}}$
Donc, $\dfrac{\rho_{_{\text{lait}}}}{\rho_{_{\text{eau}}}}=1.03$
Par suite, $\rho_{_{\text{lait}}}=1.03\times\rho_{_{\text{eau}}}$
Comme $1.03\times\rho_{_{\text{eau}}}>1\times\rho_{_{\text{eau}}}=\rho_{_{\text{eau}}}$ alors,
$$\rho_{_{\text{lait}}}>\rho_{_{\text{eau}}}$$
Ce qui signifie que le lait est plus dense que l'eau.
Calculons la masse de $1.5\;L$ de lait.
On a : $\rho_{_{\text{lait}}}=\dfrac{m_{_{\text{lait}}}}{V_{_{\text{lait}}}}$
Donc, $m_{_{\text{lait}}}=\rho_{_{\text{lait}}}\times V_{_{\text{lait}}}$
Comme $\rho_{_{\text{lait}}}=1.03\times\rho_{_{\text{eau}}}$ alors,
$$m_{_{\text{lait}}}=1.03\times\rho_{_{\text{eau}}}\times V_{_{\text{lait}}}$$
A.N : $m_{_{\text{lait}}}=1.03\times 1000\times 1.5=1545$
D'où, $\boxed{m_{_{\text{lait}}}=1545\;g}$
On peut aussi choisir $\rho_{_{\text{eau}}}=1\;kg.l^{-1}$ dans ce cas, on aura :
$m_{_{\text{lait}}}=1.03\times 1\times 1.5=1.545\;kg$
Exercice 10
Une bouteille de volume $5\;l$ a une masse de $2.7\;kg$, lorsqu'elle est à moitié remplie d'eau.
Sa masse est de $4.145\;kg$ si elle est remplie d'alcool.
1) Calculons la masse de la bouteille vide sachant que la masse volumique de l'eau est de $1000\;kg.m^{-3}$
Soit :
$\cdot\ \ m_{_{e}}$ la masse d'eau contenue dans la bouteille
$\cdot\ \ m_{_{b}}$ la masse de la bouteille vide
$\cdot\ \ m_{_{(b+e)}}$ la masse totale de la bouteille contenant de l'eau
On a : $m_{_{(b+e)}}=m_{_{e}}+m_{_{b}}$
Donc, $m_{_{b}}=m_{_{(b+e)}}-m_{_{e}}$
Or, $m_{_{e}}=\rho_{_{e}}\times V_{_{e}}$
Par suite,
$$\boxed{m_{_{b}}=m_{_{(b+e)}}-\rho_{_{e}}\times V_{_{e}}}$$
La bouteille étant à moitié remplie d'eau donc, $V_{_{e}}=\dfrac{5}{2}=2.5\;l$
Application numérique : $m_{_{b}}=2.7-(1000\times 2.5\;10^{-3})=0.2$
D'où, $\boxed{m_{_{b}}=0.2\;kg}$
2) Calculons la masse de l'alcool
En considérant $m_{_{a}}$ la masse de l'alcool contenu dans la bouteille et $m_{_{(b+a)}}$ la masse totale de la bouteille contenant de l'alcool, on obtient : $m_{_{(b+a)}}=m_{_{a}}+m_{_{b}}$
Ainsi,
$$\boxed{m_{_{a}}=m_{_{(b+a)}}-m_{_{b}}}$$
A.N : $m_{_{a}}=4.145-0.2=3.945$
D'où, $\boxed{m_{_{a}}=3.945\;kg}$
En déduisons sa masse volumique, $\rho_{_{a}}.$
On sait que : $\rho_{_{a}}=\dfrac{m_{_{a}}}{V_{_{a}}}$
A.N : $\rho_{_{a}}=\dfrac{3.945}{5\;10^{-3}}=789$
Ainsi, $\boxed{\rho_{_{a}}=789\;kg.m^{-3}}$
Exercice 11
La densité de l'or par rapport au mercure est de $1.42$
Calculons la masse volumique $\rho_{_{or}}$ de l'or en $kg.dm^{-3}$ sachant que celle du mercure est $13.6\;g.ml^{-1}$
On a : $d_{_{or}}=\dfrac{{\rho}_{_{or}}}{{\rho}_{_{mercure}}}$
Donc, $\rho_{_{or}}=d_{_{or}}\times\rho_{_{mercure}}\ $ avec $d_{_{or}}=1.42$
Application numérique : $\rho_{_{or}}=1.42\times 13.6=19.312$
D'où, $\rho_{_{or}}=19.312\;g.ml^{-1}$
Convertissons en $kg.dm^{-3}$
On a : $\dfrac{1\;g}{1\;ml}=\dfrac{10^{-3}\;kg}{10^{-3}\;dm^{3}}=\dfrac{1\;kg}{1\;dm^{3}}$
Ainsi, $19.312\;g.ml^{-1}=19.312\;kg.dm^{-3}$
Par suite, $\boxed{\rho_{_{or}}=19.312\;kg.dm^{-3}}$
On constate que $\rho_{_{or}}>\rho_{_{mercure}}$ ou encore que $d_{_{or}}>1.$ Ce qui veut dire que l'or est plus dense que le mercure.
Par conséquent, l'or ne peut flotter dans le mercure.
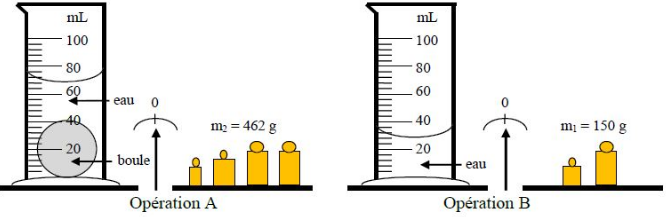
Exercice
Pour déterminer la masse volumique d'une boule on a effectué les opérations $A\ $ et $\ B$ suivantes :

1) A partir du schéma ci-dessus, déduisons la masse de la boule ainsi que son volume.
$-\ $ masse de la boule
D'après l'opération $A$, on a : $m_{_{eau}}+m_{_{boule}}=462\;g$
Donc, $m_{_{boule}}=462\;g-m_{_{eau}}$
Or, $\ m_{_{eau}}=150\;g$, d'après l'opération $B$
Par suite, $m_{_{boule}}=462-150=312$
D'où, $\boxed{m_{_{boule}}=312\;g}$
$-\ $ volume de la boule
En observant l'opération $A$, on obtient : $V_{_{eau}}+V_{_{boule}}=68\;ml$
Ce qui donne, $V_{_{boule}}=68\;ml-V_{_{eau}}$
Comme $V_{_{eau}}=28\;ml$, d'après l'opération $B$ alors, $V_{_{boule}}=68-28=40$
Ainsi, $\boxed{V_{_{boule}}=40\;ml}$
2) Calculons la masse volumique $\rho_{_{boule}}$ de la boule.
On a : $\rho_{_{boule}}=\dfrac{m_{_{boule}}}{V_{_{boule}}}$
Application numérique : $\rho_{_{boule}}=\dfrac{312}{40}=7.8$
D'où, $\boxed{\rho_{_{boule}}=7.8\;g.ml^{-1}}$

Exercice 12
On veut déterminer la nature d'un métal inconnu $X.$
Pour ce faire, on cherche à déterminer sa masse volumique en réalisant les opérations $A\;,\ B\ $ et $\ C$ de pesées décrites dans les schémas ci-dessous :

Après avoir bien observé les schémas, déterminer :
1) Déterminons la masse du métal inconnu $X$
Dans l'opération $B$, on a : $m_{2}=m_{_{X}}+m_{_{E}}$ où $m_{_{E}}$ est la masse de l'éprouvette pleine d'eau.
Donc, $m_{_{X}}=m_{2}-m_{_{E}}$
Comme $m_{_{E}}=m_{1}$, d'après l'opération $A$ alors,
$$m_{_{X}}=m_{2}-m_{1}$$
Application numérique : $m_{_{X}}=567-450=117$
Ainsi, $\boxed{m_{_{X}}=117\;g}$
2) Déterminons la masse de l'eau remplacée par le métal $X$ lorsqu'il est introduit dans le bêcher.
Dans l'opération $C$, en introduisant le métal $X$ dans le bêcher, une partie de l'eau sera remplacée par la masse de ce métal.
Soit $m_{_{r}}$ cette masse d'eau remplacée par la masse du métal $X$
Donc, tout se passe comme si dans l'opération $B$ on a enlevé un volume d'eau de masse $m_{_{r}}$ pour obtenir une masse finale $m_{3}$
Ce qui se traduit par : $m_{2}-m_{_{r}}=m_{3}$
Par suite :
$$m_{_{r}}=m_{2}-m_{3}$$
A.N : $m_{_{r}}=567-552=15$
D'où, $\boxed{m_{_{r}}=15\;g}$
3) Déterminons le volume du métal si $\rho_{e}=1\;g.ml^{-1}$
Le volume du métal $(V_{_{X}})$ est équivalent au volume d'eau $(V_{_{e}})$ qu'il a remplacée.
Or, on sait que : $\rho_{e}=\dfrac{m_{_{r}}}{V_{_{e}}}$
Donc, $\rho_{e}\times V_{_{e}}=m_{_{r}}$
Ainsi, $V_{_{e}}=\dfrac{m_{_{r}}}{{\rho}_{e}}$
Par suite :
$$V_{_{X}}=\dfrac{m_{_{r}}}{\rho_{_{e}}}$$
A.N : $V_{_{X}}=\dfrac{15}{1}=15$
D'où, $\boxed{V_{_{X}}=15\;ml}$
4) Calculons la masse volumique $(\rho_{_{X}})$ du métal inconnu $X$
On a :
$$\rho_{_{X}}=\dfrac{m_{_{X}}}{V_{_{X}}}$$
A.N : $\rho_{_{X}}=\dfrac{117}{15}=7.8$
Donc, $\boxed{\rho_{_{X}}=7.8\;g.ml^{-1}}$
5) En utilisant le tableau ci-dessous, donnons en justifiant la nature du métal inconnu $X.$
$$\begin{array}{|c|c|c|c|} \hline \text{Métaux}&\text{Aluminium}&\text{Zinc}&\text{Fer}\\ \hline \text{Masse volumique}&2700\;kg.m^{-3}&7100\;kg.m^{-3}&7800\;kg.m^{-3}\\ \hline \end{array}$$
D'après le tableau, on peut dire que le métal $X$ est du fer.
En effet, la masse volumique fer est de $7800\;kg.m^{-3}$
Convertissons cette masse volumique en $g.ml^{-1}$
On a : $1\;kg.m^{-3}=\dfrac{1\;kg}{1\;m^{3}}=\dfrac{10^{3}\;g}{10^{6}\;ml}=10^{-3}\;g.ml^{-1}$
Donc, $1\;kg.m^{-3}=10^{-3}\;g.ml^{-1}$
Par suite :
$\begin{array}{rcl} 7800\;kg.m^{-3}&=&7800\times 10^{-3}\;g.ml^{-1}\\&=&7.8\;g.ml^{-1}\end{array}$
Ainsi, $\rho_{_{fer}}=\rho_{_{X}}$
Par conséquent, le métal $X$ est du fer.
6) Calculons la densité $(d_{_{X}})$ du métal $X$ par rapport à l'huile de masse volumique $\rho_{_{H}}=920\;g.l^{-1}$
On a :
$$d_{_{X}}=\dfrac{\rho_{_{X}}}{\rho_{_{H}}}$$
avec $\rho_{_{X}}=7.8\;g.ml^{-1}=7800\;g.l^{-1}$
A.N : $d_{_{X}}=\dfrac{7800}{920}=8.478$
Donc, $\boxed{d_{_{X}}=8.478}$
Exercice 13 : Maitrise de connaissances
Recopions et complétons les phrases suivantes :
La masse d'un corps est une grandeur physique qu'on peut mesurer à l'aide d'une balance.
Elle est exprimée en kilogramme dans le Système International d' Unités.
La masse volumique d'un corps solide est la masse de ce corps par unité de volume dans le Système International d'unités, la masse volumique est exprimée en kilogramme par mètre cube que l'on note $kg.m^{-3}$
Exercice 14
Répondons par Vrai $(V)$ ou faux $(F)$
1) Si deux corps ont le même volume, celui qui a la plus grande masse a la plus grande masse volumique.$\quad(V)$
2) Si deux corps ont la même masse, celui ayant la masse volumique la plus faible occupe le plus petit volume.$\quad(F)$
3) Deux objets formés de matériaux différents et qui ont la même masse ont des volumes différents.$\quad(V)$
4) La densité est donnée par le même nombre que la masse volumique exprimée en $g.l^{-1}\quad(F)$
Exercice 15 : Le bon choix
Encadrons la réponse correcte.
La masse d'un objet est mesurée avec :
$\centerdot\ $ une éprouvette graduée
$\centerdot\ \boxed{\text{une balance}}$
$\centerdot\ $ un masse-mètre.
$\centerdot\ $ un dynamomètre

Exercice 16 : Types de balance
Donnons le nom de chacune des balances puis indiquons un domaine d'activités où est utilisée chacune d'elle.

$$\begin{array}{|c|c|l|}\hline N^{\circ}&\text{Noms}&\text{Domaine d'activité}\\ \hline 1&\text{balance}&\text{utilisée dans le commerce en détail}\\&\text{mécanique}&\text{des denrées alimentaires}\\ \hline 2&\text{trébuchet}&\text{utilisé plus couramment par les}\\&&\text{bijoutiers}\\ \hline 3&\text{bascule}&\text{utilisée par les grossistes pour}\\&&\text{peser de grandes quantités}\\ \hline 4&\text{balance}&\text{utilisée dans le commerce en détail}\\&\text{Roberval}&\text{des denrées alimentaires}\\ \hline 5&\text{balance}&\text{utilisée dans les laboratoires}\\&\text{numérique}&\\ \hline 6&\text{balance}&\text{utilisée par les bouchers}\\&\text{romaine}&\\ \hline\end{array}$$
Exercice 17 : Conversion d'unités
Convertissons :
$\centerdot\ 12.5\;t$ en $kg$
On a : $1\;t=1000\;kg$
Donc, $12.5\;t=12.5\times 1000\;kg=12500\;kg$
$\centerdot\ 3.9\;g$ en $kg$
On sait que : $1\;g=10^{-3}\;kg$
Donc, $3.9\;g=3.9\times 10^{-3}\;kg=3.9\;10^{-3}\;kg$
$\centerdot\ 97.8\;kg.l^{-1}$ en $g.cm^{-3}$
On va donc convertir les $kg$ en $g$ et les $l$ en $cm^{3}$
On a : $1\;kg=10^{3}\;g$ et $1\;l=10^{3}\;cm^{3}$
Alors,
$\begin{array}{rcl} 1\;kg.l^{-1}=\dfrac{1\;kg}{1\;l}&=&\dfrac{10^{3}\;g}{10^{3}\;cm^{3}}\\ \\&=&\dfrac{1\;g}{1\;cm^{3}}\\ \\&=&1\;g.cm^{-3}\end{array}$
Donc, $1\;kg.l^{-1}=1\;g.cm^{-3}$
D'où, $97.8\;kg.l^{-1}=97.8\;g.cm^{-3}$
$\centerdot\ 0.25\;kg.m^{-3}$ en $kg.l^{-1}$
Dans ce cas on va juste convertir les $m^{3}$ en $l$
On a : $1\;m^{3}=1000\;l=10^{3}\;l$
Donc,
$\begin{array}{rcl} 1\;kg.m^{-3}=\dfrac{1\;kg}{1\;m^{3}}&=&\dfrac{1\;kg}{10^{3}\;l}\\ \\&=&\dfrac{1}{10^{3}}kg.l^{-1}\\ \\&=&10^{-3}\;kg.l^{-1}\end{array}$
Ainsi, $1\;kg.m^{-3}=10^{-3}\;kg.l^{-1}$
Par suite, $0.25\;kg.m^{-3}=0.25\times 10^{-3}\;kg.l^{-1}=25\;10^{-5}\;kg.l^{-1}$
$\centerdot\ 3.86\;kg.m^{-3}$ en $g.cm^{-3}$
On sait que : $1\;kg=10^{3}\;g$ et $1\;m^{3}=10^{6}\;cm^{3}$
Alors,
$\begin{array}{rcl} 1\;kg.m^{-3}=\dfrac{1\;kg}{1\;m^{3}}&=&\dfrac{10^{3}\;g}{10^{6}\;cm^{3}}\\ \\&=&\dfrac{10^{3}}{10^{6}}g.cm^{-3}\\ \\&=&10^{-3}\;g.cm^{-3}\end{array}$
Donc, $1\;kg.m^{-3}=10^{-3}\;g.cm^{-3}$
Par suite, $3.86\;kg.m^{-3}=3.86\times 10^{-3}\;g.cm^{-3}=3.86\;10^{-3}\;g.cm^{-3}$
Exercice 18 : Ordres de grandeurs de masses
Relions, à l'aide d'une flèche, chaque corps à l'ordre de grandeurs masse.
$$\begin{array}{|lcl|}\hline \text{Cheveu}&\longrightarrow&0.1\;mg\\ \hline\text{Mouche}&\longrightarrow&20\;mg\\ \hline\text{La Terre}&\longrightarrow&6\;10^{24}\;kg\\ \hline 1\;l\text{ d'air}&\longrightarrow&1.3\;g\\ \hline 1\;l\text{ d'eau}&\longrightarrow&1\;kg\\ \hline\text{Homme adulte}&\longrightarrow&75\;kg\\ \hline \text{Eléphant}&\longrightarrow&3\;t\\ \hline\text{Le soleil}&\longrightarrow&1.989\;10^{30}\;kg\\ \hline\end{array}$$
Exercice 19 : Calcul de masse volumique
1) Le volume occupé par $0.46\;kg$ d'huile est $0.5\;l$
Calculons la masse volumique de l'huile en $kg.l^{-1}$ en $kg.m^{-3}\ $ et en $g.l^{-1}$
On sait que :
$$\rho=\dfrac{m}{V}$$
Or, $m=0.46\;kg\ $ et $\ V=0.5\;l$
Donc, $\rho=\dfrac{0.46}{0.5}=0.92$
Par suite, $\boxed{\rho=0.92\;kg.l^{-1}}$
Pour mettre ce résultat en $kg.m^{-3}$, on peut simplement exprimer le volume en $m^{3}$
On a : $1\;l=10^{-3}\;m^{3}$ donc, $0.5\;l=0.5\times 10^{-3}\;m^{3}$
Ainsi, $\rho=\dfrac{0.46}{0.5\;10^{-3}}=\dfrac{0.46}{0.5}10^{3}=0.92\;10^{3}$
D'où, $\boxed{\rho=920\;kg.m^{-3}}$
Pour exprimer la masse volumique en $g.l^{-1}$, on va devoir convertir la masse en gramme.
Soit : $1\;kg=10^{3}\;g$ donc, $0.46\;kg=0.46\times 10^{3}\;g=460\;g$
Par suite, $\rho=\dfrac{460}{0.5}=920$
D'où, $\boxed{\rho=920\;g.l^{-1}}$
2) Calculons en $dm^{3}$ le volume d'une masse $m=96.5\;kg$ d'or si la masse volumique de l'or est $19.3\;g.cm^{-3}$
L'expression du volume est donnée par :
$$V=\dfrac{m}{\rho}$$
Or, pour cette question, $\rho$ est en $g.cm^{-3}$ et $m$ en $kg$ donc, nous allons convertir la masse en gramme.
Comme $1\;kg=10^{3}\;g$ alors, $96.5\;kg=96.5\times 10^{3}\;g$
Par suite, $V=\dfrac{96.5\;10^{3}}{19.3}=5\;10^{3}$
Ainsi, $V=5\;10^{3}\;cm^{3}$
Convertissons le résultat en $dm^{3}$
On sait que : $1\;cm^{3}=10^{-3}\;dm^{3}$
Alors, $5\;10^{3}\;cm^{3}=5\;10^{3}\times 10^{-3}\;dm^{3}=5\;dm^{3}$
Donc, $\boxed{V=5\;dm^{3}}$
3) Déterminons la masse de $350\;cm^{3}$ d'aluminium si sa masse volumique est $2700\;g.dm^{-3}$
L'expression de la masse est donnée par :
$$m=\rho\times V$$
Dans cette question, $\rho$ est exprimée en $g.dm^{-3}$ et $V$ en $cm^{3}$ donc, on doit convertir le volume en $dm^{3}$ pour trouver la masse en gramme.
On a : $1\;cm^{3}=10^{-3}\;dm^{3}$ donc, $350\;cm^{3}=350\times 10^{-3}\;dm^{3}$
Ainsi, $m=2700\times 350\times 10^{-3}=945$
D'où, $\boxed{m=945\;g}$
Exercice 20
Des mesures de masses et de volumes effectuées sur plusieurs corps ont conduit au tableau de mesure suivant.
$$\begin{array}{|l|c|c|c|c|c|c|} \hline\text{Corps}&A&B&C&D&E&F\\ \hline m(g)&22.4&46.2&66.8&90.4&114.9&133.0\\ \hline V(cm^{3})&2.0&4.1&5.9&8.0&14.7&17.0\\ \hline \end{array}$$
Déterminons alors les corps qui sont constitués de la même substance.
Pour cela, nous allons chercher les masses volumiques de ces différents corps.
Il faut noter que chaque corps pur est caractérisé par des constantes physiques (température de fusion et d'ébullition, masse volumique).
Donc, deux corps constitués par la même substance ont les mêmes constantes physiques.
L'expression de la masse volumique étant donnée par :
$$\rho=\dfrac{m}{V}$$
alors :
$\rho_{_{A}}=\dfrac{m_{_{A}}}{V_{_{A}}}=\dfrac{22.4}{2}=11.2$
$\rho_{_{B}}=\dfrac{m_{_{B}}}{V_{_{B}}}=\dfrac{46.2}{4.1}=11.2$
$\rho_{_{C}}=\dfrac{m_{_{C}}}{V_{_{C}}}=\dfrac{66.8}{5.9}=11.3$
$\rho_{_{D}}=\dfrac{m_{_{D}}}{V_{_{D}}}=\dfrac{90.4}{8.0}=11.3$
$\rho_{_{E}}=\dfrac{m_{_{E}}}{V_{_{E}}}=\dfrac{114.9}{14.7}=7.8$
$\rho_{_{F}}=\dfrac{m_{_{F}}}{V_{_{F}}}=\dfrac{133}{17}=7.8$
En regroupant le tout dans un tableau, on obtient :
$$\begin{array}{|l|c|c|c|c|c|c|} \hline\text{Corps}&A&B&C&D&E&F\\ \hline m(g)&22.4&46.2&66.8&90.4&114.9&133.0\\ \hline V(cm^{3})&2.0&4.1&5.9&8.0&14.7&17.0\\ \hline\rho(g.cm^{-3})&11.2&11.2&11.3&11.3&7.8&7.8\\ \hline\end{array}$$
On constate alors :
$\centerdot\ \rho_{_{A}}=\rho_{_{B}}$ donc, les corps $A\ $ et $\ B$ sont constitués par la même substance.
$\centerdot\ \rho_{_{C}}=\rho_{_{D}}$ ce qui signifie que les corps $C\ $ et $\ D$ sont constitués par la même substance.
$\centerdot\ \rho_{_{E}}=\rho_{_{F}}$ ce qui veut dire que les corps $E\ $ et $\ F$ sont constitués par la même substance.
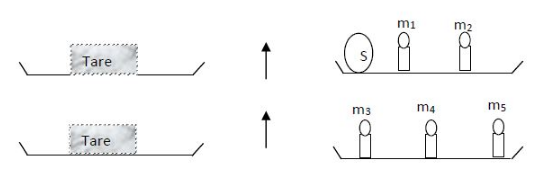
Exercice 21
Pour déterminer la masse d'un solide S on réalise les expériences suivantes à l'aide d'une balance Roberval

On donne :
$m_{1}=100\;g\;,\quad m_{2}=20\;g\;,\quad m_{3}=200\;g$
$m_{4}=10\;g\;,\quad m_{5}=2\;g$
1) On a réalisé une simple pesé
2) Déterminons la masse $m_{_{S}}$ du solide
Dans un premier temps, on a : $m_{_{S}}+m_{1}+m_{2}=\text{Tare}$
Et dans un second, on obtient : $m_{3}+m_{4}+m_{5}=\text{Tare}$
Ainsi, on a l'égalité : $m_{_{S}}+m_{1}+m_{2}=m_{3}+m_{4}+m_{5}$
Par suite,
$$m_{_{S}}=(m_{3}+m_{4}+m_{5})-(m_{1}+m_{2})$$
A.N : $m_{_{S}}=(200+10+2)-(100+20)=92$
Ainsi, $\boxed{m_{_{S}}=92\;g}$
3) En plongeant ce solide dans une éprouvette contenant un volume $V_{1}=55\;cm^{3}$ d'eau ; le niveau de l'eau remonte jusqu'à $215\;cm^{3}.$
Déterminons alors le volume $V_{_{S}}$ du solide
On sait que : $V_{_{S}}+V_{1}=215\;cm^{3}$
Donc, $V_{_{S}}=215\;cm^{3}-V_{1}$
A.N : $V_{_{S}}=215\;cm^{3}-55\;cm^{3}=160\;cm^{3}$
D'où, $\boxed{V_{_{S}}=160\;cm^{3}}$
4) Calculons la masse volumique $\rho_{_{S}}$ du solide
L'expression de la masse volumique est donnée par :
$$\rho_{_{S}}=\dfrac{m_{_{S}}}{V_{_{S}}}$$
alors, $\rho_{_{S}}=\dfrac{92}{160}=0.575$
Par suite, $\boxed{\rho_{_{S}}=0.575\;g.cm^{-3}=575\;g.l^{-1}}$
En déduisons sa densité $d_{_{S}}$ par rapport à l'eau
Sa densité par rapport à l'eau est donnée par :
$$d_{_{S}}=\dfrac{\rho_{_{S}}}{\rho_{e}}$$
avec, $\rho_{e}=1000\;g.l^{-1}$
A.N : $d_{_{S}}=\dfrac{575}{1000}=0.575$
Ainsi, $\boxed{d_{_{S}}=0.575}$
Exercice 24
Un bijou constitué d'un alliage d'or et de cuivre de masse $150\;g$ porte l'indication 18 carats.
1) Calculons la masse de l'or $m_{_{(\text{Or})}}$ et la masse de cuivre $m_{_{(\text{Cu})}}$ contenue dans ce bijou.
$-\ $ masse de l'or
On sait que l'indication 1 carat sur un alliage contenant de l'or signifie que $24\;g$ de cet alliage contient $1\;g$ d'or pur.
Donc, pour un bijou contenant de l'or et portant une indication 18 carats, on trouve $18\;g$ d'or pur dans $24\;g$ de ce bijou.
Par suite, on a la correspondance suivante :
$$\begin{array}{rcl} 24\;g_{_{(\text{alliage})}}&\longrightarrow&18\;g_{_{(\text{Or})}}\\150\;g_{_{(\text{alliage})}}&\longrightarrow&m_{_{(\text{Or})}}\end{array}$$
Ainsi, en utilisant la règle de proportionnalité, on obtient :
$\begin{array}{rcrcl}\dfrac{150}{24}=\dfrac{m_{_{(\text{Or})}}}{18}&\Rightarrow&m_{_{(\text{Or})}}\times 24&=&150\times 18\\ \\&\Rightarrow&m_{_{(\text{Or})}}&=&\dfrac{150\times 18}{24}\\ \\&\Rightarrow&m_{_{(\text{Or})}}&=&112.5\end{array}$
D'où, $\boxed{m_{_{(\text{Or})}}=112.5\;g}$
$-\ $ masse de cuivre
Le bijou étant un alliage d'or et de cuivre alors, on a :
$$m_{_{(\text{alliage})}}=m_{_{(\text{Or})}}+m_{_{(\text{Cu})}}$$
Ce qui donne : $m_{_{(\text{Cu})}}=m_{_{(\text{alliage})}}-m_{_{(\text{Or})}}$
A.N : $m_{_{(\text{Cu})}}=150-112.5=37.5$
Donc, $\boxed{m_{_{(\text{Cu})}}=37.5\;g}$
2) Calculons le volume de l'or $V_{_{(\text{Or})}}$ et celui du cuivre $V_{_{(\text{Cu})}}$ dans ce bijou.
$-\ $ volume de l'or
On a : $V_{_{(\text{Or})}}=\dfrac{m_{_{(\text{Or})}}}{\rho_{_{(\text{Or})}}}$
A.N : $V_{_{(\text{Or})}}=\dfrac{112.5}{19.3}=5.829$
D'où, $\boxed{V_{_{(\text{Or})}}=5.829\;cm^{3}}$
$-\ $ volume du cuivre
Soit : $V_{_{(\text{Cu})}}=\dfrac{m_{_{(\text{Cu})}}}{\rho_{_{(\text{Cu})}}}$
Alors, $V_{_{(\text{Cu})}}=\dfrac{37.5}{8.9}=4.213$
Donc, $\boxed{V_{_{(\text{Cu})}}=4.213\;cm^{3}}$
3) Calculons la masse volumique de l'alliage
On a : $\rho_{_{(\text{alliage})}}=\dfrac{m_{_{(\text{alliage})}}}{V_{_{(\text{alliage})}}}$
Or, $V_{_{(\text{alliage})}}=V_{_{(\text{Or})}}+V_{_{(\text{Cu})}}$ donc, on obtient :
$$\rho_{_{(\text{alliage})}}=\dfrac{m_{_{(\text{alliage})}}}{V_{_{(\text{Or})}}+V_{_{(\text{Cu})}}}$$
A.N : $\rho_{_{(\text{alliage})}}=\dfrac{150}{5.829+4.213}=\dfrac{150}{10.042}=14.937$
D'où, $\boxed{\rho_{_{(\text{alliage})}}=14.937\;g.cm^{-3}}$

Commentaires
Dama (non vérifié)
lun, 01/27/2020 - 15:36
Permalien
Correction de tout les exercices
Moustapha Fall (non vérifié)
jeu, 05/06/2021 - 09:42
Permalien
Exercice supplémentaire
Dessa (non vérifié)
jeu, 02/16/2023 - 21:36
Permalien
Repondre
Daniel. (non vérifié)
dim, 05/09/2021 - 22:30
Permalien
Merci
Dessa (non vérifié)
jeu, 02/16/2023 - 21:38
Permalien
répondre
Daniel. (non vérifié)
dim, 05/09/2021 - 22:30
Permalien
Merci
Khady (non vérifié)
mer, 06/02/2021 - 23:22
Permalien
Je trouve très intéressant
Djigo Aissata sidy (non vérifié)
lun, 03/20/2023 - 15:19
Permalien
De réussir mon projet
Djigo Aissata sidy (non vérifié)
lun, 03/20/2023 - 15:19
Permalien
De réussir mon projet
Djigo Aissata sidy (non vérifié)
lun, 03/20/2023 - 15:19
Permalien
De réussir mon projet
Faye (non vérifié)
ven, 04/26/2024 - 09:29
Permalien
Apprendre
Anonyme (non vérifié)
mar, 01/28/2020 - 22:35
Permalien
J'aime
Anonyme (non vérifié)
mar, 01/28/2020 - 23:09
Permalien
Tout les exercice
Ibrahima ly (non vérifié)
sam, 03/16/2024 - 17:02
Permalien
Sunu
Anonyme (non vérifié)
mer, 03/03/2021 - 22:27
Permalien
Sur la leçon portant sur la
Aladji (non vérifié)
mar, 01/28/2020 - 23:10
Permalien
Ba
Aladji (non vérifié)
mer, 01/29/2020 - 16:25
Permalien
Aba48932@gmail.comaladji
Youssou diallo (non vérifié)
mar, 02/25/2020 - 20:54
Permalien
Remerciement
Youssou diallo (non vérifié)
mar, 02/25/2020 - 20:54
Permalien
Remerciement
Diallo (non vérifié)
mer, 03/11/2020 - 15:38
Permalien
Demande
Diallo (non vérifié)
ven, 03/13/2020 - 22:46
Permalien
Demande
Anonyme (non vérifié)
sam, 03/14/2020 - 00:43
Permalien
Mais qu'est ce que vous
Sadio doucouré (non vérifié)
mer, 04/28/2021 - 19:27
Permalien
Sunudaara
Jihen maghrebi (non vérifié)
dim, 12/20/2020 - 07:46
Permalien
Remerciement
Anonyme (non vérifié)
jeu, 02/18/2021 - 05:31
Permalien
Très bon travail je vous
Ibwn (non vérifié)
mar, 03/30/2021 - 21:04
Permalien
Merci beaucoup pour les exos
Mens (non vérifié)
jeu, 04/22/2021 - 10:46
Permalien
Salut
Mens (non vérifié)
jeu, 04/22/2021 - 11:44
Permalien
Salut
Mens (non vérifié)
jeu, 04/22/2021 - 14:20
Permalien
Salut
Nana (non vérifié)
dim, 05/16/2021 - 14:48
Permalien
Merci
Sadio doucouré (non vérifié)
mer, 04/28/2021 - 19:29
Permalien
Sunudaara
Anonyme (non vérifié)
sam, 01/29/2022 - 19:13
Permalien
cool
Mabifa (non vérifié)
mar, 05/10/2022 - 23:07
Permalien
Encouragement
Mouhamad Saliou (non vérifié)
mer, 03/13/2024 - 21:40
Permalien
Remerciment
Ya awa (non vérifié)
mer, 03/20/2024 - 00:39
Permalien
Pc
Mohamed (non vérifié)
lun, 05/20/2024 - 22:22
Permalien
Une erreur
Antoine (non vérifié)
mer, 01/29/2025 - 15:57
Permalien
On a les mêmes objectifs
Je me nomme AWA... (non vérifié)
lun, 03/24/2025 - 19:52
Permalien
Je veux être capable de faire mais exercice moi même
Antoine (non vérifié)
mer, 01/29/2025 - 15:48
Permalien
exercice 23
Antoine (non vérifié)
mer, 01/29/2025 - 15:50
Permalien
exercice 23
jlullljj,;lluu (non vérifié)
sam, 01/17/2026 - 21:46
Permalien
lè;hljj,,h;j
jule cesard (non vérifié)
sam, 01/17/2026 - 21:47
Permalien
merci on est content
Mendy (non vérifié)
mer, 03/04/2026 - 00:49
Permalien
Apprendre
Ajouter un commentaire