Solution exercices : Propagation rectiligne de la lumière - 4e
Classe:
Quatrième
Exercice 1 Contrôle de connaissances
Recopions et complétons les phrases suivantes par les mots suivants : opaque, transparent, rectiligne, et translucide.
Dans un milieu transparent et homogène la lumière se propage de façon rectiligne.
Un milieu translucide laisse passer une partie de la lumière mais ne permet pas de distinguer les corps qui émettent cette lumière.
Un objet éclairé par une source placé derrière un écran transparent peut être distingué nettement. Un milieu opaque ne peut être traversé par la lumière.
Exercice 2
Recopions et complétons le tableau par "OUI" ou "NON"
$$\begin{array}{|l|l|l|l|} \hline \text{Corps}&\text{Transparent}&\text{Translucide}&\text{Opaque}\\ \hline \text{Eau}&\text{OUI}&\text{NON}&\text{NON}\\ \hline \text{Bois}&\text{NON}&\text{NON}&\text{OUI} \\ \hline \text{Papier huilé}&\text{NON}&\text{OUI}&\text{NON}\\ \hline \text{Vitre non teintée}&\text{OUI}&\text{NON}&\text{NON}\\ \hline\text{Huile}&\text{NON}&\text{OUI}&\text{NON}\\ \hline \text{Lait}&\text{NON}&\text{OUI}&\text{NON}\\ \hline \text{Paupière}&\text{NON}&\text{NON}&\text{OUI}\\ \hline \end{array}$$

Exercice 3
En 1850, Léon Foucault, astronome et physicien français du $19^{\text{ème}}$ siècle, démontre que la lumière se déplace moins vite dans l'eau puis, 12 ans plus tard, il évalue que la vitesse de la lumière dans l'air est d'environ de 300000 kilomètres par seconde avec une précision très satisfaisante.
1) Calculons le temps mis par la lumière pour parcourir un mètre dans l'air.
Soit $v$ la vitesse de la lumière dans l'air, $d$ la distance parcourue et $t$ le temps mis.
On a : $v=\dfrac{d}{t}$ ; ce qui veut dire que, $v\times t=d$
Par suite, $t=\dfrac{d}{v}\ $ avec $\ d=1\;m=10^{-3}\;km\ $ et $\ v=300000\;km.s^{-1}$
A.N : $t=\dfrac{10^{-3}}{300000}=3.333\;10^{-9}$
D'où, $\boxed{t=3.333\;10^{-9}\;s}$
2) Déterminons la distance parcourue par la lumière pendant une année dans l'air.
On a : $d=v\times t\ $ avec $\ t=1\;\text{année}$
Convertissons le temps $t$ en seconde.
On sait que : $1\;\text{année}=365\;\text{jours}\ $ et $\ 1\;\text{jour}=24\;h$
Donc, $1\;\text{année}=365\times 24\;h=8760\;h$ or, $1\;h=60\;mn\ $ et $\ 1\;mn=60\;s$
Par suite, $1\;\text{année}=8760\times 60\times 60=31536000\;s$
Ainsi, $d=300000\times 31536000=9460800000000$
D'où, $\boxed{d=9.4608\;10^{12}\;km}$
Cette longueur représente une année lumière.
3) Le soleil se trouve à environ $150000000\;km$ de la terre.
Calculons le temps que la lumière émise par le soleil met pour nous parvenir sur la terre.
Soit : $t=\dfrac{d}{v}\ $ avec $\ d=150000000\;km\ $ et $\ v=300000\;km.s^{-1}$
A.N : $t=\dfrac{150000000}{300000}=500$
Ainsi, $\boxed{t=500\;s=8\;mn\ 20\;s}$
Donc, la lumière émise par le soleil met $8\;mn\ 20\;s$ pour nous parvenir sur la terre.
Exercice 4
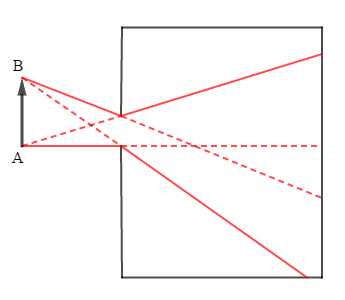
Un objet $AB$ est devant une chambre noire.
Reproduisons le schéma et traçons les rayons lumineux partant de $A\ $ et $\ B$ et pénétrant dans la chambre noire.

Les rayons plus clairs délimitent l'intervalle de propagation des rayons lumineux pénétrant dans la chambre.
Exercice 5
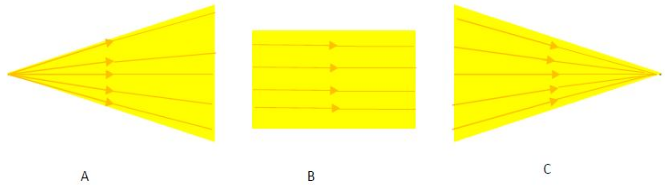
Considérons la figure ci-dessous

Les types de faisceaux lumineux observés sont :
$A\ $ : faisceaux divergents
$B\ $ : faisceaux parallèles
$C\ $ : faisceaux convergents
Exercice 6
Annotation

Signification des numéros indiqués :
$1-\ $ ombre propre
$2-\ $ cône d'ombre
$3-\ $ ombre portée

Signification des numéros indiqués :
$1-\ $ pénombre propre
$2-\ $ ombre propre
$3-\ $ pénombre portée
$4-\ $ ombre portée
Exercice 7
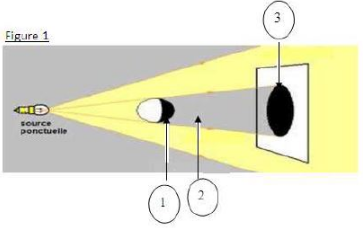
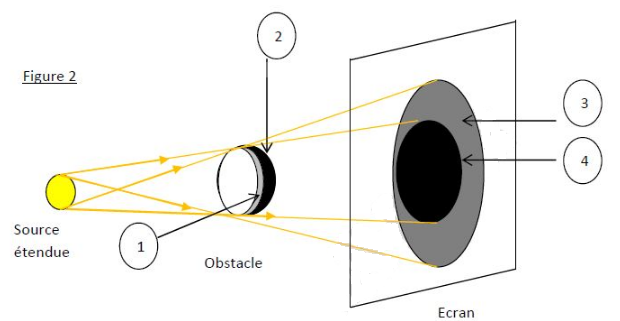
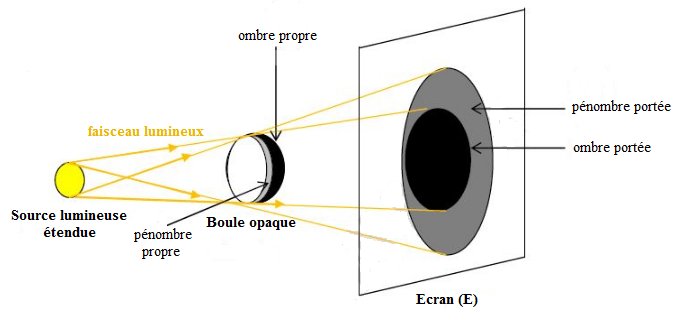
On éclaire un écran $E$ à l'aide d'une source lumineuse étendue puis une boule opaque est placée dans le faisceau lumineux.
Représentation de la source lumineuse étendue et du faisceau lumineux ainsi que l'ombre propre, la pénombre propre, l'ombre portée et la pénombre portée de la boule.

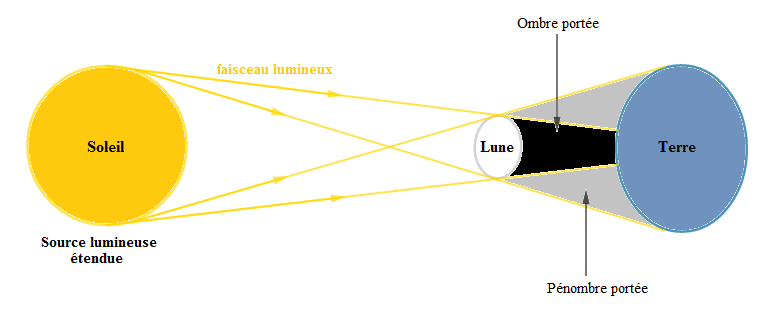
En nous inspirant du schéma précédent, expliquons, schéma à l'appui le phénomène de l'éclipse de Soleil.
On parle d'éclipse de soleil lorsque le soleil, la lune et la terre sont alignés dans cet ordre.

Cette position de la lune empêche totalement ou partiellement les faisceaux lumineux du soleil d'atteindre la surface de la terre.
$-\ $ Pour un observateur situé sur terre, à l'ombre portée de la lune, le soleil est totalement caché : on parle alors d'éclipse totale.
$-\ $ Un individu placé sur terre, à la pénombre portée de la lune, ne voit qu'une partie du soleil : on parle ainsi d'éclipse partielle.
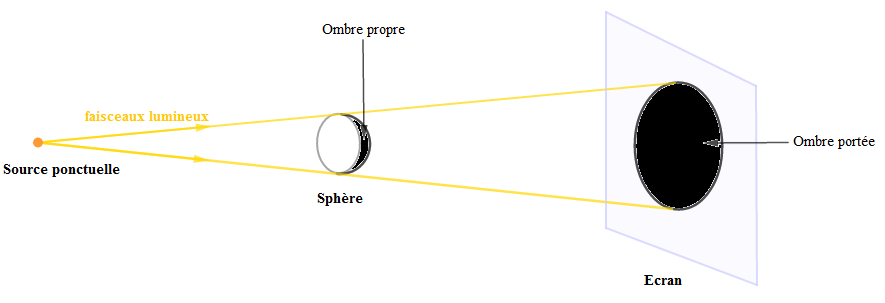
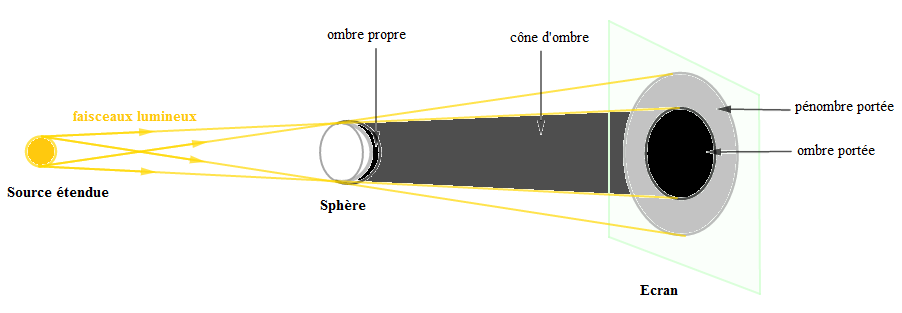
Exercice 8
1) Reproduisons la figure 1 et traçons les faisceaux lumineux, de la source ponctuelle jusqu'à l'écran, puis représentons l'ombre propre et l'ombre portée de la sphère.

2) Reproduisons la figure 2, puis représentons l'ombre propre de l'objet, son ombre portée, le cône d'ombre et la pénombre portée.

Exercice 9
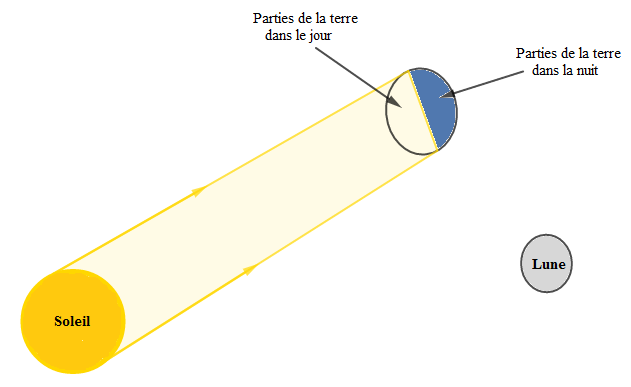
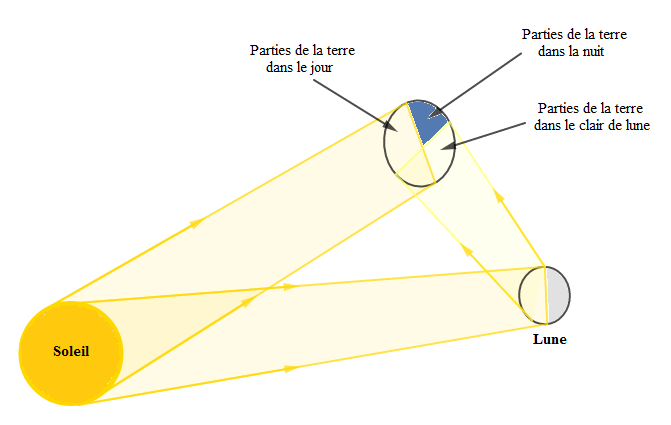
Dans le schéma ci-dessous sont représenté le Soleil, la Terre et la Lune
Le Soleil et la Lune sont deux sources de lumière.
1) Le soleil représente la source primaire et la lune la source secondaire.

2) Reproduisons en représentant les parties de la terre dans le jour et dans la nuit.

3) Reproduisons et représentons les parties de la terre dans le jour, dans la nuit et celles dans le clair de lune.


Commentaires
Anonyme (non vérifié)
mar, 03/24/2020 - 15:26
Permalien
Ny a pas la correction de l
Ramia (non vérifié)
sam, 05/02/2020 - 00:56
Permalien
...
MEZAROU Ghali (non vérifié)
mar, 04/27/2021 - 20:20
Permalien
Il n'y a pas la correction du dernier exercice
Anonyme (non vérifié)
sam, 05/15/2021 - 17:14
Permalien
fffffffffffffffffffffffffffff
Kouame (non vérifié)
ven, 10/16/2020 - 09:27
Permalien
Demande de mot de passe
Anonyme (non vérifié)
ven, 10/16/2020 - 09:29
Permalien
Par pdf adobe
Sylla (non vérifié)
lun, 12/28/2020 - 07:53
Permalien
La formation
ANASSÉ (non vérifié)
dim, 01/24/2021 - 15:40
Permalien
Professeur qui a à la recherche des exercices
ANASSÉ (non vérifié)
dim, 01/24/2021 - 15:44
Permalien
Professeur qui est à la recherche des exercices
Gisèle (non vérifié)
mar, 03/09/2021 - 04:53
Permalien
Merci pour vos efforts
Katche kouame (non vérifié)
dim, 10/10/2021 - 22:27
Permalien
Correction des exercices 8do
Fathi Borchani (non vérifié)
jeu, 05/04/2023 - 00:06
Permalien
Merci pour vos efforts
Ajouter un commentaire