Solutions des exercices : Mouvement d'une particule chargée dans un champ magnétique uniforme - Ts

 

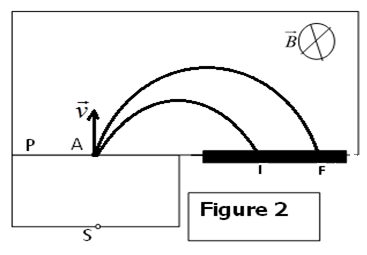
1) a) Détermination de l'expression littérale de la vitesse $v$ en $A$ d'un ion de masse $m$ et de charge $q$ en fonction de $m$, $e$ et $U$

 

Système étudié : l'ion 

 

Référentiel d'étude : terrestre

 

Bilan des forces appliquées : 

 

$-\ $la force électrique $\overrightarrow{F}$ 

 

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force électrique

 

Le théorème de l'énergie cinétique entre $S$ et $A$ s'écrit :

 

$$\begin{eqnarray} \Delta E_{C} &=&\sum\,W_{\overrightarrow{F}_{\text{EXT}}}\nonumber\\\\\Rightarrow E_{CA}-E_{CS} &=&W_{SA}\left(\overrightarrow{F}\right)\nonumber\\\\\Rightarrow\dfrac{1}{2}mv_{A}^{2}-0 &=&2eU\nonumber\\\\\Rightarrow v_{A} &=&\sqrt{\dfrac{2eU}{m}} \end{eqnarray}$$  

 

b) Montrons que les deux ions $_{80}^{200}Hg^{2+}$ et $_{80}^{202}Hg^{2+}$ émis par $S$ arrivent en $A$ avec des vitesses différentes.

 

Ayant la même charge et accélérés par le même champ, la vitesse des ions ne dépend que de leur masse. Ce qui explique bien la différence de vitesse des ions lorsqu'ils arrivent en $A.$

 

2) a) Établissement de l'expression de $R$ en fonction de $m$, $e$, $||\overrightarrow{B}||$ et $||\overrightarrow{V}||$ puis en fonction de $m$, $e$, $||\overrightarrow{B}||$ et $U.$

 

 

Système étudié : l'ion 

 

Référentiel d'étude : terrestre supposé galiléen

 

Bilan des forces appliquées : 

 

$-\ $la force magnétique $\overrightarrow{F}_{m}$  

 

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force magnétique

 

La deuxième de Newton s'écrit : 

 

$\overrightarrow{F}_{m}=m\vec{a}$

 

$\Rightarrow\,2e\vec{v}\wedge\overrightarrow{B}$

 

$\Rightarrow\,\vec{a}=\dfrac{2e\vec{v}\wedge\overrightarrow{B}}{m}$

 

$$\begin{eqnarray} \vec{v}\perp\overrightarrow{F_{_{m}}}\Rightarrow\vec{a}_{t} &=&\vec{0}\nonumber\\\\\Rightarrow\vec{a} &=&\overrightarrow{a}_{n}\nonumber\\\\\Rightarrow\,a_{n} &=&\dfrac{v^{2}}{R}\nonumber\\\\ &=&\dfrac{2evB}{m}\nonumber\\\\\Rightarrow R &=&\dfrac{mv}{2eB}\nonumber\\\\\text{or}\quad v &=&\sqrt{\dfrac{2eU}{m}}\nonumber\\\\\Rightarrow R &=&\dfrac{m\sqrt{\dfrac{2eU}{m}}}{2eB}\nonumber\\\\\Rightarrow R &=&\dfrac{1}{2B}\sqrt{\dfrac{2mU}{e}} \end{eqnarray}$$  

 

b) Calcul de $R_{1}$ et $R_{2}$

 

$$\begin{eqnarray} R_{1} &=&\dfrac{1}{2B}\sqrt{\dfrac{2m_{1}U}{e}}\nonumber\\\\ &=&\dfrac{1}{2\times 0.2}\sqrt{\dfrac{2\times 3.32\cdot 10^{-25}\times 600}{1.6\cdot 10^{-19}}}\nonumber\\\\\Rightarrow R_{1} &=&0.124\,m \end{eqnarray}$$  

 

$$\begin{eqnarray} R_{2} &=&\dfrac{1}{2B}\sqrt{\dfrac{2m_{2}U}{e}}\nonumber\\\\ &=&\dfrac{1}{2\times 0.2}\sqrt{\dfrac{2\times 3.35\cdot 10^{-25}\times 600}{1.6\cdot 10^{-19}}}\nonumber\\\\\Rightarrow R_{2} &=&0.125\,m \end{eqnarray}$$

 

La distance $IF$ entre les deux points d'impact

 

$$\begin{eqnarray} IF &=& 2\left(R_{2}-R_{1}\right)\nonumber\\\\ &=&2(0.125-0.124)\nonumber\\\\\Rightarrow IF &=&0.002\,m \end{eqnarray}$$

 

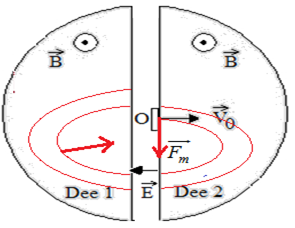
1.1. Expression de la force agissant sur le proton en $O$ 

 

$\overrightarrow{F}_{m}=q_{P}\overrightarrow{v_{0}}\wedge\overrightarrow{B}$ soit en module $F_{m}=q_{P}v_{0} B$

 

1.2. Montrons que la valeur de la vitesse est constante

 

$$\begin{eqnarray} \vec{v}\perp\overrightarrow{F_{m}}\Rightarrow\vec{a}_{t} &=&\vec{0}\nonumber\\\\\Rightarrow\,a_{t} &=&\dfrac{\mathrm{d}v}{\mathrm{d}\mathrm{t}}\nonumber\\\\ &=&0\nonumber\\\\\Rightarrow v &=&cte \end{eqnarray}$$  

 

1.3. Montrons que la trajectoire est circulaire de rayon $R_{0}=\dfrac{m_{P}}{q_{P}B}V_{0}$ 

 

$$\begin{eqnarray} \overrightarrow{a_{t}} &=& \vec{0}\nonumber\\\\\Rightarrow\overrightarrow{a} &=&\overrightarrow{a_{n}}\nonumber\\\\\Rightarrow\,a_{n} &=&\dfrac{v_{0}^{2}}{R_{0}}\nonumber\\\\ &=&\dfrac{q_{P}v_{0}B}{m}\nonumber\\\\\Rightarrow\,R_{0} &=&\dfrac{m_{P}v_{0}}{q_{P}B} \end{eqnarray}$$

 

Le rayon est constant, le mouvement est donc circulaire

 

2.1. Expression de la longueur parcourue par un proton sur le demi-tour de rayon $R_{0}$

$$l=\pi\,R_{0}=\dfrac{\pi m_{P}v_{0}}{q_{P}B}$$

 

2.2. Expression du temps t mis par ce proton pour effectuer ce demi-tour

 

$$\begin{eqnarray} t &=&\dfrac{l}{v_{0}}\nonumber\\\\ &=&\dfrac{\dfrac{\pi m_{P}v_{0}}{q_{P}B}}{v_{0}}\nonumber\\\\\Rightarrow\,t &=&\dfrac{\pi m_{P}}{q_{P}B} \end{eqnarray}$$

 

2.3. Ce temps est indépendant de la vitesse d'entrée du proton dans le «dee»

Calcul de la valeur de $t.$

 

$$\begin{eqnarray} \Rightarrow\,t &=&\dfrac{\pi m_{P}}{q_{P}B}\nonumber\\\\ &=&\dfrac{\pi\times 1.67\cdot 10^{-27}}{1.6\cdot 10^{-19}\times 1.0}\nonumber\\\\\Rightarrow t &=&3.3\cdot 10^{-8}s \end{eqnarray}$$

 

3. Calcul de la fréquence $f$

 

$$\begin{eqnarray} f &=&\dfrac{1}{2t}\nonumber\\\\ &=&\dfrac{1}{2\times 3.3\cdot 10^{-8}}\nonumber\\\\\Rightarrow f &=&15\cdot 10^{-8}s \end{eqnarray}$$

 

4.1. Expression littérale de la variation d'énergie cinétique $\Delta E_{c}$ du proton

 

Le théorème de l'énergie cinétique s'écrit :

 

$$\begin{eqnarray} \Delta E_{c} &=&\sum\,W_{\overrightarrow{F}_{\text{EXT}}}\nonumber\\\\\Rightarrow\Delta E_{c} &=& W_{SA}\left(\overrightarrow{F}\right)\nonumber\\\\ &=& q_{P}U_{M} \end{eqnarray}$$

 

Calcul de la variation d'énergie cinétique $\Delta E_{c}$ du proton

 

$$\begin{eqnarray}  \Delta E_{c} &=&q_{P}U_{M}\nonumber\\\\ &=& 1.6\cdot 10^{-19}\times 2\cdot 10^{3}\nonumber\\\\\Rightarrow\Delta E_{c} &=& 3.2\cdot 10^{-16}J \end{eqnarray}$$

 

$$\begin{eqnarray} \Delta E_{c} &=&\dfrac{q_{P}U_{M}}{e}\nonumber\\\\\Rightarrow\Delta E_{c} &=& 2\cdot 10^{3}eV \end{eqnarray}$$

 

$\left(e=q_{P}=1.6\cdot 10^{-19}C\right)$

 

4.2. Le rayon de la trajectoire du proton augmente à chaque fois qu'il traverse l'intervalle étroit puisque le rayon de la trajectoire augmente avec la vitesse. 

 

5. Calcul du nombre de tours que le proton décrits dans le cyclotron.

 

Le nombre de tours correspond à l'énergie finale de la particule divisée par l'énergie acquise à chaque tour.

 

$$\begin{eqnarray} n &=&\dfrac{\Delta E_{cf}}{2\Delta E_{c}}\nonumber\\\\ &=&\dfrac{\dfrac{1}{2}m_{P}v^{2}-0}{2\Delta E_{c}}\nonumber\\\\\Rightarrow n &=&\dfrac{1.67\cdot 10^{-27}\times\left(2\cdot 10^{7}\right)^{2}}{4\times 3.2\cdot 10^{-16}}\nonumber\\\\ &=& 552\text{tours} \end{eqnarray}$$

 

6. Calcul de la valeur du rayon 

 

$$\begin{eqnarray} R &=&\dfrac{m_{P}v}{q_{P}B}\nonumber\\\\ &=&\dfrac{1.67\cdot 10^{-27}\times 2\cdot 10^{7}}{1.6\cdot 10^{-19}\times 1.0}\nonumber\\\\\Rightarrow R &=&0.21\,m \end{eqnarray}$$

 

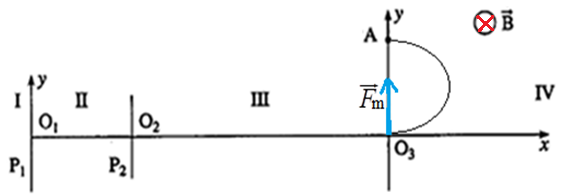
1) Expression de la force magnétique s'exerçant sur l'ion $X^{+}.$

 

$\overrightarrow{F_{m}}=e\vec{v}\wedge\overrightarrow{B}$ soit en module $F_{m}=evB$

 

Représentation sur un schéma du vecteur force $\overrightarrow{F_{m}}$ (Voir figure)

 

Sens du vecteur champ magnétique $\overrightarrow{B}$ (Voir figure)

 

2) Démontrons que le mouvement de l'ion $X^{+}$ dans la zone $IV$ est plan et uniforme

 

Système étudié : l'ion 

 

Référentiel d'étude : terrestre supposé galiléen

 

Bilan des forces appliquées : 

 

$-\ $la force magnétique $\overrightarrow{F_{m}}$ 

 

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force magnétique

 

Le théorème du centre d'inertie s'écrit :

 

$$\begin{eqnarray} \overrightarrow{F_{m}} &=&m\vec{a}\nonumber\\\\\Rightarrow e\vec{v}\wedge\overrightarrow{B}\nonumber\\\\ &=&m\vec{a}\nonumber\\\\\Rightarrow \vec{a} &=&\dfrac{e\vec{v}\wedge\overrightarrow{B}}{m} \end{eqnarray}$$

 

$\vec{a}\perp\overrightarrow{B}\ ;\ \vec{v}\perp\overrightarrow{B}\text{ et }\vec{a}\perp\overrightarrow{v}$ 

 

La trajectoire est contenue dans un plan orthogonal $\overrightarrow{B}.$ 

 

Le mouvement est donc plan.

 

$\vec{a}\perp\vec{v}\Rightarrow\overrightarrow{a_{t}}=\vec{0}$

 

$\Rightarrow\,a_{t}=\dfrac{\mathrm{d}v}{\mathrm{d}t}=0\Rightarrow\,v=cte$ 

 

Le mouvement est uniforme

 

3) Montrons que l'ion $X^{+}$ décrit dans cette zone un arc de cercle.

 

$$\begin{eqnarray} \overrightarrow{a_{t}} &=&\vec{0}\nonumber\\\\\Rightarrow\overrightarrow{a_{n}} &=&\overrightarrow{a}\nonumber\\\\\Rightarrow a_{n} &=&a\nonumber\\\\\Rightarrow\dfrac{v'^{2}}{R} &=&\dfrac{ev'B}{m}\nonumber\\\\\Rightarrow\,R &=&\dfrac{mv'}{eB}\nonumber\\\\ &=& cte \end{eqnarray}$$

 

L'ion $X^{+}$ décrit donc dans cette zone un arc de cercle

 

4) Expression le rayon du cercle trajectoire en fonction de $U'$, $m$, $e$ et $B.$

 

$$\begin{eqnarray} R &=&\dfrac{mv'}{eB}\nonumber\\\\\text{or }v' &=&\sqrt{\dfrac{2eU'}{m}}\nonumber\\\\\Rightarrow\,R &=&\dfrac{m\sqrt{\dfrac{2eU'}{m}}}{eB}\nonumber\\\\\Rightarrow\,R &=&\dfrac{1}{B}\sqrt{\dfrac{2mU'}{e}} \end{eqnarray}$$

 

5) Masse de l'ion $X^{+}$

 

$$\begin{eqnarray} O_{3}A &=&2R\nonumber\\\\ &=&\dfrac{2}{B}\sqrt{\dfrac{2mU'}{e}}\nonumber\\\\\Rightarrow\,O_{3}A^{2} &=&\dfrac{4}{B^{2}}\times\dfrac{2m U'}{e}\nonumber\\\\\Rightarrow m &=&\dfrac{eB^{2}O_{3}A^{2}}{8U'}\nonumber\\\\ &=&\dfrac{1.6\cdot 10^{-19}\times(1.80)^{2}\times(0.069)^{2}}{8\times 8.00\cdot 10^{3}}\nonumber\\\\\Rightarrow m &=&3.86\cdot 10^{-26}Kg \end{eqnarray}$$  

 

Identification de la substance $X.$

 

$$\begin{eqnarray} m &=& Am_{P}\nonumber\\\\\Rightarrow A &=&\dfrac{m}{m_{P}}\nonumber\\\\\Rightarrow A &=&\dfrac{3.86\cdot 10^{-26}}{1.67\cdot 10^{-27}}\nonumber\\\\ &=&23 \end{eqnarray}$$  

 

L'élément est le sodium de symbole $Na$  

 

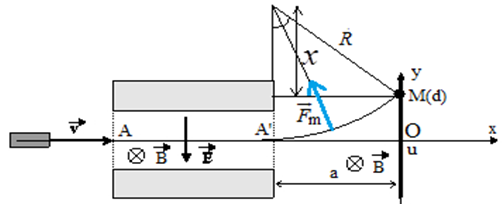
a) Valeur du champ électrique $\overrightarrow{E}$

 

Les particules ne sont pas déviées lorsque les deux forces électrique et magnétique auxquelles sont soumises se compensent.

 

$$\begin{eqnarray} \overrightarrow{F_{e}}+\overrightarrow{F_{m}} &=&\vec{0}\nonumber\\\\\Rightarrow q\overrightarrow{E}+q\vec{v}\wedge\overrightarrow{B} &=&\vec{0}\nonumber\\\\\Rightarrow\overrightarrow{E} &=&-\vec{v}\wedge\overrightarrow{B}\nonumber\\\\\Rightarrow\,E &=&vB\nonumber\\\\\Rightarrow\,v &=&\dfrac{E}{B}\nonumber\\\\ &=&\dfrac{6.4\cdot 10^{6}}{0.32}\nonumber\\\\\Rightarrow\,v &=&20.10^{6}m\cdot s^{-1} \end{eqnarray}$$

 

Il ne se passe rien si q change de signe puisque cette vitesse est indépendante de la charge.

 

b) i) Montons que les particules de même rapport $\dfrac{q}{m}$ décrivent des trajectoires circulaires de même rayon $R.$ 

 

$$\begin{eqnarray} \overrightarrow{F_{m}} &=&q\vec{v}\wedge\overrightarrow{B}\nonumber\\\\ &=&m\vec{a}\nonumber\\\\\Rightarrow|q|vB &=&ma_{n}\nonumber\\\\\Rightarrow|q|vB &=&m\dfrac{|v^{2}|}{R}\nonumber\\\\\Rightarrow\dfrac{|q|}{m} &=&\dfrac{v}{RB} \end{eqnarray}$$  

 

$v=cte\;,\ m=cte\ ;\ \text{si }\dfrac{|q|}{m}=cte\Rightarrow\,R=cte$

 

Les particules de même rapport $q/m$ décrivent des trajectoires circulaires de même rayon $R.$

 

Calcul de $R.$

 

Le signe $q$ détermine le sens de la déviation.

 

ii) Montrons que $R=\left(d^{2}+a^{2}\right)/2d.$

 

$$\begin{eqnarray} R^{2} &=&a^{2}+x^{2}\nonumber\\\\\text{ or }R &=&d+X\nonumber\\\\\Rightarrow X &=&R-d\nonumber\\\\\Rightarrow R^{2} &=&a^{2}+(R-d)^{2}\nonumber\\\\\Rightarrow R^{2} &=&a^{2}+R^{2}-2dR+d^{2}\nonumber\\\\\Rightarrow 2dR &=&a^{2}+d^{2}\nonumber\\\\\Rightarrow R &=&\dfrac{a^{2}+d^{2}}{2d} \end{eqnarray}$$  

 

Valeur de $q/m$

 

$$\begin{eqnarray} \dfrac{q}{m} &=&\dfrac{v}{RB}\nonumber\\\\ &=&\dfrac{2dv}{B\left(a^{2}+d^{2}\right)}\nonumber\\\\ &=&\dfrac{2\times 10\cdot 10^{-2}\times 20\cdot 10^{6}}{0.32\times\left(\left(5.0\cdot 10^{-2}\right)^{2}+\left(10\cdot 10^{-2}\right)^{2}\right)}\nonumber\\\\\Rightarrow\dfrac{q}{m} &=&48\cdot 10^{6}CKg^{-1} \end{eqnarray}$$

 

Identification des particules

 

$$\begin{eqnarray} \dfrac{q}{m} &=& 48\cdot 10^{6}CKg^{-1}\nonumber\\\\\Rightarrow m &=&\dfrac{q}{48\cdot 10^{6}}\nonumber\\\\\Rightarrow Am_{P} &=&\dfrac{q}{48\cdot 10^{6}}\nonumber\\\\ A &=&\dfrac{q}{48\cdot 10^{6}m_{P}}\nonumber\\\\ &=&\dfrac{q}{48\cdot 10^{6}\times 1830m_{e}}\nonumber\\\\ &=&\dfrac{1.6\cdot 10^{-19}}{48\cdot 10^{6}\times 1830\times 9.1\cdot 10^{-31}}\nonumber\\\\\Rightarrow A &=&2 \end{eqnarray}$$   

 

Les particules sont des deutériums 

 

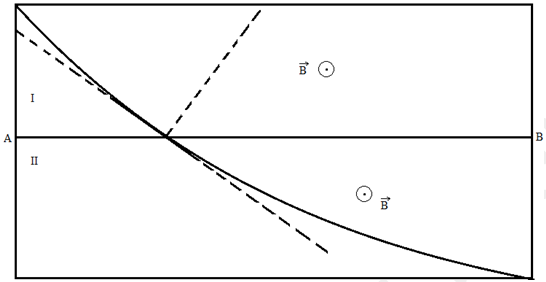
1) Établissement de l'expression de $r_{1}$ et $r_{2}$ en fonction de $q$, $m$, $B$ et des vitesses respectives $v_{1}$ et $v_{2}$ de la particule.

 

$$\begin{eqnarray} F_{m} &=&ma_{n}\nonumber\\\\ &=&\dfrac{mv^{2}}{r}\nonumber\\\\ &=&qvB\nonumber\\\\\Rightarrow\,r &=&\dfrac{mv}{qB}_nonumber\\\\\Rightarrow\,r_{1} &=&\dfrac{mv_{1}}{qB}\nonumber\\\\\text{et}\quad r_{2} &=&\dfrac{mv_{2}}{qB} \end{eqnarray}$$

 

$$\begin{eqnarray} \dfrac{r_{1}}{3} &=&r_{2}\nonumber\\\\\Rightarrow r_{2} &=&3r_{1}\nonumber\\\\\Rightarrow r_{2} &>& r_{1}\nonumber\\\\\Rightarrow\dfrac{mv_{2}}{qB} &>&\dfrac{mv_{1}}{qB}\nonumber\\\\\Rightarrow v_{2} &>& v_{1} \end{eqnarray}$$

 

Lorsque la particule ralentit, sa vitesse diminue. La particule se déplace de $II$ vers de $I$

Détermination de $v_{1}$ et $v_{2}.$

 

$v_{2}=2\cdot 10^{7}m\cdot s^{-1}$

 

$r=\dfrac{mv}{qB}\Rightarrow\dfrac{qB}{m}=\dfrac{v}{r}$

 

$$\begin{eqnarray} \dfrac{v_{1}}{r_{1}} &=&\dfrac{v_{2}}{r_{2}}\nonumber\\\\\Rightarrow v_{1} &=&\dfrac{r_{1}v_{2}}{r_{2}}\nonumber\\\\ &=&\dfrac{1}{3}\times 2\cdot 10^{7}\nonumber\\\\\Rightarrow v_{1} &=& 6.7\cdot 10^{6}m\cdot s^{-1} \end{eqnarray}$$  

 

2) Le signe de la particule est positif. Le trièdre doit être direct et la particule se déplace   de $II$ vers de $I$

 

3) Calcul de la charge massique $\dfrac{q}{m}$

 

$$\begin{eqnarray} \dfrac{q}{m} &=&\dfrac{v}{r_{2}B}\nonumber\\\\ &=&\dfrac{2.0\cdot 10^{7}}{3\times 14\cdot 10^{-2}\times 0.50}\nonumber\\\\\Rightarrow\dfrac{q}{m} &=&9.5\cdot 10^{7}CKg^{-1} \end{eqnarray}$$

 

Identification de la particule

 

$$\begin{eqnarray} \dfrac{q}{m} &=&9.5\cdot 10^{7}CKg^{-1}\nonumber\\\\\Rightarrow q &=&9.5\cdot 10^{7}m\nonumber\\\\\Rightarrow Ze &=&9.5\cdot 10^{7}m\nonumber\\\\\Rightarrow Z &=&\dfrac{9.5\cdot 10^{7}m}{e}\nonumber\\\\ &=&\dfrac{9.5\cdot 10^{7}\times 1.67\cdot 10^{-27}}{1.6\cdot 10^{-19}} \end{eqnarray}$$  

 

$Z=1$ La particule est un proton 

 

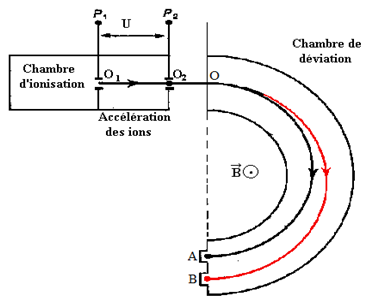
1) a) La tension doit être établie de façon que la plaque $P_{2}$ soit chargée négativement.

 

b) Montrons que l'énergie cinétique, est indépendante de l'isotope envisagé.

 

Système étudié : l'ion 

 

Référentiel d'étude : terrestre

 

Bilan des forces appliquées : 

 

$-\ $la force électrique $\overrightarrow{F}$

  

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force électrique

 

Le théorème de l'énergie cinétique entre $P_{1}$ et $P_{2}$ s'écrit :

 

$$\begin{eqnarray} \Delta E_{c} &=& W\left(\overrightarrow{F}\right)\nonumber\\\\ &=&2eU\nonumber\\\\\Rightarrow E_{C_{p_{2}}}-0 &=&2eU\nonumber\\\\\Rightarrow E_{C_{p_{2}}} &=&2eU  \end{eqnarray}$$

 

L'énergie cinétique, ne dépend que de la tension accélératrice

 

$$\begin{eqnarray} E_{C_{p_{2}}} &=& 2eU\nonumber\\\\ &=&2\times 1.6\cdot 10^{-19}\times 1000\nonumber\\\\\Rightarrow\,E_{C_{p_{2}}} &=&3.2\cdot 10^{-16}J \end{eqnarray}$$

 

c) Calcul de la vitesse acquise par les ions $_{54}^{129}Xe^{+}$

 

$$\begin{eqnarray} \dfrac{1}{2}mv^{2} &=& E_{C_{p_{2}}}\nonumber\\\\\Rightarrow\,v &=&\sqrt{\dfrac{2E_{C_{p_{2}}}}{129m_{P}}}\nonumber\\\\ &=&\sqrt{\dfrac{2\times 3.2\cdot 10^{-16}}{129\times 1.67\cdot 10^{-27}}}\nonumber\\\\\Rightarrow\,v &=&5.45\cdot 10^{4}m\cdot s^{-1} \end{eqnarray}$$  

 

d) Expression, en fonction de $x$ et $v$, de la vitesse $v'$ acquise par les ions $_{54}^{x}Xe^{+}$ en $O_{2}$

 

$\dfrac{1}{2}\times 129m_{P}v^{2}=2eU$ ;

 

$$\begin{eqnarray} \dfrac{1}{2}xm_{P}v'^{2} &=& 2eU\nonumber\\\\\Rightarrow\dfrac{1}{2}xm_{P}v'^{2} &=&\dfrac{1}{2}\times 129m_{P}v^{2}\nonumber\\\\\Rightarrow\,v' &=&v\sqrt{\dfrac{129}{x}} \end{eqnarray}$$

 

2) Séparation des ions

 

a) Montrons que le mouvement est plan, circulaire et uniforme

 

Système étudié : l'ion

 

Référentiel d'étude : terrestre supposé galiléen

 

Bilan des forces appliquées : 

 

$-\ $la force magnétique $\overrightarrow{F_{m}}$

 

$-\ $le poids négligeable $\overrightarrow{P}$ devant la force magnétique

 

Le théorème de centre d'inertie s'écrit :

 

$$\begin{eqnarray} \overrightarrow{F_{m}} &=&m\vec{a}\nonumber\\\\\Rightarrow\,e\vec{v}\wedge\overrightarrow{B} &=&m\vec{a}\nonumber\\\\\Rightarrow\vec{a} &=&\dfrac{e\vec{v}\wedge\overrightarrow{B}}{m} \end{eqnarray}$$

 

$\vec{a}\perp\overrightarrow{B}\ ;\ \vec{v}\perp\overrightarrow{B}\quad\text{et}\quad\vec{a}\perp\vec{v}$ 

 

La trajectoire est contenue dans un plan orthogonal $\overrightarrow{B}$  

 

Le mouvement est donc plan

 

$$\begin{eqnarray} \vec{a}\perp\vec{v}\Rightarrow\vec{a_{t}} &=&\vec{0}\nonumber\\\\\Rightarrow\,a_{t} &=&\dfrac{\mathrm{d}v}{\mathrm{d}t}\nonumber\\\\ &=&0\nonumber\\\\\Rightarrow\,v &=&cte \end{eqnarray}$$

 

Le mouvement est uniforme

 

$$\begin{eqnarray} \vec{a_{t}} &=&\vec{0}\nonumber\\\\\Rightarrow\,\vec{a_{n}} &=&\vec{a}\nonumber\\\\\Rightarrow\,a_{n} &=& a\nonumber\\\\\Rightarrow\dfrac{v^{2}}{R} &=&\dfrac{evB}{m}\nonumber\\\\\Rightarrow\,R &=&\dfrac{mv}{eB}\nonumber\\\\ &=&cte \end{eqnarray}$$

 

Le mouvement est circulaire

 

Expression du rayon de courbure $R.$ 

 

$$\begin{eqnarray} R &=&\dfrac{mv}{eB}\nonumber\\\\ &=&\dfrac{129\times 1.67\cdot 10^{-27}\times 5.45\cdot 10^{4}}{1.6\cdot 10^{-19}\times 0.1}\nonumber\\\\\Rightarrow\,R &=&0.734m \end{eqnarray}$$

 

b) Valeur de $x$

 

$$\begin{eqnarray} AB &=&2R'-2R\nonumber\\\\ &=&2\left(\dfrac{xm_{P}v'}{eB}-\dfrac{129m_{P}v}{eB}\right)\nonumber\\\\ &=& 2\left(\dfrac{xm_{P}}{eB}v\sqrt{\dfrac{129}{x}}-\dfrac{129m_{P}v}{eB}\right)\nonumber\\\\ &=&2\left(\dfrac{m_{P}}{eB}v\sqrt{129x}-\dfrac{129m_{P}v}{eB}\right)\nonumber\\\\\Rightarrow\dfrac{m_{P}}{eB}v\sqrt{129x} &=&\dfrac{AB}{2}+\dfrac{129m_{P}v}{eB}\nonumber\\\\\Rightarrow\sqrt{129x} &=&\dfrac{eB\cdot AB}{2m_{P}v}+129\nonumber\\\\\Rightarrow\,x &=&\dfrac{1}{129}\left(\dfrac{eB\cdot AB}{2m_{P}v}+129\right)^{2}\nonumber\\\\ &=&\dfrac{1}{129}\left(\dfrac{1.6\cdot 10^{-19}\times 0.1\times 8\cdot 10^{-2}}{2\times 1.67\cdot 10^{-27}\times 5.45\cdot 10^{4}}+129\right)^{2}\nonumber\\\\\Rightarrow\,x &=&143 \end{eqnarray}$$