Vous êtes ici

Travail et puissance mécaniques - 1er s

Classe:

Première

I. Travail d'une force

1. Observations

Un ouvrier monte un sac à l'aide d'une poulie. Lorsque le sac monte, l'ouvrier travail. Lorsque le reste immobile l'ouvrier se fatigue mais ne travaille pas.

Une pierre tombe verticalement sous l'action de la pesanteur. Le poids de la pierre est une force qui se déplace, il effectue un travail.

2. Définition

Une force travail lorsque son poids d'application se déplace

3. Expression du travail d'une force

3.1. Expression du travail d'une force constante

Une force constante est représentée par un vecteur qui reste parallèle à lui-même et qui conserve le même sens, et la même valeur (intensité) au cours du temps.

3.1.1. Expression du travail d'une force constante sur un déplacement rectiligne

Dans un référentiel donné, le travail

$(w)$ d'une force constante

$(F)$ dont le point d'application de

$A$ à

$B$ se déplace suivant une ligne droite est donné par :

$W_{AB}\left(\overrightarrow{F}\right)=\overrightarrow{F}\cdot\overrightarrow{AB}=||\overrightarrow{F}||||\overrightarrow{AB}||\cos(\overrightarrow{F}\overrightarrow{AB})$

On pose :

$||\overrightarrow{F}||=F$ et

$||\overrightarrow{AB}||=AB$

$\Rightarrow W_{AB}\left(\overrightarrow{F}\right)=F\cdot AB=F\ AB\cos\alpha$

$\overrightarrow{F}$ en newtons

$(N)$ ;

$AB$ en mètres

$(m)$ ;

$W_{AB}(\overrightarrow{F})$ en joules

$(J)$

$\blacktriangleright\$ Travail moteur et resistant

Les deux valeurs

$F$ et

$AB$ étant toujours positives, le signe du travail dépend de l'angle.

Le travail est donc une grandeur algébrique c'est-à-dire, il peut être positif ou négatif.

3.1.2. Expression du travail d'une force constante sur un déplacement quelconque

La trajectoire

$AB$ peut être découpée en une infinité de petits vecteurs déplacent élémentaires rectilignes

$\overrightarrow{AB}=\overrightarrow{AA_{1}}+\overrightarrow{A_{1}A_{2}}+\ldots\overrightarrow{A_{n}B}$

Le travail total est la somme de des travaux élémentaires successifs

$W_{AB}(\overrightarrow{F})=\overrightarrow{F}\cdot\overrightarrow{AA_{1}}+\overrightarrow{F}\cdot\overrightarrow{A_{1}A_{2}}+\ldots\overrightarrow{F}\cdot\overrightarrow{A_{n}B}$

$\Rightarrow W_{AB}(\overrightarrow{F})=\overrightarrow{F}\cdot\left(\overrightarrow{AA_{1}}+\overrightarrow{A_{1}A_{2}}+\ldots\overrightarrow{A_{n}B}\right)$

$\Rightarrow W_{AB}(\overrightarrow{F})=\overrightarrow{F}\cdot\overrightarrow{AB}$

$\Rightarrow W_{AB}(\overrightarrow{F})=F\cdot AB=F\ AB\cos\alpha$

Le travail d'une force constante

$F$ ne dépend pas du chemin suivi. Il ne dépend que du point de départ et du point d'arrivée. La force

$F$ est appelée « Force conservative ».

$\blacktriangleright\$ Application au travail du poids

Calculons le travail du poids au cours de son déplacement entre

$A$ et

$B$ :

Le travail s'écrit :

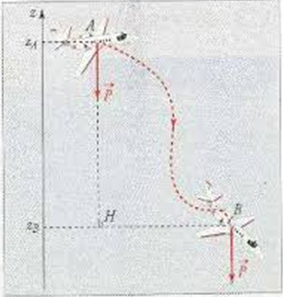
$\begin{eqnarray} W_{AB}\left(\overrightarrow{P}\right) &=&\overrightarrow{P}\cdot\overrightarrow{AB}\nonumber \\ &=&\overrightarrow{P}\cdot\left(\overrightarrow{AH}+\overrightarrow{HB}\right)\nonumber\\ &=&\overrightarrow{P}\cdot\overrightarrow{AH}+\overrightarrow{P}\cdot\overrightarrow{HB} \end{eqnarray}$

Or l'angle entre

$\overrightarrow{P}$ et

$\overrightarrow{HB}$ est un angle de

$90^{\circ}$ donc le produit scalaire de ces deux grandeurs sera nul.

Soit

$W_{AB}\left(\overrightarrow{P}\right)=\overrightarrow{P}\cdot\overrightarrow{AH}$

De plus

$AH=z_{A}-z_{B}$ et

$P=mg$

Finalement

$W_{AB}\left(\overrightarrow{P}\right)=mg(z_{A}-z_{B})$

Lorsque le centre d'inertie

$G$ d'un corps passe d'un point

$A$ à un point

$B$ , le travail du poids dépend seulement de l'altitude

$z_{A}$ du point de départ et de l'altitude

$z_{B}$ du point d'arrivée. Il ne dépend donc pas du chemin suivi.

Remarque :

On définit une différence d'altitude

$h=\left|z_{A}-z_{B}\right|$ ; on a alors :

$W_{AB}\left(\overrightarrow{P}\right)=\pm mgh$

$\blacktriangleright\$ Le signe plus

$(-)$ signifie que le corps descend (travail moteur)

$\blacktriangleright\$ Le signe plus

$(+)$ signifie que le corps monte (travail résistant)

3.2. Expression du travail d'une force de moment constant

3.2.1. Expression du travail du couple de force

$F_{1}=F_{1}=F$

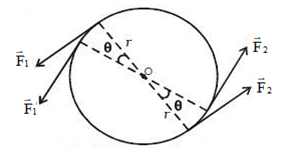
$\begin{eqnarray} W &=& W\left(\overrightarrow{F}_{1}\right)+W\left(\overrightarrow{F}_{2}\right)\nonumber \\\\ &=& F_{1}r\theta+F_{2}r\theta\nonumber \\\\ &=& F\left(r\theta+r\theta\right) \nonumber\\\\ &=& F\times 2r\theta \nonumber \\\\\Rightarrow W &=&M_{c}\theta \end{eqnarray}$

$M_{c}$ en newtons mètres

$(Nm)$ ; en radians

$(rad)$ ;

$W$ en joules

$(J)$

3.2.2. Généralisation

Le travail

$W$ effectuée par un force de moment constant, agissant sur un solide tournant d'un angle

$\theta$ autour d'un axe fixe est donné par la relation :

$W=M_{c}\theta$

$\theta$ est positif si la relation s'effectue sur le sens positif

$\theta$ est négatif si la relation s'effectue sur le sens négatif

3.3. Expression du travail d'une force variable

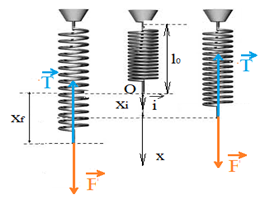
3.3.1. Expression du travail d'une force élastique

Le travail de la force élastique du ressort de raideur

$K$ dont l'allongement passe progressivement de

$x_{i}$ à

$x_{f}$ est donné par l'expression :

$W_{\overrightarrow{T}}=-\dfrac{1}{2}K\left(X_{f}^{2}-X_{i}^{2}\right)$

$K$ en

$N\cdot m^{-1}$ ;

$x_{i}$ et

$x_{f}$ en

$m$ et

$W_{\overrightarrow{T}}$ en

$J$

Le travail de la tension est un travail résistant

La tension est une force conservatrice

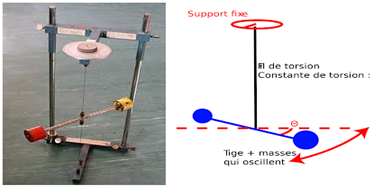
3.3.2. Expression du travail des forces de torsion

Le travail

$W$ des forces de torsion d'un fil de constante de torsion

$(C)$ tordu progressivement de

$\theta_{i}$ à

$\theta_{f}$ est donné par l'expression :

$W_{c}=-\dfrac{1}{2}K\left(\theta_{f}^{2}-\theta_{i}^{2}\right)$

$C$ constante de torsion en

$N\cdot m\cdot rad^{-1}$ ;

$\theta_{i}$ et

$\theta_{f}$ en

$rad$ et

$W_{c}$ en

$J$

II. Puissance

1. Observation

Pour soulever une charge

$(s)$ d'une hauteur

$(h)$ , une grue est plus efficace que l'homme (La grue met moins de temps que l'homme). Pourtant, le travail effectué par la grue est la même que celui effectué par l'homme.

On dit que la puissance de la grue est grande à celle de l'homme.

2. Définition

La puissance mécanique d'une force caractérise sa capacité à effectuer sur travail donné rapidement.

3. La puissance moyenne

La puissance moyenne d'une force est le quotient du travail effectué par la force et par le temps mis pour l'effectuer.

$P_{\text{Moyenne}}=\dfrac{W}{\Delta t}$

$W$ en joules

$(J)$ ;

$\Delta t$ en secondes

$(s)$ et

$P_{\text{Moyenne}}$ en watts

$(W)$ ;

4. Puissance instantanée d'une force

4.1. Puissance instantanée d'une force en mouvement de translation

La puissance instantanée d'une force en mouvement de translation est donnée par la relation :

$\begin{eqnarray} P&=&\dfrac{W_{\overrightarrow{F}}}{t}\nonumber\\\\ &=&\dfrac{\overrightarrow{F}\cdot\overrightarrow{AB}}{t}\nonumber\\\\ &=&\overrightarrow{F}\cdot\overrightarrow{v}\nonumber\\\\\Rightarrow\;P &=& Fv\cos\left(\overrightarrow{F}\;,\ \overrightarrow{v}\right)\end{eqnarray}$

4.2. Puissance instantanée d'une force quelconque appliquée à un solide en rotation

La puissance instantanée d'une force quelconque s'exerçant sur un solide tournant autour d'un axe fixe est à chaque instant :

$\begin{eqnarray} P&=&\dfrac{W}{t}\nonumber\\\\ &=&\dfrac{M_{\Delta}\left(\overrightarrow{F}\right)\times\theta}{t}\nonumber\\\\ &=&M_{\Delta}\left(\overrightarrow{F}\right)\times\dfrac{\theta}{t}\nonumber\\\\\Rightarrow\;P &=&M_{\Delta}\left(\overrightarrow{F}\right)\omega\end{eqnarray}$

Avec

$M_{\Delta}\left(\overrightarrow{F}\right)$ en

$N\cdot m$ en

$\omega$ en

$rads^{-1}$ et

$P$ en

$W$

Remarque :

Autre unité du travail : le kilowattheure

$W=P\times t$

$P$ est

$kW$ et

$t$ en

$h$ alors

$W$ sera donc en kilowattheure

$1kWh=1kW\times 1h=10^{3}\times 3600\Rightarrow\;1kWh=36\cdot10^{5}$

Autre unité de puissance : le cheval vapeur

$(Ch)$

$1Ch=736W$

Quelques valeurs de puissance

$\begin{array}{|l|c|} \hline \text{Formule 1}&600kW\\ \hline \text{Centrale hydraulique}&400MW\\ \hline \text{Moteur de TGV}&6400kW\\ \hline \text{Réacteur de centrale nucléaire}&900MW\\ \hline \end{array}$

Exercice d'application

Le point d'application d'une force est déplacé dans un repère orthonormé

$\left(O\;,\ \vec{i}\;,\ \vec{j}\right)$

On donne :

$\overrightarrow{F}=\sigma\vec{i}$

$G$ est déplacé successivement de

$A$ à

$B$ puis de

$B$ à

$C$ en fin de

$C$ à

$D.$ on donne :

$\overrightarrow{OA}=2\vec{i}+4\vec{j}$ ;

$\overrightarrow{OB}=-3\vec{i}+4\vec{j}$ ;

$\overrightarrow{OC}=2\vec{i}+8\vec{j}$

$\overrightarrow{OD}=-4\vec{j}$

Les coordonnées sont en

$cm$

Calculer le travail effectué par la force sur chaque déplacement

Résolution :

Calcul du travail effectué par la force sur chaque déplacement :

$\blacktriangleright\$ Sur le déplacement

$AB$

$\begin{eqnarray} W_{AB}\left(\overrightarrow{F}\right)&=&\overrightarrow{F}\cdot\overrightarrow{AB} \nonumber\\\\ &=& \overrightarrow{F}\cdot\left(\overrightarrow{AO}+\overrightarrow{OB}\right) \nonumber\\\\ &=&6\vec{j}\cdot\left(-2\vec{i}-4\vec{j}+-3\vec{i}+4\vec{j}\right)\nonumber\\\\&=&6\vec{j}\cdot-5\vec{i}\nonumber\\\\ &=&6\times-5\cdot10^{-2}\nonumber\\\\ \Rightarrow\;W_{AB}\left(\overrightarrow{F}\right) &=& -30\cdot10^{-2}J\end{eqnarray}$

$\blacktriangleright\$ Sur le déplacement

$BC$

$\begin{eqnarray} W_{BC}\left(\overrightarrow{F}\right)&=&\overrightarrow{F}\cdot\overrightarrow{BC} \nonumber\\\\ &=& \overrightarrow{F}\cdot\left(\overrightarrow{BO}+\overrightarrow{OC}\right) \nonumber\\\\ &=&6\vec{j}\cdot\left(3\vec{i}-4\vec{j}+2\vec{i}+8\vec{j}\right)\nonumber\\\\&=&6\vec{j}\cdot4\vec{j}\nonumber\\\\ &=&6\times4\cdot10^{-2}\nonumber\\\\ \Rightarrow\;W_{BC}\left(\overrightarrow{F}\right) &=& 24\cdot10^{-2}J\end{eqnarray}$

$\blacktriangleright\$ Sur le déplacement

$CD$

$\begin{eqnarray} W_{CD}\left(\overrightarrow{F}\right)&=&\overrightarrow{F}\cdot\overrightarrow{CD} \nonumber\\\\ &=& \overrightarrow{F}\cdot\left(\overrightarrow{CO}+\overrightarrow{OD}\right) \nonumber\\\\ &=&6\vec{j}\cdot\left(-2\vec{i}-8\vec{j}-4\vec{j}\right)\nonumber\\\\&=&6\vec{j}\cdot-12\vec{j}\nonumber\\\\ &=&6\times-12\cdot10^{-2}\nonumber\\\\ \Rightarrow\;W_{CD}\left(\overrightarrow{F}\right) &=& -72\cdot10^{-2}J\end{eqnarray}$

Auteur:

Sidy Mouhamed Ndiaye

Commentaires

Cheikhdieng002 (non vérifié)

dim, 07/25/2021 - 14:08

Permalien

Ff

tggedd

répondre

Laplace (non vérifié)

sam, 09/18/2021 - 11:31

Permalien

Cours

Bon cours

répondre

Anonyme (non vérifié)

dim, 11/14/2021 - 01:56

Permalien

Nice

répondre

Anonyme (non vérifié)

dim, 11/14/2021 - 01:57

Permalien

Nice

répondre

Dame Drame (non vérifié)

dim, 11/21/2021 - 09:02

Permalien

Document pdf

C'est un cours très bien fait.Merci

répondre

Sidymohamed.ndi... (non vérifié)

mer, 05/18/2022 - 23:51

Permalien

Merci pour les compliments

Merci pour les compliments et je suis à l'écoute s'il y a des choses qui ne sont pas claires ou s'il y a des choses à améliorer . Un cours n est jamais parfait

répondre

Abou Deme (non vérifié)

lun, 11/14/2022 - 21:47

Permalien

Le W est négatif le travail

Le W est négatif le travail est résistant le corps montre Le W positif le travail est moteur donc l corps descend . Merci.

répondre

ZADI (non vérifié)

dim, 10/09/2022 - 05:20

Permalien

Demande du PDF

Merci monsieur pour votre altruisme. Cependant sans abuser de votre générosité est-il possible de l'avoir en format pdf ? Si oui laissez moi le lien en commentaire svp.