Quatrième partie : Hérédité : Lois statistiques de la transformation des caractères héréditaire - Ts s
Classe:
Terminale
Thème:
8 Héridité-génétique
Introduction
La reproduction sexuée est une fonction biologique permettant aux êtres vivants de donner des descendances qui leurs ressemblent morphologiquement et ou physiologiquement au cours des générations.
Cette transmission de caractères d'une génération à une autre est appelée hérédité.
La science qui s'occupe de l'étude de l'hérédité est la génétique.
La compréhension des résultats de la génétique repose sur l'étude des lois statistiques.
I. Quelques notions fondamentales de génétiques
∙ Les caractères sont des signes distinctifs, des états ou des marques particulières d'un organisme.
Exemple :
La couleur (du pelage, des yeux, des fruits, des graines, des fleurs, etc...) ; la forme (ronde, ovale), la taille (longue ou courte...) ; la présence ou l'absence d'un élément (corne, queue, mélanine...) ; l'aspect (lisse, rugueux, lobé)
∙ On appelle population l'ensemble des individus d'une même espèce, vivant dans le même milieu.
∙ La génétique utilise une méthode expérimentale essentiellement basée sur des croisements, c'est-à-dire que l'on fait reproduire des individus appartenant à la même espèce pour pouvoir suivre le ou les caractères à étudier.
∙ Si dans une population possédant un caractère donné, les croisements entre les différents individus donnent toujours le même caractère, on en déduit que ce caractère étudié est pure.
Une lignée pure pour un (ou des) caractère(s) est un ensemble d'individus n'ayant et ne transmettant que ce (ou ces) caractère(s).
∙ Une lignée hybride pour un (ou des) caractère(s) est un ensemble d'individus qui, par croisement, donne une descendance hétérogène pour ce caractère.
∙ Le phénotype est l'ensemble des caractères visibles d'un individu.
Exemple :
La couleur, du pelage : [grise] ou [blanche] ; la forme des graines [ronde] etc...
∙ Le génotype est l'ensemble des facteurs héréditaires responsables de l'apparition des caractères qui déterminent le phénotype.
Chaque caractère est représenté par deux facteurs constituant un gène.
Chacun de ces facteurs est un allèle.
− Si les deux (2) allèles d'un gène sont identiques, l'individu qui les porte est de lignée pure et on dit qu'il est homozygote.
− Si les deux (2) allèles d'un gène sont différents, l'individu qui les porte est Hybride et on dit qu'il est hétérozygote.
− Le génome est l'ensemble de tous les gènes d'un individu.
II. Descendance de parents différents par un seul caractère : le mono hybridisme
II.1. Mono hybridisme avec dominance
√ Croisement de deux races pures
On dispose d'une souris de lignée pure dont le pelage est gris.
On effectue un croisement de cette lignée pure de souris avec une autre lignée pure composée de souris blanches.
On obtient à la descendance des individus de la première génération notée F1.
Au niveau de cette génération F1, on remarque que toutes les souris sont grises.
Parents : souris blanches x souris grises
⇓
Première génération F1 : souris grises
− Résultats numériques : toutes les souris sont grises (exemple : 10 souris grises)
− Résultats statistiques : on obtient 100% de souris grises.
Analyse :
On constate qu'en F1, la couleur blanche n'apparait pas
Hypothèse :
Le caractère blanc serait absent ou serait masqué au niveau des individus de la F1
Vérifions cette hypothèse avec un croisement F1 x F1
√ Croisement des individus F1 entre eux
On croise les individus de la F1 entre eux c'est-à-dire, on prend un mâle gris de la F1 que l'on croise avec une de ses sœurs (de la F1).
On obtient des individus de deuxième génération notée F2.
− Résultats numériques de la F2 : 39 souris grises et 14 souris blanches
− Résultats statistiques : Cherchons les rapports :
39+14=53
53/14=3.78 (environ égal à 4) ;
39/14=2.78 (environ égal à 3) ;
14/14=1
Donc la F2 est composée de 1/4 (ou 25%) de souris blanches +3/4 (ou 75%) de souris grises
Analyse :
On constate que la couleur blanche réapparait en F2
Interprétation :
Si la F2 a donné le caractère blanc, c'est parce que ce dernier existait en F1 mais qu'il était masqué par le caractère gris.
Le caractère gris est dit dominant et est noté G ; le caractère blanc est dit récessif et est noté b
Hypothèse :
Les gamètes porteraient les caractères héréditaires et lors de la gamétogenèse des hybrides de la F1, le facteur G et le facteur b se seraient séparés.
Ce qui donnerait deux types de gamètes : les gamètes avec G et les gamètes avec b.
Vérifions cette hypothèse en établissant un échiquier de croisement (voir échiquier).
Parents : [Gris] x [blanc]
Génotypes : (G//G) x (b//b)
Gamètes : G x b
F1 : (G//b)
F1 x F1 : (G//b) x (G//b)
Gamètes : G, b x G, b
F2 : 3/4[G]+1/4[b]
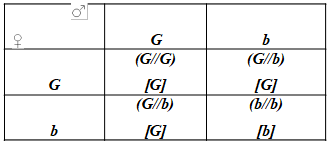
Conclusion
Les résultats théoriques étant conformes aux résultats expérimentaux, donc notre hypothèse est vérifiée
Remarque :
L'homozygote (GG) et l'hybride (Gb) ont des phénotypes identiques et des génotypes différents
√ Autre exemple : croisement de maïs :
Les parents : Mendel (1822 − 1864) prend deux lignées pures de mais qui différent par la couleur de leurs grains.
L'une a des graines noires et l'autre a des graines jaunes : ce sont les parents ou géniteurs.
Lorsque ces plantes fleurissent, il fait féconder les fleurs des plantes à graines noires avec celles des plantes à grains jaunes.
Les plantes obtenues à partir de cette fécondation sont hybrides
La génération F1 : Au niveau de cette génération F1, Mendel constate que les graines obtenus sont tous noires.
Il en conclut que le caractère noir est dominant et est noté N et le caractère jaune est récessif et noté j.
La génération F2 : Pour obtenir la génération F2, il fait semer les graines de F1 et laisse les fleurs des plantes obtenues se féconder entre elles en les protégeant d'éventuels apports extérieurs de grains de Pollen.
Les épis de la F2 ainsi obtenus présentent des graines noires et des graines jaunes distribués au hasard.
La F2 est donc hétérogène (ou polymorphe).
En comptant les grains de chaque épi de la F2, Mendel a trouvé les résultats suivants :
276 graines noires et 95 grains jaunes pour le premier épi.
173 graines noires et 55 grains jaunes pour le deuxième épi.
− Cherchons les rapports ou proportions :
∙ 1∘ épi : 276+95+ =371 ;
371/95=3.9≡4 ;
276/95=2.9≡3 ;
95/95=1
1/4(25%) de graines jaunes +3/4 de graines noires.
∙ 2∘ épi : 176+55=228 ;
228/55=4.1≡4 ;
173/55=3.1≡3
1/4(25%) de graines jaunes +3/4de graines noires.
Analyse, Interprétation (voir b)
II.1.1 Énoncé des deux 1ère lois de Mendel
− Première loi ou loi d'uniformité de F1 : Tous les individus nés de parents de lignée pure sont semblables.
(réciproquement si en F1 on obtient des individus tous semblables, on en déduit que les parents sont de lignée pure)
− Deuxième loi ou la loi de disjonction des caractères en F2 (loi de pureté des gamètes)
Les individus F2 sont différents entre eux : cette différence ne s'explique que par une disjonction des caractères allélomorphes au cours de la formation des gamètes.
Donc les gamètes ne sont jamais hybrides mais toujours pures.
II.1.2 Notion de test-cross ou de croisement test
− Un individu de phénotype récessif est obligatoirement homozygote, c'est-à-dire de lignée pure. Exemple b//b chez la souris
− Un individu de phénotype dominant peut être homozygote ou hétérozygote.
Exemple :
Les souris grises de F2 ont chacun G//G ou G//b comme génotype.
Pour savoir le génotype de ces individus, il faut recourir à la méthode dite test-cross ou test de croisement.
Pour cela, on croise l'individu de génotype inconnu avec un individu récessif car le récessif est toujours homozygote.
Parents : souris à tester (souris grises) x souris testeur (souris blanches)
Génotypes : (G//G) x (b//b)
ou (G//b) x b//b
Gamètes : G x b ou G, b x b
Résultats : (G//b) : 100%[G]
ou (G//b)+(b//b) : 50%[G]+50%[b]
Le parent testé est homozygote ou Le parent testé est hétérozygote
Deux (2) cas sont possibles :
√ Si tous les individus nés de ce croisement sont homogènes on en déduit que le parent testé n'a fourni qu'un seul type de gamète.
Il est donc homozygote.
√ Si on obtient une descendance hétérogène alors le parent testé a fourni deux types de gamètes.
Il est donc hétérozygote
N.B :
On peut aussi faire un backcross c'est-à-dire utilisé un parent récessif comme testeur.
(On dit backcross ou croisement retour)
Remarque :
Cas d'un gène létal
Un gène est dit létal (mortel) lorsque les individus homozygotes pour ce gène ne sont pas viables et meurent avant la naissance.
Exercice
− Une souris noire croisée avec une souris noire donne uniquement des souris noires et ceci quelle que soit la génération croisée.
− Une souris jaune croisée avec une souris jaune donne 2/3 de souris jaunes et 1/3 de souris noires.
− Une souris jaune croisée avec une souris noire donne 1/2 de souris jaunes et 1/2 de souris noires.
Expliquer ces résultats.
Résolution
Le 1er croisement montre que les souris noires sont de lignée pure
Le 2ième croisement montre que les souris jaunes sont des hybrides (J//n) et que l'allèle noire (n) et récessif devant l'allèle Jaune (J) qui est dominant.
L'allèle Jaune à l'état homozygote est létal ce qui fait que les souris Jaunes de génotypes (J//J) ne sont pas viables.
Dans ce cas les rapports 1/4+3/4 deviennent 1/3+2/3
Parents : souris jaunes x souris jaunes
Génotypes : (J//n) x (J//n)
Gamètes : J, n x J, n

F2=2/3 de souris Jaunes et 1/3 de souris noires
Le 3ième croisement est un test cross car il s'agit d'un croisement entre un individu de phénotype dominant et un individu récessif.
La descendance obtenue étant polymorphe 1/2[J]+1/2[n] donc les souris jaunes sont effectivement hétérozygotes et ont fournis deux types de gamètes.
II 2. Mono hybridisme sans dominance (=codominance)
Exercice d'application :
Une population de volailles dites andalouses comprend trois couleurs différentes : noire ; blanche et bleue
− Les volailles noires croisées entre elles donnent toujours des volailles noires.
− Les volailles blanches croisées entre elles donnent toujours des volailles blanches.
− Les volailles bleues croisées entre elles donnent un ensemble composé de volailles noires, blanches et bleues
− Le croisement d'une volaille blanche et d'une autre noire donne des volailles uniquement bleues.
a) En tenant compte des résultats expérimentaux.
Expliquer ce qu'on entend par lignée pure et hybride.
Classer les trois types de volailles dans ces deux groupes.
b) Les résultats statistiques d'un croisement de volailles bleues sont :
25%[noires]+50%[bleues]+25%[blanches].
Expliquer ces résultats.
c) On croise une noire et une bleue ; réaliser le tableau qui permet de prévoir les résultats.
Résolution
a) (voire définition) Les volailles noires et les volailles blanches sont de lignée pure et les volailles bleues sont hybrides.
b) Le croisement d'une volaille noire et d'une volaille blanche donne uniquement des volailles bleues qui ne ressemblent à aucun des parents mais ont un caractère intermédiaire entre noire et blanche.
On en déduit que les allèles N et B sont codominants ou à dominance intermédiaire ou encore sans dominance.
1er croisement :
Phénotypes des parents : [Noires] x [Blanches]
Génotypes : (N//N) x (B//B)
Gamètes : N x B
F1 : (N//B)
2ième croisement
F1 x F1 : [Bleues] x [Bleues]
Génotypes : (N//B) x (N//B)
Gamètes : N, B x N, B
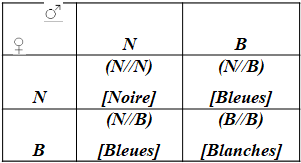
F2=1/4[Noires]+1/4[Blanches]+1/2[Bleues]
c) Phénotypes des parents : [Noires] x [Bleues]
Génotypes : (N//N) x (N//B)
Gamètes : N x N, B
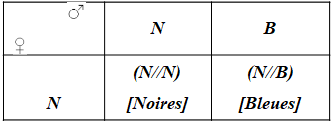
Résultats : 1/2[Noires]+1/2[Bleues]
Exemple 2 :
Cas de la belle de nuit (plante à fleurs)
On croise des plantes de lignée pure à fleurs blanches et à fleurs rouges.
On obtient 100% de plantes à fleurs roses à la F1.
Déduire les résultats obtenus à la F2.
Solution
Parents : [Blanches] x [Rouges]
Génotypes : (B//B) x (R//R)
Gamètes : B x R
F1 : (B//R)100%[Roses]
F1 x F1 : [Roses] x [Roses]
Génotypes : (B//R) x (B//R)
Gamètes : B, R x B, R
F2 : 1/4[Blanches]+1/2[Roses]+1/4[Rouges]
Auteur:
Daouda Tine

Commentaires
Anonyme (non vérifié)
mer, 04/15/2020 - 15:02
Permalien
Très important
SEYDI (non vérifié)
sam, 05/23/2020 - 07:33
Permalien
Remerciement
Fatimah (non vérifié)
dim, 06/04/2023 - 11:46
Permalien
La suite
Anonyme (non vérifié)
sam, 06/10/2023 - 00:26
Permalien
auttomatique
Anonyme (non vérifié)
sam, 06/10/2023 - 00:27
Permalien
exellent
Ajouter un commentaire