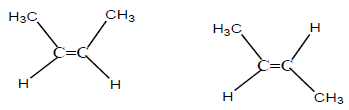Physique

Les alcools - Ts

Classe: 
Terminale
 

I. Généralités

1. Définition

Un alcool est un composé organique oxygéné qui comporte un groupe hydroxyle fixé sur un atome de carbone tétragonal.

Leur formule générale est :  $R-OH$

soit $C_{n}H_{2n+1}OH$ où $OH$ est le groupe fonctionnel des alcools appelé groupe hydroxyle

2. Nomenclature

a) Cas des monoalcools à chaine carbonée saturée 

Le nom de l'alcool dérive de celui d'un alcane de même chaine carbonée en remplaçant la terminaison $e$ par $ol$ précédé du numéro le plus petit du carbone porteur du groupe hydroxyle 

Exemples :

$CH_{3}-CH_{2}-CH_{2}OH$ : propan$-1-$ol
 
$CH_{3}-CH\left(CH_{3}\right)-CHOH-CH_{3}$ : $3-$méthylbutan$-2-$ol

Remarque : 

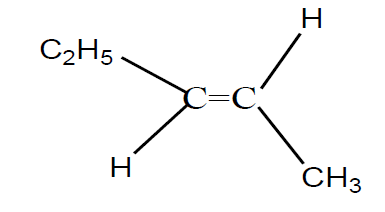
Un carbone asymétrique est un carbone tétragonal lié à quatre atomes ou groupes d'atomes différents. 
 
On le repère habituellement par un astérisque $(\ast)$

Exemple :

b) Cas des polyols 

On fait précéder le suffixe du préfixe multiplicatif adéquat (di, tri, tétra, penta...) précédé des numéros des atomes de carbone portant les groupes d'hydroxydes séparés par des virgules, l'ensemble étant mis entre tirets

Exemples : 

$CH_{2}OH-CH_{2}OH$ : éthane$-1.2-$diol
 
$CH_{2}OH-CHOH-CH_{2}OH$ : propane$-1\;,\ 2\;,\ 3-$triol ou glycérol
 
$CH_{3}-CHOH\left(CH_{3}\right)-CHOH\left(CH_{3}\right)-CH_{3}$ : $2.3-$diméthylbutane$-2.3-$diol

3. Les classes d'alcool 

La classe d'alcool est lié au nombre de groupe(s) d'alkyle(s) porté(s) par le carbone fonctionnel
 
Il existe trois classes d'alcools :
 
$-\ $ les alcools primaires : leur carbone fonctionnel est lié à un atome de carbone
 
$R-CH_{2}OH$

Exemples :   

$CH_{3}-CH_{2}OH$ : Éthanol
 
$CH_{3}-CH\left(CH\right)_{3}-CH_{2}OH$ : $2-$méthylpropan$-1-$ol
 
$-\ $ les alcools secondaires : leur carbone fonctionnel est lié à deux atomes de carbone
 
$R-CHOH-R'$

Exemple : 

$CH_{3}-CH_{2}-CHOH-CH_{3}$ : butan$-2-$ol
 
$-\ $ les alcools tertiaires : leur carbone fonctionnel est lié à trois atomes de carbone
 
$R-COHR'-R''$

Exemple :

$\left(CH_{3}\right)_{2}-COH-CH_{2}-CH_{3}$ : $2-$méthylbutan$-2-$ol

II. Propriétés des alcools

1. Les propriétés physiques

Dans les conditions ordinaires de température et de pression $(25^{\circ}C$ ; $1\,atm)$ les alcools son liquides jusqu'à $C_{12}.$
 
Au de $C_{12}$ ils sont solides
 
Les alcools en $C_{4}$ sont assez solubles dans l'eau. 
 
La solubilité diminue lorsque le nombre d'atomes de carbone augmente
 
Les alcools à très grands nombres de carbone sont pratiquement insolubles dans l'eau

2. Les propriétés chimiques :

2.1. Action du sodium

Les alcools réagissent sur le sodium métallique en donnant un dégagement de dihydrogène et un alcoolate
 
L'équation-bilan de la réaction s'écrit : 
$$\boxed{R-OH\ +\ Na\ \rightarrow\ RO^{-}\ +\ Na^{+}\ +\ \dfrac{1}{2}H_{2}}$$

2.2. Oxydation des alcools

2.2.1. Oxydation dans le dioxygène 

a) Oxydation brutale ou combustion 

Comme toute substance organique, les alcools en présence d'un excès de dioxygène ou d'air peuvent subir une combustion complète 
 
La combustion des alcools est une réaction exothermique 
 
L'équation-bilan de la réaction s'écrit : 
$$\boxed{C_{n}H_{2n+1}OH\ +\ \dfrac{3n}{2}O_{2}\ \rightarrow\ nCO_{2}\ +\ (n+1)H_{2}O}$$
 
Cette réaction explique l'emploi des alcools comme combustible ou carburants 

b) Oxydation ménagée des alcools 

Lorsque l'oxydation d'un alcool se fait sans destruction de la chaine carbonée, on dit qu'il y a oxydation ménagée 
 
$\bullet\ $ Un alcool primaire est d'abord oxydé en aldéhyde ; ensuite en acide carboxylique :
$$R-CH_{2}OH\ +\ \dfrac{1}{2}O_{2}\ \stackrel{Pt\ ou\ Cu}{\longrightarrow}\ R-CHO\ +\ H_{2}O$$
 
$$R-CHO\ +\ \dfrac{1}{2}O_{2}\ \stackrel{Pt\ ou\ Cu}{\longrightarrow}\ R-COOH$$

Remarque :

$-\ $ Le réactif de Schiff qui rosit met en évidence la formation d'un aldéhyde 
 
$-\ $ Le bleu de bromothymol qui vire en jaune met en évidence la formation d'un acide
 
$\bullet\ $ Un alcool secondaire est oxydé en cétone
$$R-CHOH-R'\ +\ \dfrac{1}{2}O_{2}\ \stackrel{Pt\ ou\ Cu}{\longrightarrow}\ R-CO-R'\ +\ H_{2}O$$ 
 
$\bullet\ $ L'alcool tertiaire ne subit pas l'oxydation ménagée car le carbone fonctionnel n'est pas lié à un atome d'hydrogène  

2.2.2. Oxydation ménagée en solution aqueuse  

Les alcools peuvent subir l'oxydation ménagée en solution aqueuse si cette oxydation est réalisée par les ions usuels $($ion dichromate $Cr_{2}O_{7}^{2-}$, ion permanganate $MnO_{4}^{-}$ en milieu acide$)$
 
L'oxydation d'un alcool primaire donne un aldéhyde lorsque l'oxydant est en défaut  en acide carboxylique lorsque l'oxydant est en excès
 
De manière générale, les couples rédox  mis en jeu sont :
 
$\ast\ \ RCHO|R-CH_{2}OH\ ;\ RCOOH|RCHO\ ;\ RCOOH|R-CH_{2}OH|R-CO-R'|R-CHOH-R'$
 
$\ast\ \ Cr_{2}O_{7}^{2-}|Cr^{3+}\ :\ Cr_{2}O_{7}^{2-}\ +\ 14H^{+}\ +\ 6e\ \leftrightarrows\ 2Cr^{3+}\ +\ 7H_{2}O$
                     rouge                                                     verte
$\ast\ \ MnO_{4}^{-}|Mn^{2+}\ :\ MnO_{4}^{-}\ +\ 8H^{+}\ +\ 5e\ \leftrightarrows\ Mn^{2+}\ +\ 4H_{2}O$
                   violette                                                  incolore                                   

Exemple : 

oxydation du propan$-2-$ol par les ions dichromates en milieu sulfurique :
 
$\left\lbrace\begin{array}{l}\left(CH_{3}-CHOH-CH_{3}\ \rightarrow\ CH_{3}-CO-CH_{3}+2H^{+}+2e\right)\\ Cr_{2}O_{7}^{2-}+14H^{+}+6e\ \rightarrow\ 2Cr^{3+}+7H_{2}O\end{array}\right.$ 
 
Demi-équations électroniques :  
 
Équation-bilan : 
 
$3CH_{3}-CHOH-CH_{3}+Cr_{2}O_{7}^{2-}+8H^{+}\ \rightarrow\ CH_{3}-CO-CH_{3}+2Cr^{3+}+7H_{2}O$

2.3. Déshydratation des alcools

2.3.1. Déshydratation intramoléculaire 

Elle conduit à un  alcène

Exemple :

$CH_{3}-CHOH-CH_{3}\stackrel{Al_{2}O_{3}\text{ à }400^{\circ}C}{\longrightarrow}CH_{3}-CH=CH_{2}+H_{2}O$
 
De manière générale, la déshydratation catalytique à la température élevée conduit à des alcènes, que l'alcool soit primaire, secondaire ou tertiaire 
 
Les alcools tertiaires se déshydratent plus facilement $($dès $200^{\circ}C)$

3.1. Déshydratation intermoléculaire 

Elle conduit à un éther-oxyde. 
 
Elle se produit à une température moins élevée
 
$R-OH+HO-R'\stackrel{Al_{2}O_{3}\text{ à }250^{\circ}C}{\longrightarrow}R-O-R'+H_{2}O$

Exemples :

$CH_{3}-OH+HO-CH_{3}\stackrel{Al_{2}O_{3}\text{ à }250^{\circ}C}{\longrightarrow}CH_{3}-O-CH_{3}+H_{2}O$ oxyde de diméthyle 
 
$CH_{3}-OH+HO-CH_{2}-CH_{3}\stackrel{Al_{2}O_{3}\text{ à }250^{\circ}C}{\longrightarrow}CH_{3}-O-CH_{2}-CH_{3}+H_{2}O$ oxyde de méthyle d'éthyle ou méthoxyéthane

3.2. Estérification

La réaction d'estérification  est la réaction d'un acide carboxylique avec un alcool
 
Elle donne naissance à une naissance à un ester  et de l'eau  
 
La réaction d'estérification est lente, athermique et réversible (elle conduit à un équilibre chimique)
 
$R-COOH\ +\ HO-R'\leftrightarrows R-COO-R'\ +\ H_{2}O$ 
acide carboxylique  alcool                    ester                  eau

Exemple :

$HCOOH\ +\ HO-CH_{2}-CH_{3}\leftrightarrows HCOO-CH_{2}-CH_{3}\ +\ H_{2}O$
acide méthanoique  éthanol                                  méthanoate d'éthyle                 eau

3.3. Hydrolyse 

La réaction d'estérification est limitée par la réaction d'hydrolyse 
 
La réaction d'hydrolyse d'un ester est son action sur l'eau.
 
Elle  donne naissance à un acide carboxylique et un alcool
 
$R-COO-R'\ +\ H_{2}O\leftrightarrows R-COOH\ +\ HO-R'$
 ester                   eau           acide carboxylique         alcool
 
Estérification et hydrolyse d'un ester sont des réactions inverses
 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Force et champ électrostatiques - 1er s

Classe: 
Première
 

Exercice 1 : pendule et force électrostatique

Une bille de masse $m=20\,g$ est suspendu à un fil de longueur $l=10\,cm.$ 
 
La bille porte une charge électrique $q$ que l'on souhaite déterminer. 
 
En approchant horizontalement une tige isolante qui porte à son extrémité une charge $q'=+10^{-6}C$, la bille est attirée par la tige et le fil fait un angle $\alpha=20^{\circ}$ par rapport à la verticale. 
 
Les charges $q$ et $q'$ sont situés à une distance $d=2\,cm.$
 
1) Faire le bilan des forces qui s'exercent sur la bille et les représenter
 
2) Écrire la condition d'équilibre
 
3) Déterminer l'intensité de la force électrostatique.
 
4) En déduire la charge $q$ portée par la bille. $\left(k=1/\left(4\pi\varepsilon_{0}\right)=9.0\cdot 10^{9}N\cdot m^{2}\cdot C^{-2}\right)$
 
 

Exercice 2

On place aux points $A$ et $B$ deux boules métalliques identiques $\left(B_{1}\right)$ et $\left(B_{2}\right)$ supposées ponctuelles. 
 
La distance entre $A$ et $B$ est égale à $2a.$ 
 
La boule $\left(B_{1}\right)$ porte la charge $-q$ et la boule $\left(B_{2}\right)$ porte la charge $+q$ $(q>0).$ 
 
On note $O$ milieu du segment $[AB]$ et $(\Delta)$ la médiatrice de $[AB]$ contenue dans le plan de la figure. 
 
Soit $M$ un point de $(\Delta)$ distant de $h$ du point $O.$ (figure 1)
 
1.1. Définir la ligne de champ. 
 
Représenter le spectre électrique des deux charges placées en $A$ et $B.$
 
1.2. Représenter les vecteurs champs électriques $\overrightarrow{E}_{A}$ et $\overrightarrow{E}_{B}$ créés respectivement par $B_{1}$ et $B_{2}$ au point $M.$
 
1.3. Exprimer la valeur de $E_{A}$ et de $E_{B}$ en fonction de $K$, $q$, $a$ et $h.$
 
Montrer que $E_{A}=E_{B}\cdot K=9\cdot 10^{9}\quad u.s.i$
 
2. On notera $\overrightarrow{E}_{M}$ le champ électrique créé par les deux boules $\left(B_{1}\right)$ et $\left(B_{2}\right)$ au point $M.$
 
2.1. Déterminer les coordonnées $E_{Mx}$ et $E_{My}$ du vecteur $\overrightarrow{E}_{M}$ dans le repère orthonormé $(M\;,\ \vec{i}\;,\ \vec{j})$ en fonction de $K$, $q$, $a$ et $h.$
 
2.2. Montrer que :
$$\overrightarrow{E}_{M}=-\dfrac{2K|q|\cos\alpha}{\left(a^{2}+h^{2}\right)}\overrightarrow{i}\;,\text{ avec }\cos\alpha=\dfrac{a}{\sqrt{a^{2}+h^{2}}}$$
 
2.3. Déduire la valeur de $\overrightarrow{E}_{M}$ au point $O.$ 
 
On donne $a=10\,cm\;,\ h=17.33\,cm\text{ et }q=0.3\mu C.$
 
 

Exercice 3

Deux charges électriques ponctuelles sont placées aux points $A$ et $B$ distants de $10\,cm.$
 
La charge placée en $A$ vaut $q_{A}=-3\cdot 10^{-9}C$ celle placée en $B$ vaut $q_{B}=4\cdot10^{-9} C.$
 
1. Énoncer la loi de Coulomb.
 
2.1. Déterminer les caractéristiques de la force exercée par $A$ sur $B$ et la force exercée par $B$ sur $A.$
 
2.2. Représenter $\overrightarrow{F}_{B/A}$ et $\overrightarrow{F}_{A/B}$
 
3. Déterminer les caractéristiques du vecteur champ électrostatique $\overrightarrow{E}$ créé par ces deux charges électriques en ces deux cas, puis les représenter.
 
3.1. Au milieu $O$ de segment $AB.$
 
3.2. En un point $M$ de la médiatrice de $AB$, situé à $5\,cm$ de $O.$
 
4. Quelles sont les caractéristiques d'un champ électrique uniforme (donner un schéma de spectre de champ)
 
 

Exercice 4

Trois pendules électrostatiques sont formés de trois petites sphères identiques $A$, $B$ et $C$, supposées ponctuelles, de même masse $m=10.0\,g$, suspendues par des fils de masses négligeables à un support horizontal de telle façon que leurs points d'attache respectifs $A'$, $B'$ et ce sont régulièrement espacés : $A'B'=B'C'$ (voir Figure ci-dessous).
 
 
Les deux fils supportant les sphères $A$ et $C$ sont de même longueur $l$, égale à $25.0\,cm$, et forment tous les deux un angle $\alpha$ avec la verticale. 
 
Le fil supportant la sphère $B$ est vertical et d'une longueur $l'$ telle que les centres de $A$, $B$ et $C$ sont alignés dans un même plan horizontal. 
 
Les sphères $A$ et $C$ portent chacune la même charge : $q=+200\,nC$
 
La sphère $B$ porte une charge $q'$ de valeur double de celle de $q.$
 
Données : 
 
Distance $d$ entre les centres de $A$ et $B$ $($égale à la distance entre les centres de $B$ et $C)$ : $d=10.0\,cm.$
 
Accélération de la pesanteur : $g=9.81\,m\cdot s^{-2}.$
 
Interaction de Coulomb : $k=9.00\cdot10\,u\ S.I$  
 
Interaction de Newton : $G=6.67\cdot10^{-11}u\ S.I$
 
On néglige les actions de l'air, ainsi que les interactions gravitationnelles entre les sphères.
 
1. Quel est le signe de $q'$ ? 
 
Justifier.
 
2. On s'intéresse à l'équilibre de $A.$
 
2.1. Faire le bilan des forces qui s'exercent sur $A$, sans faire intervenir, pour simplifier, l'action de $C.$
 
2.2. Représenter ces forces sur un schéma, sans souci d'échelle mais en respectant leurs directions, leurs sens et leurs points d'application.
 
2.3. Énoncer la condition d'équilibre de $A.$
 
2.4. En déduire la valeur de l'angle $\alpha.$
 
2.5. Déterminer les valeurs des forces qui s'exercent sur $A.$
 
3. On s'intéresse à l'équilibre de $B.$
 
3.1. Faire le bilan des forces qui s'exercent sur $B.$
 
3.2. Représenter ces forces sur un schéma, sans souci d'échelle mais en respectant leurs directions, leurs sens et leurs points d'application.
 
3.3. Déterminer les valeurs des forces qui s'exercent sur $B.$

Exercice 5

Une tige isolante $AB$ $(AB=20\,cm)$ est inclinée d'un angle $\alpha=30^{\circ}$ avec l'horizontale.
 
1. On fixe en $A$ une charge $q_{1}=-10\,nC$, en $B$ une charge $q_{2}=10\,nC.$
 
Déterminer les caractéristiques du vecteur champ électrostatique au point $C$ situé sur la tige $AB$ à $5\,cm$ de $A.$
 
2. Une petite sphère $(S)$ portant une charge $q=30\,nC$, de masse $m$, peut coulisser sans frottement sur la tige $AB$, elle s'immobilise en $C.$
 
a) Faire le bilan des forces qui s'exercent sur la sphère $(S)$ ; les représenter.
 
b) En appliquant la condition d'équilibre de la sphère, calculer la masse $m$ et la valeur de la réaction de la tige.
 
On donne $g=10\,N\cdot Kg^{-1}.$
 
3. En maintenant la tige $AB$ horizontalement, la sphère reste-t-elle immobile ? 
 
Si non dans quel sens va-t-elle se déplacer ?
 
 

Exercice 6

On donne la constante électrostatique $K=9\cdot10^{9}\ u.s.i.$
 
Le schéma de la figure 1 représente deux pendules électrostatiques, de même longueur $l=20\,cm$, portant, respectivement, à leurs extrémités libres deux boules supposées ponctuelles $A$ et $B$ de même masse et de charges respectives $q_{A}=-q_{B}=2\mu C.$
 
 
Lorsqu'on rapproche les pendules l'un de l'autre, ils prennent la position d'équilibre indiquée sur le schéma de la figure
 
À l'équilibre, chacun des deux pendules fait un angle $\alpha$ très petit avec $\sin\alpha=0.1.$ 
 
La distance séparant les deux points d'attache $O$ et $O'$ des deux pendules est $OO'=14\,cm.$
 
1. Calculer la distance $AB$ à l'équilibre.
 
2.1. Représenter toutes les forces exercées sur les boules $A$ et $B$
 
2.2. Déterminer la valeur de la force de l'interaction électrique existant entre les boules $A$ et $B.$

Exercice 7

Deux points $A$ et $B$ sont situés sur la circonférence d'un cercle de centre $O$ et de rayon $R=6\,cm.$ 
 
En $A$ et $B$ on place respectivement deux boules ponctuelles chargées de même charge $q_{A}=q_{B}=2\cdot10^{-7}C$ et de masses négligeables.
 
1. Représenter les forces électriques $\overrightarrow{F}_{A/B}$ et $\overrightarrow{F}_{B/A}$ qui constituent l'interaction électrique existant entre $q_{A}$ et $q_{B}.$
 
Donner les caractéristiques de $\overrightarrow{F}_{A/B}$
 
2.1. Représenter, au point $O$, les vecteurs champs électrostatiques de $\overrightarrow{E}_{A}$ et $\overrightarrow{E}_{B}$ créés respectivement par les charges $q_{A}$ et $q_{B}.$ 
 
Calculer la valeur de $\overrightarrow{E}_{A}$
 
2.2. Déterminer les caractéristiques du vecteur champ électrostatique $\overrightarrow{E}_{O}=\overrightarrow{E}_{A}+\overrightarrow{E}_{B}$ créé par l'ensemble des deux charges au point $O.$
 
3. Au point $O$, on place un corps ponctuel $(C)$ de masse $m$ qui porte une charge de valeur absolue $|Q_{0}|=2\cdot10^{-8}C$, il prend une position d'équilibre stable.
 
3.1. Représenter la force $\overrightarrow{F}$ exercée par $q_{A}$ et $q_{B}$ sur la charge $Q_{0}.$ 
 
Quel est le signe de $Q_{0}$ ? 
 
Justifier la réponse.
 
3.2 Écrire la condition d'équilibre du corps ponctuel $(C).$ 
 
Calculer la masse $m$ du corps
 
 

Exercice 8

Une sphère de centre $S$ est attachée au point $O$ par un fil isolant de masse négligeable et de longueur $l=40\,cm.$
 
La sphère, de masse $m=2\cdot10^{-2}kg$, porte une charge $q.$ 
$$g=10\,N\cdot kg^{-1}$$
 
 
1. On la soumet à un champ électrique uniforme $E$, horizontal, orienté comme indique la figure. 
 
Le fil s'incline alors d'un angle $\alpha=10^{\circ}$ par à rapport à la verticale. 
 
En déduire la valeur de la charge $q.$ 
 
Intensité du champ électrostatique $E=10^{3}V\cdot m^{-1}$
 
2. On superpose au champ électrostatique précédent, un autre champ électrostatique uniforme $E'$ vertical.
 
Quels doivent être le sens et l'intensité du champ $E'$ pour que le fil s'incline sur la verticale d'un angle $\alpha=20^{\circ}$
 
3. Quelle serait l'inclinaison $\alpha'$ si l'on changeait le sens de $E'$ sans modifier son intensité

Exercice 9

Deux petites sphères métalliques et identiques sont fixées aux extrémités $A$ et $B$ d'une barre. 
 
On a : $AO=OB=l$
 
Les sphères sont chargées et portent respectivement les charges $q$ et $-q.$ 
 
On introduit ce dispositif entre deux plaques parallèles. 
 
Lorsque celles-ci sont branchées à la terre, la barre $AOB$ est parallèle aux plaques, et le fil n'est pas tordu. 
 
Lorsque les plaques sont branchées à la terre, la barre $AOB$ est parallèle aux plaques, et le fil n'est pas tordu. 
 
Lorsque les plaques sont branchées à un générateur haute tension, il existe un champ électrostatique uniforme $\overrightarrow{E}$ perpendiculaire aux plaques. 
 
La barre $AOB$ fait alors un angle $\alpha$ avec la direction précédente et reste horizontale
 
 
1. Calculer en fonction de $l$, $\alpha$, $q$ et $E$ le moment des forces électrostatiques par rapport à l'axe de rotation du dispositif.
 
2. Calculer le moment du poids du système par rapport à l'axe de rotation.
 
3. Le dispositif étant en équilibre, le fil de torsion exerce des actions mécaniques dont le moment par rapport à l'axe de rotation est proportionnel à l'angle de rotation $\alpha$ :
 
$|M_{\Delta}|=C\alpha$ Avec $C=13.5\cdot10^{-7}N\cdot m\cdot rad^{-1}.$
 
Calculer $q$ sachant que : $E=272\,V\cdot m^{-1}$ ; $l=15\,cm$ ; $\alpha=\dfrac{\pi}{6}.$

Exercice 10

En deux points $A$ et $B$ tels que $OA=OB=d$, sont placées deux charges ponctuelles égales $q$ et de même signe.
 
On se propose de déterminer le champ électrique crée par ces deux charges en un point $M$ tel que $OM=x.$
 
Établir, en fonction de $x$, $d$ et $q$ ; l'expression du champ électrique crée par les deux charges au point $M$ dans chacun des cas représentés sur les schémas suivants :
 
1) Le point $M$ se trouve sur le segment $[AB]$ entre les points $O$ et $B$ :
 
 
2) Le point $M$ se trouve dans l'alignement de $AB$ à l'extérieur du segment $[AB]$ du côté du point $B$ :
 
 
3) Le point $M$ est situé sur la médiatrice du segment $[AB]$ :
 
 

Exercice 11

Une charge ponctuelle $Q=-40\,nC$ est placée au sommet $A$ d'un carré $ABCD$ de $2.0\,cm$ de côté
 
1. Déterminer les caractéristiques (valeur, direction et sens) des champs électriques $\overrightarrow{E}_{B}$ et $\overrightarrow{E}_{C}$ créés par cette
charge aux points $B$ et $C.$
 
2. Représenter ces champs
 
3. Représenter quelques lignes de champs autour du point $A.$
 
4. On place une charge ponctuelle $q=-10\,nC$ au point $C.$
 
4.1. Déterminer les caractéristiques (valeur, direction et sens) de la force électrique s'exerçant sur cette charge.
 
4.2. Représenter cette force
 
4.3. Représenter, à la même échelle, la force électrique qui s'exerce sur la charge $Q.$
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Sidy Mouhamed Ndiaye

Série d'exercices : La calorimétrie - 1er s

Classe: 
Première
 

Exercice 1

1) Calculer la quantité de chaleur nécessaire pour élever de $20^{\circ}C$ à $80^{\circ}C$ une masse égale à $1$ tonne d'eau.
 
2) Si cette énergie calorifique pouvait être transformée en énergie potentielle de pesanteur, à quelle altitude $z$ pourrait-on soulever cette tonne d'eau ?

Exercice 2

Un calorimètre contient une masse $m_{1}=95\,g$ d'eau à $t_{1}=20^{\circ}C.$
 
On ajoute une masse d'eau $m_{2}=100\,g$ d'eau à $t_{2}=50^{\circ}C.$
 
1) Si on néglige l'intervention du calorimètre, calculer la température finale $t_{f}.$
 
2) En réalité la température finale vaut $t_{f'}=31.3^{\circ}C.$
 
Calculer la valeur en eau $\mu$

Exercice 3

1) Dans un calorimètre, à la température ambiante $t_{a}=15.5^{\circ}C$ on verse une masse d'eau $m_{e}=90\,g$ d'eau à $t_{e}=25^{\circ}C.$ 
 
La température d'équilibre vaut $t_{1}=24.5^{\circ}C.$
 
Calculer la valeur en eau $\mu$ du calorimètre.
 
2) Immédiatement après, on plonge dans l'eau du calorimètre une masse platine $m_{p}=100\,g$ à $t_{p}=104^{\circ}C.$ 
 
La nouvelle température d'équilibre $t_{2}=27.7^{\circ}C.$ 
 
Calculer la chaleur massique du platine.
 
3) Dans la foulée, on ajoute une masse $m=23\,g$ d'eau à la température ambiante $t_{a}.$ 
 
Calculer la température finale $t_{3}.$

Exercice 4

Dans un calorimètre en cuivre de masse $m_{c}=100\,g$ et qui contient une masse d'eau $m_{e}=200\,g$ à $t_{e}=4^{\circ}C$, on introduit une masse $m_{1}=300\,g$ de cuivre à $t_{1}=-20^{\circ}C.$
 
1) On agite pour atteindre l'équilibre thermique : calculer la température finale $t_{f}.$
 
2) Montrer que si le cuivre introduit est à la température $t_{2}=-50^{\circ}C$, une partie de l'eau congèle.
 
Calculer la masse de glace formée $mg.$
 
Chaleur massique du cuivre : $395\,J\cdot kg^{-1}\cdot K^{-1}$

Exercice 5

Dans l'enceinte adiabatique d'un calorimètre à la température $t_{c}=15^{\circ}C$, on introduit un bloc de cuivre de masse $m_{1}=200\,g$ à la température $t_{1}=100^{\circ}C.$ 
 
La température finale vaut $t_{f}=20^{\circ}C.$
 
1) Calculer la capacité calorifique $C_{cal}$ du calorimètre.
 
2) On introduit d'autre part, dans une expérience similaire, une masse $m_{2}=100\,g$ d'alliage pris à $t_{2}=100^{\circ}C.$ 
 
La température finale est la même.
 
Calculer la chaleur massique de l'alliage

Exercice 6

Pour mesurer le pouvoir calorifique $P_{C}$ d'un combustible solide, on place $1\,g$ de ce solide dans un récipient $A$ hermétiquement clos et contenant assez de dioxygène pour faire sa combustion totale. 
 
Le récipient $A$ est placé dans un calorimètre. 
 
On réalise, dans les mêmes conditions expérimentales, deux expériences successives :
 
1) On brûle $m=1\,g$ de naphtalène $(PC=40\ 500\,kJ/kg)$, et on note la température du calorimètre : avant la combustion : 
 
$t_{0}=18.3^{\circ}C$ et après la combustion : $t_{1}=21.4^{\circ}C$
 
Déduire de cette expérience la capacité calorifique $C$ du calorimètre $+$ récipient.
 
2) On brûle $m=1\,g$ de houille, de pouvoir calorifique inconnu $P_{C'}$, et on note la température du calorimètre : 
 
avant la combustion : $t_{0}=18.3^{\circ}C$ et après la combustion : $t_{2}=20.8^{\circ}C$
 
Déterminer l'expression littérale de $P_{C'}$, puis faire l'application numérique

Exercice 7

1) Un calorimètre contient $100\,g$ d'eau à $18^{\circ}C.$ 
 
On y verse $80\,g$ d'eau à $60^{\circ}C.$
 
Quelle serait la température d'équilibre si la capacité thermique du calorimètre et de ses accessoires était négligeable ?
 
2) La température d'équilibre est au fait $35.9^{\circ}C.$ 
 
En déduire la capacité thermique du colorimètre et de ces accessoires.
 
3) On considère de nouveau ce colorimètre qui contient $100\,g$ d'eau à $18^{\circ}C.$ 
 
On y plonge un morceau de cuivre de masse $20\,g$ initialement placé dans de l'eau en ébullition. 
 
La température d'équilibre s'établit à $19.4^{\circ}C.$ 
 
Calculer la chaleur massique du cuivre
 
4) On considère encore le même calorimètre contenant $100\,g$ d'eau à $18^{\circ}C.$ 
 
On y plonge un morceau d'aluminium de masse $30.2\,g$ initialement à $100^{\circ}C$ et de chaleur massique $920\,J\cdot kg^{-1}\cdot k^{-1}.$
 
Déterminer la température d'équilibre.
 
5) L'état initial restant le même : le calorimètre contenant $100\,g$ d'eau à $18^{\circ}C$ ; on y introduit un glaçon de masse $25\,g$ à $O^{\circ}C.$
 
Calculer la température d'équilibre
 
6) L'état initial est encore le calorimètre contenant $100\,g$ d'eau à $18^{\circ}C.$ 
 
On y introduit maintenant un glaçon de masse $25\,g$ provenant d'un congélateur à la température de $-18^{\circ}C.$ 
 
Quelle est la température d'équilibre ?
 
On donne : 
 
$-\ $ chaleur massique de la glace $C_{g}=2.10\cdot 10^{3}J\cdot Kg^{-1}\cdot K^{-1}$
 
$-\ $ chaleur massique de l'eau : $C_{e}=4185\,J\cdot kg^{-1}\cdot K^{-1}$
 
$-\ $ chaleur latente de fusion de la glace : $L_{f}=333.7\,kJ\cdot kg^{-1}$

Exercice 8

Afin de déterminer la capacité thermique massique $c_{1}$ d'une brique non poreuse, on réalise l'étude suivante sur un échantillon de masse $m_{1}=100\,g.$
 
Pour cela, on dispose d'un calorimètre de capacité thermique $\mu=209\,J\cdot^{\circ}C^{-1}$ contenant une masse d'eau $m_{2}=400\,g$ de capacité thermique massique $c_{2}=4.18\,J\cdot g^{-1}\cdot^{\circ}C^{-1}$, l'ensemble étant à la température $\theta_{2}=16.0^{\circ}C.$
 
L'échantillon est placé dans une étuve dont la température est fixée à, $\theta_{1}=98.0^{\circ}C.$ 
 
Une fois l'équilibre thermique réalisé, on sort l'échantillon et on le plonge rapidement dans le calorimètre. 
 
La température finale d'équilibre est $\theta_{F}=19.9^{\circ}C.$
 
1) Donner l'expression littérale de la quantité de chaleur cédée par la brique au système {eau $+$ calorimètre} en fonction de $m_{1}$, $c_{1}$ et des températures $\theta_{1}$ et $\theta_{F}.$
 
2) Donner l'expression littérale de la quantité de chaleur reçue par le système {eau $+$ calorimètre) en fonction de $m_{2}$, $c_{2}$, $\mu$ et des températures $\theta_{2}$ et $\theta_{F}.$
 
3) Déterminer la capacité thermique massique $c_{1}$ de la brique $($On exprimera tout d'abord cette capacité en fonction des grandeurs $m_{1}$, $m_{2}$, $c_{2}$, $\mu$, $\theta_{2}$, $\theta_{1}$, $\theta_{F}$ et on la calculera$).$

Remarque : 

On négligera tout échange de chaleur avec le milieu extérieur

Exercice 9

1) Bain à $37^{\circ}C$
 
On désire obtenir un bain d'eau tiède à la température $\theta=37^{\circ}C$, d'un volume total $V=250$ litres, en mélangeant un volume $V_{1}$ d'eau chaude à la température initiale $\theta_{1}=70^{\circ}C$ et un volume $V_{2}$ d'eau froide à la température initiale $\theta_{2}=15^{\circ}C.$
 
Déterminer $V_{1}$ et $V_{2}$ en supposant négligeables toutes les fuites thermiques lors du mélange.
 
2) Chaleur massique du plomb
 
On sort un bloc de plomb de masse $m_{1}=280\,g$ d'une étuve à la température $\theta_{1}=98^{\circ}C.$ 
 
On le plonge dans un calorimètre de capacité thermique $C=209\,J\cdot K^{-1}$ contenant une masse $m_{2}=350\,g$ d'eau. 
 
L'ensemble est à la température initiale $\theta_{2}=16^{\circ}C.$ 
 
On mesure la température d'équilibre thermique $\theta_{e}=17.7^{\circ}C.$
 
Déterminer la chaleur massique du plomb.

Exercice 10

1) Bloc de fer plongé dans l'eau
 
Un morceau de fer de masse $m_{1}=500\,g$ est sorti d'un congélateur à la température $\theta_{1}=-30^{\circ}C.$ 
 
Il est plongé dans un calorimètre, de capacité thermique négligeable, contenant une masse $m_{2}=200\,g$ d'eau à la température initiale $\theta_{2}=4^{\circ}C.$
 
Déterminer l'état final d'équilibre du système (température finale, masse des différents corps présents dans le calorimètre).
 
2) Fusion d'un glaçon
 
Un calorimètre de capacité thermique $C=150\,J\cdot K^{-1}$ contient une masse $m_{1}=200\,g$ d'eau à la température initiale $\theta_{1}=50^{\circ}C.$
 
On y place un glaçon de masse $m_{2}=160\,g$ sortant du congélateur à la température $\theta_{2}=-23^{\circ}C.$
 
Déterminer l'état final d'équilibre du système (température finale, masse des différents corps présents dans le calorimètre).

Exercice 11 : Détermination de la capacité thermique d'un calorimètre

Un calorimètre contient une masse $m_{1}=250\,g$ d'eau. 
 
La température initiale de l'ensemble est $\theta_{1}=18^{\circ}C.$ 
 
On ajoute une masse $m_{2}=300\,g$ d'eau à la température $\theta_{2}=80^{\circ}C.$
 
1) Quelle serait la température d'équilibre thermique $\theta_{e}$ de l'ensemble si la capacité thermique du calorimètre et de ses accessoires était négligeable ?
 
2) On mesure en fait une température d'équilibre thermique $\theta_{e}=50^{\circ}C.$ 
 
Déterminer la capacité thermique $C$ du calorimètre et de ses accessoires.

Données :

Masse volumique de l'eau : $\mu=1000\,kg\cdot m^{-3}.$
 
Capacité thermique massique de l'eau : $c_{e}=4185\,J\cdot kg^{-1}\cdot K^{-1}.$
 
Capacité thermique massique de la glace : $c_{g}=2090\,J\cdot kg^{-1}\cdot K^{-1}.$
 
Capacité thermique massique du fer : $c_{Fe}=460\,J\cdot kg^{-1}\cdot K^{-1}.$
 
Chaleur latente massique de fusion de la glace : $L_{f}=3.34\cdot 10^{5}J\cdot kg^{-1}.$
 
Chaleur latente massique de solidification de l'eau : $L_{s}=-3.34\cdot 10^{5}J\cdot kg^{-1}.$

Exercice 12

A. Mesure de la capacité thermique d'un calorimètre.
 
On verse un volume $V_{0}=200\,mL$ d'eau dans un calorimètre et on mesure la température de l'ensemble après quelques minutes : $\theta_{0}=20.0^{\circ}C.$ 
 
On ajoute alors au contenu du calorimètre une masse : $m=250\,g$ d'eau à la température : $\theta_{1}=60.0^{\circ}C.$
 
1. Déterminer la valeur $\theta_{2}$ de la température finale de l'eau après mélange, si l'on suppose que toute l'énergie thermique cédée par l'eau chaude a été gagnée par l'eau froide.
 
2. La température d'équilibre thermique mesurée est en réalité : $\theta'_{2}=38.0^{\circ}C.$
 
2.1. Déterminer la valeur de l'énergie thermique gagnée par le calorimètre.
 
2.2. En déduire la valeur de la capacité thermique du calorimètre.
 
B. Mesure de la chaleur latente $L_{v}$ de vaporisation de l'eau.
 
On verse un volume $V'_{0}=450\,mL$ d'eau dans un calorimètre de capacité thermique $\mu=100\,J\cdot^{\circ}C^{-1}.$ 
 
On mesure la température de l'ensemble après quelques minutes : $\theta_{0}=20.0^{\circ}C.$ 
 
On ajoute alors au contenu du calorimètre une masse : $m'=20.0\,g$ de vapeur d'eau à la température : $\theta_{3}=100^{\circ}C.$ 
 
Toute la vapeur se condense. 
 
Après équilibre thermique, on mesure une température de l'ensemble {eau liquide $+$ calorimètre} de $\theta_{4}=45.2^{\circ}C.$
 
1. Exprimer, en fonction des données, l'énergie thermique échangée par le calorimètre et les $450\,mL$ d'eau liquide.
 
Quelle est le signe de cette énergie ?
 
2. Exprimer, en fonction des données et de $L_{v}$, l'énergie thermique échangée par la vapeur d'eau.
 
Quel est le signe de cette énergie ?
 
3. Calculer une valeur numérique de $L_{v}.$

Données : 

$C_{eau}\cong 4\ 180\,J\cdot kg^{-1}\cdot^{\circ}C^{-1}$ ;
 
$C_{vapeur}\text{ d'eau}\cong 1\ 410\,J\cdot kg^{-1}\cdot^{\circ}C^{-1}.$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Réflexion et réfraction de la lumière - 4e

Classe: 
Quatrième
 

Exercice 1

Complétons les phrases suivantes par les mots ou groupe de mots qui conviennent :
 
Un objet qui possède une surface parfaitement polie est appelé miroir plan, il renvoie la lumière dans une direction privilégiée : ce phénomène est appelé réflexion spéculaire.
 
Le renvoi de la lumière par un corps éclairé est appelé réflexion.
 
Les rayons incident et réfléchi se trouvent dans plan d'incidence.
 
L'angle d'incidence est l'angle que fait la normale et le rayon incident tandis que l'angle de réflexion est l'angle entre la normale et le rayon réfléchi. Ces deux angles sont égaux.
 

Exercice 2

Un objet lumineux ponctuel $A$ est placé à $20\;cm$ d'un miroir de grande dimension.
 
Il envoie un rayon lumineux qui fait un angle de $30^{\circ}$ avec la normale.
 
1) Construisons l'image $A'$ de cet objet donnée par le miroir.
 
On choisit comme échelle : $1\;cm$ sur le graphique représente $5\;cm$

 

 
2) Donnons la position de son image.
 
L'image est virtuelle et se trouve dans le prolongement du rayon réfléchi.
 
Elle est le symétrique de l'objet par rapport au plan du miroir.
 
Déterminons l'angle de réflexion.
 
Le rayon lumineux ou rayon incident fait un angle $i=30^{\circ}.$
 
Or, d'après la loi de Descartes sur la réflexion, l'angle de réflexion $r$ est égal à l'angle d'incidence $i.$
 
Donc, le rayon réfléchi par ce miroir fera un angle $r=30^{\circ}$ par rapport à la normale.

Exercice 3

Un objet $AB$ de hauteur $h=2\;cm$ est placé à $1\;m$ d'un miroir perpendiculairement au plan de ce miroir.
 
1) Traçons la marche de deux rayons issus de $A$ et deux rayons issus de $B.$

 

 
2) Les caractéristiques (position, hauteur et sens) de l'image $A'B'\ $ de $\ AB$ donnée par ce miroir sont :
 
$-\ $ image virtuelle
 
$-\ $ image  est le symétrique de l'objet par rapport au plan du miroir
 
$-\ $ image est de sens opposé au sens de l'objet
 
$-\ $ image est de même hauteur que l'objet $(h=2\;cm)$

Exercice 4

Une personne de hauteur $1.80\;m$ est à $1\;m$ d'une armoire à glace.
 
1) Son image se trouve à $1\;m$ de la glace.
 
En effet, on sait que l'image est virtuelle et est symétrique à cette personne par rapport à la glace.
 
Donc, si cette personne est à $1\;m$ de la glace alors, son image virtuelle sera elle aussi à $1\;m$ de la glace.
 
2) Déterminons alors la distance qui sépare cette personne de sa nouvelle image lorsqu'elle recule de $0.5\;m$
 
En reculant de $0.5\;m$, cette personne se trouve donc à une distance de $1+0.5=1.5\;m$ de la glace.
 
Sa nouvelle image sera alors à cette même distance de la glace ; c'est-à-dire $1.5\;m$
 
Ainsi, la distance qui sépare cette personne de sa nouvelle image sera donnée par :
$$d=1.5+1.5=3\;m$$
3) La tête du personnage n'est pas superposable à son image car la glace de cette armoire est un miroir plan.
 
Ainsi, par exemple l'œil gauche de cette personne donne un œil droit pour image et pareil pour l'œil droit.

Exercice 5

Recopions et complétons les phrases suivantes par les mots ou groupes de mots suivants :
 
angle d'incidence, rayon réfracté, angle de réflexion, plan d'incidence, réfraction, angle réfracté, rayon incident, réflexion, angle d'incidence, rayon réfléchi.
 
Un rayon lumineux arrive à la surface de séparation de deux milieux et faisant un angle $\widehat{i}$ avec la normale à la surface de séparation.
 
L'angle $\widehat{i}$ est appelé angle d'incidence.
 
Le rayon arrivant sur la surface de séparation des deux milieux s'appelle le rayon incident.
 
Il subit une réfraction et une réflexion.
 
Le rayon renvoyé par la surface s'appelle le rayon réfléchi.
 
Le rayon traversant la surface s'appelle le rayon incident, l'angle qu'il forme avec la normale s'appelle angle réfracté.

Exercice 6

Identifions les rayons $1\;,\ 2\ $ et $\ 3$

 

 
$1\ : $ rayon incident
 
$2\ : $ rayon réfracté
 
$3\ : $ rayon réfléchi

Exercice 7

Un faisceau laser passe de l'air dans l'eau, comme dans le schéma ci-dessous.
 
On dit que cette lumière est réfractée.
 
En effet, l'eau et l'air étant deux milieux différents alors, le passage d'un faisceau laser de l'air dans l'eau entraine un déviation du faisceau due au changement de milieu. 
 
Traçons le rayon réfléchi puis complétons le schéma en indiquant les angles d'incidence et de réfraction.

 

 
$i_{1}$ est l'angle d'incidence
 
$i_{2}$ est l'angle de réfraction
 
$r$ est l'angle de réflexion
 

 

 
 
Auteur: 
Aliou ndiaye

Solution des exercices : Source et récepteur de lumière - 4e

Classe: 
Quatrième
 

Exercice 1

Mettons une croix dans la case correspondant à la bonne réponse.
 
1) Un objet qui produit et émet de la lumière est :
 
$\boxed{\times}\ $ une source primaire
 
$\boxed{\ }\ $ une source secondaire
 
$\boxed{\ }\ $ une source électrique
 
2) Un objet qui émet de la lumière reçue est :
 
$\boxed{\ }\ $ une source réelle
 
$\boxed{\ }\ $ une source thermique
 
$\boxed{\times}\ $ une source apparente
 
3) Le soleil est une source :
 
$\boxed{\ }\ $ apparente
 
$\boxed{\times}\ $ réelle
 
$\boxed{\ }\ $ artificielle
 
4) La lune est une source :
 
$\boxed{\ }\ $ artificielle
 
$\boxed{\ }\ $ primaire
 
$\boxed{\times}\ $ secondaire
 

Exercice 2

On considère les objets suivants :
 
1) cahier ; 2) flamme de bougie ; 3) lune ; 4) écran de télévision ; 5) soleil ;
 
6) sol ; 7) miroir ; 8) mur ; 9) œil ; 10) ciel ; 11) diode électroluminescente ;
 
12) éclair ; 13) charbon incandescent ; 14) lampe à néon ; 15) comète ;
 
16) étoile ;  17) habit ; 18) tableau ; 19) panneau solaire ; 20) plaque de zinc ;
 
21) pellicule photo.
 
Écrivons le numéro de chacun de ces objets dans la (ou les) colonne(s) qui convient (ou conviennent) :
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Sources réelles}&\text{Sources réelles}&\text{Sources}&\text{Récepteurs}&\text{Récepteurs}&\text{Objets}\\  \text{Naturelles}&\text{Artificielles}&\text{secondaires}&\text{Naturels}&\text{Artificiels}&\text{éclairés}\\ \hline 5\;;\ 12&2\;;\ 4&3\;;\ 6&6\;;\ 9&17\;;\ 19&1\;;\ 8\\ 13\;;\ 16&11\;;\ 14&7\;;\ 15&10&21&18\\ &&19\;;\ 20& &&\\ \hline \end{array}$$
 
Auteur: 
Aliou ndiaye

Solution exercices : Propagation rectiligne de la lumière - 4e

Classe: 
Quatrième
 

Exercice 1 Contrôle de connaissances

Recopions et complétons les phrases suivantes par les mots suivants : opaque, transparent, rectiligne, et translucide.
 
Dans un milieu transparent et homogène la lumière se propage de façon rectiligne.
 
Un milieu translucide laisse passer une partie de la lumière mais ne permet pas de distinguer les corps qui émettent cette lumière.
 
Un objet éclairé par une source placé derrière un écran transparent peut être distingué nettement. Un milieu opaque ne peut être traversé par la lumière.
 

Exercice 2

Recopions et complétons le tableau par "OUI" ou "NON"
$$\begin{array}{|l|l|l|l|} \hline \text{Corps}&\text{Transparent}&\text{Translucide}&\text{Opaque}\\ \hline \text{Eau}&\text{OUI}&\text{NON}&\text{NON}\\ \hline \text{Bois}&\text{NON}&\text{NON}&\text{OUI} \\ \hline \text{Papier huilé}&\text{NON}&\text{OUI}&\text{NON}\\ \hline \text{Vitre non teintée}&\text{OUI}&\text{NON}&\text{NON}\\ \hline\text{Huile}&\text{NON}&\text{OUI}&\text{NON}\\ \hline \text{Lait}&\text{NON}&\text{OUI}&\text{NON}\\ \hline \text{Paupière}&\text{NON}&\text{NON}&\text{OUI}\\ \hline \end{array}$$

Exercice 3

En 1850, Léon Foucault, astronome et physicien français du $19^{\text{ème}}$ siècle, démontre que la lumière se déplace moins vite dans l'eau puis, 12 ans plus tard, il évalue que la vitesse de la lumière dans l'air est d'environ de 300000 kilomètres par seconde avec une précision très satisfaisante.
 
1) Calculons le temps mis par la lumière pour parcourir un mètre dans l'air.
 
Soit $v$ la vitesse de la lumière dans l'air, $d$ la distance parcourue et $t$ le temps mis.
 
On a : $v=\dfrac{d}{t}$ ; ce qui veut dire que, $v\times t=d$
 
Par suite, $t=\dfrac{d}{v}\ $ avec $\ d=1\;m=10^{-3}\;km\ $ et $\ v=300000\;km.s^{-1}$
 
A.N : $t=\dfrac{10^{-3}}{300000}=3.333\;10^{-9}$
 
D'où, $\boxed{t=3.333\;10^{-9}\;s}$
 
2) Déterminons la distance parcourue par la lumière pendant une année dans l'air.
 
On a : $d=v\times t\ $ avec $\ t=1\;\text{année}$
 
Convertissons le temps $t$ en seconde.
 
On sait que : $1\;\text{année}=365\;\text{jours}\ $ et $\ 1\;\text{jour}=24\;h$
 
Donc, $1\;\text{année}=365\times 24\;h=8760\;h$ or, $1\;h=60\;mn\ $ et $\ 1\;mn=60\;s$
 
Par suite, $1\;\text{année}=8760\times 60\times 60=31536000\;s$
 
Ainsi, $d=300000\times 31536000=9460800000000$
 
D'où, $\boxed{d=9.4608\;10^{12}\;km}$
 
Cette longueur représente une année lumière.
 
3) Le soleil se trouve à environ $150000000\;km$ de la terre.
 
Calculons le temps que la lumière émise par le soleil met pour nous parvenir sur la terre.
 
Soit : $t=\dfrac{d}{v}\ $ avec $\ d=150000000\;km\ $ et $\ v=300000\;km.s^{-1}$
 
A.N : $t=\dfrac{150000000}{300000}=500$
 
Ainsi, $\boxed{t=500\;s=8\;mn\ 20\;s}$
 
Donc, la lumière émise par le soleil met $8\;mn\ 20\;s$ pour nous parvenir sur la terre.

Exercice 4

Un objet $AB$ est devant une chambre noire.
 
Reproduisons le schéma et traçons les rayons lumineux partant de $A\ $ et $\ B$ et pénétrant dans la chambre noire.

 

 
Les rayons plus clairs délimitent l'intervalle de propagation des rayons lumineux pénétrant dans la chambre.

Exercice 5

Considérons la figure ci-dessous

 

 
Les types de faisceaux lumineux observés sont :
 
$A\ $ : faisceaux divergents
 
$B\ $ : faisceaux parallèles
 
$C\ $ : faisceaux convergents

Exercice 6

Annotation

 

 
Signification des numéros indiqués :
 
$1-\ $ ombre propre
 
$2-\ $ cône d'ombre
 
$3-\ $ ombre portée

 

 
Signification des numéros indiqués :
 
$1-\ $ pénombre propre
 
$2-\ $ ombre propre
 
$3-\ $ pénombre portée
 
$4-\ $ ombre portée

Exercice 7

On éclaire un écran $E$ à l'aide d'une source lumineuse étendue puis une boule opaque est placée dans le faisceau lumineux.
 
Représentation de la source lumineuse étendue et du faisceau lumineux ainsi que l'ombre propre, la pénombre propre, l'ombre portée et la pénombre portée de la boule.

 

 
En nous inspirant du schéma précédent, expliquons, schéma à l'appui le phénomène de l'éclipse de Soleil.
 
On parle d'éclipse de soleil lorsque le soleil, la lune et la terre sont alignés dans cet ordre.

 

 
 
Cette position de la lune empêche totalement ou partiellement les faisceaux lumineux du soleil d'atteindre la surface de la terre.
 
$-\ $ Pour un observateur situé sur terre, à l'ombre portée de la lune, le soleil est totalement caché : on parle alors d'éclipse totale.
 
$-\ $ Un individu placé sur terre, à la pénombre portée de la lune, ne voit qu'une partie du soleil : on parle ainsi d'éclipse partielle.

Exercice 8

1) Reproduisons la figure 1 et traçons les faisceaux lumineux, de la source ponctuelle jusqu'à l'écran, puis représentons l'ombre propre et l'ombre portée de la sphère.

 

 
2) Reproduisons la figure 2, puis représentons l'ombre propre de l'objet, son ombre portée, le cône d'ombre et la pénombre portée.

 

 

Exercice 9

Dans le schéma ci-dessous sont représenté le Soleil, la Terre et la Lune
 
Le Soleil et la Lune sont deux sources de lumière.
 
1) Le soleil représente la source primaire et la lune la source secondaire.

 

 
2) Reproduisons en représentant les parties de la terre dans le jour et dans la nuit.

 

 
3) Reproduisons et représentons les parties de la terre dans le jour, dans la nuit et celles dans le clair de lune.

 

 

Auteur: 
Aliou ndiaye

Solution des exercices : Poids d'un corps - relation poids masse - 4e

Classe: 
Quatrième
 

Exercice 1

Complétons ces phrases à trous par les mots ou groupes de mots suivants :
 
intensité ; $g$ ; vertical ; point d'application ; dynamomètre ; altitude; poids ; rectiligne ; proportionnelles ; latitude ; des caractéristiques ; newton ; vectorielle ; $P=mg$ ; le sens ; direction ; vecteur.
 
Dans son voisinage, la terre attire chaque objet ; cette attraction est appelée poids de l'objet.
 
Dans un même lieu, deux objets distincts peuvent être attirés différemment par la terre.
 
On dit que le poids d'un objet possède une  intensité.
 
L'intensité du poids s'exprime en newton et se mesure à l'aide d'un dynamomètre.
 
Les objets sont toujours attirés vers le bas par la terre : ceci correspond au sens du poids.
 
Pendant une chute, une mangue attirée par la terre suit un trajet rectiligne et vertical ; le poids possède alors une direction.
 
L'intensité, le sens et la direction sont des caractéristiques ; l'autre caractéristique est le point d'application.
 
A cause de ces quatre caractéristiques, le poids est une grandeur vectorielle ; il est représenté par un vecteur.
 
L'intensité du poids et la masse sont proportionnelles et sont reliées par la relation $P=mg.$
 
L'intensité de la pesanteur notée $g$ ; elle varie en latitude et en altitude.
 

Exercice 2

Mettons une croix dans la case qui correspond à la bonne réponse :
 
Le poids d'un objet est :
 
$\boxed{\times}\ $ l'attraction terrestre
 
$\boxed{\ }\ $  l'attraction lunaire
 
$\boxed{\ }\ $  l'attraction d'un aimant
 
Le déplacement d'un objet du haut vers le bas correspond :
 
$\boxed{\ }\ $  à la direction du poids
 
$\boxed{\ }\ $  à l'intensité du poids
 
$\boxed{\times}\ $  au sens du poids
 
L'intensité du poids s'exprime en :
 
$\boxed{\ }\ $  kilogramme
 
$\boxed{\times}\ $  newton
 
$\boxed{\ }\ $  mètre
 
L'intensité du poids se mesure avec :
 
$\boxed{\ }\ $  une balance
 
$\boxed{\ }\ $  un rapporteur
 
$\boxed{\times}\ $  un dynamomètre
 
L'intensité du poids et la masse d'un objet sont :
 
$\boxed{\ }\ $  égales
 
$\boxed{\ }\ $  opposées
 
$\boxed{\times}\ $  proportionnelles
 
La relation entre l'intensité du poids $P$ et la masse $m$ d'un objet est :
 
$\boxed{\ }\ \ P=\dfrac{m}{g}$
 
$\boxed{\times}\ \ P=m.g$
 
$\boxed{\ }\ \ P=\dfrac{g}{m}$
 
L'intensité de la pesanteur a pour unité :
 
$\boxed{\times}\ \ N.kg^{-1}$
 
$\boxed{\ }\ \ N.kg$
 
$\boxed{\ }\ \ N^{-1}.kg$
 

Exercice 3

L'intensité du poids d'un objet est $P=750\;N.$
 
1) Donnons les caractéristiques de ce poids.
 
$-\ \ $ Point d'application : le point considéré (point $O$)
 
$-\ \ $ Sens : du haut vers le bas
 
$-\ \ $ Direction : verticale
 
$-\ \ $ Intensité : $||\vec{P}||=P=750\;N$
 
2) Faisons la représentation vectorielle du poids de cet objet à l'échelle de $1\;cm$ pour $150\;N.$

 
 

Exercice 4

Complétons le tableau suivant en calculant la grandeur qui manque dans chaque colonne :
 
On rappelle que : $P=m.g$
 
Et on tire : $m=\dfrac{P}{g}\quad\text{et}\quad g=\dfrac{P}{m}$
$$\begin{array}{|c|c|c|c|c|c|}\hline P&15\;N&19.6\;daN&3.924\;N&2.4\;kN&46.944\;kN\\ \hline m&1.5\;kg&20\;kg&400\;g&240\;kg&4.8\;t\\ \hline g(N.kg^{-1})&10&9.8&9.81&10&9.78\\ \hline\end{array}$$

Exercice 5

Le poids d'un objet $A$ est représenté par un vecteur de longueur $5\;cm$ à l'échelle de $1\;cm$ pour $30\;N.$
 
1) Calculons l'intensité $\|\vec{P}_{_{A}}\|$, du poids de $A.$
 
Comme $1\;cm$ représente $30\;N$ alors, $5\;cm$ vont représenter $5\times 30\;N$
 
Soit : $\boxed{\|\vec{P}_{_{A}}\|=150\;N}$
 
En effet,
$$\begin{array}{rcl} 1\;cm&\longrightarrow&30\;N\\ 5\;cm&\longrightarrow&\|\vec{P}_{_{A}}\|\end{array}$$
Donc, en utilisant la règle de proportionnalité, on obtient :
$$\dfrac{\|\vec{P}_{_{A}}\|}{30\;N}=\dfrac{5\;cm}{1\;cm}\ \Rightarrow\ \|\vec{P}_{_{A}}\|=5\times 30\;N$$
 
2) Calculons la masse $m_{_{A}}$, de $A$
 
On sait que : $\|\vec{P}_{_{A}}\|=m_{_{A}}.g$
 
Ce qui entraîne : $m_{_{A}}=\dfrac{\|\vec{P}_{_{A}}\|}{g}$
 
Or, $g=10\;N.kg^{-1}$ donc, $m_{_{A}}=\dfrac{150}{10}=15$
 
Ainsi, $\boxed{m_{_{A}}=15\;kg}$

Exercice 6

1) Le poids d'un objet $B$ a pour intensité $840\;N.$
 
Déterminons l'échelle utilisée. soit : $1\;cm$ pour $x\;N$
 
Le poids de l'objet $B$ étant représenté par un vecteur de longueur $4.2\;cm$ alors, on peut écrire :
$$\begin{array}{rcl} 4.2\;cm&\longrightarrow&840\;N\\ 1\;cm&\longrightarrow&x\;N\end{array}$$
Ce qui donne : $\dfrac{x}{840}=\dfrac{1}{4.2}$
 
Donc, $x=\dfrac{1\times 840}{4.2}=200$
 
D'où, l'échelle utilisée est :
$$1\;cm\longrightarrow 200\;N$$
2) Un poids d'intensité $2500\;mN$ est représenté par le vecteur ci-dessous.

 

 
Déterminons l'échelle utilisée pour représenter ce poids.
 
En mesurant la longueur de ce vecteur, on trouve : $2.5\;cm$
 
Donc, $2.5\;cm$ vont représenter $2500\;mN$ ; ce qui veut dire que $1\;cm$ représente $\dfrac{2500}{2.5}\;mN.$ Soit : $1000\;mN$
 
Ainsi, l'échelle utilisée pour représenter ce poids est donnée par :
$$1\;cm\longrightarrow 1000\;mN=1\;N$$

Exercice 7

1) Calculons l'intensité du poids d'un objet de masse $m=350\;kg$
 
On a : $P=m\times g$ avec $g=10\;N.kg^{-1}$
 
A.N : $P=350\times 10=3500$
 
D'où, $\boxed{P=3500\;N}$
 
2) Représentons le poids de cet objet.
 
En prenant comme échelle $1\;cm$ pour $1000\;N$, le poids sera alors représenté par un vecteur de longueur $x=\dfrac{3500}{1000}=3.5\;cm$

 

 
 

Exercice 8

$-\ $ En un lieu, l'intensité du poids d'un objet $A$ de masse $6\;kg$ est de $58.74\;N$
 
$-\ $ En ce lieu, un objet $B$ a un poids d'intensité $19.58\;N$
 
Calculons la masse de l'objet $B$
 
On a : $P_{_{B}}=m_{_{B}}\times g$
 
Donc, $m_{_{B}}=\dfrac{P_{_{B}}}{g}\quad(*)$
 
Or, $g$ est une constante qu'on peut déterminer en utilisant les données de l'objet $A.$
 
Ainsi, on a : $P_{_{A}}=m_{_{A}}\times g$
 
Ce qui donne : $g=\dfrac{P_{_{A}}}{m_{_{A}}}\quad(**)$
 
Pour l'objet $B$, on a : $P_{_{B}}=m_{_{B}}\times g$
 
Ce qui entraîne : $m_{_{B}}=\dfrac{P_{_{B}}}{g}$
 
Par suite, en remplaçant dans la relation (*), l'expression de $g$ donnée par la relation (**), on obtient :
$$m_{_{B}}=\dfrac{P_{_{B}}}{\dfrac{P_{_{A}}}{m_{_{A}}}}=\dfrac{P_{_{B}}\times m_{_{A}}}{P_{_{A}}}$$
A.N : $m_{_{B}}=\dfrac{19.58\times 6}{58.74}=2$
 
Ainsi, $\boxed{m_{_{B}}=2\;kg}$
 

Exercice 9

Un astronaute a une masse de $70\;kg$ sur terre.
 
1) Déterminons sa masse $(m_{_{\text{(sur lune)}}})$ sur la lune
 
Comme la masse d'un corps est constante quelque soit l'endroit ou l'espace qu'il se trouve alors,
$$m_{_{(\text{sur lune})}}=m_{_{(\text{sur terre})}}=70\;kg$$
 
2) Calculons l'intensité de son poids sur la lune.
 
On a : $P_{_{(\text{sur lune})}}=m_{_{(\text{sur lune})}}\times g_{_{(\text{sur lune})}}$
 
avec $g_{_{(\text{sur lune})}}=1.6\;N\cdot kg^{-1}$
 
A.N : $P_{_{(\text{sur lune})}}=70\times 1.6=112$
 
D'où, $\boxed{P_{_{(\text{sur lune})}}=112\;N}$
 

Exercice 10

Le poids d'un objet est représenté par le vecteur ci-dessous :

 

 
Calculons son intensité si l'échelle utilisée est de $1\;cm$ pour $150\;N$
 
En mesurant le vecteur, on trouve : $2.5\;cm$ 
 
Or, d'après l'échelle utilisée, $1\;cm$ représente $150\;N.$
 
Par suite, $2.5\;cm$ vont représenter $150\;N\times 2.5=375\;N$
 
D'où, $\boxed{P=375\;N}$
 

Exercice 11 Maitrise de connaissances

Recopions et complétons les phrases suivantes par les mots :
 
$N.Kg^{-1}$, un vecteur, varie, l'origine, $P=m.g$, newton, la Terre, centre de gravité, de haut en bas, verticale, l'attraction.
 
Le poids d'un corps est l'attraction exercée par la Terre sur ce corps.
 
Le poids d'un corps peut être modélisé par un vecteur de direction verticale dont le sens est de haut en bas. Par convention, on place l'origine de ce vecteur au centre de gravité du corps.
 
La relation entre la valeur du poids $P$ d'un corps et sa masse $m$ s'écrit : $P=m.g$
 
L'intensité de la pesanteur $g$ se mesure en $N.Kg^{-1}$ dans le système International et varie avec le lieu.
 

Exercice 12  Vrai ou Faux

Mettons vrai (V) ou faux (F) devant chaque proposition.
 
1) La direction du poids est oblique.$\quad(F)$
 
2) le point d'application du poids d'un corps est le centre de gravité de ce dernier.$\quad(V)$
 
3) la valeur du poids d'un objet se mesure avec une balance.$\quad(F)$
 
4) la relation entre le poids et la masse est $m=\dfrac{P}{m}\quad(F)$
 
5) le sens du poids est du bas vers le haut.$\quad(F)$
 
6) L'ordre de $g$ est de $10\;N.kg^{-1}\quad(V)$

Exercice 13 Utilisation de la bonne unité

Corrigeons les erreurs observées :
 
$-\ $ sur une boite de sucre : "masse nette : $1\;kg$"
 
En effet, l'unité de masse est le kilogramme $(kg)$ et l'unité de poids, le Newton $(N).$
 
Comme une boite de sucre pèse $1\;kg$ alors, au lieu de "poids net" on doit mettre "masse nette".
 
$-\ $ sur une plaque de chocolat : "Masse $125\;g$"
 
$-\ $ sur un véhicule utilitaire : "Poids à vide $1520\;N$"
 
En effet l'unité du poids étant le Newton $(N)$ donc, à la place de $kg$ on mettra $N.$
 

Exercice 14 Relation poids et masse

Un élévateur peut soulever des objets dont le poids ne dépasse pas $5000\;N.$
 
Déterminons la masse $(m)$ qui correspond à cette charge maximale
 
On sait que le poids maximal que l'élévateur peut soulever est : $P=5000\;N$
 
Ce poids va donc correspondre à une charge maximale de masse $m$ telle que :
$$P=m.g$$
Par suite, $m=\dfrac{P}{g}$ avec $g=9.8\;N.kg^{-1}$
 
A.N : $m=\dfrac{5000}{9.8}=510.2$
 
Ainsi, $\boxed{m=510.2\;kg}$
 

Exercice 15 Schématisation

Une boule repose sur un sol horizontal. La valeur de son poids est de $5\;N.$
 
Représentons le poids $\vec{P}$ de la boule en choisissant comme échelle : $1\;cm$ pour $2\;N.$
 
Pour cela, on doit trouver la longueur $x$ du vecteur représentant ce poids.
 
Comme $1\;cm$ représente $2\;N$ alors,  on a :
$$\begin{array}{rcl} 1\;cm&\longrightarrow&2\;N\\x\;cm&\longrightarrow&5\;N\end{array}$$
Ce qui donne : $\dfrac{x}{1}=\dfrac{5}{2}=2.5$
 
Par suite, $x=2.5\;cm$
 
D'où, le poids de la boule sera représenté par un vecteur dirigé vers le bas et de longueur $2.5\;cm.$

 

 

Exercice 16 Distinction poids et masse

Fatou a une masse $m=60\;kg.$
 
1) Calculons son poids $(P_{_{T}})$ sur Terre.
 
On a : $P_{_{T}}=m.g_{_{T}}$ avec $g_{_{T}}=9.8\;N.kg^{-1}$
 
A.N : $P_{_{T}}=60\times 9.8=588$
 
Ainsi, $\boxed{P_{_{T}}=588\;N}$
 
2) Déterminons sa masse $(m_{_{L}})$ sur la Lune
 
La masse étant une grandeur physique constante alors :
$$m_{_{L}}=m$$
D'où, $\boxed{m_{_{L}}=60\;kg}$
 
3) Son poids $(P_{_{L}})$ sur la Lune est donné par :
$$P_{_{L}}=m_{_{L}}.g_{_{L}}$$
avec $g_{_{L}}=1.6\;N.kg^{-1}$
 
A.N : $P_{_{L}}=60\times 1.6=96$
 
Donc, $\boxed{P_{_{L}}=96\;N}$
 
4) Comparons le poids terrestre et le poids lunaire de Fatou.
 
On a : $P_{_{T}}=588\;N\ $ et $\ P_{_{L}}=96\;N$
 
Comme $588>96$ alors, $P_{_{T}}>P_{_{L}}$
 
Ce qui veut dire que le poids terrestre de Fatou est supérieur à son poids lunaire.
 
On peut aussi dire que le poids d'une masse quelconque est plus important sur Terre que sur la Lune.

Exercice 18

Déterminons les caractéristiques du poids $\vec{P}$ de l'objet $A$ représenté ci-dessous

 

 
$-\ $ Point d'application : centre de gravité de l'objet $A$
 
$-\ $ Sens : du haut vers le bas
 
$-\ $ Direction : verticale
 
$-\ $ Intensité : $||\vec{P}||=2.25\;N$
 
En effet, par mesure, on obtient comme échelle : $1\;cm$ pour $0.5\;N$
 
De plus, la mesure du vecteur $\vec{P}$ donne : $4.5\;cm$
 
Donc, on a :
$$\begin{array}{rcl} 1\;cm&\longrightarrow&0.5\;N\\4.5\;cm&\longrightarrow&\|\vec{P}\|\end{array}$$
Par suite, $\dfrac{4.5}{1}=\dfrac{\|\vec{P}\|}{0.5}$
 
Ce qui donne : $\|\vec{P}\|=4.5\times 0.5=2.25$
 
D'où, $\|\vec{P}\|=2.25\;N$

 

Auteur: 
Aliou ndiaye

Solution des exercices : Grandeurs physiques et mesures - 4e

Classe: 
Quatrième
 

Exercice 1

Complétons le tableau suivant :
$$\begin{array}{|c|c|c|c|} \hline \text{Grandeurs}&\text{Nom de l'unité}&\text{Symbole de}&\text{Instrument de}\\ \text{physiques}& &\text{l'unité}&\text{mesure}\\ \hline\text{longueur}&\text{mètre}&m&\text{règle graduée}\\ \hline\text{masse}&\text{kilogramme}&kg&\text{balance}\\ \hline\text{volume}&\text{mètre cube}&m^{3}&\text{burette,}\\&&&\text{éprovette graduée}\\ \hline\text{intensité}&&&\\ \text{du courant}&\text{ampère}&A&\text{ampèremètre}\\ \text{électrique}&&&\\ \hline\text{temps}&\text{seconde}&s&\text{chronomètre}\\ \hline\text{température}&\text{degré Kelvin}&^{\circ}K&\text{thermomètre}\\ \hline\end{array}$$

Exercice 2

1) Complétons le tableau en précisant pour chaque instrument de mesures, la grandeur physique mesurée :
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{balance}&\text{chronomètre}&\text{thermomètre}&\text{sablier}&\text{règle}&\text{ampèremètre}\\ & & & &\text{graduée}&\\ \hline\text{masse}&\text{temps}&\text{température}&\text{intervalle}&\text{longuaur}&\text{intensité du}\\&&&\text{de temps}&&\text{courant électrique}\\ \hline \end{array}$$
2) Indiquons pour chaque instrument de mesure une personne qui a l'habitude de l'utiliser.
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{balance}&\text{chronomètre}&\text{thermomètre}&\text{ruban-mètre}&\text{multimètre}&\text{manomètre}\\ \hline\text{commerçant}&\text{arbitre}&\text{médecin}&\text{maçon}&\text{électricien}&\text{frigoriste}\\ \hline\end{array}$$

Exercice 3

Classons les mots dans un tableau à deux colonnes, une pour les grandeurs physiques et l'autre pour les unités.
$$\begin{array}{|l|c|}\hline\text{Grandeurs physiques}&\text{Unités}\\ \hline\text{distance}&\text{kilomètres}\\ \hline\text{volume}&dm^{3}\\ \hline\text{masse}&kg\\ \hline\text{durée (temps)}&\text{heures}\\ \hline\text{température}&^{\circ}C\\ \hline\end{array}$$

Exercice 4

1) Donnons l'écriture scientifique des nombres suivants :
 
Écrire un nombre en notation scientifique revient à l'écrire sous la forme :
$$a\times 10^{n}$$
avec : $\ 1\leq a<10\quad\text{ ou}\quad -10<a\leq -1\ $ et $\ n$ un entier relatif.
 
a) On a : $178\;m=178.0\;m$
 
On peut alors déplacer $2$ fois la virgule vers la gauche jusqu'au dernier chiffre significatif.
 
Or, déplacer $n$ fois la virgule à gauche, se compense en multipliant par $10^{n}$
 
Donc, $178.0\;m=1.78\times 10^{2}\;m$
 
b) Soit : $15386\;kg=15386.0\;kg$
 
En déplaçant $4$ fois la virgule vers la gauche, on arrive au dernier chiffre significatif.
 
Par suite, $15386\;kg=1.5386\times 10^{4}\;kg$
 
c)  On a : $6000\;W=6\times 1000=6\times 10^{3}\;W$
 
d) Soit le nombre $0.000876$
 
En déplaçant $4$ fois la virgule vers la droite, on dépasse le premier chiffre significatif.
 
Comme déplacer $n$ fois la virgule vers la droite, se compense en multipliant par $10^{-n}$ alors, $$0.000876=8.76\times 10^{-4}$$
2) Donnons l'ordre de grandeur des valeurs numériques suivantes :
 
Par définition, l'ordre de grandeur d'une valeur numérique est la puissance de dix entière la plus proche de cette valeur. 
 
a) Soit le nombre $6370$
 
En écriture scientifique, on a : $6370=6.370\times 10^{3}$
 
On constate que le premier chiffre significatif $(6)$ est strictement supérieur à $5$ donc, l'ordre de grandeur du nombre $6370=6.370\times 10^{3}$ est égal à la puissance de $10$ suivante ; c'est-à-dire $10^{3+1}=10^{4}.$
 
Ainsi, $6370\sim 10^{4}$
 
b) Soit le nombre $1.035\times 10^{3}$ alors, son premier chiffre significatif $(1)$ est strictement inférieur à $5.$
 
Par conséquent, l'ordre de grandeur de ce nombre est la puissance de $10$ associée $(10^{3}).$
 
D'où, $1.035\times 10^{3}\sim 10^{3}$
 
c) Pour le nombre $2.876\times 10 ^{2}$, on constate que son premier significatif $(2)$ est strictement inférieur à $5.$
 
Donc, son ordre de grandeur est la puissance de $10$ associée ; c'est-à-dire $10^{2}.$
 
Par suite, $2.876\times 10^{2}\sim 10^{2}$
 
d) Comme $9>5$ alors l'ordre de grandeur du nombre $9.554\cdot 10^{-3}$ est égal à la puissance de $10$ suivante ; à savoir $10^{-3+1}=10^{-2}.$
 
Ainsi, $9.554\times 10^{-3}\sim 10^{-2}$
 
3) Donner les chiffres significatifs des nombres suivants :
 
a) $0.0041$
 
On a deux chiffres significatifs : $4\ $ et $\ 1$
 
b) $0.2075$
 
On obtient quatre chiffres significatifs : $2\;,\ 0\;,\ 7\ $ et $\ 5$ dans cet ordre.
 
c) Pour le nombre $6.0532890$, tous les chiffres sont significatifs
 
d) Pour le nombre $0.0000010$, on obtient deux chiffres significatifs : $1\ $ et $\ 0$ (c'est le $0$ qui se trouve le plus à droite).

Exercice 5

1) Convertissons les masses suivantes :
 
a) $1\;kg=1\,000\;g=1\times 10^{3}\;g$
 
b) $1\;g=0.001\;kg=1\times 10^{-3}\;kg$
 
c) $0.9\;hg\ $ en $\ mg$ 
 
On a : $1\;hg=1\times 10^{5}\;mg$ donc, $0.9\;hg=0.9\times 10^{5}\;mg=9\times 10^{4}\;mg$
 
d) $1.8\;kg\ $ en $\ g$
 
Comme $1\;kg=1\times 10^{3}\;g$ alors, $1.8\;kg=1.8\times 10^{3}\;g$
 
2) Convertissons les volumes suivants :
 
a) $25000\;mL\ $ en $\ hL$
 
On sait que : $1\;mL=1\times 10^{-5}\;hL$
 
Donc, $25000\;mL=25000\times 10^{-5}\;hL=0.25\;hL$
 
b) $0.25\;hL\ $ en $\ L$ 
 
On a : $1\;hL=1\times 10^{2}\;L$
 
Par suite, $0.25\;hL=0.25\times 10^{2}\;L=25\;L$
 
c) $87\;L\ $ en $\ dL$
 
Comme $1\;L=1\times 10^{1}\;dL$ alors, $87\;L=87\times 10^{1}\;dL=870\;dL$
 
d) $0.03\;L\text{ en }mL$
 
Soit : $1\;L=1\times 10^{-3}\;mL$
 
Alors, $0.03\;L=0.03\times 10^{-3}\;mL=30\;mL$
 
e) $1250\;cm^{3}\ $ en $\ dm^{3}$
 
On a : $1\;cm^{3}=1\times 10^{-3}\;dm^{3}$
 
Donc, $1250\;cm^{3}=1250\times 10^{-3}\;dm^{3}=1.25\;dm^{3}$
 
f) $1.5\;dm^{3}\ $ en $\ m^{3}$ 
 
On sait que : $1\;dm^{3}=1\times 10^{-3}\;m^{3}$
 
Par suite, $1.5\;dm^{3}=1.5\times 10^{-3}\;m^{3}$
 
g) $1.5\;dm^{3}\ $ en $\ mL$ 
 
Comme $1\;dm^{3}=1\times 10^{3}\;mL$ alors, $1.5\;dm^{3}=1.5\times 10^{3}\;mL$
 
h) $125\;mL\text{ en }dm^{3}.$
 
On a : $1\;mL=1\times 10^{-3}\;dm^{3}$
 
Ainsi, $125\;mL=125\times 10^{-3}\;dm^{3}=1.25\cdot 10^{-1}\;dm^{3}$

Exercice 6

1) Écrivons à l'aide d'une puissance de $10$, les nombres suivants :
 
a) $0.000000000001=10^{-12}$
 
b) $100000000=10^{8}$
 
c) $1=10^{0}$
 
d) $10000=10^{4}$
 
2) Écrivons à l'aide d'une puissance de $10$, les nombres suivants :
 
a) $\text{un milliard}=1\,000\,000\,000=10^{9}$
 
b) $\text{un millième}=\dfrac{1}{1\,000}=0.001=10^{-3}$
 
c) $\text{cent mille}=100\,000=10^{5}$
 
d) $\text{un millionième}=\dfrac{1}{1\,000\,000}=0.000001=10^{-6}$
 
3) Exprimons sous la forme d'une puissance de $10$, les nombres suivants :
 
On utilise les propriétés suivantes :
$$a^{n}\times a^{m}=a^{(n+m)}\quad\text{et}\quad a\times 10^{n}+b\times 10^{n}=(a+b)\times 10^{n}$$
a) $10^{5}\times 10^{7}=10^{5+7}=10^{12}$
 
b) $10^{-11}\times 10^{3}\times 10^{2}=10^{-11+3+2}=10^{-6}$
 
c) On a : $3.1\times 10^{5}=310\times 10^{3}$ donc,
 
$\begin{array}{rcl} 3.1\times 10^{5}+4.8\times 10^{3}&=&310\times 10^{3}+4.8\times 10^{3}\\ \\&=&(310+4.8)\times 10^{3}\\ \\&=&314.8\times 10^{3}\end{array}$
 
En écrivant le nombre $314.8$ en notation scientifique, on obtient :
$$314.8=3.148\times 10^{2}$$
Par suite,
 
$\begin{array}{rcl} 314.8\times 10^{3}&=&3.148\times 10^{2}\times 10^{3}\\ \\&=&3.148\times 10^{2+3}\\ \\&=&3.148\times 10^{5}\end{array}$
 
D'où, $3.1\times 10^{5}+4.8\times 10^{3}=3.148\times 10^{5}$

Exercice 7

1) Parmi les nombres suivants, $5.23\times 10^{12}$ et d) $-1.47\times 10^{6}$ sont écrits en notation scientifique
 
$0.251\times 10^{3}$ n'est pas écrit en notation scientifique car $0.251<1$
 
$72.43\times 10^{-8}$ n'est pas écrit en notation scientifique car $72.43>1$
 
2) Écrivons les nombres suivants en notation scientifique
 
a) $7283=7.283\times 10^{3}$
 
b) $12.47=1.247\times 10^{1}$
 
c) $0.67\times 10^{2}=6.7\times 10^{1}$
 
d) $0.0058=5.8\times 10^{-3}$

Exercice 8

Calculons et donnons les résultats sous la forme d'une écriture scientifique :
 
a)
 
$\begin{array}{rcl} 150\times 10^{3}\times 8\times 10^{5}&=&150\times 8\times 10^{3}\times 10^{5}\\ \\&=&1200\times 10^{3+5}\\ \\&=&1200\times 10^{8}\\ \\&=&1.200\times 10^{3}\times 10^{8}\\ \\&=&1.2\times 10^{3+8}\\ \\&=&1.2\times 10^{11}\end{array}$
 
Donc, $\boxed{150\times 10^{3}\times 8\times 10^{5}=1.2\times 10^{11}}$
 
b)
 
$\begin{array}{rcl} 2\times 10^{9}\times 7\times 10^{6}&=&2\times 7\times 10^{9}\times 10^{6}\\ \\&=&14\times 10^{9+6}\\ \\&=&14\times 10^{15}\\ \\&=&1.4\times 10^{1}\times 10^{15}\\ \\&=&1.4\times 10^{1+15}\\ \\&=&1.4\times 10^{16}\end{array}$
 
Ainsi, $\boxed{2\times 10^{9}\times 7\times 10^{6}=1.4\times 10^{16}}$
 
c)
 
$\begin{array}{rcl} 2\times 10^{3}\times 5\times 10^{-5}&=&2\times 5\times 10^{3}\times 10^{-5}\\ \\&=&10\times 10^{3-5}\\ \\&=&10^{1}\times 10^{-2}\\ \\&=&10^{-1}\end{array}$
 
D'où, $\boxed{2\times 10^{3}\times 5\times 10^{-5}=10^{-1}}$
 
d)
 
$\begin{array}{rcl} 3\times 10^{2}\times 1.2\times 10^{-5}&=&3\times 1.2\times 10^{2}\times 10^{-5}\\ \\&=&3.6\times 10^{2-5}\\ \\&=&3.6\times 10^{-3}\end{array}$
 
Donc, $\boxed{3\times 10^{2}\times 1.2\times 10^{-5}=3.6\times 10^{-3}}$

Exercice 9

Notre planète est entourée d'une couche d'air dont la plus grande partie est répartie sur une épaisseur d'une dizaine de kilomètres.
 
On appelle pression atmosphérique la pression qu'exerce cette couche d'air sur les corps à la surface de la Terre.
 
Le symbole de la pression est $P.$
 
La pression atmosphérique est une donnée précieuse pour la météorologie car les mouvements des masses d'air en altitude sont responsables de l'évolution du climat.
 
La mesure de la pression atmosphérique est donc nécessaire pour prévoir les conditions climatiques. L'unité légale de la pression est le pascal $($symbole : $Pa).$
 
La pression atmosphérique est mesurée par un appareil de mesure : le baromètre. Certains baromètres sont gradués en hectopascals $($symbole : $hPa)$ ou en millibars $($symbole : $mbar).$
 
D'autres baromètres sont gradués en hauteur de colonne de mercure $($symbole : $mm\,Hg).$
 
1) L'instrument de mesure cité dans ce texte est le baromètre
 
2) Le baromètre mesure la pression atmosphérique
 
3) Le symbole de la pression $P$
 
4) L'unité de pression dans le système international est le Pascal. Son symbole est : $Pa$
 
5) Les autres unités de pression citées dans le texte sont :
 
$-\ $ hectopascals : $hPa$
 
$-\ $ millibars : $mbar$
 
$-\ $ millimètre de mercure : $mm\,Hg$
 
6) Convertissons un hectopascal en pascal.
 
On a : $1\,hPa=100\,Pa$
 
7) A part les laboratoires de météorologie, on trouve les appareils qui permettent de mesurer la pression dans les laboratoires de physique, de chimie, dans les stations de gonflage, dans les usines de transformation des aliments, dans les usines de montage par injection.
 
Ces appareils de mesure de la pression atmosphérique sont donc utilisés par les physiciens, les chimistes, les architectes, les agents des stations de gonflage et certains ingénieurs et techniciens d'usines de transformations ou de montage.

Exercice 10

Complétons la phrase ci-dessous
 
L'écriture scientifique d'un nombre est donnée par le produit d'un nombre décimal compris entre $1\ $ et $\ 10$ par une puissance entière de $10.$

Exercice 11 Conversion d'unités

Effectuons des conversions suivantes
 
1) $3\;km=3\times 10^{2}\;dam=3\times 10^{3}\;m=3\times 10^{6}\;mm$
 
2) $1.5\;dm=1.5\times 10^{-1}\;m=1.5\times 10^{2}\;mm$
 
3) $62\;g=62\times 10^{3}\;mg=62\times 10^{-3}\;kg=62\times 10^{-6}\;t$
 
4) $4.2\;dm^{3}=4.2\times 10^{3}\;cm^{3}=4.2\times 10^{3}\;ml$
 
5) $0.9\;hl=9\times 10^{-2}\;m^{3}=90\;l=9\times 10^{4}\;cm^{3}$
 
6) $1.3\cdot 10^{-6}km^{2}=1.3\;m^{2}=1.3\times 10^{2}\;dm^{2}=1.3\times 10^{6}\;mm^{2}$

Exercice 13 Chiffres significatifs et notation scientifique

Les données ci-dessous correspondent à des résultats de mesure de longueur exprimés en mètre.
 
Pour chaque mesure, le nombre de chiffres significatifs pour chaque mesure et exprimons ces données en notation scientifique.
$$\begin{array}{|c|c|c|c|c|c|c|} \hline&A&B&C&D&E&F\\ \hline\text{résultats}&&&&&&\\\text{de}&5.43&58.0&1200&0.0005&4804.02&20.300\\\text{mesure}&&&&&&\\\hline\text{nombre de}&&&&&&\\\text{chiffres}&3&3&4&1&6&5\\\text{significatifs}&&&&&&\\\hline\text{expression}&&&&&&\\\text{en notation}&5.43\cdot 10^{0}&5.80\cdot 10^{1}&1.200\cdot 10^{3}&5\cdot 10^{-4}&4.80402\cdot 10^{3}&2.0300\cdot 10^{1}\\\text{scientifique}&&&&&&\\ \hline\end{array}$$

Exercice 14 Se servir du double-décimètre

Une longueur est mesurée avec une règle graduée en $cm.$
 
1) L'écriture correcte de la valeur mesurée est la valeur affichée en b) : $13.0\;cm$
 
2) Donnons une explication au rejet de chacune des autres valeurs.
 
Comme le double décimètre est divisé en centimètres et en millimètres alors, il ne permet pas de mesurer une longueur au $\dfrac{1}{10}$ ou au $\dfrac{1}{100}$ de millimètre $(mm)$ près.
 
D'où, le rejet des valeurs affichées en a) et c).
 
De plus, la précision du double décimètre étant de l'ordre de $1\;mm$ près donc, la valeur en a), donnée à $1\;cm$ près ; soit $10\;mm$ près peut être entachée d'erreurs. D'où, son rejet.

Exercice 15 Précision d'une mesure

Les écritures du résultat de la mesure d'une longueur sont notées ci-dessous.
 
1) Entourons la lettre qui correspond à la mesure la plus précise
 
a) $15.2\;cm$
 
b) $0.152\;m$
 
c) $152\;mm$
 
$\boxed{\text{d) }152.0\;mm}$
 
e) $152\cdot 10^{-3} m$
 
2) Justification de ce choix.
 
En effet, on constate que ce nombre comporte $4$ chiffres significatifs tandis que les autres n'en comptent que $3.$ Donc, $152.0\;mm$ est la mesure la plus précise (trois valeurs sont connues avec certitude alors qu'avec les autres mesures on ne connait que deux valeurs).

Exercice 16 Précision d'un calcul à partir de valeurs mesurées

Les mesures des dimensions de deux champs rectangulaires ont donné les résultats suivants :
 
$\centerdot\ $ Champ 1 : $L_{1}=121.9\;m\ $ et $\ \ell_{1}=65.0\;m$
 
$\centerdot\ $ Champ 2 : $L_{2}=1.46\;m\ $ et $\ \ell_{2}=0.78\;m$
 
1) Calculons les aires $A_{1}\ $ et $\ A_{2}$ des surfaces correspondantes en respectant le nombre de chiffres significatifs.
 
En effet, dans une multiplication le résultat doit avoir le même nombre de chiffres significatifs que le facteur avec le moins de chiffres significatifs.
 
Ainsi, pour le champ 1 on a :
 
$\begin{array}{rcl} A_{1}&=&L_{1}\times\ell_{1}\\ \\&=&121.9\times 65.0\\ \\&=&7\,923.5\end{array}$
 
Comme le facteur $2$, avec $3$ chiffres significatifs, est le facteur comportant le moins de chiffres significatifs alors,
$$\boxed{A_{1}=7.92\times 10^{3}\;m^{2}}$$
pour le champ 2, on a :
 
$\begin{array}{rcl} A_{2}&=&L_{2}\times\ell_{2}\\ \\&=&1.46\times 0.78\\ \\&=&1.1388\end{array}$
 
On constate que le premier facteur compte $3$ chiffres significatifs et que le deuxième facteur en compte $2$ donc, le résultat sera donné avec $2$ chiffres significatifs.
 
Ainsi, en arrondissant au dixième on obtient :
$$\boxed{A_{2}=1.1\;m^{2}}$$
2) Calculons les périmètres correspondants.
 
Il faut noter que dans une addition le résultat doit avoir le même nombre de chiffres après la virgule que le terme de l'addition qui en a le moins.
 
Donc, pour le champ 1 on obtient :
 
$\begin{array}{rcl} P_{1}&=&(L_{1}+\ell_{1})+(L_{1}+\ell_{1})\\ \\&=&(121.9+65.0)+(121.9+65.0)\\ \\&=&186.9+186.9\\ \\&=&373.8\end{array}$
 
Ainsi, $$\boxed{P_{1}=373.8\;m}$$
pour le champ 2 on a :
 
$\begin{array}{rcl} P_{2}&=&(L_{2}+\ell_{2})+(L_{2}+\ell_{2})\\ \\&=&(1.46+0.78)+(1.46+0.78)\\ \\&=&2.24+2.24\\ \\&=&4.48\end{array}$
 
D'où, $$\boxed{P_{2}=4.48\;m}$$

Exercice 17 Disque circulaire

Le périmètre d'un disque circulaire de rayon $R$ est donné par $C=2\pi R$ et l'aire de sa surface a pour l'expression $A=\pi R^{2}.$
 
Un disque circulaire à un diamètre $D=20.0\;cm$
 
1) Déterminons son périmètre.
 
Soit : $C=2\pi R$ or, $\ R=\dfrac{D}{2}$
 
Donc, $C=2\pi\times\dfrac{D}{2}=\pi\times D$
 
A.N : $C=3.14\times 20.0=62.8$
 
D'où, $$\boxed{C=62.8\;cm}$$
2) Calculons l'aire de sa surface.
 
On a :$A=\pi R^{2}$ or, $\ R=\dfrac{D}{2}$
 
Donc, $A=\pi\times\dfrac{D^{2}}{4}$
 
A.N : $A=3.14\times\dfrac{(20.0)^{2}}{4}=314$
 
D'où, $$\boxed{A=314\;cm^{2}}$$
Remarque : Les résultats sont conformes avec les données car, on a $3$ chiffres significatifs.

Exercice 18 Détermination de volume

1) Indiquons la valeur de chaque volume $($en $mL)$ mesuré ci-dessous.

 

 
2) Représentons dans chaque cas le volume indiqué à l'aide d'un trait horizontal.

 
 

Auteur: 
Aliou ndiaye

Série d'exercices : Énergie potentielle - Énergie mécanique - 1er s

Classe: 
Première
 

Exercice 1

Un chariot de montagne russe voyage du point $A$ jusqu'au point $D.$ 
 
Le chariot a une masse de $1000.0\,kg$ et une vitesse de $1.80\,m/s$ au point $A.$
 
 
1) Quelle est l'énergie mécanique (énergie totale) du chariot au point $A$ ?
 
2) Quelle est la vitesse du chariot au point $B$ ?
 
3) Quelle est l'énergie potentielle et l'énergie cinétique du chariot au point $C$ ?
 
4) Quelle est la vitesse du chariot au point $D$ ?

Exercice 2

Paul, debout sur un pont, lance verticalement vers le haut une pierre de masse $m=70\,g.$
 
Celle-ci s'élève jusqu'à une hauteur de $10\,m$ au-dessus du point de lancement puis redescend et tombe dans l'eau.
 
La surface de l'eau est située $2.0\,m$ plus bas que le point de lancement de la pierre.
 
1. Calculer :
 
$-\ $ l'énergie potentielle de pesanteur de la pierre dans sa position la plus haute
 
$-\ $ l'énergie potentielle de pesanteur de la pierre dans sa position la plus basse
 
$-\ $ la variation d'énergie potentielle de la pierre
 
Si l'on choisit comme niveau de référence (origine de l'axe $Oz$ dirigé vers le haut)
 
1.1 Le niveau du point de lancement de la pierre
 
1.2 Le niveau de la surface de l'eau.
 
2. Exprimer l'énergie potentielle de pesanteur de la pierre lorsqu'elle est située à une altitude $z$ quelconque par rapport au point de lancement dans les deux cas précédents

Exercice 3

Un skieur à l'épreuve du kilomètre lancé $(KL)$, en recherche de vitesse sur une piste plane, bien damée et inclinée d'un angle $\alpha=26.0^{\circ}$ par rapport à l'horizontale, part du point $A$ et atteint une vitesse de $182\,km\cdot h^{-1}$ $(=50.5\,m\cdot s^{-1})$ au bout d'un $km$ de piste, au point $B.$
 
La masse du skieur et de son équipement est de $115\,kg.$
 
 
1) Donner l'expression littérale de l'énergie potentielle du skieur en $A.$
 
Faire l'application numérique correspondante en prenant comme origine des énergies potentielles le point $B.$
 
2) Donner l'expression littérale de l'énergie cinétique du skieur en $B.$ 
 
Faire l'application numérique correspondante.
 
3) Nommer les forces appliquées au système {skieur$+$équipement} et les représenter sur un schéma.
 
4) Donner l'expression du travail de chacune de ces forces.
 
5) Donner la relation liant la variation d'énergie cinétique du système et le travail des différentes forces.
 
6) Si le skieur glisse sans frottement. 
 
Quelle serait alors sa vitesse au point $B$ ?
 
7) En fait les frottements ne sont pas négligeables lors d'une telle descente ; déterminer la valeur de ces frottements.

Exercice 4

Dans un parc d'attractions, un wagonnet de masse $m=65\,kg$ se déplace sur des rails dont le profil est donné sur le schéma ci-dessous :
 
Les hauteurs des différents points $A$, $B$, $C$, $D$ et $E$ sont repérées par rapport au sol et ont pour valeurs :
 
$h_{A}=20\,m\quad h_{B}=10\,m\quad h_{C}=15\,m\quad h_{D}=5\,m\quad h_{E}=18\,m$
 
Calculer la variation d'énergie potentielle de pesanteur du wagonnet passant :
 
1) de $A$ à $B$ 
 
2) de $B$ à $C$ 
 
3) de $A$ à $D$ 
 
4) de $A$ à $E$
 
 

Exercice 5

Une piste est constituée par un plan incliné $AB$ de longueur $l=2r$ d'un  angle $\alpha=30^{\circ}$ sur l'horizontale et se raccordant tangentiellement à une portion $BC$ circulaire de centre $O$ et de rayon $r=OB=OC=50\,cm$
 
Un solide $(S)$ ponctuel de masse $m=50\,g$ est suspendu en $C$ au fil $OC$ accroché en $O.$ Un autre solide ponctuel $(S')$ de masse $m'=60\,g$ est lâché sans vitesse initiale au point $A$ et glisse sans frottement le long de la piste. 
 
Au point $C$ il heurte de plein fouet le solide $(S).$ 
 
Prendre $g=9.8\,N\cdot Kg^{-1}$ et $\theta=60^{\circ}$
 
1. Le point $C$ étant considéré comme position de référence, exprimer l'énergie potentielle de pesanteur du solide $(S')$ au point $A$ en fonction de $m'$, $g$, $r$, $\alpha$ et $\theta$ et au point $B$ en fonction $m'$, $g$, $r$ et $\theta$
 
2.1 Calculer l'énergie mécanique totale du solide $(S')$ au point $A.$
 
2.2 Calculer la vitesse du solide $(S')$ au point $B$ et la vitesse qu'il a acquise juste avant le choc au point $C$ en supposant que les forces de frottement sont négligeables sur toute la piste
 
3. Le pendule constitué du solide $(S)$ et le fil s'écarte d'un angle $\beta$ par rapport à la position verticale d'équilibre stable du pendule avant le choc.
 
3.1 Exprimer l'énergie potentielle de pesanteur du solide $(S)$ en fonction de $m$, $g$, $r$ et $\beta$ ; la position verticale étant prise pour position de référence.
 
3.2 Calculer l'énergie mécanique du solide $(S)$ à son départ du point $C$ sachant qu'il acquiert une vitesse $v=3.4\,m\cdot s^{-1}$ juste après le choc.
 
3.3 Calculer le moment d'inertie $J$ du solide $(S)$ par rapport l'axe passant par le point $O'$ et l'écart maximal $\beta_{max}$ atteint par le solide $(S)$ en supposant négligeable la résistance de l'air.
 

 

Exercice 6

Un solide $(S)$ de masse $m=500\,g$ assimilable à un point matériel est lancé à partir d'un point $A$ sur un plan incliné d'un angle $\alpha_{0}=30^{\circ}$ par rapport à l'horizontal avec une vitesse $V_{A}=12\,m/s.$ 
 
La réaction d'intensité supposée constante exercée par le plan sur $(S)$ fait un angle $\alpha_{1}=30^{\circ}$ avec la normale au plan. 
 
La composante de la réaction parallèle au plan incliné a un sens opposé au vecteur vitesse de $\overrightarrow{V}$ de $(S).$
 
1.1 Représenter les forces qui s'exercent sur $(S).$
 
1.2 Calculer les travaux de toutes ces forces au cours du déplacement $AB=\ell=1\,m.$ 
 
On donne $R=0.4\,N$ et $g=10\,N/kg.$
 
1.3 Déterminer la vitesse $V_{B}$ de $(S)$ au point $B.$
 
2. Calculer la variation de l'énergie mécanique de $(S)$ entre les points $A$ et $B.$
 
Dans ce qui suit, la résistance de l'air et les frottements sont supposés nuls. 
 
Le solide $(S)$ continue son mouvement sur $(BC)$ horizontal ; $(CO)$ incliné d'un angle $\delta=40^{\circ}$ par rapport à l'horizontal et $(OD)$ incliné d'un angle $\beta=30^{\circ}$ par rapport à l'horizontal. 
 
En $O$, $(S)$ heurte un solide ponctuel $(S')$ de masse $m'=200\,g$ accroché à l'extrémité d'un fil de longueur $\ell'=10\,cm$ et de masse négligeable ; il s'écarte d'un angle $\theta_{0}$ par rapport à la verticale.
 
3. On prend comme position de référence le point $O$ d'altitude zéro.
 
3.1 Calculer les énergies potentielles de $(S)$ aux points $C$ et $D.$ 
 
$OH=OK=10\,cm.$
 
3.2 Lorsque le solide $(S)$ est sur la partie $(OD)$ de longueur $x\in[0\;;\ 0.1\,m]$, déterminer l'énergie potentielle de $(S)$ en un point de $[OD]$ en fonction de $x.$
 
3.3 Le solide $(S)$ rebrousse chemin en $D.$ 
 
Déterminer l'altitude maximale $Z_{max}$ atteinte sur $[OC]$ par $(S).$
 
4.1 Calculer le moment d'inertie de $(S')$ par rapport à l'axe $(\Delta).$
 
4.2 Exprimer l'énergie potentielle de $(S')$ en fonction de $m'$, $g$, $\ell$ et $\theta_{0}.$
 
4.3 Le solide $(S')$ part de sa position $\theta_{0}$, passe par sa position verticale puis remonte.
 
4.3.1 Déterminer sa vitesse angulaire au passage par sa position verticale avec $\theta_{0}=60^{\circ}.$
 
4.3.2 De quel angle $\theta_{max}$ remonte-t-il ?
 
5. On suppose que $(S)$ et $(S')$ ne se rencontrent plus. 
 
Décrire qualitativement les mouvements ultérieurs de $(S)$ et $(S').$
 
 

Exercice 7

On néglige tous frottements. 
 
Une bille de masse $m$ lancée du point $A$ à la vitesse $v_{A}$ se déplace sur un plan incliné vers le point $D.$ 
 
L'origine de l'énergie potentielle de pesanteur est le point le plus bas $A.$
 
Données : 
 
$m=1.0\,kg\ ;\ OB=0.50\,m\ ;\ AB=2.0\,m\ ;\ \alpha=20^{\circ}\ ;\ \beta=60^{\circ}\ ;\ v_{A}=18\,km/h\text{ et }g=9.8\,N/kg.$
 
1) Calculer les altitudes de $B$, $C$ et $D.$
 
2) Calculer l'énergie mécanique en $A.$
 
3) Calculer les vitesses en $C$ et en $D$ en $km/h.$
 
4) la vitesse initiale $v_{A}$ est divisée par deux, calculer :
 
5) L'énergie mécanique, les vitesses en $C$ et en $D.$
 
 

Exercice 8 

On considère le système mécanique représenté ci-dessous est formé par un parcours $ABC$ et un solide de masse $m=20.0\,g$, assimilable à un point matériel.
 
La partie $AB$ est rectiligne confondue avec le plan horizontal $(\Pi).$
 
La partie $BC$ est une boucle circulaire de rayon $r.$ 
 
On repère le solide dans cette boucle par l'abscisse angulaire $\theta=BOM$
 
 
Les frottements sont négligeables sur tout le parcours $ABC.$ 
 
On prend l'état de référence pour l'énergie potentielle de pesanteur le plan horizontal $(\Pi)$ et l'axe $Oz$ orienté vers le haut.
 
On donne $g=10\,N/kg$
 
1) Exprimer l'énergie potentielle de pesanteur du solide en en fonction de $m$, $g$, et $z$ l'altitude du solide mesurée à partir de l'état de référence choisi.
 
2) Déduire l'énergie potentielle de pesanteur au point $M$ en fonction de $m$, $g$, $r$, et $\alpha$
 
3) Pour quelle position l'énergie potentielle de pesanteur est maximale ? 
 
Justifier votre réponse.
 
4) Trouver l'expression de l'énergie mécanique du solide aux points suivants : $A$, $B$ et $C$, sachant que le solide arrive au point $C$ avec une vitesse $v_{C}.$
 
5) Montrer que le solide parcours le périmètre du boucle, on doit avoir $EC(A)>2mgr.$
 
6) On donne $r=1.5\,m$, calculer la valeur de la vitesse initiale $v_{A}$ pour que le solide arrête au point $C$

Exercice 9

 
Une barre $AB$ homogène de longueur $L=1\,m$, est mobile autour d'un axe horizontal passant par le point $A$ de son extrémité. 
 
Son moment d'inertie par rapport à cet axe est $J\Delta=1/3\,m\cdot L^{2}.$
 
On écarte la barre de sa position d'équilibre stable d'un angle $\alpha=60^{\circ}$ et on le lance, à l'instant $t=0$ avec une
vitesse angulaire $w_{0}=2\,rad/s$
 
Les frottements sont négligeables. 
 
On prend l'état de référence pour l'énergie potentielle de pesanteur le plan horizontal qui passe par $O'$ et l'axe $Oz$ orienté vers le haut.
 
On donne $g=10\,N/kg$
 
1) Calculer la vitesse linéaire $v_{B}$ du point $B$ à l'instant $t=0$
 
2) Trouver l'expression de la variation de l'énergie cinétique entre la position initiale et la position de la barre d'abscisse angulaire $\theta=OAB$ en fonction de $L$, $m$, $g$, $\theta_{0}$ et $\theta$
 
3) Montrer que l'expression de la vitesse angulaire $w$ lorsque la barre passe par la position d'abscisse angulaire $\theta$ est donnée par la relation suivante :
$$w=\sqrt{w_{0}^{2}+\dfrac{3g\left(\cos\theta-\cos\theta_{0}\right)}{L}}$$
 
4) Calculer la vitesse linéaire $v_{B}$ lorsque la barre passe par sa position d'équilibre stable

Exercice 10

Un solide de masse $m_{1}=100\,g$ peut coulisser le long d'un plan inclinée $\alpha=30^{\circ}$ par à rapport à l'horizontal
 
Le solide $S$ est relié à un ressort de constante de raideur $100\,N/m$ dont l'autre extrémité est fixe (voir figure)
 
La position $O$, à l'équilibre, de l'extrémité $M$ du ressort est prise comme origine $(O\;,\ \vec{i})$ d'un repère orienté comme le montre la figure
 
 
1) Donner l'expression littérale et calculer potentielle élastique $E_{pe}$ du système en équilibre en fonction de l'allongement $\Delta Δ_{l0}$ du ressort.
 
Donnée : $g=10\,N/kg$
 
2) Un manipulateur saisit le solide $S$ et le tire vers de telle sorte que l'abscisse de $M$ soit égale $X_{M}=-a=-3\,cm$
 
Donner l'expression littérale et calculer l'énergie potentielle élastique du système
 
3) Donner l'expression littérale et calculer l'énergie potentielle de pesanteur du solide en adoptant la position d'équilibre initiale comme état de référence
 
4) Le manipulateur lâche le solide $S$ qui effectue alors des oscillations le long du plan incliné d'amplitude $a$ ; les frottements sont négligeables
 
Donner l'expression en fonction de $x$ de l'énergie-potentielle élastique $E_{pe}$ et de l'énergie potentielle de pesanteur
 
En déduire l'expression de l'énergie cinétique $E_{C}$
 
Calculer la vitesse du solide lorsque $x=2\,cm$
 
5) Représenter graphiquement en fonction de $x$, $E_{PP}$, $E_{Pe}$ et $E_{C}$
 
Mettre en évidence l'expression de la somme $E_{M}=E_{PP}+E_{Pe}+E_{C}$

Exercice 11 Énergie

Un solide de masse $m=200\,g$ se déplace dans une glissière constituée d'une partie rectiligne $BC$ et d'une partie circulaire $BD$ de centre $O$ et de rayon. 
 
On néglige des frottements. 
 
$G=10\,N/kg.$ 
 
L'origine des altitudes est le point $B$ et celle des énergies potentielles est le plan horizontal contenant $B$ (voir figure 1)
 
 
Le solide part du point $C$ avec une vitesse initiale de $1.6\,m/s$
 
1) Représenter en $C$ et en $M$ les forces appliquées au solide
 
2) Calculer les altitudes $Z_{c}$ et $Z_{e}$ des points $C$ et $E$ ; en déduire l'énergie potentielle du solide lorsqu'il se trouve en chacun de ces points. 
 
On donne $CB=5\,m\ ;\ \alpha=20^{\circ}\ ;\ R=1\,m$
 
3) Calculer le travail du poids lorsque le solide passe de $C$ à $B.$
 
En déduire l'énergie cinétique du solide au point $B$
 
4) Calculer l'énergie mécanique du solide en $B$
 
5) Donner l'expression de la vitesse $V_{M}$ du solide du point $M$ en fonction de $V_{E}$, $m$, $g$, $r$ et $\theta$

AN : 

calculer $V_{m}$ pour $\theta=\dfrac{\pi}{2}$
 
6) Le solide pourra-t-il atteindre le point $D$ ?
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 

Auteur: 
Sidy Mouhamed Ndiaye

Solution des exercices : Les hydrocarbures insaturés : Alcènes et Alcynes - 1er s

Classe: 
Première
 

Exercice 1

A. Nom des composés insaturés suivants :
 
1) $CH_{3}-CH_{2}-CH=CH-CH_{3}$ Pent$-2-$ène
 
2) $CH_{3}-CH\left(C_{2}H_{5}\right)-CH=CH-CH_{2}-CH_{3}$ : $2-$éthylhex$-3-$ène
 
 
 
5) $CH_{3}-C\equiv C-CH\left(C_{2}H_{5}\right)-CH_{2}-CH_{2}-CH_{3}$ : $4-$éthylhépt$-2-$yne
 
6) $CH_{3}-CH_{2}-CH_{2}-CH\left(C_{2}H_{5}\right)-CH_{2}-C\equiv CH$ : $4-$éthylhépt$-1-$yne
 
7) $CH\equiv C-C\left(CH_{3}\right)_{2}-CH\left(C_{2}H_{5}\right)-CH_{3}$ : $4-$éthyl$-3.3-$diméthylpent$-1-$yne
 
B. Les formules des divers corps et leur nom dans les réactions suivantes :
 
$C_{2}H_{5}OH\ \rightarrow\ W+H_{2}O\Rightarrow C_{2}H_{5}OH\ \rightarrow\ CH_{2}=CH_{2}(\text{Ethène})+H_{2}O(\text{eau})$
 
$W+Cl_{2}\ \rightarrow\ X\Rightarrow CH_{2}=CH_{2}+Cl_{2}\ \rightarrow\ ClCH_{2}-CH_{2}Cl\ (1.2-\text{dichloroéthane})$
 
$X\ \rightarrow\ Y+HCl\Rightarrow ClCH_{2}-CH_{2}Cl\ \rightarrow\ CH_{2}=CHCl\ (\text{Chloroéthène ou chlorure de vinyl})+HCl$
 
$Y\ \rightarrow\ Z\text{ par polymérisation }nCH_{2}=CHCl\ \rightarrow\ \left(CH_{2}-CHCl\right)_{n}\ (\text{polychlorure de vinyle})$
 
Précisons l'intérêt du polymère obtenu
 
Ce polymère sert à la fabrication d'objets plastiques assez rigides, peu élastiques : tuyaux de canalisation, bouteilles d'eau et de lait, chaussures etc... 
 
Ils offrent une bonne résistance aux produits chimiques

Exercice 2

Écriture de la formule semi-développée des hydrocarbures suivants :
 
a) $3-$éthyl, $2-$méthylpent$-2-$ène : $CH_{3}-CH_{2}-CH\left(C_{2}H_{5}\right)= C\left(CH_{3}\right)-CH_{3}$ 
 
b) $3.6-$diéthyloct$-4-$yne : $CH_{3}-CH_{2}-CH\left(C_{2}H_{5}\right)-CH_{2}-C\equiv C\left(C_{2}H_{5}\right)-CH_{2}-CH_{3}$ 
 
c) $2.4-$diméthylpent$-2-$ène : $CH_{3}-CH=C\left(CH_{3}\right)-CH\left(CH_{3}\right)-CH_{3}$
 
d) hex$-2-$yne : hex$-2-$yne : $CH_{3}-C\equiv C-CH_{2}-CH_{2}-CH_{3}$
 
e) $1.2-$dibromocyclobutène :
 
f) $2-$chlorobuta$-1.3-$diène : $CH_{2}=CCl-CH=CH_{2}$
 
g) $4.6-$dipropylnon$-4-$ène : $CH_{3}-CH_{2}-CH_{2}-C\left(C_{3}H_{7}\right)=CH_{2}-CH\left(C_{3}H_{7}\right)-CH_{2}-CH_{2}-CH_{3}$
 
h) $6-$méthylhept$-2.4-$diyne : $CH_{3}-CH\left(CH_{3}\right)-C\equiv C-C-CH_{3}$
 
i) $3-$éthyl$-1.4-$diméthyl$-5-$tert$-$butyl$-2-$vinylcyclohexène : 
 
j) But$-3-$ène : $CH_{3}-CH_{2}-CH=CH_{2}$
 
k) $2-$éthylprop$-1-$ène : $CH_{3}-C\left(C_{2}H_{5}\right)=CH_{2}$
 
m) $2-$méthylcyclopentène :
 
n) Pent$-3-$yne : $CH_{3}-CH_{2}-C\equiv C-CH_{3}$
 
o) $Z–3.4–$diméthylpent$-2-$ène :
 
p) $E–3.4–$diméthylpent$-2-$ène :

Exercice 6

1. a) Détermination de la formule brute générale de cet hydrocarbure.
 
La formule brute générale de cet hydrocarbure est $C_{x}H_{y}$
 
\begin{eqnarray} \dfrac{m_{C}}{m_{H}} &=&\dfrac{12x}{y}\nonumber\\\\ &=&\dfrac{6m_{H}}{m_{H}}\nonumber\\\\\Rightarrow 6x &=& 12x\nonumber\\\\\Rightarrow y &=&2x\nonumber\\\\\Rightarrow C_{x}H_{2x} \end{eqnarray}
 
b) L'hydrocarbure appartient à la famille des cyclanes ou des alcènes.
 
c) Écriture des formules semi-développées possibles de $A$ sachant $A$ renferme $8$ atomes d'hydrogène.
 
$C_{x}H_{2x}$  pour  $2x=8\Rightarrow x=4\Rightarrow C_{4}H_{8}$
 
$\Rightarrow CH_{3}-CH_{2}-CH=CH_{2}$ ;
 
$CH_{3}-CH=CH-CH_{3}$ ;
 
$CH_{3}-C\left(CH_{3}\right)=CH_{2}$
 
 
2. La chaine carbonée de l'hydrocarbure $A$ est linéaire ; de plus $A$ possède des stéréo-isomères $Z/E.$
 
Représentation de ces stéréo-isomères.
 
 
3. a) Détermination de la composition centésimale molaire du mélange gazeux
 
\begin{eqnarray} \%C_{2}H_{4} &=&\dfrac{M_{C_{2}H_{4}}}{M_{\text{mélange}}}\times 100\nonumber\\\\ &=&\dfrac{28}{29\times 1.2068}\times 100\nonumber\\\\\Rightarrow \%C_{2}H_{8}\nonumber\\\\ &=& 80 \end{eqnarray}
 
$\%C_{4}H_{8}=100-80\Rightarrow \%C_{4}H_{8}=20$
 
b) Écriture des formules semi-développées et les noms des produits $B$ et $C$ formés. 
 
$B$ étant le produit issu de l'action du dichlore sur $A.$
 
$CH_{3}-CHCl-CHCl-CH_{3}\ (B)\ $ : $2\;\ 3-$dichlorobutane
 
$CH_{2}Cl-CH_{2}Cl\ (C)\ $ : $1\;\ 2-$dichlorobutane
 
Le composé $C$ donne le composé $D$ et le chlorure d'hydrogène.
 
Équation bilan
 
$CH_{2}Cl-CH_{2}Cl\ \rightarrow\ CH_{2}=CH_{2}Cl\ (D)\ +\ HCl$
 
d) La réaction produite est une réaction de polymérisation
 
$\left(CH_{2}-CH_{2}Cl\right)_{n}\ (E)\ $ : Polychlorure de vinyle
 
Intérêt du Polychlorure de vinyle.
 
Le Polychlorure de vinyle sert à la fabrication d'objets plastiques assez rigides, peu élastiques : tuyaux de canalisation, bouteilles d'eau et de lait, chaussures etc. 
 
Ils offrent une bonne résistance aux produits chimiques.

Exercice 9

1) Formule semi-développée de l'acétylène.
 
$HC\equiv CH$
 
L'acétylène appartient à la famille des alcynes
 
L'acétylène est un hydrocarbure insaturé parce qu'il contient une liaison multiple
 
2). Équation-bilan de la réaction et nom du produit $B$ formé.
 
$HC\equiv CH+Cl_{2}\ \rightarrow\ HCCl=CHCl\quad 1.2-$dichloroéthène
 
3) a) Équation de la réaction et nom du composé $E.$
 
$nHCCl=CHCl\ \rightarrow\ \left(HCCl-CHCl\right)_{n}\quad \text{Poly}-1.2-\text{dichloroéthène}$
 
b) Calcul du degré de polymérisation du polymère et $FSD$ de son motif.
 
$n=\dfrac{M_{E}}{M_{C_{2}H_{2}Cl_{2}}}=\dfrac{=67.5\cdot 10^{3}}{97}$
 
$\Rightarrow\,n=67\ -HCCl-CHCl-$
 
4) L'hydrogénation de l'acétylène conduit à un composé insaturé $C.$
 
L'hydratation du composé $C$ donne un composé $F.$
 
a) Précisons le catalyseur utilisé pour chacune des réactions.
 
Pour l'hydrogénation de l'acétylène conduisant à un composé insaturé $C$, il faut le palladium désactivé comme catalyseur et l'acide sulfurique pour le composé $C$ en composé $F$
 
b) Équations-bilans des différentes réactions.
 
$HC\equiv CH+H_{2}\stackrel{Pd}{\longrightarrow}H_{2}C=CH_{2}$
 
$H_{2}C=CH_{2}+H_{2}O\stackrel{H_{2}SO_{4}}{\longrightarrow}H_{3}C-CH_{2}OH$
 
c) Les familles de composés auxquels appartiennent $C$ et $F.$
 
Le composé $C$ appartient à la famille des alcènes et $F$ à la famille des alcools
 
$H_{2}C=CH_{2}\quad(C)$ : Ethène ; 
 
$H_{3}C-CH_{2}OH\quad(F)$ : Ethanol

 

Auteur: 
Sidy Mouhamed Ndiaye

Pages