Physique

Série d'exercices : Oscillations mécaniques libres - Ts

Classe: 
Terminale
 

Exercice 1 

Pendule élastique horizontal
 
On considère un ressort dont une extrémité est fixe et dont l'autre est reliée à un corps $M$ qui peut glisser sans frottement sur un plan horizontal (figure 1). 
 
 
Le corps $M$ est assimilé à une masse ponctuelle $m.$ 
 
Le ressort, de raideur $k$ et de masse négligeable, a une longueur au repos $\ell_{0}.$
 
1) Établir l'équation différentielle du mouvement du corps $M.$ 
 
On utilisera un axe $Ox$ dont l'origine $O$ correspond à la position de $M$ lorsque le ressort est au repos.
 
2) On considère les conditions initiales de mouvement suivantes :
 
a) $t=0$ le corps $M$ est en $x=x_{0}>0$ et la vitesse initiale de $M$ est nulle.
 
b) $t=0$ le corps $M$ est en $x=x_{0}$ et la vitesse de $M$ est $\overrightarrow{v_{0}}=v_{0}\overrightarrow{\mathrm{e_{x}}}$ avec $v_{0}>0.$
 
Déterminer l'équation horaire du mouvement du corps $M$ dans les cas a) et b).
 
Pendule élastique vertical
 
Un ressort identique à celui du 1) est lié à un corps $M$, supposé ponctuel et de masse $m$, qui peut se déplacer verticalement dans le champ de pesanteur terrestre.
 
 
1) Déterminer la position d'équilibre du corps $M.$
 
2) Établir l'équation différentielle du mouvement de $M.$

Exercice 2 

Oscillations d'un pendule simple
 
Un pendule simple est constitué d'une masse $m$ suspendue à un fil non élastique, de masse négligeable, de longueur $\ell.$ 
 
Il est écarté de sa position d'équilibre d'un angle $\theta_{0}$ et lâché sans vitesse initiale. 
 
On note $\theta$ l'angle que fait à l'instant $t$ la direction du pendule $OM$ avec l'axe $Ox$ (voir schéma).
 
 

1) Conservation de l'énergie

a) Donner l'expression de l'énergie cinétique $E_{c}(\dot{\theta})$, de l'énergie potentielle de pesanteur $E_{p}(\theta)$ et celle de l'énergie totale $E$ en tenant compte des conditions initiales. 
 
On prendra la référence de l'énergie potentielle à la position d'équilibre.
 
b) Établir l'équation différentielle du mouvement.

2) Petites oscillations

Dans tout ce qui suit, on se place dans le cas de petites oscillations : $\theta_{0}$ est suffisamment petit pour que l'on puisse poser $\sin\theta\approx\theta$ et $\cos\theta\approx 1-\dfrac{\theta^{2}}{2}.$
 
a) Résoudre l'équation différentielle vérifiée par $\theta(t)$ en tenant compte des conditions initiales. 
 
Quelle est la période des oscillations du pendule ?
 
b) Donner l'expression de l'énergie cinétique $E_{c}(t)$ et de l'énergie potentielle $E_{p}(t)$ en fonction du temps et vérifier la conservation de l'énergie. 
 
Montrer qu'en valeur moyenne dans le temps on a équipartition de l'énergie : $(E_{c})=(E_{p}).$
 
3) Amortissement du pendule
 
On tient compte maintenant de la viscosité de l'air qui est responsable d'une force de frottement de sens opposé à la vitesse : $\overrightarrow{F}=f\overrightarrow{v}$ où le nombre positif $f$ est le coefficient de frottement visqueux.
 
a) Donner la projection de l'équation fondamentale de la dynamique sur la base orthonormale $\overrightarrow{e_{r}}$ et $\overrightarrow{e_{\theta}}$ des coordonnées polaires du point $M$ (voir schéma) et en déduire l'équation différentielle du mouvement. 
 
Montrer que l'équation vérifiée par $\theta$ pour des mouvements de faible amplitude est de la forme :
$$\ddot{\theta}+\dfrac{\omega_{0}}{Q}\dot{\theta}+\omega_{0}^{2}\theta=0$$
 
où $Q$ est un nombre sans dimension appelé facteur de qualité de l'oscillateur et $\omega_{0}$ est la pulsation des oscillations non amorties.
 
b) Montrer que la solution de cette équation différentielle, avec les mêmes conditions initiales peut traduire différents comportements du pendule suivant la valeur du coefficient de frottement $f$ ; on examinera les cas suivants et on tracera le graphe de $\theta(t)$ :

$(i)\qquad\qquad Q>\dfrac{1}{2}\qquad (amortissement\ faible\ : \ régime\ oscillatoire)$

$(ii)\qquad\qquad Q<\dfrac{1}{2}\qquad (amortissement\ fort\ :\ régime\ hypercritique)$

$(iii)\qquad\qquad Q=\dfrac{1}{2}\qquad (régime\ critique)$
 
c) Bilan énergétique
 
Utiliser le théorème de l'énergie cinétique entre deux instants voisins $t$ et $t+\mathrm{d}t$ pour montrer que l'énergie du système $E=E_{c}+E_{p}$ diminue au cours du temps et interpréter ce résultat.

Exercice 3

 
Un solide, de masse $m=400g$, glisse sans frottements sur une table à coussin d'air horizontale.
 
Il est relié d'un côté à un ressort $R_{1}$ dont l'extrémité $A_{1}$ est fixe et de l'autre côté à $R_{2}$ dont l'extrémité $A_{2}$ est fixe.
 
Le ressort $R_{1}$, à l'équilibre, est allongé de $10\,cm$, $R_{2}$ est allongé de $8\,cm.$
 
1) Quelle est la constante de raideur $k_{2}$ de $R_{2}$, sachant que celle de $R_{1}$, $k_{1}$, est $40\,N\cdot m^{-1}.$
 
Le solide accomplit des oscillations de translation, parallèlement à $A_{1}A_{2}.$
 
2) a) Montrer que l'oscillateur est harmonique.
 
b) Calculer sa pulsation propre.
 
Le solide est écarté de $2\,cm$ de sa position d'équilibre, vers $A_{2}.$
 
De là, à $t=0$, on le lance vers $A_{1}$ à la vitesse de $0.1\,m\cdot s^{-1}.$
 
3) Quelle est la loi horaire du mouvement ?
 
L'état de référence pour l'énergie potentielle des deux ressorts est la position d'équilibre.
 
L'oscillateur est excité.
 
4) Calculer son énergie mécanique.

Exercice 4

Une tige homogène $OA$ de longueur $\ell=1m$, de masse $m=100\,g$ et de moment d'inertie par rapport à $\Delta$ $J=\dfrac{1}{3}m\cdot\ell^{2}$ peut osciller autour d'un axe horizontal $\Delta$, passant par son extrémité supérieure $O.$
 
 
1) Montrer que, si les l'amplitude des oscillations est suffisamment faible, ces dernières sont forcément harmoniques.
 
2) Déterminer la pulsation propre de cet oscillateur.
 
A l'extrémité de la tige, en $A$, on fixe une masse pratiquement ponctuelle, $m'.$
 
La période des oscillations de faible amplitude est $T'=1.83s.$
 
3) Déterminer $m'.$
 
On retire la masse $m'.$
 
La tige est soudée en $O$ à un fil de torsion $OO'$, colinéaire à $\Delta$, l'axe de rotation horizontal de la barre.
 
Le fil $OO'$ a pour constante de torsion $C=0.2\,N\cdot m\cdot rad^{-1}$, il n'est pas tordu lorsque $OA$ est verticale.
 
4) a) Montrer que cet oscillateur n'est pas harmonique, mais qu'il peut être linéarisé.
 
b) Calculer dans ce cas sa pulsation propre.

Exercice 5 : Pendule et ressort

On considère une masse ponctuelle accrochée à l'extrémité d'un ressort de longueur $l$ dont le point de suspension est fixé en $O$, Cette masse $m$ est de plus accrochée à l'extrémité d'un ressort de raideur $k$ dont l'autre extrémité au point $A.$
 
A l'équilibre le ressort est horizontal et la masse est située en $O$ à la verticale du point de suspension du pendule (voir figure)
 
On supposera que le mouvement du pendule a lieu dans un plan (SCHEMA)
 
1 a) Établir l'équation différentielle qui régit le mouvement de la masse ponctuelle dans l'approximation des petits angles
 
b) En déduire les expressions de la période de la période et de la pulsation propre
 
2 a) Exprimer l'énergie potentielle du pendule supposé seul en fonction de l'angle $\theta$
 
On prendra l'origine de l'énergie potentielle à l'équilibre
 
b) Exprimer l'énergie potentielle du ressort supposé seul lorsqu'on écarte de l'angle $\theta$
 
c) Sachant que l'énergie potentielle totale est la somme de deux termes calculés précédemment ; déduire son expression dans l'approximation des petits angles $(\cos\theta\approx 1-\theta^{2}/2\;,\ \sin\theta\approx\theta)$ 
 
d) Exprimer l'énergie cinétique du pendule en fonction de l'angle $\theta.$
 
En déduire une expression de l'énergie totale du système dans l'approximation des petits angles
 
e) En déduire l'équation différentielle du mouvement. 
 
Déterminer la pulsation du mouvement de la masse $m$ dans l'approximation des petits angles.

Exercice 6

Un solide $(S)$ de masse $m$ est attaché à l'une des extrémités d'un ressort horizontal parfaitement élastique, de constante de raideur $k$ et de masse négligeable devant celle du solide $(S).$ 
 
L'autre extrémité du ressort est fixe.
 
On écarte le solide $(S)$ de sa position d'équilibre de $x_{0}$ à un instant qu'on prend comme origine des dates, puis on l'abandonne sans vitesse. 
 
On néglige les frottements et on étudie le mouvement du solide $(S)$ relativement à un repère galiléen $(O\;,\ \vec{i})$ d'origine $O$, la position du centre d'inertie de $(S)$ à l'équilibre et d'axe $ox$ horizontal (figure 1).
 
 
1) a) A une date $t$ quelconque, le centre d'inertie $G$ de $(S)$ a une élongation $x$ et sa vitesse instantanée est $v.$ 
 
Établir l'expression de l'énergie mécanique $E$ du système $\{$solide $(S)$, ressort$\}$ en fonction de $x$, $v$, $k$ et $m.$
 
b) Montrer que cette énergie mécanique $E$ est constante. 
 
Exprimer sa valeur en fonction de $k$ et $x_{0}.$
 
c) En déduire que le mouvement de $(S)$ est rectiligne sinusoïdal
 
2) A l'aide d'un dispositif approprié, on mesure la vitesse instantanée $v$ du solide $(S)$ pour différentes élongations $x$ du centre d'inertie $G$ de $(S).$ 
 
Les résultats des mesures ont permis de tracer la courbe $v^{2}=f(x^{2})$ (figure 2)
 
 
a) Justifier théoriquement l'allure de la courbe en établissant l'expression de $v^{2}.$
 
b) En déduire les valeurs de :
 
$-\ $ la pulsation $\omega_{0}$ et l'amplitude $x_{0}$ du mouvement de $(S)$,
 
c) Établir l'équation horaire du mouvement.
 
d) Sachant que l'énergie mécanique $E$ du système est égale à $0.0625\,J$, calculer les valeurs de la constante de raideur $k$ du ressort et la masse $m$ du solide

Exercice 7

Partie A : 
 
Un pendule élastique horizontal est constitué par un solide $(S)$ de masse $m=500\,g$, attaché à l'une des extrémités d'un ressort horizontal, parfaitement élastique, de raideur $K$ et de masse négligeable par rapport à celle du solide, l'autre extrémité du ressort étant fixe (figure 1). 
 
On néglige tout type de frottement et on étudie le mouvement du solide $(S)$ relativement à un repère galiléen $(O\;,\ \vec{i})$ horizontal, d'origine $O$ coïncidant avec la position d'équilibre du centre d'inertie du solide.
 
On écarte le solide $(S)$ de sa position d'équilibre d'une distance $X_{m}$ puis on le lâche sans vitesse. 
 
Lorsque le solide passe par sa position d'abscisse $x_{0}$ $(x_{0}\neq 0)$ avec une vitesse initiale $v_{0}$ $(v_{0}\neq 0)$ en se dirigeant dans le sens positif, on déclenche le chronomètre $($c'est l'instant $t=0s)$ pour commencer l'étude du mouvement.
 
1) a) En appliquant la relation fondamentale de la dynamique au solide $(S)$, établir l'équation différentielle de son mouvement. 
 
Quelle est la nature de ce mouvement ?
 
b) Montrer que $x(t)=X_{m}\sin(\omega_{0}t+\varphi_{x})$ est une solution de l'équation différentielle précédente à condition que la pulsation $\omega_{0}$ vérifie une expression qu'on donnera en fonction de $K$ et $m.$
 
Donner l'expression de la période propre $T_{0}$ des oscillations du solide $(S).$
 
c) Déduire l'expression de la vitesse du solide en fonction de $X_{m}$, $\omega_{0}$, $t$ et $\varphi_{x}.$
 
2) Montrer que $x_{0}$ et $v_{0}$ vérifient la relation $x_{02}+\dfrac{v_{0}^{2}}{\omega_{0}^{2}}=X_{m}^{2}$
 
3) Un ordinateur muni d'une interface et d'un capteur a enregistré les variations de l'énergie cinétique du solide $(S)$ au cours du temps $t$, le graphe obtenu sur l'écran de l'ordinateur est donné par la figure 2.
 
 
a) Donner l'expression de l'énergie mécanique $E$ du système $S_{0}=\{(S)+\text{ressort}\}$ en fonction de $x$, $v$, $K$ et $m$ avec $x$ élongation du solide $(S)$ et $v$ sa vitesse à un instant $t$ quelconque.
 
Montrer que l'énergie $E$ est constante puis donner son expression en fonction de $m$ et $V_{m}$ ; $V_{m}$ amplitude de la vitesse $v$ du solide.
 
Établir l'expression de l'énergie cinétique du solide $(S)$ en fonction $m$, $V_{m}$, $\omega_{0}$, $t$ et $\varphi.$
 
Montrer qu'on peut l'écrire sous la forme : $$E_{c}=\dfrac{E_{c\,max}}{2}(1+\cos(2\omega_{0}t+2\varphi_{x}))$$
 
b) En utilisant le graphe, trouver :
 
$-\ $ L'amplitude de la vitesse $V_{m}.$
 
$-\ $ La période propre $T_{0}.$
 
En déduire $X_{m}.$
 
$-\ $ La phase initiale $\varphi_{x}$ de l'élongation $x(t).$
 
c) Écrire la loi horaire du mouvement.
 
d) Calculer l'abscisse initiale $x_{0}(x(t=0))$ du solide $(S)$ dans le repère $(O\;,\ \vec{i})$, déduire sa vitesse initiale $v_{0}.$ 
 
Dans quel sens débute le mouvement du solide $(S)$ ?
 
e) Calculer la raideur $K$ du ressort.

Partie B :

Dans cette partie, le solide $(S)$ est soumis à une force de frottement visqueux $f=-h\overrightarrow{v}$ ou $h$ est une constante positive $h$ $(h=0.2$ u.s.i$).$
 
1) Donner le nom et l'unité de $h.$
 
2) Établir l'équation différentielle du mouvement du solide $(S)$ régissant les variations de son élongation $x(t).$
 
3) Montrer que l'énergie totale du système $S_{0}=\{(S)+\text{ressort}\}$ diminue au cours du temps.
 
4) À l'aide d'un dispositif approprié, on a enregistré les variations de la vitesse du solide en fonction du temps ; on a trouvé le graphe de la figure 3 :
 
Calculer l'énergie dissipée par la force de frottement entre les instants $t_{1}$ et $t_{2}.$

Exercice 8

Un pendule élastique est constitué d'un ressort à spires non jointives, de masse négligeable et de constante de raideur $K$, et d'un solide $(S)$ supposé ponctuel de masse $m.$ 
 
Le solide $(S)$ peut se déplacer sans frottement sur un plan horizontal. 
 
Sa position est repérée par son abscisse $x$ dans le repère $(O\;,\ \vec{i})$ avec $O$ la position d'équilibre de $(S)$ (figure 1).
 
 
On soumet $(S)$ à une force excitatrice $\overrightarrow{F}=\overrightarrow{F}\cdot\vec{i}=F_{m}\sin(\omega\,t+\varphi_{F})\vec{i}$ et à une force de frottement $\overrightarrow{f}=-h\overrightarrow{v}$ avec $\overrightarrow{v}$ la vitesse de $(S)$ et $h$ une constante positive.
 
1) Établir l'équation différentielle régissant les variations de l'élongation $x.$
 
Pour une certaine valeur $h_{1}$ de $h$ et une valeur $\omega_{1}$ de $\omega$, on obtient les courbes de variations de $F$ et de $x$ en fonction de temps (figure 2).
 
 
a) Montrer que la courbe $\mathcal{C_{1}}$ correspond à $F(t).$
 
b) Déterminer la valeur de $\omega_{1}$, $F_{m}$, $X_{m}$, et $\varphi_{F}-\varphi_{x}.$
 
c) Quelle est la valeur de $\varphi_{F}$ ? 
 
Déduire celle de $\varphi_{x}.$
 
d) Faire la construction de Fresnel correspondante. 
 
Déduire les expressions de $X_{m}$ et de $\sin(\varphi_{F}-\varphi_{x}).$
 
Calculer $h_{1}.$
 
Pour une certaine valeur $\omega_{r}$ de $\omega$, on constate que $X_{m}$ prend sa valeur la plus élevée.
 
a) Dans quel état se trouve l'oscillateur ?
 
b) On donne la courbe de variation de $\omega_{r}^{2}$ en fonction de $h^{2}$ (figure 3) ainsi que l'expression de $\omega_{r}=\sqrt{-\dfrac{h^{2}}{2m^{2}}+\dfrac{K}{m}}.$
 
 
Déterminer $K$ et $m.$
 
2) En précisant l'analogie utilisée donner :
 
a) Le schéma du montage du circuit électrique analogue à l'oscillateur mécanique précédent.
 
b) L'expression de la charge maximale $Q_{m}$ du condensateur.
 
c) L'expression de la pulsation $\omega_{r}$ correspondant à la valeur la plus élevée de $Q_{m}.$

Exercice 9

Un solide $(C)$ supposé ponctuel de masse $m$ est accroché libre d'un ressort de masse négligeable et de constante de raideur $K$
 
On écarte verticalement $(C)$ d'une distance $a$ par rapport à sa position d'équilibre et on l'abandonne à lui-même sans vitesse à l'instant $t=0s$
 
La position de $(C)$ est repérée par rapport à sa position d'équilibre ; à l'instant $t$ par l'abscisse $x$ (figure 1)
 
1) Montrer que l'énergie potentielle du système $S$ $(C$, Terre ; ressort$)$ à l'instant sous la forme $E_{p}=\dfrac{1}{2}\left(x^{2}+\Delta\,l_{0}^{2}\right)$ avec $\Delta\,l_{0}$ étant l'allongement du ressort à l'équilibre
 
2) On donne la représentation graphique $E_{p}=f(x^{2})$ ( figure 2)
 
a) Déterminer graphiquement $a$, $k$, $\Delta\,l_{0}$
 
b) En déduire $m$
 
3) a) Montrer que le système est conservatif.
 
b) Exprimer l'énergie mécanique du système $(S)$ en fonction de ; $a$ et $k.$
 
c) En déduire l'énergie cinétique de $(S)$ à l'instant $t$ en fonction $k$, $a$ et $x.$

Exercice 10

Une masse $m$ est susceptible de se déplacer sans frottements sur un axe horizontal. 
 
Elle est soumise à l'action de $2$ ressorts de même longueur à vide $l_{0}=20cm$ et de constantes de raideur différentes $k_{1}$ et $k_{2}.$
 
On donne : 
 
$m=4kg$ ; $k_{1}=100N\cdot m^{-1}$ ; $k_{2}=300N\cdot m{-1}$ et $d=60cm.$
 
 
1. Déterminer les longueurs $l_{1}$ et $l_{2}$ des $2$ ressorts à l'équilibre.
 
2. On écarte la masse $m$ d'une distance $x$ à partir de sa position d'équilibre.
 
Déterminer l'équation différentielle du mouvement en prenant la position d'équilibre comme origine des abscisses.
 
2.1 Calculer la période et la fréquence des oscillations.
 
2.2 Donner l'expression de l'énergie mécanique de la masse.
 
On prendra la position d'équilibre comme état de référence pour l'énergie potentielle de pesanteur et la position du ressort à vide pour l'énergie potentielle élastique
 
2.3 Retrouver l'équation différentielle en utilisant la conservation de l'énergie mécanique
 
3. Les ressorts sont tendus le long d'un plan incliné de $\alpha=30^{\circ}$ avec l'horizontale
 
Mêmes questions.

Exercice 11

Un solide $(S)$ de masse $m$ est attaché à l'une des extrémités d'un ressort horizontal parfaitement élastique, de constante de raideur $k$ et de masse négligeable devant celle du solide $(S).$ 
 
L'autre extrémité du ressort est fixe. 
 
On écarte le solide $(S)$ de sa position d'équilibre de $x_{0}$ à un instant qu'on prend comme origine des dates, puis on l'abandonne sans vitesse.  
 
On néglige les frottements et on étudie le mouvement du solide $(S)$  relativement à un repère galiléen $(O\;,\ \vec{i})$ d'origine $O$, la position du centre d'inertie de $(S)$ à l'équilibre et d'axe $ox$ horizontal (fig. 1).
 
 
1) a) A une date $t$ quelconque, le centre d'inertie $G$ de $(S)$ a une  élongation $x$ et sa vitesse instantanée est $v.$ 
 
Établir l'expression de l'énergie mécanique $E$ du système $\{\text{solide (S), ressort}\}$ en fonction de $x$, $v$, $k$ et $m.$
 
b) Montrer que cette énergie mécanique $E$ est constante.  
 
Exprimer sa valeur en fonction de $k$ et $x_{0}.$
 
c) En déduire que le mouvement de $(S)$ est rectiligne sinusoïdal.
 
2) A l'aide d'un dispositif approprié, on mesure la vitesse instantanée $v$ du  solide $(S)$ pour différentes élongations $x$ du centre d'inertie $G$ de $(S).$
 
Les résultats des mesures ont permis de tracer la courbe $v^{2}=f(x^{2})$  (fig. 2).
 
 
a) Justifier théoriquement l'allure de la courbe en établissant l'expression de$v^{2}.$
 
b) En déduire les valeurs de la pulsation $\omega_{0}$ et l'amplitude $x_{0}$  du  mouvement de $(S)$
  
c) Établir l'équation horaire du mouvement.
 
d) Sachant que l'énergie mécanique $E$ du système est égale à $0.0625J$, calculer les valeurs de la constante de raideur $k$ du ressort et la masse $m$ du solide

Exercice 12

Le pendule élastique horizontal de la figure 1 est constitué par un solide $(S)$ de masse $m=0.2Kg$ soudé à l'une des extrémités d'un ressort $(R)$ à spires non jointives de masse négligeable et de constante de raideur $K$, l'autre extrémité est attaché à un support fixe. 
 
A l'équilibre, le centre d'inertie $(G)$ du solide $(S)$ coïncide avec l'origine $O$ d'un repère espace horizontal $(O\;,\ \vec{i}).$
 
 

Partie A

A partir du point $O$, on écarte le solide $(S)$ vers un point $A$ d'abscisse $x_{A}$ et à la date $t=0s$, on l'abandonne à lui-même sans vitesse initiale. 
 
Au cours de son mouvement, le solide $(S)$ se déplace sans frottement et son centre d'inertie $(G)$ est repéré par l'élongation $OG=x(t).$ 
 
Un système d'acquisition de données, enregistre les variations de l'élongation $x$ au cours du temps (Voir figure 2).
 
 
1) En utilisant le graphe 
    
a) Préciser la nature de mouvement de $(S).$
 
b) Déterminer l'abscisse initiale $x_{A}$ du solide $(S)$ et la constante de raideur $K$ du ressort.
 
c) Dans quel sens, débute le mouvement du solide $(S).$
 
2) Écrire la loi horaire $x=f(t)$ de mouvement du solide. 
 
Déduire l'équation différentielle du mouvement.
 
3) L'énergie cinétique du solide $E_{c}=\dfrac{mv^{2}}{2}$ varie au cours du temps selon une fonction sinusoïdale de période $T$
 
a) Établir l'expression de $E_{C}$ en fonction du temps.
 
b) Donner la valeur de $T.$
 
4) L'énergie mécanique du système $=\{\text{solide + ressort}\}$ est $E=E_{c}+E_{p}$ avec $E_{p}=\dfrac{Kx^{2}}{2}.$
 
a) Montrer que cette énergie est constante.
 
b) Comment apparaît cette énergie aux instants $t_{1}=0s$, $t_{2}=\dfrac{\pi}{16}s\ $ et $\ t_{3}=\dfrac{\pi}{8}s.$

Partie B

L'oscillateur est maintenant soumis à des forces de frottements visqueux équivalents à une force unique $\overrightarrow{f}=-h\overrightarrow{V}.$
 
Avec $h$ est une constante positive.
 
1) Établir l'équation différentielle vérifiée par l'élongation $x$ de $(G).$
 
2) Montrer que l'énergie totale du système $=\{\text{solide + ressort}\}$ diminue au cours du temps.
 
3) A l'aide d'un dispositif approprié, on a enregistré le diagramme d'espace de mouvement du solide, le résultat est donné par le graphe de la figure 3.
 
 
a) Quel est le nom du régime d'oscillations ?
 
b) Sachant que la variation de l'énergie totale du système $\{\text{solide + ressort}\}$ est égal au travail de la force de frottement. 
 
Calculer ce travail entre les instants $t_{1}=0s$ et $t_{2}=\dfrac{7\pi}{8}$

Exercice 13

Un ressort à spire non jointives, de constante de raideur $K$, de masse négligeable, est posé sur un plan horizontal. 
 
L'une des extrémités du ressort est fixe, l'autre est attachée à un solide $(S)$ de masse $m.$ 
 
Au cours de son mouvement, le solide $(S)$ est  soumis à une force de frottement de la forme $\overrightarrow{f}=-h\overrightarrow{v}=(h$ : est une constante positive de valeur  $h=0.1$  U.S.I$)$
 
 
1) L'abscisse $x$ du solide $(S)$ dans le repère $(O\;,\ \vec{i})$ vérifie l'équation différentielle $$0.5\cdot \dfrac{d^{2}x}{\mathrm{d}t^{2}}+0.05\cdot\dfrac{\mathrm{d}x}{\mathrm{d}t}+5\cdot x=0$$
 
a) Que représente $h$ ?  
 
Préciser son unité dans le système international.
 
b) Déterminer la masse $m$ du solide $(S)$ et la raideur $K$ du ressort.
 
2) On écarte le solide $(S)$ de sa position d'équilibre vers une position d'abscisse $x_{0}$ puis on le lâche sans vitesse initiale à l'origine des dates.  
 
L'abscisse $x$ varie selon la courbe de la figure 1.
 
a) Déterminer graphiquement la pseudo période $T$ des oscillations et l'abscisse initiale $x_{0}$ du solide.
 
b) Établir l'expression de l'énergie mécanique du système $S_{0}\ :\ \{\text{Solide, ressort}\}$, le plan horizontal passant par le centre d'inertie $G$ du solide est pris comme plan de référence de l'énergie potentielle de pesanteur.
 
c) Montrer que la variation de l'énergie mécanique du système $S_{0}$ est égale au travail de $\overrightarrow{f}$
  
d) Calculer ce travail entre la date initiale $(t=0)$ et la date où le solide a effectué deux oscillations et demie.
 
3) Sur la figure 1) b) on a représenté les graphes des énergies en fonction du temps, identifier les courbes représentées et compléter la courbe qui manque.
 
4) On a répété l'expérience précédente pour $3$ valeurs différentes de $h$ tel que : $h_{1}=15$ ; $h_{2}=2$ et $h_{3}=5$ et on a représenté sur la figure 2 dans un ordre quelconque  et à la même  échelle, les variations de $X(t).$
 
a) Attribuer à chaque courbe la valeur de $h_{i}$ correspondante ?
 
b) Donner le nom de chaque régime observé.
 
 

Exercice 14

L'extrémité d'un ressort $(R)$, est liée à un solide ponctuel de masse $m$, l'autre extrémité étant fixe. 
 
Ce solide peut glisser sans frottement sur un plan horizontal. 
 
Le ressort est à spires non jointives, de masse négligeable et de constante de raideur $k.$
 
On écarte le solide de sa position d'équilibre dans le sens  positif d'une distance de $4\,cm$ puis on le lâche sans vitesse initiale. 
 
La position d'équilibre est choisie comme origine du repère $(O\;,\ \vec{i}).$
 
 
1) a) Exprimer l'énergie mécanique à un instant $t$ quelconque du système $S$ : {Solide, ressort}.
 
b) Montrer que le mouvement solide est rectiligne sinusoïdal de pulsation $\omega_{0}.$
 
Donner l'expression de $\omega_{0}$
 
2) a) Déterminer l'expression de l'énergie cinétique $E_{C}$ du  solide en fonction du temps. 
 
Montrer que cette énergie est une fonction périodique.
 
b) Déterminer l'expression de l'énergie potentielle $E_{p}$ du système $S$ en fonction du temps.  
 
Montrer que cette énergie est une fonction périodique.
 
3) On donne la représentation graphique de l'énergie cinétique $E_{C}$ du solide en fonction du temps :
 
a) Déterminer la constante de raideur $k$ du ressort et la période $T_{0}$ de l'oscillateur.
 
b) Déterminer la masse $m$ du solide et l'équation horaire du mouvement du solide.
  
c) Représenter la courbe de l'énergie potentielle $E_{p}=f(t).$
 
Justifier le traçage de cette courbe.

Exercice 15

Un solide $(S)$ de masse $m$ est attaché à l'extrémité d'un ressort à spires non jointives de masse négligeable et de raideur $K=20N\cdot m^{-1}$, l'autre extrémité du ressort est attachée à un point fixe. 
 
Le système $S_{0}=\{(S)+\text{ressort}\}$ est placé sur un plan horizontal (figure 1). 
 
 
Au repos, le centre d'inertie $G$ du solide est au point $O$, origine d'un repère $(O\;,\ \vec{i})$ horizontal. 
 
A partir de $O$, on écarte le solide $(S)$ d'une distance $X_{m}$ dans le sens positif et on le lâche sans vitesse. 
 
1) a) Représenter les forces exercées sur le solide $(S)$ en mouvement à une date $t$ quelconque.
 
b. Établir l'équation différentielle du mouvement et déduire l'expression de la pulsation propre $\omega_{0}$ de l'oscillateur.
 
c) On donne le graphe représentant les variations de l'accélération du solide $(S)$ en fonction de l'élongation $x$ (figure 2).

 
Déterminer graphiquement $\omega_{0}.$ 
 
Montrer que la masse du solide est $m=200g.$
 
2) a) Au passage du solide $(S)$ par une position d'abscisse $x$ sa vitesse est $v$, donner l'expression de l'énergie mécanique totale $E$ du système $S_{0}$ en fonction de $m$, $v$, $K$ et $x.$
 
b) Montrer que l'énergie $E$ est constante puis l'exprimer en fonction de $K$ et $Xm.$
 
3) On donne le graphe qui représente les variations de l'énergie cinétique $E_{c}$ du solide en fonction du temps (figure 3). 
 
 
La loi horaire du mouvement est donnée par $x(t)=X_{m}\sin(\omega_{0}t+\varphi)$
 
a) Montrer que l'énergie cinétique $E_{c}$ s'écrit sous la forme $E_{c}=1/4KX^{2}m(1+\cos(2\omega_{0}t+2\varphi).$
 
b) A partir du graphe, déduire les valeurs de $X_{m}$ et $\varphi$ puis écrire, en fonction du temps, la loi horaire du mouvement

Exercice 16

Partie A 

Un solide $(S)$ de masse $m$ est attaché à l'une des extrémités d'un ressort horizontal, parfaitement élastique, de constante de raideur $K$ et de masse négligeable devant celle du solide, l'autre extrémité du ressort étant fixe (fig 1).
 
 
On étudie le mouvement du solide $(S)$ relativement à un repère galiléen $(o\;,\ \vec{i})$ horizontal, d'origine $O$ coïncidant avec la position d'équilibre du centre d'inertie du solide.
 
On écarte le solide $(S)$ de sa position d'équilibre dans le sens positif d'une distance $X_{m}=3\,cm$ puis on le lâche sans vitesse.
 
1) a) En appliquant la relation fondamentale de la dynamique au solide $(S)$, montrer que son mouvement est rectiligne sinusoïdal, de pulsation $\omega_{0}$ qu'on donnera son expression en fonction de $K$ et $m.$
 
b) A un instant $t$ quelconque, le centre d'inertie $G$ de $(S)$ a une élongation $x$ et sa vitesse instantané est $v.$
 
Établir l'expression de l'énergie mécanique $E$ du système $S_{0}=\{(S)+\text{ressort}\}$ en fonction $x$, $v$, $k$ et $m.$
 
c) Montrer que l'énergie $E$ est constante puis donner son expression en fonction de $k$ et $X_{m}.$
 
2) La solution de l'équation différentielle est $X(t)=X_{m}\sin(\omega_{0}t\varphi)$, déterminer l'expression de l'énergie potentielle $S_{0}$ en fonction de $K$, $X_{m}$, $\omega_{0}$, $t$ et $\varphi.$
 
Donner l'expression de sa période en fonction de $K$ et $m.$
 
3) On donne la représentation graphique de l'énergie potentielle $E_{p}$ (figure 2) en fonction du temps, déduire :
 
 
a) La constante de raideur $K$ du ressort et la période propre $T_{o}.$
 
Déduire la masse $m$ du solide.
 
b) la loi horaire de mouvement du solide $S$

Partie B

Dans cette partie, le solide $(S)$ est soumis à une force de frottement visqueux $\overrightarrow{f}=-h\overrightarrow{v}$ ou $h$ est une constante positive.
 
1) Établir l'équation différentielle de mouvement du solide $(S)$ régissant les variations de son élongation $X(t).$
 
2) Montrer que l'énergie totale du système $S_{0}=\{(S)+\text{ressort}\}$ n'est pas conservée.
 
3) A l'aide d'un dispositif approprié; on a enregistré les variation de l'élongation en fonction du temps ; on a trouvé le graphe de la figure 3 :
 
 
Calculer l'énergie dissipée par la force de frottement entre les instants $t_{1}$ et $t_{2}.$

Exercice 17

Un solide $(S)$ de masse $m$ est soudé à l'extrémité d'un ressort $(R)$ à spires non jointives de raideur $k.$ 
 
Le solide $(S)$ peut glisser sans frottement sur un plan horizontal.
 
Le centre d'inertie $G$ de $(S)$ est repéré sur un axe horizontal $X'OX$ dont $O$, l'origine, correspond à la position de repos de $(S).$
 
Le ressort est allongé à une abscisse $x_{0}$ et lâché à l'instant $t_{0}.$
 
Un dispositif permet d'enregistrer la variation de l'abscisse $X$ en fonction du temps donne la figure ci-dessous
 
 
1) Déterminer à partir du graphe la période $T_{0}$ et la pulsation $\omega_{0}$ du mouvement ?
 
2) a) Établir l'équation différentielle du mouvement du solide.
 
En déduire une relation entre $\omega_{0}$, $m$ et $k.$
 
b) Établir l'équation horaire du mouvement de $(S).$
 
3) Donner l'expression de l'énergie potentielle élastique du système $\{\text{solide (S), ressort (R)}\}$ en fonction de $t.$
 
Sachant que cette valeur à l'instant $t=0s$ est égale à $6.25\cdot 10^{-4}j$
 
a) Déterminer la valeur de $k.$
 
b) Quelle est la valeur de la masse $m$ ?
 
4) On se propose d'augmenter la période propre $T_{0}$ de l'oscillateur tout en conservant $k$ et $X_{m}$, pour cela on remplace la masse de solide $(S)$ par $M>m.$ 
 
On donne la courbe de l'énergie potentielle élastique du système ${\text{solide }(S)\;,\text{ ressort }(R)}$ en fonction de $t.$ 
 
 
a) Déterminer la nouvelle période propre du système oscillateur $T$
 
b) En déduire la masse $M$

Exercice 18

On considère l'oscillateur mécanique représenté sur la figure ci-dessous :
 
 
$(R)$ : ressort à spires non jointives, de masse négligeable et de raideur $K.$
 
$(C)$ : cylindre de masse $m$ pouvant glisser sans frottements sur une tige horizontale.
 
Écarté de sa position d'équilibre, puis libéré à lui-même, le solide se met à osciller.
 
A un instant de date $t$, le centre d'inertie du solide passe par la position d'abscisse $x$ relativement au repère $(O\;,\ \vec{i})$ avec la vitesse $v$
 
1) Établir l'équation différentielle vérifiée par la variable position $x(t)$
 
2) Vérifier que la solution de l'équation différentielle établie précédemment dans 1) est $x(t)=X_{m}\sin(\omega_{0}t+\varphi)$ ; en déduire l'expression de $\omega_{0}$
 
3) Un dispositif non représenté sur la figure a permis de tracer la courbe de la figure 2 donnant les variations de l'élongation $x$ en en fonction du temps.
 
 
a) En exploitant la courbe, établir l'équation horaire $x(t)$
 
b) Déduire l'expression $v(t)$ de la vitesse instantanée.
 
Représenter $v(t)$ sur la figure 2 à l'échelle $1$ div $\rightarrow\ 0.1m\cdot s^{-1}.$
 
c) Montrer qu'à chaque instant, $x$ et $v$ vérifie la relation :
 
$100x^{2}+v^{2}=0.16$ avec $x$ en $m$ et $v$ en $m\cdot s^{-1}.$
 
d) Déterminer la valeur de la vitesse du centre d'inertie du solide quand ce dernier passe par le point d'abscisse $x=2cm$ dans le sens négatif
 
e) On donne la masse $m$ du cylindre $(m=100g)$ ; déterminer la raideur $K$ du ressort
 
4) a) Exprimer l'énergie mécanique $E$ du système (solide, ressort) en fonction de $x$ et $v$ et des caractéristiques de l'oscillateur.
 
b) Montrer que $E$ est constant et calculer sa valeur observée.
 
c) Monter que l'énergie mécanique de l'oscillateur n'est plus constante. 
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Oscillations électriques libres et oscillations électriques forcées - Ts

Classe: 
Terminale
 

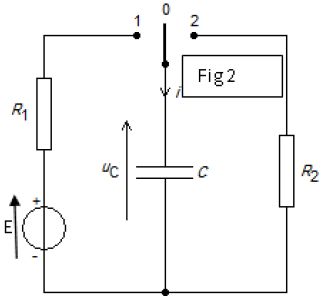
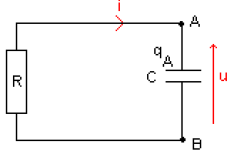
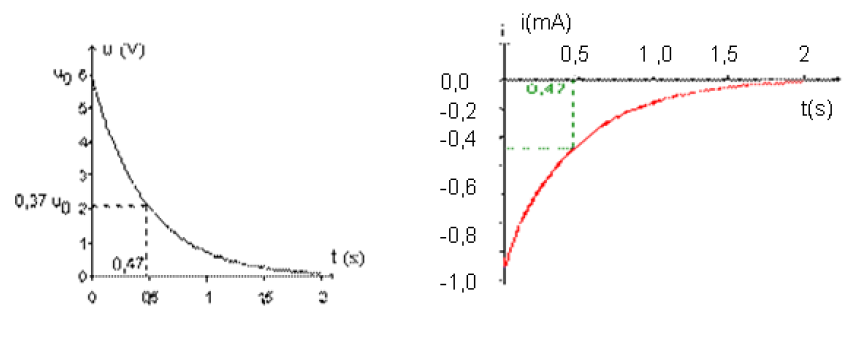
Exercice 1

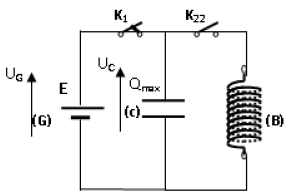
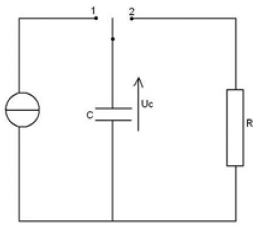
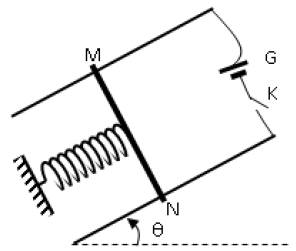
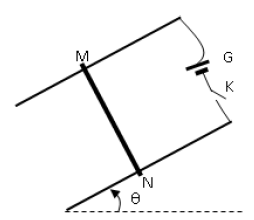
On considère le circuit électrique schématisé dans la figure ci-dessous,
 
 
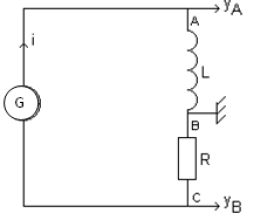
comportant : un générateur de tension continue $(G)$, de $f.é.m$ $U_{0}$ et de résistance interne négligeable ; un condensateur $(c)$ de capacité $C$ et d'armatures $A$ et $B$ ; une bobine $(B)$ d'inductance $L$ et de résistance négligeable ; deux interrupteurs $K_{1}$ et $K_{2}.$
 
1) $K_{2}$ étant ouvert, on ferme $K_{1}.$ 
 
Après une brève durée, le condensateur porte une charge maximale $Q_{0}$ et emmagasine une énergie électrostatique $E_{0}.$
 
a) Donner l'expression de $Q_{0}$ en fonction de $U_{0}$ et $C.$
 
b) Donner l'expression de $E_{0}$ en fonction de $Q_{0}$ et $C.$
 
2) Le condensateur étant chargé ; à $t=0$ on ouvre $K_{1}$ et on ferme $K_{2}.$ 
 
A $t$ quelconque, l'armature $A$ du condensateur porte une charge $q.$
 
a) Exprimer l'énergie électromagnétique $E$ en fonction de $L$, $C$, $q$ et $i.$
 
b) Montrer, sans faire aucun calcul que cette énergie se conserve et elle est égale à $\dfrac{Q_{0}^{2}}{2C}$
 
Déduire l'équation différentielle des oscillations électriques.
 
c) Déterminer l'expression de la période propre $T_{0}$ en fonction de $L$ et $C.$
 
d) Donner l'expression de la charge $q$ en fonction du temps.
 
3) Montrer que l'expression de cette énergie $E_{L}$ en fonction du temps s'écrit :
$$E_{L}=\dfrac{E_{0}}{2}\left[1+\cos\left(\dfrac{4\pi}{T_{0}}t+\pi\right)\right]$$
 
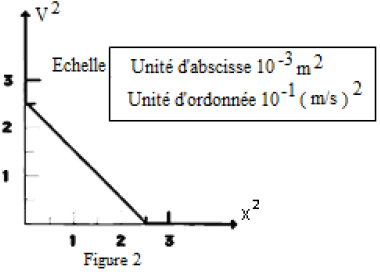
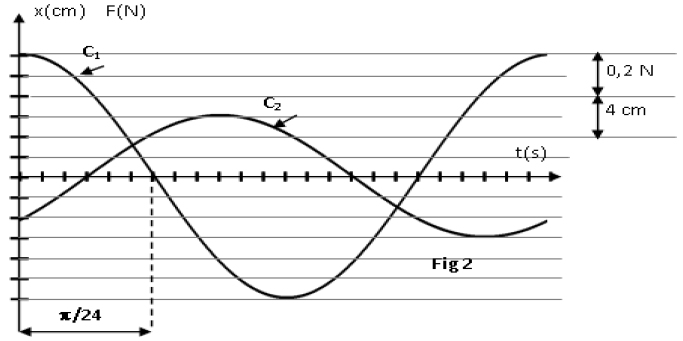
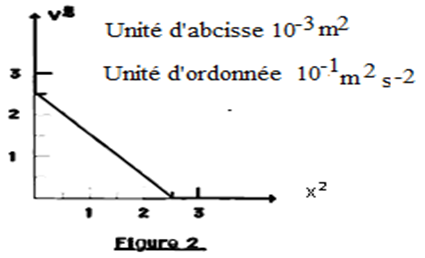
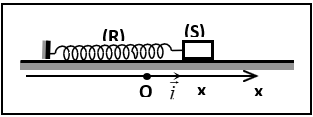
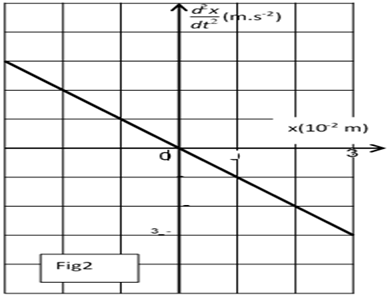
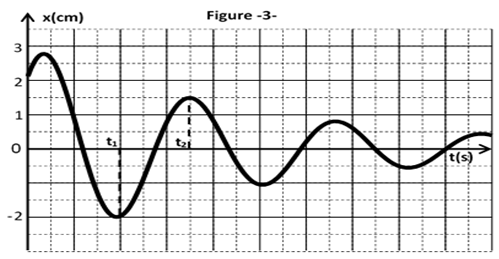
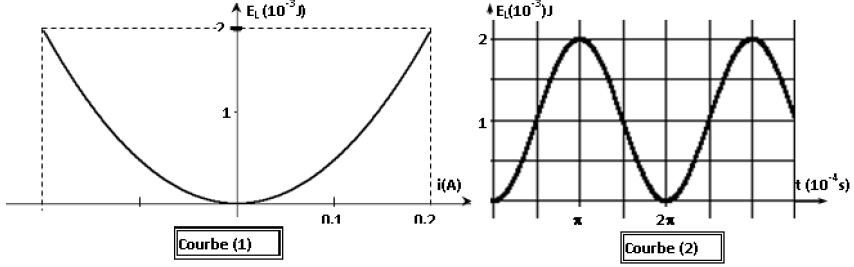
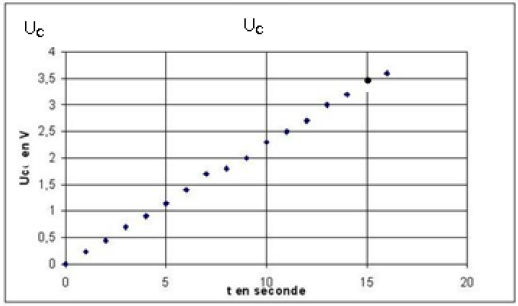
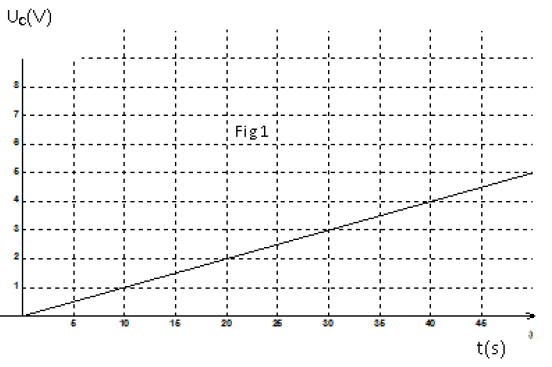
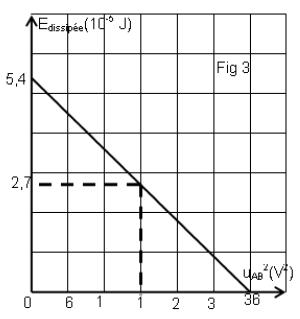
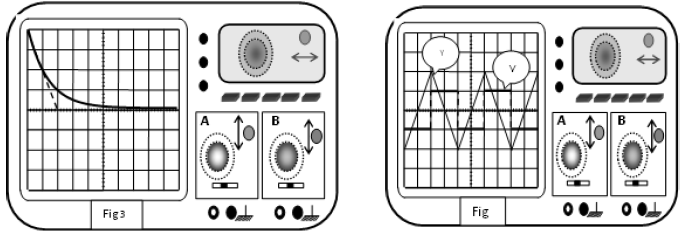
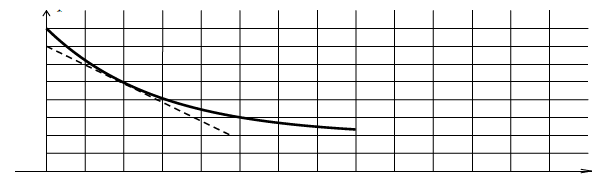
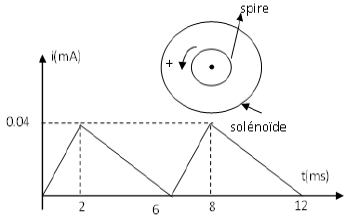
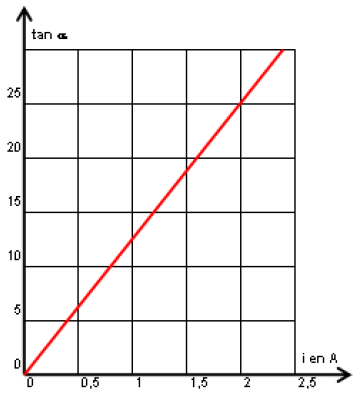
4) Une étude expérimentale a permis de tracer les courbes (1) et (2) (ci-dessous)
 
 
traduisant respectivement les variations de l'énergie magnétique $E_{L}$ en fonction de $i$ et en fonction du temps.
 
a) En exploitant la courbe (1), déduire les valeurs de $L$ et de $E_{0}.$
 
b) En exploitant la courbe (2), déduire la valeur de $T_{0}.$
 
5) Déterminer alors $C$, $Q_{0}$ et $U_{0}.$

Exercice 2

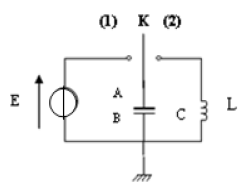
Avec un générateur de tension continue, de $f.e.m.$ 
 
$E_{0}$ constante et de résistance interne nulle, un condensateur de capacité $C$ et une bobine d'inductance $L$ et de résistance négligeable, on réalise le circuit de la :
 
A. L'interrupteur $K$ est dans la position (1)
 
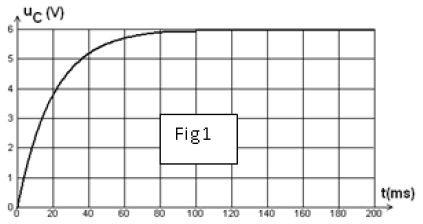
1) Quel est le phénomène observé ?
 
2) Donner l'allure de la courbe de variation de la tension aux bornes du condensateur en fonction du temps.
 
B. L'interrupteur $K$ est basculé dans la position (2) :
 
1) a) Établir l'équation différentielle qui régit les oscillations de la charge $q(t).$
 
b) Montrer que $q(t)=Q_{m}\sin\left(\omega_{0}t+\phi_{q}\right)$ peut être une solution de l'équation différentielle précédente. 
 
Donner l'expression de $\omega_{0}.$
 
2) a) Montrer que le circuit $(L\;,\ C)$ est conservatif et que son énergie totale est $E=\dfrac{1}{2C}Q_{m}^{2}.$
 
b) Montrer que l'énergie électrique emmagasinée dans le condensateur en fonction de $i^{2}$ est de la forme $E_{e}=\dfrac{1}{2C}Q_{m}^{2}-\dfrac{1}{2}L\cdot i^{2}.$
 
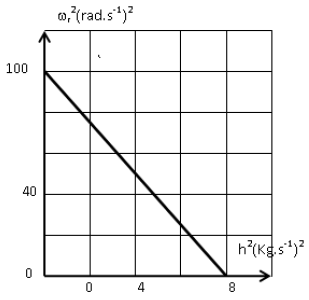
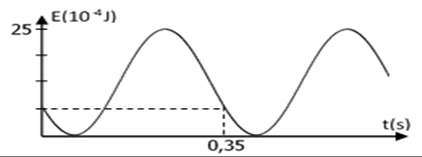
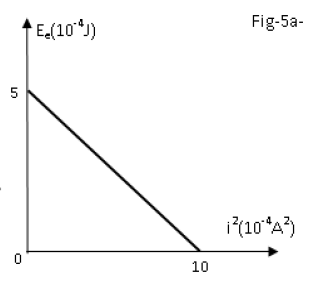
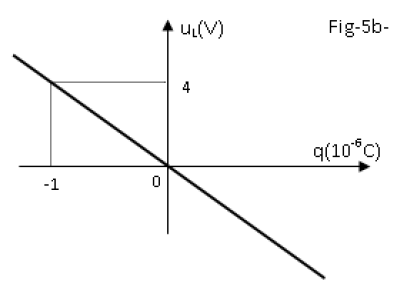
c) L'étude expérimentale a permis de tracer les courbes de la figure-5-,
 
 
donnant les variations de l'énergie électrostatique $E_{e}$ du condensateur en fonction de l'intensité $i$ du courant (fig-5a) 
 
 
et de la tension $u_{L}$ aux bornes de la bobine en fonction de la charge $q.$ (fig-5b).
 
 
Justifier théoriquement l'allure de la courbe figure-5b en établissant la relation entre $u_{L}$ et $q.$
 
3) En exploitant ces deux courbes, déterminer :
 
a) L'inductance $L$ de la bobine.
 
b) La capacité $C$ du condensateur.
 
c) La pulsation propre $\omega_{0}$ du circuit.
 
d) La charge maximale $Q_{m}.$
 
e) En déduire la $f.e.m$ du générateur.

Exercice 3

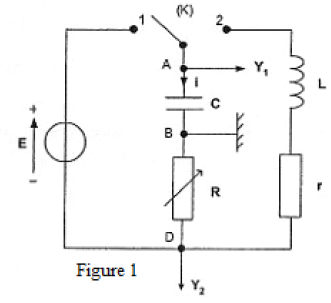
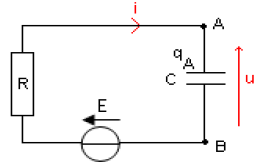
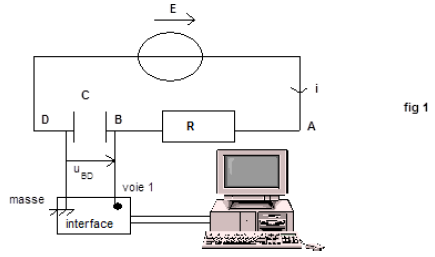
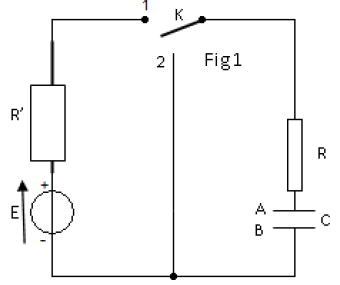
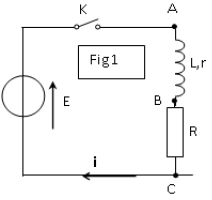
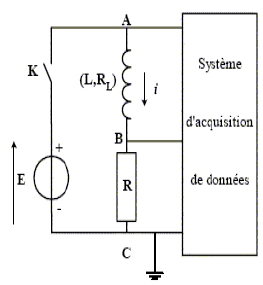
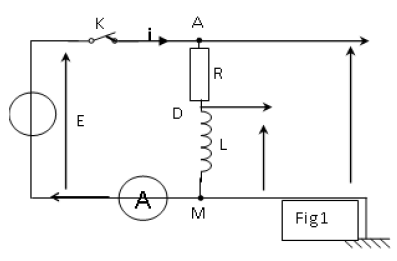
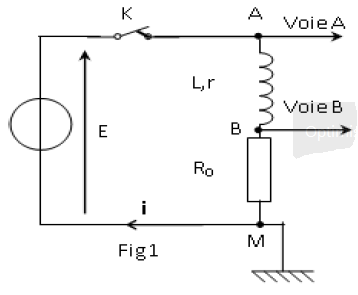
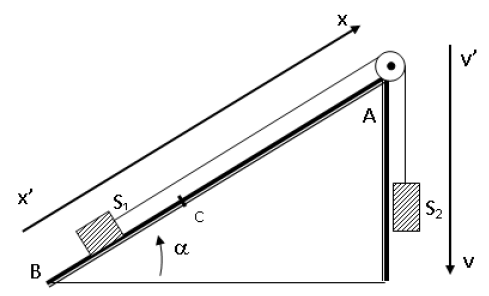
Au cours d'une séance de travaux pratiques, un élève réalise le circuit schématisé ci-dessous (figure 1).
 
 
Ce circuit est constitué des éléments suivants : un générateur délivrant une tension continue constante de valeur $E=4.0V$ ; une résistance $R$ réglable ; un condensateur de capacité $C=2.0\mu F$ ; une bobine d'inductance $L$ et de résistance $r.$
 
Un commutateur $(K)$ permet de relier le dipôle $(RC)$ soit au générateur, soit à la bobine.
 
L'entrée $Y_{1}$ d'une interface, reliée à un ordinateur, est connectée à la borne $A$ ; l'autre entrée $Y_{2}$ est connectée à la borne $D.$ 
 
La masse de l'interface est connectée à la borne $B.$
 
Les entrées $Y_{1}$, $Y_{2}$ et la masse de l'interface sont équivalentes respectivement aux entrées $Y_{1}$, $Y_{2}$ et à la masse d'un oscilloscope.
 
Étude énergétique du condensateur
 
Au cours de cette question, on étudie la charge du condensateur. 
 
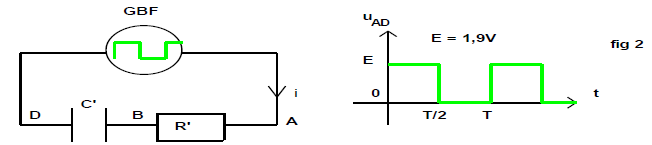
À l'instant de date $t=0s$, le condensateur est déchargé et on bascule le commutateur en position 1.
 
1.1 Représenter, sur la figure 1, par des flèches : la tension $u_{DB}(t)$ aux bornes de la résistance ; la tension $u_{AB}(t)$ aux bornes du condensateur.
 
1.2 Donner, en le justifiant, le signe de la charge $q$ portée par l'armature $A$ du condensateur au cours de sa charge et la relation existant entre la charge $q$ et la tension $U_{AB}.$ 
 
En tenant compte de l'orientation du circuit, donner la relation vérifiée à chaque instant par l'intensité $i(t)$ du courant et la charge $q(t).$
 
A partir des expressions des tensions aux bornes des trois dipôles, établir l'équation différentielle vérifiée par $u_{AB}(t).$ 
 
Donner l'expression de $u_{AB}(t)$ solution de cette équation différentielle en fonction de $E$, $R$, $C$ et $t$
 
1.3 Donner en fonction de $u_{AB}(t)$ l'expression littérale de l'énergie électrique $E_{e}$ emmagasinée par le condensateur. 
 
En déduire l'expression littérale $E_{e\;,\ max}$ de sa valeur maximale et calculer sa valeur.
 
2. Étude énergétique du circuit $RLC$
 
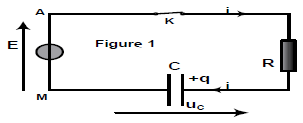
2.1 Une fois le condensateur chargé, l'élève bascule rapidement le commutateur $(K)$ de la position 1 à la position 2 : il prend l'instant du basculement comme nouvelle origine des dates. 
 
Le condensateur se décharge alors dans la bobine. 
 
L'acquisition informatisée des tensions permet de visualiser l'évolution des tensions $u_{AB}(t)$ et $u_{DB}(t)$ en fonction du temps. 
 
Après transfert des données vers un tableur-grapheur, l'élève souhaite étudier l'évolution des différentes énergies au cours du temps.
 
2.1 a) Exprimer littéralement, en fonction de $i(t)$, l'énergie magnétique $E_{m}$ emmagasinée dans la bobine.
 
À partir de l'une des tensions enregistrées $u_{AB}(t)$ et $u_{DB}(t)$, donner l'expression de l'intensité instantanée $i(t)$
 
2.1 b) En déduire l'expression de l'énergie magnétique emmagasinée dans la bobine en fonction de l'une des tensions enregistrées.
 
2.1 c) En déduire l'expression de l'énergie totale $E_{T}$ du circuit en fonction des tensions $u_{AB}(t)$ et $u_{DB}(t).$
 
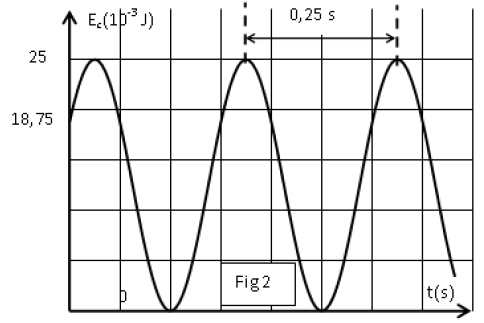
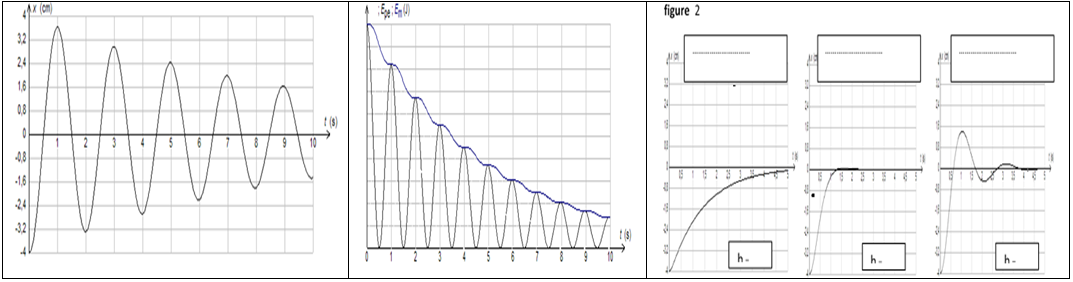
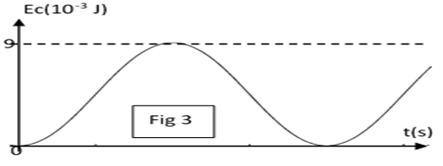
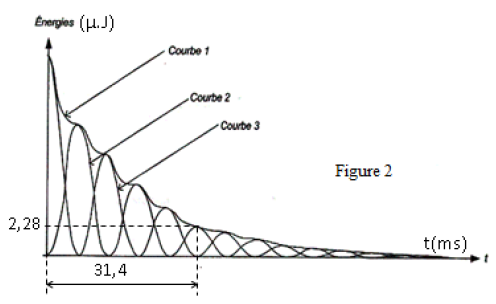
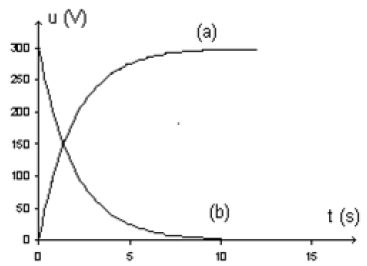
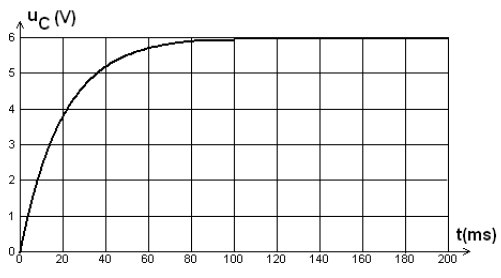
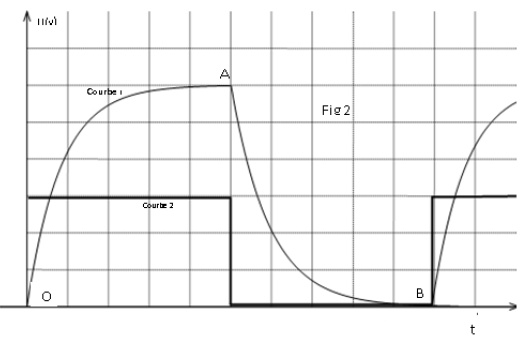
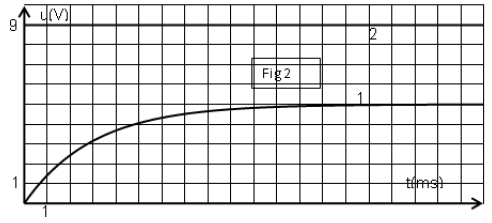
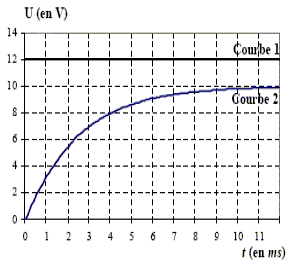
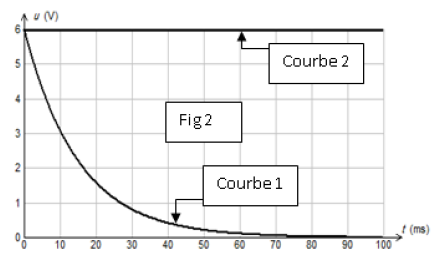
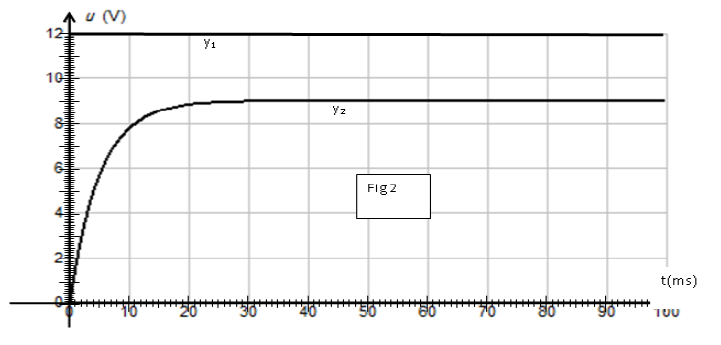
2.2 À partir du tableur-grapheur, l'élève obtient le graphe (figure 2) 
 
 
qui montre l'évolution, en fonction du temps, des trois énergies : $E_{e}$ énergie électrique, $E_{m}$, énergie magnétique et $E_{T}$ énergie totale.
 
2.2 a) Identifier chaque courbe en justifiant. 
 
Quel phénomène explique la décroissance de la courbe 1 ?
 
2.2 b) Montrer les transformations mutuelles de $E_{e}$ et de $E_{m}.$
 
2.2 c) Déterminer graphiquement :
 
$-\ $ La pseudo période $T.$
 
$-\ $ L'énergie dissipée par effet joule à la date $t=31.4\,ms.$
 
2.2 d) Pour réduire l'énergie dissipée par effet joule pendant chaque pseudopériode dans le circuit faut-il augmenter ou diminuer $R.$ 
 
Justifier.

Exercice 4

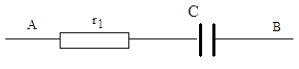
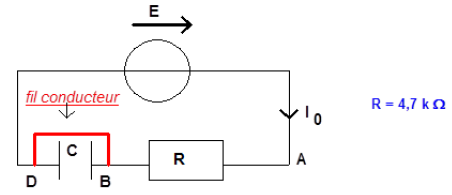
On considère le dipôle suivant, constitué d'un conducteur ohmique de résistance $r_{1}=100\Omega$ et d'un condensateur de capacité inconnue $C$ :
 
 
1) Pour mesurer son impédance, on applique à ce dipôle une tension sinusoïdale de fréquence $50\,Hz.$ 
 
On relève les valeurs efficaces de l'intensité $i_{AB}$ et de la tension $u_{AB}$ :
 
on trouve $I_{AB}= 9.40\,mA$ et $U_{AB}=6.0V.$
 
Calculer l'impédance $Z$ du dipôle $AB$ ; en déduire la capacité $C$ du condensateur (on pourra utiliser, en les adaptant, les formules rappelées en fin d'exercice au cas étudié ici).
 
2) Dans une autre expérience, on associe en série le dipôle $AB$ à une bobine de résistance $r=10\Omega$ et d'inductance $L$ variable. 
 
On maintient entre les bornes de l'ensemble une tension sinusoïdale de valeur efficace constante $6\,V$ et de fréquence $100\,Hz.$ (différente de celle du 1)
 
Quand $L$ varie, l'intensité efficace $I$ passe par un maximum pour $L=0.5\,H.$
 
Calculer à nouveau la capacité $C$ du condensateur et la valeur maximale de l'intensité efficace $I.$
 
3) On conserve le montage de la question précédente (conducteur ohmique, condensateur et bobine associés en série), mais on fait varier l'inductance de la bobine ; la nouvelle valeur est $L'=0.33\,H.$ 
 
La tension d'alimentation reste inchangée $(6\,V\ -\ 100\,Hz).$
 
3.1 Calculer l'impédance $Z'$ du montage, puis l'intensité efficace $I'$ du courant qui circule.
 
3.2 Déterminer le déphasage que présente la tension $u$ par rapport à l'intensité $i$ prise comme référence.
 
Donner les expressions de $i$ et $u.$
 
3.3 On dispose d'un oscillographe bicourbe. 
 
On envoie sur la voie $A$ la tension aux bornes du conducteur ohmique de résistance $r_{1}$ et sur la voie $B$ la tension aux bornes de l'ensemble du montage.
 
Représenter les deux courbes que l'on observe sur les voies $A$ et $B$ de l'oscillographe (on se limitera à représenter une période) :
 
le balayage est réglé sur $1\,ms/cm$, la sensibilité verticale vaut $2\,V/cm.$
 
Que peut-on vérifier grâce à cette observation ?

Exercice 5

On désire mesurer la résistance interne $R$ et l'inductance $L$ d'une bobine réelle de deux façons différentes.
 
Partie A Dans un premier temps, la bobine est alimentée en régime continu. 
 
Lorsque la tension à ses bornes vaut $U_{1}=10\,V$, l'intensité du courant qui la traverse vaut $I_{1}=0.2\,A.$
 
Dans un deuxième temps, la bobine est alimentée par un générateur basse fréquence délivrant une tension alternative sinusoïdale de fréquence $f=200\,Hz$, de valeur efficace $U=5\,V$ ; l'intensité efficace est alors $I=10\,mA.$
 
a) Calculer la valeur de $R.$
 
b) Calculer l'impédance $Z_{L}$ de la bobine réelle
 
c) En déduire la valeur de l'inductance $L.$
 
Partie B Ces résultats vont être vérifiés par une seconde méthode.
 
On réalise un dipôle $AB$ constitué par l'association série de la bobine réelle et d'un condensateur de capacité $C=1\mu F.$
 
La bobine sera assimilée à un résistor $R$ en série avec une bobine parfaite d'inductance $L.$
 
 
Le voltmètre nous indique la valeur efficace de la tension d'alimentation ; elle sera maintenue constante et vaut $U=5\,V.$
 
L'ampèremètre de résistance interne nulle nous indique la valeur de l'intensité efficace correspondante.
 
1) Donner l'expression littérale de l'impédance totale du circuit $AB.$
 
2) Pour $f=f_{0}=252\,Hz$, la valeur de l'intensité efficace passe par une valeur maximale $I_{0}=0.1\,A.$
 
a) Comment appelle-t-on ce phénomène ?
 
b) Que vaut l'impédance totale du circuit à $f_{0}$ ?
 
c) Calculer $R$ et $L$
 
d) Quelle est dans ces conditions la valeur de la tension efficace $U_{C}$ aux bornes du condensateur ? 
 
Comparer les valeurs efficaces de la tension d'alimentation $U$ et de la tension $U_{C}$ : commenter.
 
3) On se place à présent à $f_{1}=200\,Hz.$
 
a) Calculer la valeur de l'impédance totale du circuit.
 
b) En déduire la valeur de l'intensité efficace $I.$
 
c) Calculer le déphasage $\varphi$ de la tension instantanée $u(t)$ par rapport à l'intensité $i(t).$ 
 
Conclure quant au caractère inductif ou capacitif du dipôle $AB$ à la fréquence $f_{1}.$
 
d) Donner les expressions de $u(t)$ et de $i(t).$ 
 
On prendra $i(t)=I\sqrt{2}\sin(\omega\,t).$

Exercice 6 : Circuit $R\;,\ L\;,\ C$ Résonance d'intensité

Un circuit comprenant une résistance $R$, une inductance pure $L$, un condensateur $C$ montés en série, est alimenté sous une tension alternative sinusoïdale, de valeur efficace $U$ de fréquence réglable.
 
Données :
 
$U=2.00\,V$ 
 
$R=14.0\Omega$ 
 
$L=69.6\,mH$ 
 
$C=10.0\mu F$
 
1.
1.1 Pour une pulsation $\omega$ correspondant à une fréquence $f$, exprimer l'impédance $Z$ du circuit, l'intensité efficace $I$ du courant et le déphasage $\varphi_{u/i}$ de la tension d'alimentation par rapport au courant.
 
Calculer $Z$, $I$ et  $\varphi_{u/i}$ si $f=175\,Hz.$
 
1.2 Donner les expressions de $u(t)$ et de $i(t)$ ; on prendra $i$ comme référence pour la phase.
 
2. La valeur efficace $U$ de la tension d'alimentation est maintenue constante et égale à $2.00\,V.$
 
Pour des fréquences variant de $90$ à $300\;Hz$, on relève les valeurs correspondantes de l'intensité efficace du courant :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline f(Hz)&90&120&150&160&170&180&185&190&195&200&210&250&300\\ \hline I(mA)&14.9&22.8&38.5&60.4&83.2&116.3&132.7&142.5&141.7&135.4&93.5&40.9&25.7\\ \hline \end{array}$$
 
2.1
2.1 a) Tracer la courbe représentant $I$ en fonction de $f$, sur papier millimétré avec les échelles suivantes : $1\,cm$ pour $20\,Hz$ et $1\,cm$ pour $10\,mA.$ 
 
On portera un soin tout particulier à cette représentation graphique.
 
2.1 b) Déterminer graphiquement la fréquence $f_{0}$ et l'intensité efficace $I_{0}$ du courant correspondant à la résonance.
 
2.2 Calculer ces valeurs et comparer à celles déterminées graphiquement.
 
3.
3.1
3.1 a) Pour la fréquence de résonance $f_{0}$, donner l'expression littérale de la tension efficace $U_{C}$ aux bornes du condensateur.
 
3.1 b) Montrer que cette tension peut se mettre sous la forme $U_{C}=Q\times U$ où $Q$ est indépendant de $U.$
 
3.1 c) $Q$ est appelé le coefficient de surtension. 
 
Indiquer un autre nom possible pour $Q.$
 
3.2
3.2 a) Calculer numériquement $Q$ et $U_{C}.$
 
3.2 b) Indiquer l'inconvénient que peut présenter le phénomène de surtension.
 
4. On appelle bande passante en fréquence l'intervalle de fréquence pour lequel l'intensité efficace $I$ est supérieure ou égale à $\dfrac{I_{0}}{\sqrt{2}}.$
 
4.1 Déterminer graphiquement la bande passante $B=f_{2}-f_{1}\;,\ f_{2}\text{ et }f_{1}$ étant les fréquences pour lesquelles $I=\dfrac{I_{0}}{\sqrt{2}}$
 
4.2 Comparer cette largeur de la bande ainsi déterminée à celle calculée à partir de la relation $B=\dfrac{f_{0}}{Q}$

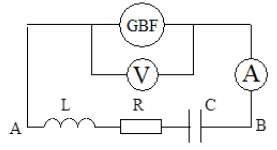
Exercice 7

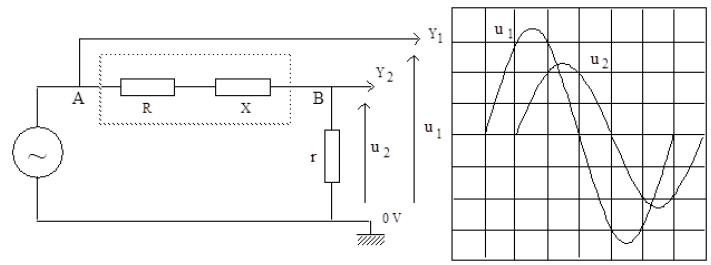
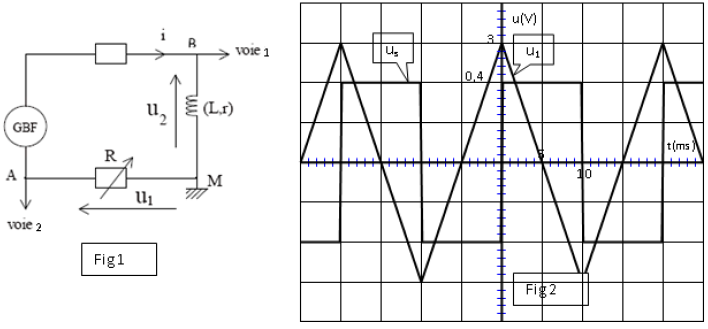
On réalise un circuit électrique schématisé sur la figure -1- et comprenant un générateur $B.F.$
 
 
délivrant une tension sinusoïdale $u(t)=U_{m}\sin(2\pi\;f\;t)$ d'amplitude $U_{m}$ constante de fréquence $f$ variable, aux bornes duquel sont disposés en série le condensateur de capacité $C=1\mu F$, une bobine de résistance $r$ et d'inductance $L=0.01H$ et un résistor de résistance $R.$
 
On se propose de visualiser sur l'écran d'un oscilloscope à deux voies :
 
$-\ $ la tension $u(t)\ \longrightarrow\ voie(1).$
 
$-\ $ la tension $u_{R}t\ \longrightarrow\ voie(1).$
 
1) Établir à l'aide d'un tracé clair les connexions nécessaires entre le circuit électrique de la figure-1- et l'oscilloscope.
 
2) Établir l'équation reliant $i$, sa dérivée première $\dfrac{\mathrm{d}i}{\mathrm{d}t}$ et sa primitive $\int\,i\mathrm{d}t.$
 
Soit $i(t)=I_{m}\sin(2\pi\;f\;t+\varphi_{i})$ la solution de cette équation .
 
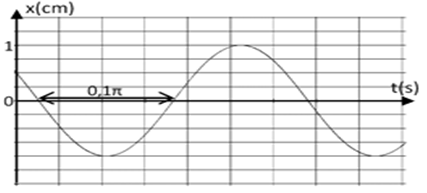
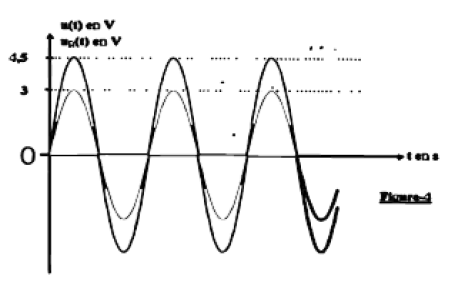
3) a) Expérience $n^{\circ}1$
 
On ajuste la fréquence $f$ à la valeur $f_{0}$ correspondant à la fréquence propre du dipôle $(L\;,\ C).$
 
On obtient les diagrammes de la figure-2-.
 
$-\ $ Montrer que, parmi les deux signaux qui constituent cette figure, celui ayant l'amplitude la plus élevée correspond à la tension $u(t).$
 
$-\ $ Établir que $\dfrac{R}{R+r}=\dfrac{2}{3}$
 
 
b) Expérience $n^{\circ}2$
 
A partir de cette valeur $f_{0}$, on fait varier la fréquence $f$ de la tension excitatrice $u(t)$ jusqu'à rendre cette dernière déphasée de $\dfrac{\pi}{6}$ par rapport au courant $i(t).$ 
 
La nouvelle de la fréquence est alors $f_{1}=1524\,Hz.$
 
$-\ $ Dire, en le justifiant, si le circuit est inductif ou capacitif.
 
$-\ $ Faire la construction de Fresnel en tenant compte des données de cette expérience $n^{\circ}2$ et montrer que $R+r=\sqrt{3}\left(\dfrac{1}{2\pi\;f_{1}\cdot C}-2\pi\;f_{1}\cdot L\right).$
 
$-\ $ Calculer $R$ et $r.$
 
c) Déterminer le facteur de qualité $Q$ de cet oscillateur

Exercice 8

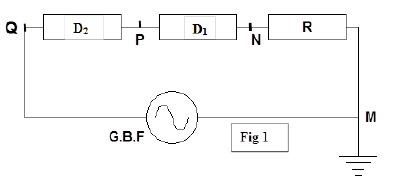
Deux dipôles $D_{1}$ et $D_{2}$ inconnus, mais chacun d'eux peut être : un résistor de résistance $R'$.
 
Une inductance pure $L$ ou un condensateur parfait de capacité $C.$
 
On veut identifier $D_{1}$ et $D_{2}$ et déterminer ses grandeurs caractéristiques, on dispose alors d'un résistor de résistance $R=155.5\Omega$, d'un oscilloscope bicourbe et d'un générateur basse fréquence. 
 
Pour atteindre cet objectif, on a réalisé le montage de la figure 1. 
 
 
Le circuit est alimenté par une tension alternative sinusoïdale $u(t)=U_{m}\sin(2\pi\;N\,t).$
 
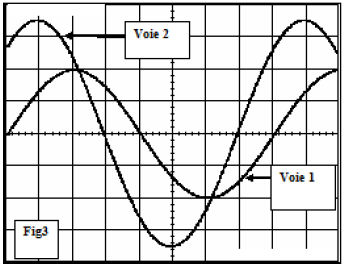
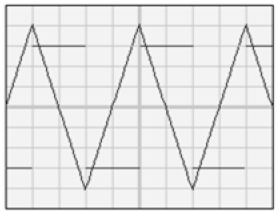
$-\ $ Dans une première expérience on a visualisé la tension $u_{NM}$ sur la voie 2 de l'oscilloscope et la tension $u_{PM}$ sur la voie 1 on a obtenu les courbes de la figure 2.
 
 
$-\ $ Au cours d'une deuxième expérience on a visualisé la tension $u_{NM}$ sur la voie 2 de l'oscilloscope et la tension $u_{QM}$ sur la voie 1 on a obtenu les courbes de la figure 3.
 
 
On donne :
 
Sensibilité horizontale : $1\,ms$ par division.
 
Sensibilité verticale Voie 1 : $5\,V$ par division
                      Voie 2 : $2\,V$ par division
 
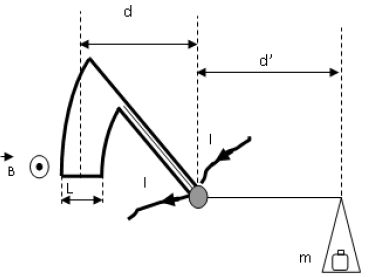
1) a) A partir de l'oscillogramme de la figure 2, Montrer que le dipôle $D_{1}$ est une inductance.
 
b) Étudier l'oscillogramme de la figure 3 et montrer que le dipôle $D_{2}$ est un condensateur.
 
2) A partir de l'oscillogramme de la figure 3, déterminer :
 
a) La fréquence $N$ et la valeur efficace $U$ de la tension $u(t)$ délivrée par le générateur.
 
b) L'intensité efficace $I$ du courant qui traverse le circuit (le résultat doit être donné avec trois chiffres après la virgule). 
 
En déduire l'impédance $Z$ du circuit.
 
c) Le déphasage $\Delta\varphi$ de la tension aux bornes de tout le circuit par rapport à l'intensité du courant qui le traverse. 
 
Quelle est la nature du circuit ?
 
d) Écrire l'expression de $i(t).$
 
3) L'équation différentielle régissant les variations de l'intensité du courant dans le circuit est $\dfrac{L\;\mathrm{d}i}{\mathrm{d}t}+Ri+\dfrac{1}{c}\int\,i\mathrm{d}t=u.$
 
a) Faire correspondre à chaque fonction un vecteur de Fresnel. 
 
Sachant que la valeur de l'inductance est $L=0.2H$, Faire la construction de la figure 4 page 4 $(1V$ est représenté par $1\,cm).$
 
b) Déduire la valeur de la capacité $C$ du condensateur.
 
4) On règle la fréquence du générateur $B.F$ à une valeur $N_{1}$ de manière que la tension efficace $U_{QN}=0.$
 
a) Montrer que le circuit est le siège d'une résonance d'intensité. 
 
En déduire la valeur de la fréquence $N_{1}.$
 
b) Calculer dans ces conditions le rapport $\dfrac{U_{QP}}{U_{QM}}.$ 
 
Que représente ce rapport.
 
5) La fréquence de la tension excitatrice est réglée à une valeur quelconque $N_{2}.$
 
a) Montrer que la puissance électrique moyenne de ce circuit s'écrit sous la forme $P=\dfrac{RU^{2}}{\left(R^{2}+A^{2}\right)}.$ 
 
On donnera l'expression de $A$ en fonction de $\omega$ et des grandeurs caractéristiques de $D_{1}$ et de $D_{2}.$
 
b) Pour quelle valeur de $R$ cette puissance moyenne est maximale ?
 
c) Montrer que pour cette valeur de $R$, le déphasage courant-tension est indépendant de $\omega$, de $L$ et de $C$ et qu'il est toujours égal à $±\dfrac{\pi}{4}rad$

Exercice 9

Un dipôle $AB$ constitué d'une résistance $R$ et d'une réactance $X$ est branché en série avec une résistance pure $r=50\Omega.$ 
 
Un générateur de tension sinusoïdale, de fréquence $f=50\,Hz$, alimente le circuit.
 
 
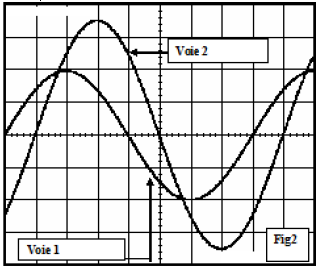
Les tensions sinusoïdales $u_{1}$ et $u_{2}$ sont observées sur l'écran d'un oscillographe bicourbe.
 
Les sensibilités des voies $Y_{1}$ et $Y_{2}$ sont respectivement de $1\,V/carreau$ et de $5\,V/carreau.$
 
L'observation de l'écran fournit une amplitude de $3.4$ carreaux pour $u_{1}$ et $2.3$ carreaux pour $u_{2}.$
 
Le décalage dans le temps des deux courbes permet de mesurer le déphasage $\varphi$ de $u_{1}$ par rapport à $u_{2}.$
 
1) Calculer les valeurs maximales des tensions $u_{1}$ et $u_{2}$ et les valeurs efficaces correspondantes.
 
2) Considérant la tension de référence $u_{2}$ en phase avec le courant $i$, déduire le sens du déphasage $\varphi$ de $u_{1}$ par rapport à $u_{2}.$
 
Quelle est la nature de la réactance $X$ (inductive ou capacitive) à la fréquence considérée ?
 
3) Calculer la valeur maximale et la valeur efficace du courant $i$ traversant le circuit.
 
4) Déterminer le déphasage de $u_{1}$ par rapport au courant.
 
5) Calculer l'impédance totale $Z$ du circuit série formé par le dipôle $AB$ et $r.$
 
6) Calculer la résistance $R$ constitutive du dipôle $AB$ [on rappelle que $|\cos\varphi|=\dfrac{R_{(totale)}}{Z_{(totale)}}$
 
7) Calculer la réactance $X$ et la valeur de l'inductance $L$ constitutive du dipôle $AB.$
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Étude du dipôle RC - Ts

Classe: 
Terminale
 

Exercice 1

On veut déterminer la capacité $C$ d'un condensateur, pour cela on réalise sa charge avec un générateur de courant. 
 
Ce générateur débite un courant d'intensité $I=0.5\,mA.$ 
 
On réalise la saisie automatique de la tension $U_{C}$ aux bornes du condensateur en fonction du temps. 
 
Le montage utilisé est schématisé ci-dessous :
 
 
1) Refaire le schéma du montage ; représenter $U_{C}$, $q$ $(q>0)$, la voie $Y$ et la masse de l'oscilloscope afin que l'on puisse visualiser $U_{C}.$
 
2) A l'instant $t=0$ on ferme l'interrupteur $K.$ 
 
Établir la relation entre $I$, $C$, $U_{C}$ et $t.$
 
3) On obtient la courbe $U_{C}(t)$ : (voir document ci-dessous). 
 
 
A l'aide de la courbe, déterminer la valeur de la capacité $C$ du condensateur.
 
4) Afin de ne pas détériorer le condensateur, la durée de charge ne doit pas dépasser $t_{max}=2\,min.$
 
a) Calculer la tension de claquage du condensateur.
 
b) Déduire l'énergie électrique maximale emmagasinée par le condensateur.

Exercice 2

Le montage représenté ci-dessous permet de charger et de décharger un condensateur dans une résistance $R.$
 
 
1) a) Pour chacune de ces deux opérations, quelle doit être la position de l'interrupteur ?
 
1) b) Des deux graphes (fig 1 et fig 2) proposés ci-dessous, lequel correspond à la charge de ce condensateur ? 
 
 
 
Justifier.
 
2) Le générateur de courant permet une charge, à intensité constante, d'un condensateur. 
 
La charge dure $40\,s$ et l'intensité du courant a pour valeur $1\mu A.$
 
2) a) Calculer la charge du condensateur à la date $40\,s.$
 
2) b) Quelle est la valeur de l'énergie emmagasinée par le condensateur à cette date ?
 
2) c) Quelle est la capacité du condensateur ?
 
3) Sachant que ce condensateur est plan et que l'aire des deux surfaces communes en regard est $S=0.1\,m^{2}$ et que l'épaisseur du diélectrique qui se trouve entre les deux plaques est $e=0.02\,mm.$
 
a) déterminer la permittivité électrique absolue $\epsilon$ du diélectrique de ce condensateur.
 
b) Déduire la permittivité relative $\epsilon_{r}$ du diélectrique. 
 
On donne $\epsilon_{0}=8.85\cdot10^{-12}u.s.i$

Exercice 3

Le circuit électrique représenté par la figure ci-dessous (fig 2) est constitué des éléments suivants :
 
 
$-\ $ Un générateur de tension idéale de $f.e.m$ $E.$
 
$-\ $ Deux conducteurs ohmiques de résistances $R_{1}$ et $R_{2}.$
 
$-\ $ Un condensateur de capacité $C$ initialement déchargé.
 
$-\ $ Un commutateur $K.$
 
I. A l'instant $t=0$, on place le commutateur $K$ dans la position 1. 
 
Un système d'acquisition approprié permet d'obtenir les courbes de variation de la charge $q(t)$ du condensateur et la tension $u_{R_{1}}(t)$ aux bornes du résistor $R_{1}.$ (voir fig 3 et fig 4).
 
 
1) a) Préciser, en le justifiant, le graphe correspondant à la charge $q=f(t)$ et celui correspondant à la tension $u_{R_{1}}=g(t).$
 
b) Établir, à un instant de date $t$ quelconque la relation entre $q$, $u_{R_{1}}$, $E$ et $C.$
 
c) Montrer qu'à la date $t=0$, la tension $u_{R_{1}}$ est égale à $E.$ 
 
En déduire sa valeur $($pour le graphe de $u_{R_{1}}(t)$ : $1$ carreau$\ \longrightarrow\ 2\,V).$
 
d) A partir du graphe de $q(t)$, prélever la valeur de la charge électrique maximale $Q_{max}$ du condensateur $(1$ carreau$\ \longrightarrow\ 2\cdot10^{-4}C).$
 
2) a) Définir la constante de temps $\tau$ d'un dipôle $RC.$ 
 
Montrer que $\tau$ est un temps.
 
b) Montrer que l'équation différentielle régissant les variations de $u_{R_{1}}$ au cours du temps peut s'écrire sous la forme $$\tau_{1}\dfrac{\mathrm{d}u_{R_{1}}}{\mathrm{d}t}+u_{R_{1}}=0\text{ avec }\tau_{1}=R_{1}C.$$
 
c) La solution générale de cette équation est de la forme : $u_{R_{1}}=A\mathrm{e_{-\alpha\;t}}.$ 
 
Déterminer $A$ et $\alpha.$
 
d) Montrer que lorsque le condensateur est complètement chargé, sa tension est égale à $E.$
 
Déduire la valeur de la capacité $C.$
 
3) a) Déterminer graphiquement $\tau_{1}.$ 
 
Préciser la méthode utilisée.
 
b) Calculer la valeur de $R_{1}.$
 
c) Calculer l'énergie électrique emmagasinée dans le condensateur lorsque $u_{R_{1}}=u_{C}.$
 
II. Lorsque le condensateur est complètement chargé, on bascule le commutateur $K$ à la position $2$ à un instant choisi comme nouvelle origine des dates.
 
1) a) Écrire la loi des mailles correspondante.
 
b) Montrer qu'à la date $t=0$, la tension aux bornes du résistor $R_{2}$ est $u_{R_{2}}=-E.$
 
2) La tension aux bornes du résistor $R_{2}$ est donnée par l'expression $u_{R_{2}}=-E\cdot \mathrm{e^{-t/\tau_{2}}}$ avec $\tau_{2}=R_{2}C.$
 
a) Sachant qu'à la date $t_{2}=4\cdot10^{-2}s$, la charge du condensateur est $q=3.7\cdot10^{-4}C.$ 
 
Calculer $R_{2}.$
 
b) Représenter sur le même graphe l'allure de la courbe représentant $q$ en fonction du temps au cours de la décharge. 
 
Même question pour la tension $u_{R_{2}}(t).$

Exercice 4

Au cours d'une séance de $TP$ on étudie la décharge d'un condensateur de capacité $C$ (préalablement chargé) à travers un dipôle ohmique de résistance $R.$ 
 
Un ordinateur muni d'une interface et d'un tableur a permis de tracer les courbes représentant l'évolution de la tension $u=u_{AB}$ et de l'intensité du courant dans le circuit (voir ci-dessous).
 
 
 
1) Établir la relation entre $i$ et $\dfrac{\mathrm{d}u}{\mathrm{d}t}.$
 
2) Donner, en justifiant la réponse, le signe de $q_{A}$ à l'instant $t=0.$
 
3) Indiquer, en justifiant les réponses, le sens réel du courant et le sens de déplacement des électrons.
 
4) Déterminer la valeur de la constante de temps $\tau$ du dipôle $RC.$
 
5) Déterminer les valeurs de $R$ et de $C.$

Exercice 5

On étudie le flash d'un appareil photographique jetable. 
 
Dans ce type d'appareil, une pile de $1.5V$ alimente un oscillateur. 
 
Un transformateur élève la tension qui, après avoir été redressée, permet de charger un condensateur. 
 
Une lampe témoin s'allume lorsque le flash est prêt à fonctionner. 
 
La décharge du condensateur dans une lampe à éclat engendre l'éclair.
 
Le condensateur utilisé porte les indications suivantes : $330\,V$ ; $160\mu F\pm;10\%.$ 
 
La durée minimale séparant deux déclenchements successifs du flash est de $10\,s.$
 
Pour vérifier la valeur de la capacité du condensateur, on réalise le montage schématisé ci-dessous.
 
 
Le condensateur, initialement déchargé, est alimenté à travers un dipôle ohmique de résistance $R=12.5k\Omega$ par une source idéale de tension appliquant une tension $E=300\,V.$
 
A l'aide d'un oscilloscope numérique, on visualise la tension $u_{C}$ aux bornes du condensateur ainsi que la tension $u_{R}$ aux bornes du dipôle ohmique. 
 
Ces courbes sont représentées ci-dessous.
 
 
1) Indiquer, sur le schéma du montage, le branchement permettant à un oscilloscope de tracer les courbes (a) et (b). 
 
On précisera sur le schéma les tensions effectivement mesurées.
 
2) Des tensions $u_{R}$ et $u_{C}$, quelle est celle qui permet de suivre l'évolution du courant (intensité) dans le circuit ? 
 
Justifier la réponse.
 
3) Quelle est des deux courbes (a) et (b) celle qui représente $u_{C}$ ? 
 
Justifier la réponse.
 
4) Montrer que le produit $R_{C}$ est homogène à une durée.
 
5) Montrer qu'une seule des équations différentielles suivantes est correcte.
$$(1)\quad R\dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+Cu_{R}=0\ ;$$
$$(2)\quad C\dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+Ru_{R}=0\ ;$$
$$(3)\quad RC\dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+u_{R}=0\ ;$$
$$(4)\quad \dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+RCu_{R}=0\ ;$$
 
6) La solution de l'équation différentielle vérifiée par la tension $u_{R}$ a pour expression : $u_{R}=E\mathrm{e^{-t/\tau}}$ avec $\tau=RC.$
 
Montrer que l'on peut écrire : $Ln(u_{R})=at+b.$ 
 
On exprimera $a$ et $b$ en fonction de $E$ et $\tau.$
 
7) La droite précédente est tracée par l'ordinateur (document ci-dessous). 
 
 
En déduire la valeur de la capacité $C$ du condensateur. 
 
Cette valeur est-elle en accord avec l'indication portée sur le condensateur ?

Exercice 6

1. On considère le circuit électrique ci-dessous comprenant un conducteur ohmique de résistance $R=4.7\,k\Omega$, un condensateur de capacité $C$ et une alimentation stabilisée de tension à vide $E.$ 
 
Un fil conducteur relie les bornes $B$ et $D$ du condensateur.
 
 
1.1 Que vaut la tension aux bornes du condensateur ?
 
1.2 Déterminer l'expression de l'intensité $I_{0}$ du courant dans le circuit en fonction de certains paramètres parmi les suivants $E$, $R$, $C.$
 
2. On se propose de suivre l'évolution de la tension $u_{BD}$ aux bornes du condensateur, au cours du temps.
 
Un ordinateur est relié au circuit électrique par l'intermédiaire d'une interface d'acquisition de données (voir figure 1)
 
 
A la date $t=0$, on enlève le fil conducteur aux bornes du condensateur. 
 
On enregistre alors la variation de la tension $u_{BD}$ aux bornes du condensateur au cours du temps. 
 
L'acquisition de mesures étant terminée, on trace le graphe d'équation $u_{BD}=f(t)$ (voir document 1).
 
2.1 Déterminer, à partir du document 1, la valeur de la tension $E.$
 
En déduire la valeur de l'intensité $I_{0}$ du courant dans le circuit à $t=0.$
 
2.2 Établir que l'équation différentielle d'évolution de la tension $u_{BD}$ au cours du temps est donnée par l'expression :
$$\boxed{\dfrac{\mathrm{d}u_{BD}}{\mathrm{d}t}+\dfrac{u_{BD}}{RC}=\dfrac{E}{RC}}$$
 
Vérifier à partir de l'équation différentielle que la constante de temps du circuit $\tau=RC$ est homogène à une durée.
 
2.3 A partir du coefficient directeur de la tangente $(T)$ à la courbe $u_{BD}=f(t)$ à l'instant de date $t=0$, déterminer la constante de temps du circuit. 
 
En déduire la valeur de la capacité $C$ du condensateur.
 
A partir du document 1, déterminer la durée au bout de laquelle on peut considérer que le condensateur est chargé. 
 
Comparer cette durée à la constante de temps $\tau$ du circuit.
 
3. On désire visualiser sur un oscilloscope l'évolution de la tension $u_{BD}$ aux bornes du condensateur lors de sa charge.
 
Le circuit électrique comprend maintenant un générateur basse fréquence $(GBF)$ délivrant une tension carrée $u_{AD}$, un condensateur de capacité $C'=10\,nF$ et un conducteur ohmique de résistance $R'=10\,k\Omega.$ (fig 2).
 
 
4. Indiquer, sur le circuit électrique de la figure 2, les branchements à réaliser pour visualiser sur la voie 1 de l'oscilloscope la tension délivrée par le générateur basse fréquence, et sur la voie 2 la tension aux bornes du condensateur.

Exercice 7

I. On se propose d'étudier l'évolution de la tension aux bornes d'un condensateur dans le but de déterminer la capacité du condensateur.
 
Un générateur de tension de force électromotrice $E$ alimente un conducteur ohmique de résistance $R=100\Omega$ et un condensateur de capacité $C$, associés en série (figure 1).
 
 
Un dispositif d'acquisition de données relié à un ordinateur permet de suivre l'évolution de la tension $u_{C}$ aux bornes du condensateur en fonction du temps.
 
À la date $t=0$, on ferme l'interrupteur $K$ et l'ordinateur enregistre la courbe $u_{C}=f(t).$
 
 
1) À l'aide de la courbe $u_{C}(t)$, déterminer la date $t$ à partir de laquelle on peut considérer que la tension $u_{C}$ est constante. 
 
Quel phénomène physique est mis en évidence par la portion de courbe située avant la date $t$ ?
 
2) Déterminer la valeur de $E.$ 
 
Expliquer.
 
3) Déterminer la valeur de la constante de temps $\tau$ du circuit.
 
4) En déduire une valeur approchée de $C.$
 
5) Évaluer, à partir de la figure ci-dessus, la durée $\Delta\;t$ nécessaire pour charger complètement le condensateur. 
 
Comparer $\Delta\;t$ à $\tau.$
 
6) Faut-il augmenter ou diminuer la valeur de $R$ pour charger plus rapidement le condensateur ? 
 
Justifier la réponse.
 
7) En respectant l'orientation d'intensité qui est indiquée sur la figure 1, établir l'équation différentielle vérifiée par la tension $u_{C}.$
 
8) Sachant que $u_{C}=E\left(1-\mathrm{e^{-t/RC}}\right)$ est solution de l'équation différentielle et en respectant l'orientation d'intensité qui est indiquée sur la figure 1, établir l'expression de $i(t).$ 
 
En déduire l'allure de la courbe $i=f(t).$

Exercice 8

On dispose au laboratoire d'un condensateur de capacité $C$ inconnue, pour déterminer expérimentalement la valeur de $C$, deux groupes d'élèves proposent deux solutions différentes.
 
I. Le premier groupe réalise un circuit électrique comportant :
 
$\ast\ $ Un générateur idéal de courant débitant un courant d'intensité constante $I=20\mu A.$
 
$\ast\ $ Un voltmètre.
 
$\ast\ $ Le condensateur de capacité $C$ inconnue.
 
$\ast\ $ Un conducteur ohmique de résistance $R$
 
$\ast\ $ Un interrupteur $K$ et un chronomètre.
 
A la date $t=0$, ils ferment l'interrupteur $K$ et mesurent à différentes dates la tension aux bornes du condensateur, ce qui leur a permis de tracer la courbe de variation de la tension $u_{c}$ aux bornes du condensateur en fonction du temps (figure 1 ).
 
 
1) Représenter le schéma du circuit en indiquant le branchement du voltmètre.
 
2) Établir l'expression de $u_{C}$ en fonction de $I$, $C$ et $t.$
 
3) Déterminer graphiquement la valeur de la capacité $C.$
 
Calculer à la date $t=20\,s$, l'énergie emmagasinée dans le condensateur.
 
II. Le deuxième groupe réalise un circuit électrique comportant :
 
$-\ $ Un générateur basse fréquence $G.B.F$ de signaux carrés, de fréquence $N$, fournissant alternativement une tension nulle ou positive $U_{m}$ (Tension créneaux).
 
$-\ $ Un oscilloscope bicourbe,
 
$-\ $ Le condensateur de capacité $C$ inconnue.
 
$-\ $ Un conducteur ohmique de résistance $R$ réglable et un interrupteur $K.$
 
1) Représenter le schéma du circuit en indiquant les branchements des fils de masse et les entrées $Y_{A}$ et $Y_{B}$ de l'oscilloscope nécessaire pour visualiser respectivement la tension fournie par le $G.B.F$ et la tension aux bornes du condensateur.
 
2) Avec $R=40\Omega$, on observe sur l'écran de l'oscillo les courbes de la figure 2.
 
Les réglages de l'oscilloscope indiquent Sensibilité verticales sur $Y_{A}$ : $2V\cdot div^{-1}$ et sur $Y_{B}$ : $1V\cdot div^{-1}.$
 
Sensibilité horizontale : $10\,ms\cdot div^{-1}.$
 
a) Identifier les courbes 1 et 2, interpréter le phénomène observé principalement, dans les zones $OA$ et $AB.$
 
b) Établir l'équation différentielle régissant les variations de $u_{C}$ dans la zone $OA.$ 
 
Donner l'expression de sa solution en fonction de $U_{m}$, $R$, $C$ et $t.$
 
c) Déterminer graphiquement
 
$-\ $ La période $T$ du $G.B.F$ et la tension maximale $U_{m}$ fournie.
 
Calculer la fréquence $N.$
 
$-\ $ la constante de temps $\tau.$ 
 
Déduire la valeur de la capacité $C$ du condensateur, la comparer à celle trouvée par le premier groupe.
 
d) Tracer sur le même graphe l'allure de la courbe de variation de la tension $u_{R}$ aux bornes du résistor en fonction du temps. 
 
Préciser sur le graphe les deux régimes.
 
3) On règle la résistance $R$ à la valeur $60\Omega.$
 
a) Calculer la nouvelle valeur de la constante de temps.
 
Tracer, sur le même graphe, l'allure de la courbe représentant $u_{C}$ en fonction du temps.
 
 

Exercice 9

I. Le condensateur de capacité $C$ utilisé dans le montage schématisé ci-dessous est alimenté par un générateur de tension supposé idéal délivrant entre ses bornes une tension $E=6V.$ 
 
 
Un conducteur ohmique a une résistance $R=300\Omega$ alors que l'autre sa résistance $R'$ est inconnue. 
 
Le condensateur étant initialement déchargé, le commutateur $K$ est placé sur la position $1$ à un instant pris comme origine de temps et à l'aide d'un ordinateur muni d'une interface on a pu suivre l'évolution de l'intensité de courant électrique dans le circuit voir figure 2 (page à compléter et à remettre avec la copie)
 
 
1) En désignant par $q$ la charge positive portée par l'armature $A$ du condensateur à une date $t.$ 
 
Indiquer sur le schéma le sens arbitraire positif du courant $i(t).$
 
2) En appliquant la loi des mailles, établir l'équation différentielle régissant les variations de l'intensité du courant $i(t).$
 
3) Cette équation différentielle admet pour solution : $i(t)=A\cdot\mathrm{e^{-\alpha\;t}}$ où $A$ et $\alpha$ sont deux constantes positives qu'on déterminera leurs expressions.
 
4) Déterminer l'expression de la tension aux bornes du condensateur $u_{AB}(t).$
 
5) En utilisant le graphe de $i(t)$, déterminer :
 
a) la valeur de la résistance $R'.$
 
b) la valeur de la constante de temps $\tau.$ 
 
Déduire la valeur de la capacité $C.$
 
II. Lorsque l'intensité de courant s'annule dans le circuit, on bascule le commutateur $K$ sur la position $2$ à une date considérée comme origine de temps alors qu'on a programmé l'ordinateur pour tracer la courbe d'évolution de l'énergie dissipée dans le résistor $R$ en fonction de $u_{AB}^{2}.$ 
 
La courbe obtenue est donnée par la figure 3
 
 
1) En appliquant la loi des mailles, établir l'équation différentielle régissant les variations de la tension $u_{AB}(t).$
 
2) La solution de l'équation différentielle précédente est $u_{AB}(t)=E\cdot\mathrm{e^{-t/\tau}}.$
 
3) Trouver l'expression de l'intensité du courant et déduire le sens du courant réel.
 
4) Montrer que l'énergie dissipée par effet joule dans le résistor $R$ s'écrit sous la forme :
$$E_{\text{dissipée}}=-\dfrac{1}{2}C\cdot u_{AB}^{2}+\dfrac{1}{2}C\cdot E^{2}$$
 
5) En utilisant le graphe de la figure 3 :
 
a) Retrouver la valeur de la capacité du condensateur.
 
b) Déterminer l'instant $t$ pour lequel l'énergie dissipée est égale à l'énergie emmagasinée dans le condensateur
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Interférences lumineuses

Exercice1
Deux fentes $F_{1}$ et $F_{2}$ distantes de $a=2mm$ émettent de la lumière provenant d'une
même fente $F$ Elles produisent un système d'interférences lumineuses sur un écran placé à la
distance $D=2m$ des fentes. La lumière de la source $F$ contient deux radiations
monochromatiques, de longueur d‟onde $λ_{1}=0,60µm$ et $λ_{2}=0,48µm$. L'interfrange $i$ (distance
séparant les milieux de deux franges sombres ou de deux brillantes consécutive) est lié à $λ$ par
la relation $i=λ\frac{D}{a}$
1. Représenter à l'échelle $5$, sur une largeur de $15cm$ :
a) la figure d'interférences obtenue avec la radiation de longueur d'onde $λ_{1}$
b) la figure d‟interférences obtenue avec la radiation de longueur d'onde $λ_{2}$
c) la figure d‟interférences obtenue avec la lumièreémise par la source $F$
2. Qu'observerait –on si la source Fémettait de la lumière blanche  
Exercice 2
A l'aide d'un dispositif interférentiel, on crée deux sources lumineuses $S_{1}$ et $S_{2}$ synchrones et
cohérentes distantes de a. quand le dispositif est éclairé par une source de lumière
monochromatique de longueur d'onde $λ=0,6µm$, on observe des franges d'interférence sur
l'écran $E$ placé à$ D=2,5m$ de $S_{1}$ et $S_{2}$
1. Etablir l'expression de la différence de marche au point $M$ de l'écran
2. Déterminer la distance entre les deux sources pour que la distance entre les milieux de la $6^{e}$
et $9^{e}$ frange brillante située de part et d'autre de la frange centrale numérotée $0$ soit égale à
$1,5cm$
3. Déterminer la nature de la frange en un point $P$ de $E$ distant de $2,5mm$ de la frange centrale
Exercice 3
Deux fentes $F_{1}$ et $F_{2}$ sont éclairées par une fente source en lumière monochromatique rouge de
longueur d'onde $λ=0,64µm$ et se comportent comme deux sources synchrones et en phase. La
figure d'interférence est observée sur un écran. On considère un point $M$ sur un écran situé à
la distanced1 de $F_{1}$ et $d_{2}$ de $F_{2}$ ('schéma)
1. Les vibrations lumineuses issues des fentes $F_{1}$ et $F_{2}$ sont-elles ? Sont –elles en phase
(Justifier les réponses)
2. La vibration lumineuse émise par la fente $F_{1}$ arrive en $M$ avec un certain retard .Exprimer
ce retard en fonction de d1et de la vitesse $c$ de la lumière dans l'air
3. Même question pour la vibration lumineuse issue de la fente $F_{2}$
4. En déduire à quelles conditions le point $M$ sera sur frange brillante ; sur une frange
sombre$5$. Que peut-on dire des points $M$ suivants :
-$M$ est tel que $d_{2}-d_{1}=0$
-$M$ est tel que $d_{2}-d_{1}= 3,20 µm$
-M est tel que $d_{2}-d_{1}=2,24 µm$
Exercice 4                                                                                                                                              
La lumière serait de nature contradictoire. Si une théorie permet d'expliquer de nombreux
phénomènes, elle peut s'avérer insuffisante pour en comprendre d'autres.  
Le but de cet exercice est de montrer que, selon l'expérience réalisée, un des aspects
du comportement de la lumière. $A$ cet effet on réalise le dispositif ci-après :  
1. Dispositif expérimental.  
$(S)$ est une source de lumière qui éclaire                     
deux fentes fines, verticales distantes de $a =
1,5 mm$. La source $(S)$ est équidistante des
deux fentes. $(E)$ est un écran opaque vertical
placé à une distance $D = 2 m$ du plan des
fentes.  
a) Quel phénomène se produit à la sortie
de chaque fente ? Quel aspect de la lumière
permet-il de mettre en évidence ?  
b) Justifier l'utilisation d'une source unique pour éclairer les deux dentes.  
c) Reproduire le schéma et représenter la marche des faisceaux lumineux issus des fentes $F_{1}$
et $F_{2}$. Hachurer le champ où l'on peut observer le phénomène d'interférence.
2. La source $(S)$ émet une lumière monochromatique de longueur d'onde $λ$.
a) Qu'observe-t-on sur l'écran ? Préciser la direction des franges et la nature de la frange
centrale qui se forme en $O$.
b) Pour déterminer la longueur d'onde $λ$, on compte $5$ franges brillantes de part et d'autres de
la frange centrale occupant ensemble une largeur $l = 8 mm$. En déduire la valeur de $λ$.
3. La source précédente $(S)$ est remplacée par une source $(S')$ qui émet simultanément deux
radiations monochromatiques de longueur d'onde $λ_{1} = 0,60 µm$, et $λ_{2} = 0,54 µm$. Il se produit
une superposition des systèmes de franges formées par les deux radiations.
A quelle distance $x$ du point $O$ se produit la première coïncidence de franges brillantes ?
Exercice5
Un pinceau de lumière monochromatique émis par un laser hélium-néon éclaire deux fentes
parallèles séparées par une distance  $a =0,5mm$ . Un écran est placé perpendiculairement au
pinceau lumineuxàunedistance $D=2m$ duplandes fentes. Dessinerle dispositif expérimental.
1. Interpréterlaformationdesfrangesbrillantesetobscures.  
2. Définir et calculer la différence de marche aux $2$ fentes d'un point $M$ de l'écran, pour en
déduirelapositiondesfrangesbrillanteset obscures
3. Préciser la nature de la frange centrale appartenant au plan médiateur des $2$ fentes.             
4. Définir et calculer l'interfrange. Quelle est l'influence des différents paramètres sur
l'interfrange ? Comment doit-on modifier la distance entre les $2$ fentes pour obtenir des
frangesplusespacées ?
5. Calculer la longueur d'onde et la fréquence de la lumière émise par le laser, sachant que $6$
frangessontespacéesde$12,7mm$.
6. Est-ce que la longueur d'onde ou la fréquence change (ou aucune des deux), si le rayon
lumineux se propage dans le verre ? Calculer les nouvelles valeurs. (On sait que dans le verre
lacéléritédelalumièrevaut$200000km/s$.
Exercice6
Une lumière monochromatique, issue d‟une fente $F$, tombe sur un écran $E$ percé de deux
fentes $F_{1}$ et $F_{2}$ parallèleà $F$. Un dispositif spécial permet de faire varier la distance entre les
fentes$F_{1}$ et $F_{2}(F_{1}F_{2}=a$)quirestetoutefoissituéeàégaledistancede$F$.
1. Ondisposeunécran$K$,parallèleàEetàunedistancedde celui-ci.Qu'observe-t-onsurl'écranK
2. La longueurd‟ondedelalumièremonochromatiqueest $λ$.
OnmesuredansleplanKl'intervalleLséparant$N$frangesbrillantesconsécutives.
Etablir la formule donnant a en fonction de $λ, N, d$ et $L$ (On supposera établie la formule de
l'interfrange)   Calculer a lorsque $λ=0,55µm, L=7,2mm, N=7$ et $d=1,20m$  
3. On augmente l'intervalle $a =F_{1}F_{2}$
Qu''en résulte-il sur le phénomène observé sur l'écran ?
D'autre part on remarque que pour un interfrange inférieur à $0,2mm$, l'observation du
phénomène devient très difficile à l'œil nu .Quelle sera la valeur limite $a'$ de la distance $F_{1}F_{2}$
séparant les deux fentes ?
4. Combien observe-t-on de franges brillantes sur l'intervalle $L=7,2mm$ de l'écran $K$ quand
$a=a'$? La mesure de l'intervalle est faite à partir d'une frange brillante   
Exercice7  
1. Soit à la distance de deux fentes fines et parallèles $F$ et $F'$ dans l'expérience de Young. On
éclaire $F$ et $F'$ par une fente lumineuse parallèle aux précédentes et à égale distance de chacune
d'elle. Soit $λ$ la longueur d'onde dans le vide de la lumière monochromatiqueemployée. On
observe dans l'air des franges d'interférences sur un écran $(P)$ parallèle au plan des deux
fentes et situé à une distance $d$ de ces fentes. Soit la largeur de $N$ interfranges consécutifs (on
prendra comme plan de figure un plan perpendiculaire au plan $(F F'))$
1.1. Etablir la relation donnant $λ$ en fonction de $a,d,l$ et $N$.
A N :$a=2,00mm ;l=4,00mm ; N=12$et $d=1,00m$. Calculer $λ$  
1.2. Quelle serait la nouvelle longueur $l$ du même nombre $N $ d'interfranges si tout le dispositif
était plongé dans un milieu d'indice par rapport à l'air
A.N :$n_{o}=1,30$  
1.3. Le système étant placé dans l'air,on recouvre la fente $F$ du côté de l'écran par un verre à
faces parallèles d'épaisseur e et d'indice $n=1,52$ .Qu'observe-t-on sur l'écran.
Expliquer le phénomène. Calculer e si le déplacement de la frange centrale est $X=4,40mm$
1.4. On place sur $F$ une autre lame d'épaisseur $e'$ et d'indice $n'$ ; Le système de franges
obtenu est alors identique à celui réalisé avant la mise en place des deux lames .Donner en
fonction de $e, n$ et $n'$ l'expression de $e'$
Calculer $e'$ si $n'=1,402$.Le dispositif est celui de la question.1, mais la source émet deux
radiations : $λ=0,550 µm$ et $λ = 0,650 µm$.
On observe simultanément les deux franges. Déterminer dans le plan$(P)$, la plus petite
distance par rapport à la frange centrale où les milieux de deux franges brillantes
correspondant aux deux radiations coïncident.
Exercice8
La source $F$ n'est plus monochromatique, mais des filtres permettent d'obtenir des
radiations monochromatiques différentes (voir figure). Pour chaque radiation, on mesure la
longueur d'onde correspondant à $6$ interfranges $i (i$ est la distance séparant le milieu de deux
franges brillantes consécutives ou de deux franges sombres consécutives) (voir figure).
1. Pourquoi mesure-t-on la distance correspondant à $6$ interfranges plutôt que celle mesurant $1$
interfrange ?
2. On a obtenu les résultats suivants. Compléter le tableau.  
Couleur
 

Couleur          
$6i$ $14,1$ $15,6$ $17,4$ $18,3$ $19,5$
$λ (µm)$       $0,47$ $0,52$ $0,58$ $0,61$ $0,65$

3. Tracer la courbe représentative de la fonction $i=f(λ)$ .
4. La relation $i=λ\frac{D}{a}$ est-elle en accord
avec la courbe obtenue précédemment ?  
5. Comment faudrait-il modifier le
dispositif expérimental pour obtenir des mesures
avec une plus grande précision ?  
6. Quelle serait la valeur de l'interfrange obtenu
avec une radiation de longueur d'onde $0,50μm$ ?  
7. Ondisposed‟une source monochromatique de
longueur d'onde inconnue. Comment feriez-
vousexpérimentalementpourladéterminer.
Exercice 9
On réalise une expérience d'interférences lumineuses avec le dispositif d'Young, en utilisant
une lumière monochromatique de longueur d'onde $λ_{1} = 0,52 μm$. La fente-source $F$ éclaire
deux fentes fines identiques $F_{1}$ et $F_{2}$ situées dans un plan vertical et distantes de $F_{1}F_{2} = a =2mm$
.Un écran d'observation $(E)$ est placé à $150 cm$ du plan contenant $F_{1}$ et $F_{2}$
et parallèlement à celui-ci.
1. a- Décrire et expliquer le phénomène observé sur l'écran $(E)$.
b-Quelle conclusion peut-on en tirer quant à la nature de la lumière ?  
2. Définir et calculer l'interfrange $i$.
3. La frange centrale brillante est d'ordre zéro.
Calculer la distance séparant la troisième frange brillante à gauche de la frange centrale
et la deuxième frange noire à droite de cette frange centrale.
La fente-source $F$ émet maintenant une radiation monochromatique de longueur d'onde
$λ_{2} = 0,65μm$.
4. A quelle distance de cette fente-source $F$ doit-on placer l'écran d'observation $(E)$ pour que
l'nterfrange $i'$ obtenu avec ce dispositif soit égal à l'interfrange $i$ de la question $2$ ? La
distance entre la fente-source $F$ et le plan contenant $F_{1}$ et $F_{2}$ est égale à $50 cm$.  
5. La fente-source $F$ émet simultanément les deux radiations de longueurs d'onde
$λ_{1}= 0,52 μm$ et $λ_{2}= 0,65 μm$.
On remet l'écran $(E)$ à la position où il est distant de $150 cm$ du plan contenant $λ_{2}= 0,65 μm$.
On remet l'écran $(E)$ à la position où il est distant de $150 cm$ du plan contenant $F_{1}$ et $F_{2}$.  
6. A quelle distance de la frange centrale aura lieu la première coïncidence des franges
brillantes des deux systèmes de franges obtenus.
Exercice10                                                                                              
Le dispositif des fontes d'YOUNG schématisé sur la figure -1 permet de réaliser une
expérience de mise en évidence d'interférences lumineuses. La source $(S)$ émet une
lumière monochromatique delongueur d'onde $λ=0,6.10^{-6} m(P)$ est un
plan opaque comportant deux fentes fines
$S_{1}$ et $S_{2}$ distantes de $a = 1mm$ et     
assimilables à deux sources ponctuelles
monochromatique symétriques par
rapport à un point $I$ milieu de $S_{1}S_{2}$.Un
écran $(E)$ est disposé parallèlement à $(P)$
 et à une distance $D = 2 m$ de celui-ci.
On observe des interférences lumineuses
dans la représenté hachurée sur le schéma
où les deux faisceaux issus de $S_{1}$ et $S_{2}$
couvrent une partie commune. L'intersection de cette zone hachurée avec l'écran $(E)$ est un
ensemble de franges brillantes équidistantes ayant la couleur de lumière monochromatique.
Deux franges brillantessuccessives sont séparées par une frange sombre, et la frange centrale
en $O$ est brillante. Un point$ M$ du champ d'interférence est repéré par son abscisse $x=
OM$ Lorsque $M$ appartient à une frange brillante, ilvérifielarelation$MS_{2}-MS_{1}=kλ$ (aveckentier).
Par contre s'il appartient à une frange sombre il vérifie la relation $MS_{2}- MS_{1}= (2k+1)\frac{λ}{2}$
   (aveckentier).  
1) a -Montrer que la différence de marche a pour expression $(MS_{2}- MS_{1}) =\frac{ax}{D}$   
b -En déduire l'expression de l'abscisse $x$ d'un point $M$ de l'écran en fonction de $λ, D$ et $ a $:  
- Lorsqu'ilappartientàunefrange brillante
-Lorsqu'ilappartientàunefrangesombre.  
2) a -Déterminer l'expression de l'interfrange $i$ en fonction de $λ, D$ et
a. Calculer $i$.  
b -Préciser, en le justifiant, la nature (brillante ou sombre) de la frange d'abscisse $x = - 4,2 mm$.
3) Onapporteleschangementssuivantsaudispositif expérimental de la figure $-1$ :  
-on supprime la source $(S)$ et le plan opaque $(P)$- à l'emplacement des deux sources
secondaires $S_{1}$ et $S_{2}$ on dispose de deux sources $S'_{1}$et $S'_{2}$ totalement indépendantes, émettant
chacune la lumière monochromatique de longueur
d'onde $l = 0,6.10^{-6}m$. (figure -2) on n'observe
d'interférences lumineuses. Expliquer pourquoi ?
4) Citer un dispositif, autre que les fentes
d'YOUNG, permettant de réaliser
une expérience de mise en évidence
d'interférences lumineuses :  
- on tracera la marche des rayons lumineux                                                                               
- et on hachurera la zone où les deux
faisceaux lumineux, issus des deux sources
secondaires, couvrent une partie commune
correspondant aux interférences lumineuse.

Série d'exercices : Induction magnétique - Étude d'un dipôle RL - Ts

Classe: 
Terminale
 

Exercice 1

I. Une bobine d'inductance $L$ et de résistance négligeable est reliée à un microampèremètre, comme l'indique la figure ci-dessous.
 
 
On rapproche l'aimant vers la bobine,
 
1) Quel est le phénomène observé
 
2) Indiquer le sens de circulation du courant induit dans la bobine
 
3) Préciser l'inducteur et l'induit
 
II. Avec la bobine précédente, on branche en série un résistor de résistance $R=10\,K\Omega$ et un générateur basse fréquence $(G.B.F$ à masse flottante$)$ qui délivre une tension triangulaire alternative. 
 
Sur l'écran d'un oscilloscope bicourbe, on visualise la tension $u_{AB}$ sur la voie $Y_{A}$ et la tension $u_{CB}$ sur la voie $Y_{B}$ (figure 4 page 3).
 
1) On note $i(t)$ l'intensité instantanée du courant qui traverse le circuit, son sens positif choisi est indiqué sur le schéma du montage.
 
a) Montrer, sans calcul, que la bobine est le siège d'un phénomène d'auto-induction
 
b) Montrer que la tension aux bornes de la bobine est $$u_{AB}=\dfrac{-L}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}$$
 
 
c) Justifier littéralement l'allure de la tension sur la voie $Y_{A}$
 
2) Les réglages de l'oscilloscope sont :
 
Sensibilité verticale de la voie $Y_{A}$ : $0.2V\cdot div^{-1}$
 
Sensibilité verticale de la voie $Y_{B}$ : $2V\cdot div^{-1}$
 
Sensibilité horizontale : $0.2\,ms\cdot div^{-1}$
 
A partir des oscillogrammes :
 
a) Calculer la période $T$ et la fréquence $N$ des tensions
 
b) Pendant la première demi-période, déterminer les expressions de $u_{AB}$ et de $u_{CB}$ en fonction du temps.
 
c) En déduire la valeur de l'inductance $L$ de la bobine. 
 
Puis indiquer sa significationphysique.
 
 
 
 

Exercice 2

Dans une bobine $B_{1}$ qui est fermée sur un résistor de résistance $R$ on introduit une bobine $B_{2}$ qui est alimentée par un générateur de courant réglable.( voir figure)
 
 
1 On introduit $B_{1}$ dans $B_{2}$ en gardant les deux axes de révolution des deux bobines confondus.
 
a) Représenter le champ magnétique créé par la bobine $B_{2}$
 
b) Énoncer la loi de Lenz. 
 
Représenter le champ magnétique induit dans la bobine $B_{1}.$ 
 
En déduire le sens du courant induit.
 
c) Préciser l'inducteur et l'induit.
 
2) La bobine $B_{2}$ est fixée à l'intérieur de $B_{1}$, on diminue l'intensité du courant débitée par le générateur
 
a) Comment varie la valeur du champ magnétique créé par la bobine $B_{2}.$
 
b) Représenter le champ magnétique créé par $B_{2}$ et celui qui est induit dans $B_{1}.$
 
c) Préciser le sens du courant induit dans $B_{1}.$
 
3) On modifie les bornes du générateur et on répète l'expérience de la question 1, représenter le champ magnétique induit dans la bobine $B_{1}.$

Exercice 3

On réalise le montage série comportant une bobine d'inductance $L$ et de résistance négligeable, une résistance de valeur $R=10k\Omega$ ainsi qu'un générateur basse fréquence dont la masse n'est pas reliée à la terre(masse flottante).
 
1) Réaliser le schéma de principe du montage. 
 
Ajouter les branchements à effectuer pour visualiser la tension aux bornes de la bobine sur la voie $A$ et la tension aux bornes de la résistance $R$ sur la voie $B.$
 
base de temps : $0.5\,ms/div$
sensibilité voie $A$ : $0.1V/div$
sensibilité voie $B$ : $2V/div$
 
2) L'une de ces tensions permet d'observer l'allure de $i(t).$ 
 
Laquelle ? 
 
justifier la réponse.
 
3) L'oscillogramme ci-après donne l'allure des différentes tensions observées. 
 
Déterminer la période $T$ de l'intensité du courant.
 
4) Déterminer l'amplitude $I_{m}$ (valeur maximale atteinte) de l'intensité du courant.
 
5) On considère, sur l'oscillogramme précédent, une demi-période où la tension $u_{L}$ aux bornes de la bobine est positive.
 
a) Déterminer la valeur de la tension $u_{L}.$
 
b) Déterminer la valeur de la dérivée par rapport au temps de l'intensité du courant.
 
c) En déduire la valeur $L$ de l'inductance de la bobine.

Exercice 4

Deux rails conducteurs $(AA')$ et $(CC')$, parallèles et de résistances négligeables, séparés par une distance $L=25\,cm.$ 
 
Une tige $(MN)$ métallique de masse négligeable, perpendiculaire aux rails, peut glisser sans frottement dans une direction parallèle aux rails. (Voir figure)
 
 
La résistance de la longueur $L$ de la tige est $r=0.5\Omega.$
 
L'ensemble est placé dans un champ magnétique uniforme $\overrightarrow{B}$ d'intensité $B=1T.$
 
1) On branche entre les extrémités $A$ et $C$ des deux rails un générateur $G$ de courant continu, on remarque que la tige se met en mouvement en se dirigeant de $A$ vers $A'.$ 
 
Déterminer la direction et le sens du vecteur champ magnétique $\overrightarrow{B}.$
 
2) On élimine le générateur $G$ et on le remplace par un fil conducteur puis on déplace la tige $MN$ de sa position initiale $AC$ vers la droite sur les rails, à une vitesse $V=10\,m\cdot s^{-1}.$
 
a) Choisir sur le circuit un sens positif et tracer le vecteur surface $S.$
 
b) Déterminer l'expression du flux magnétique à travers le circuit pour une position quelconque de la tige $(MN)$ en fonction du temps. 
 
Montrer que ce flux s'écrit sous la forme :
 
$\Phi=B\cdot L\cdot V\cdot t.$
 
2) a) Calculer la force électromotrice induite
 
b) Calculer l'intensité $i$ du courant induit
 
c) Déterminer le sens du courant induit.
 
b) Représenter $i$ sur le schéma

Exercice 5

Une spire plane de surface $s=2.5\,cm^{2}$ de résistance $r'=2\Omega$, placée à l'intérieur d'un solénoïde de longueur $l=40\,cm$, de rayon $R=5\,cm$, comportant $103$ spires et de résistance $r=2\Omega$ perpendiculairement à son axe $(\Delta).$ 
 
Le solénoïde est parcouru par un courant d'intensité $i(t)$ qui varie selon la courbe suivante :
 
 
1) a) Établir l'expression de l'inductance $L$ du solénoïde. 
 
Calculer sa valeur
 
b) Donner l'expression de $i(t)$ dans chaque intervalle de temps.
 
c) Quel est le phénomène qui se produit dans le solénoïde ? 
 
Justifier la réponse.
 
d) Calculer la $f.e.m$ induite dans le solénoïde dans chacun des intervalles de temps $[0\;;\ 2\,ms]$ et $[2\;;\ 6\,ms].$
 
e) Représenter cette $f.e.m$ au cours du temps.
 
2) Représenter, en respectant le sens positif choisi, dans chacun des intervalles $[0\;;\ 2\,ms]$ et $[2\;;\ 6\,ms]$ respectivement sur la spire et sur le solénoïde le sens du courant induit et le sens du courant principal.
 
3) Calculer aux instants $t_{1}=2\,ms$ ; 
 
$t_{2}=4\,ms$ et $t_{3}=6\,ms$ :
 
a) La tension aux bornes du solénoïde.
 
b) L'énergie magnétique emmagasinée par le solénoïde.

Exercice 6

On réalise le montage de la figure 1 où $R=10\Omega$, $E=9V$, $L$ et $r$ sont inconnues.
 
 
I. à l'origine du temps, on ferme l'interrupteur $K.$ 
 
Un oscilloscope à mémoire permet d'obtenir les chronogrammes de la figure 2.
 
 
1) Reproduire le schéma du circuit en indiquant les branchements nécessaires qui permettent d'obtenir le chronogramme $1$ sur la voie $Y_{1}$ et le chronogramme $2$ sur la voie $Y_{2}.$
 
2) Interpréter la réponse du dipôle $RL$ à l'échelon de tension.
 
II.
 
1) Montrer que l'équation différentielle régissant les variations de la tension aux bornes du résistor $u_{R}(t)$ s'écrit sous la forme $$L\dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+(R+r)u_{R}=RE.$$
 
2) Sachant que la solution de cette équation différentielle est de la forme $u_{R}(t)=A(1-\mathrm{e^{-\alpha\,t}}).$
 
Montrer que $A=\dfrac{RE}{R+r}$ et $\alpha=\dfrac{R+r}{L}$ 
 
3) a) En régime permanent, déterminer graphiquement
 
$-\ $ l'intensité du courant $I_{p}.$
 
$-\ $ la tension $u_{B}$ aux bornes de la bobine.
 
b) en déduire que la résistance de la bobine est $r=8\Omega.$
 
c) Déterminer graphiquement la valeur de la constante de temps $\tau.$
 
Déduire la valeur de l'inductance $L$ de la bobine.

Exercice 7

On alimente un dipôle $"$bobine - résistance $R"$ par un générateur basse fréquence en série avec un dipôle ohmique de protection. 
 
Aucune des bornes de sortie du générateur n'est reliée à la Terre. 
 
La mesure de la résistance de la bobine donne $r=15\Omega$ et $R$ est une résistance variable.
 
 
L'oscilloscope est branché comme indiqué sur le schéma (fig 1). 
 
La touche $ADD$ de l'oscilloscope permet d'observer la somme $u_{S}$ des tensions des deux voies $1$ et $2$, $u_{S}=u_{1}+u_{2}.$ 
 
Sur la figure 2, on a reproduit avec la même origine des temps les courbes $u_{1}(t)$ et $u_{S}(t).$
 
1) Exprimer en fonction de $i$, $r$, $R$ et $L$ les tensions suivantes : $u_{1}$, $u_{2}$, $u_{S}(t).$
 
2) L'oscillogramme ci-dessus a été obtenu en ajustant $R$ à la valeur de $r.$
 
Montrer que dans ce cas $u_{S}=-\dfrac{L\mathrm{d}u_{1}}{r\mathrm{d}t}.$
 
3) En exploitant les chronogrammes de la figure 2, déterminer $L.$

Exercice 8

Un dipôle est constitué de l'association en série d'une bobine présentant une inductance $L$ et une résistance $R_{L}$ avec un conducteur ohmique de résistance $R=40W.$ 
 
Ce dipôle est alimenté par un générateur de tension de $f.é.m.$ 
 
 
$E$ à travers un interrupteur $K.$ 
 
Il est parcouru par un courant $i.$
 
Les bornes $A$, $B$, et $C$ sont reliées aux entrées d'une carte d'acquisition permettant d'enregistrer l'évolution des tensions. 
 
A l'instant $t=0$, on ferme l'interrupteur $K$, l'enregistrement génère les courbes $1$ et $2.$
 
 
1) Quelle tension est représentée par la courbe 1 ?
 
2) Quelle tension est représentée par la courbe 2 ?
 
 
3) Quelle sera l'allure de la courbe de variation du courant $i$ choisie parmi les quatre courbes ci-dessous ?
 
4) Tracer l'allure de la courbe de variation de la tension $u_{AB}.$
 
5) Donner la valeur $E$ et l'intensité maximale $I_{max}$ atteinte par $i.$
 
6) Donner l'équation différentielle définissant $i.$ 
 
Cette équation sera présentée sous la forme d'une égalité où la $f.é.m.$ 
 
$E$ sera le seul terme du deuxième membre. 
 
En déduire les valeurs de $L$ et $R_{L}.$ 
 
On remplace maintenant le générateur de tension par un générateur de courant délivrant un courant en dents de scie (courbe 3). 
 
 
On considérera ici que la résistance $R_{L}$ de la bobine est nulle.
 
7) Quelle sera, parmi les cinq courbes ci-dessous, l'allure de la courbe de variation de la tension $u_{AB}$ et de la courbe de variation de la tension $u_{BC}.$
 
 

Exercice 9

On réalise un circuit électrique $AM$ comportant en série un conducteur ohmique de résistance $R=50\Omega$, une bobine $(B_{1})$ d'inductance $L$ et de résistance supposée nulle et un interrupteur $K.$ 
 
Le circuit $AM$ est alimenté par un générateur de tension de force électromotrice $(f.e.m)$ E (fig 1). 
 
 
Un système d'acquisition adéquat permet de suivre l'évolution au cours du temps des tensions $u_{AM}$ et $u_{DM}.$
 
A l'instant $t=0s$, on ferme l'interrupteur $K.$ 
 
Les courbes traduisant les variations de $u_{AM}(t)$ et $u_{DM}(t)$ sont celles de la figure 2
 
 
1) a) Montrer que la courbe 1 correspond à $u_{DM}(t).$
 
b) Donner la valeur de la $f.e.m$ du générateur.
 
2) a) A l'instant $t_{1}=10\,ms$, déterminer graphiquement la valeur de la tension $u_{B1}$ aux bornes de la bobine $(B_{1})$ et déduire la valeur de la tension $u_{R}$ aux bornes du conducteur ohmique.
 
b) A l'instant $t_{2}=100\,ms$, montrer que l'intensité du courant électrique qui s'établit dans le circuit électrique est $I_{0}=0.12\,A$
 
3) a) Déterminer graphiquement la valeur de la constante de temps $\tau$ du dipôle $RL.$
 
b) Sachant que $\tau=L/R$, déterminer la valeur de l'inductance $L$ de la bobine $(B_{1})$
 
c) Calculer l'énergie emmagasinée dans la bobine en régime permanent
 
4) On remplace la bobine $(B_{1})$ par une bobine $(B_{2})$ de même inductance $L$ mais de résistance $r$ non nulle. 
 
Les courbes traduisant les variations de $u_{AM}(t)$ et $u_{DM}(t)$ sont celles de la figure 3.
 
 
a) Montrer qu'en régime permanent, la tension aux bornes de la bobine $(B_{2})$ est donnée par la relation $u_{B_{2}}=\dfrac{r\,E}{R+r}$
 
b) Déduire la valeur de la résistance $r$

Exercice 10

On se propose d'étudier l'établissement du courant dans un dipôle série comportant une bobine d'inductance $L$ et une résistance $r$ et un conducteur ohmique de résistance $R_{0}=30\Omega$ lorsque celui-ci est soumis à un échelon de tension de valeur $E$ délivrée par un générateur de tension idéal. 
 
Un oscilloscope à mémoire, est branché comme l'indique la figure 1, permet d'enregistrer au cours du temps les valeurs des tensions.
 
 
1) A l'instant $t=0$, on ferme l'interrupteur $K$, et on procède à l'enregistrement. 
 
On obtient les courbes $y_{1}=f(t)$ et $y_{2}=g(t)$ (figure 2).
 
 
a) Quelles sont les grandeurs électriques observées sur les voies $A$ et $B$ ? 
 
Identifier $y_{1}$ et $y_{2}.$ 
 
Justifier la réponse.
 
b) Quelle est la courbe qui permet de déduire la variation de l'intensité de courant $i$ au cours du temps ? 
 
Expliquer brièvement le comportement électrique de la bobine.
 
c) Prélever du graphe la valeur de la force électromotrice du générateur.
 
2) Lorsque le régime permanent est établi, l'intensité $i$ prend la valeur $I_{p}$, tandis que $y_{2}$ prend la valeur $Y_{p}$
 
a) Donner, dans ces conditions, les expressions littérales des tensions $u_{AM}$, $u_{AB}$ et $u_{BM}.$
 
Montrer, en utilisant les courbes de la figure 2, que la bobine a une résistance $r$ non nulle.
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Loi de Laplace - Ts

Classe: 
Terminale
 

Exercice 1

Une tige en cuivre $OM$ parcourue par un courant de haut en bas d'intensité $I_{1}=7A$ peut articuler librement en $« O »$ et son extrémité $M$ touche une solution conductrice. 
 
On approche d'elle une deuxième tige $AN$ en cuivre de longueur $L=12\,cm$ qui peut articuler librement en $A$ et son extrémité $N$ touche une solution conductrice voir (figure 1).
 
 
Lorsque la tige $AN$ est parcourue par un courant $OA$
 
De haut en bas d'intensité $I_{2}=5A$ sa partie inférieure de longueur $l=4\,cm$ plonge dans le champ magnétique $\overrightarrow{B_{1}}$ $MN$ uniforme, perpendiculaire au plan de la feuille, de sens sortant et de valeur $0.3T.$
 
1) donner le sens d'inclinaison de la tige $AN.$
 
2) a) donner les caractéristiques de la force de la place $\overrightarrow{F}$ qui agit sur la tige $AN$
 
b) représenter $\overrightarrow{F}$
 
c) déterminer la masse de la tige $AN$, sachant qu'elle s'écarte de la verticale d'un angle $\theta=10^{\circ}.$
 
On donne $g=10\,N\cdot Kg^{-1}.$
 
3) La partie supérieure de la tige $OM$ de longueur $l'=3\,cm$ plonge dans le champ magnétique $\overrightarrow{B_{2}}$ uniforme, normale au plan de la feuille et de sens rentrant crée par la tige $AN.$
 
a) est-ce que il y a une interaction entre les deux tiges ? 
 
Expliquer
 
b) quel est la nature de l'interaction ? 
 
Si elle existe ?
 
c) donner le sens d'inclinaison de la tige $OM$
 
d) Donner l'expression de l'intensité du champ magnétique $\overrightarrow{B_{2}}.$

Exercice 2

Un fil conducteur en cuivre $OA$ rigide et homogène, de masse $m$, de longueur $l$, est suspendu par son extrémité supérieure en $O$ à un axe fixe $\Delta$, autour duquel il peut tourner sans frottement ; sa partie inférieure plonge dans une cuve contenant du mercure lui permettant de faire partie d'un circuit électrique comprenant un rhéostat et un générateur de tension continue $G$ qui plonge dans une région où règne un champ magnétique uniforme $B$ orthogonal au plan de la figure.
 
En fermant l'interrupteur $K$, un courant électrique d'intensité $I$ traverse le fil $OA$ et celui-ci prend la position indiquée par le schéma ci-dessous.
 
 
1) Représenter les forces exercées sur le fil.
 
2) Indiquer sur le schéma le sens du courant électrique.
 
3) En appliquant la condition d'équilibre à la tige,
 
Calculer l'angle $\alpha$ que fait le fil conducteur avec la verticale.
 
On donne $I=5A$, 
 
$l=25\,cm$, 
 
$m=8\,g$ et $\|B\|=0.05T.$

Exercice 3

On considère le dispositif suivant appelé : Balance de Cotton.
 
Les extrémités du fil conducteur sont reliées à un générateur de tension continue débitant un courant d'intensité $I.$ 
 
On ajoute sur le plateau une masse marquée $m$ pour équilibrer la balance. 
 
Ainsi on remplit le tableau de valeurs suivant :
$$\begin{array}{|c|c|c|c|c|c|c|} \hline I(A)&0&2&4&6&8&10\\ \hline m(g)&0&0.4&0.8&1.2&1.6&2\\ \hline \end{array}$$
 
1) Tracer la courbe $m=f(I).$
 
2) En appliquant la condition d'équilibre à la balance, établir la relation théorique $m=f(I).$
 
3) Déduire la valeur du champ magnétique $\|B\|.$ 
 
On donne $L=2\,cm$ et $d'=5/4\cdot d$
 
4) Peut-on accrocher une masse $m=2.45\,g$, sachant que le fil conducteur de la balance ne peut supporter qu'une intensité de $12\,A$, pour que la balance soit en équilibre.
 
 

Exercice 4

On néglige les forces de frottement et le champ magnétique terrestre.
 
Deux barres conductrices sont disposées parallèlement suivant la ligne de plus grande pente d'un plan incliné d'un angle $\theta$ sur l'horizontale. 
 
Elles sont distantes de $L$ ; leurs extrémités supérieures sont reliées entre elles par un générateur $G$ et par un interrupteur $K.$ 
 
Une barre $MN$ conductrice est posée perpendiculairement sur les deux barres précédentes. 
 
Le contact électrique se fait en $M$ et $N.$ 
 
On crée dans la région où se trouve la barre $MN$ un champ magnétique uniforme $\overrightarrow{B}$ perpendiculaire au plan des rails. 
 
On ferme $K.$ 
 
Un courant d'intensité $I$ circule dans le montage.
 
1) Représenter les forces exercées sur la barre $MN$ pour qu'elle puisse être en équilibre (on peut utiliser la vue de droite). 
 
Déduire le sens de $\overrightarrow{B}$
 
2) La barre $MN$ a une masse $m=10\,g$ et pour qu'elle soit en équilibre il faut que l'intensité du courant soit égale à $I_{1}=10\,A.$
 
 
a) Établir la condition d'équilibre de la barre $MN$
 
b) Exprimer la norme de $\overrightarrow{B}$ en fonction de $I_{1}$, $L$, $m$, $g$ et $\theta$ pour que la barre reste en équilibre. 
 
Montrer que $\|\overrightarrow{B}\|=68\,mT.$
 
On donne : 
 
$\theta=20^{\circ}$ ; 
 
$g=10\,N/kg$ et $L=0.05\,m.$
 
L'intensité du courant est $I_{2}=15\,A$ et on garde le champ magnétique $\overrightarrow{B}$ précédent, on place sous la barre $MN$ un ressort à spires non jointives, de raideur $k$ de masse négligeable dont la direction est celle de la plus grande pente du plan incliné (voir figure ci-dessous).    
 
 
Lorsque l'interrupteur $K$ est ouvert la barre $MN$ est en équilibre. 
 
On ferme l'interrupteur $K$, la barre $MN$ prend une nouvelle position d'équilibre $M'N'$ tel que le ressort soit allongé de $\Delta\;l=3.36\,mm.$
 
a) Représenter les forces exercées sur la barre $MN$ (on peut utiliser la vue de droite).
 
 
b) Établir la condition d'équilibre de la barre. 
 
Déduire la valeur de la constante de raideur $k$ du ressort.

Exercice 5

On donne $\|\overrightarrow{g}\|=10\,N\cdot Kg^{-1}$
 
On considère le dispositif représenté sur la figure 1 :
 
 
$OA$ est une tige conductrice de longueur $OA=L=40\,cm$ de masse $m=3\,g$, mobile autour d'une axe horizontal passant par son extrémité $O.$
 
L'autre extrémité $A$ est reliée à un fil souple conducteur ne gênant nullement le mouvement possible de la tige.
 
Cette tige est soumise à l'action d'un champ magnétique uniforme $\overrightarrow{B_{1}}$ perpendiculaire au plan de la figure de valeur $\|\overrightarrow{B_{1}}\|=0.1\,T.$ 
 
Ce champ $\|\overrightarrow{B_{1}}\|$ règne dans une région limitée par $AC=l=10\,cm.$
 
Au point $M$ de la tige tel que $OM=10\,cm$ est attaché un ressort horizontal ; isolant de raideur $K=23\,N\cdot m^{-1}.$
 
Lorsque la tige est traversée par un courant d'intensité $I_{1}=10\,A$ ; elle dévie d'un angle $\alpha=8^{\circ}$ et se stabilise dans une nouvelle position d'équilibre (voir figure 2).
 
On suppose que la déviation $\alpha$ est faible de façon que la partie plongée dans le champ reste sensiblement la même et le ressort reste horizontal et allongé de $\Delta\;l.$
 
1) a) Indiquer le sens du courant traversant la tige.
 
b) Donner les caractéristiques de la force de la place exercée sur la tige.
 
2) a) Faire le bilan des forces exercées sur la tige lorsqu'elle parcourue par le courant $I_{1}.$
 
b) En appliquant le théorème des moments à la tige, déterminer l'allongement du ressort $\Delta\;l.$
 
3) On enlève le ressort et on superpose au champ $\overrightarrow{B_{1}}$ un autre champ $\overrightarrow{B_{2}}$ perpendiculaire au plan de la figure et opposé à $\overrightarrow{B_{1}}.$
 
Le champ $\overrightarrow{B_{2}}$ règne dans une région de façon que la tige soit totalement plongée dans cette région.
 
La tige est toujours parcourue par le même courant $I_{1}=10\,A$ et dans le même sens que 2) ;
 
La déviation de la tige par rapport à la verticale est alors $\theta=4^{\circ}$ ;
 
a) Faire le bilan des forces exercées sur la tige.
 
b) Déterminer la valeur du champ magnétique $\overrightarrow{B_{2}}.$
 
4) Dans cette question la tige $OA$ est isolée du montage précèdent ; elle est liée au bras d'une balance dont les deux bras sont isolants et égaux.
 
La tige est maintenue horizontale dans un plan perpendiculaire au plan de la figure 3 et elle est parcourue par un courant d'intensité $I_{3}$
 
 
Ce courant est amené par deux fils souples et de masse négligeable.
 
La tige est complètement plongée dans un champ $\overrightarrow{B_{3}}$ horizontal et contenu dans le plan de la figure tel que $\overrightarrow{B_{3}}=5\cdot 10^{-2}T.$
 
En l'absence de courant $I_{3}$ ; la tige $OA$ et le fléau sont en équilibre horizontaux.
 
Lorsque la tige est traversée par $I_{3}$ ; il faut placer une masse $m_{0}=4\,g$ sur le plateau $P$ pour rétablir l'équilibre horizontal.
 
a) Déduire de ces expériences les caractéristiques de la force de Laplace.
 
b) Préciser le sens du courant $I_{3}$ et calculer sa valeur.

Exercice 6

On considère le dispositif de la figure 1 qui est constitué de :
 
 
$-\ $ deux rails en cuivre $AD$ et $CE$ horizontaux.
 
$-\ $ Une tige $(T)$ en cuivre, pouvant glisser sans frottement sur les rails. 
 
Sa partie centrale de longueur $l=10\,cm$ baigne dans un champ magnétique $\overrightarrow{B}$ vertical.
 
Un fil $(f)$ inextensible, de masse négligeable, attaché par l'une de ses extrémités au milieu de la tige $(T)$ et par l'autre extrémité à un ressort de masse négligeable et de raideur $k=10\,N\cdot m^{-1}.$ 
 
L'autre extrémité du ressort étant fixe.
 
Une poulie $(P)$ de masse négligeable pouvant tourner sans frottement autour de son axe.
 
$-\ $ Un rhéostat $Rh$ permettant la variation de l'intensité $I$ de courant dans le circuit.
 
1) a) Représenter sur un schéma clair les forces qui s'exercent sur la tige $(T).$
 
On rappelle que la tension du ressort est de la forme $T=k\cdot x$
 
b) A quelle force est du l'allongement du ressort ? 
 
Préciser le sens et la direction de cette force.
 
c) Indiquer, en le justifiant le pôle nord et le pôle sud de l'aimant.
 
2) A l'aide du rhéostat on fait varier l'intensité $I$ du courant dans le circuit et on note l'allongement $x$ du ressort lorsque la tige $(T)$ est en équilibre. 
 
Les résultats des mesures ont permis de tracer la courbe : $I=f(x)$ de la figure 2
 
 
a) Montrer que l'équation de la courbe est de la forme : $I=a\,x.$
 
b) Donner la signification mathématique et la valeur de $a.$
 
c Écrire la relation qui lie $B$, $I$, $k$, $x$ et $L.$
 
d) En déduire l'intensité $B$ du champ magnétique qui règne entre les branches de l'aimant en $U.$
 
3) On détache la barre, on inverse le sens du courant dans le circuit, dont l'intensité est fixée à $I=1A.$ 
 
Pour maintenir la tige $(T)$ en équilibre sur les rails, on incline le plan horizontal supportant le dispositif de $\alpha=15^{\circ}.$ (Figure 3)
 
 
a) Représenter les forces qui s'exercent sur la tige.
 
b) Montrer que la masse $m$ de la tige $(T)$ est donnée par l'expression :
 $m=\dfrac{IBL}{g\sin\alpha}$,
  
c) Calculer sa valeur.
 
On donne : $g=9.8\,N\cdot Kg^{-1}$
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Mouvement d'une particule chargée dans un champ magnétique uniforme - Ts

Classe: 
Terminale
 

Exercice 1

1) On considère les ions de deux isotopes de mercure $_{80}^{200}Hg^{2+}$ et $_{80}^{202}Hg^{2+}$ de masses respectives $m_{1}=3.32\cdot10^{-25}kg$ et $m_{2}=3.35\cdot10^{-25}kg$ et de même charge $q=2e.$ 
 
Ils sont ensuite émis sans vitesse par la source $S$, puis accélérés par un champ électrostatique uniforme qui règne entre $S$ et $P$ tel que $U_{SP}=U=600V.$ 
 
 
 
a) Déterminer l'expression littérale de la vitesse $\|\overrightarrow{V}\|$ en $A$ d'un ion de masse $m$ et de charge $q$ en fonction de $m$, $e$ et $U.$
 
b) Montrer que les deux ions $_{80}^{200}Hg^{2+}$ et $_{80}^{202}Hg^{2+}$ émis par $S$ arrivent en $A$ avec des vitesses différentes.
 
2) Ces deux ions pénètrent en $A$ dans une région où règne un champ magnétique uniforme $\overrightarrow{B}$ perpendiculaire au plan de la figure et tel que $\|\overrightarrow{B}\|=0.2T$ qui leur impose une trajectoire circulaire de rayon $R$, puis ils impressionnent une plaque photographique en deux points $I$ et $F.$
 
a) Établir l'expression de $R$ en fonction de $m$, $e$, $\|\overrightarrow{B}\|$ et $\|\overrightarrow{V}\|$ puis en fonction de $m$, $e$, $\|\overrightarrow{B}\|$ et $U.$
 
b) Calculer $R_{1}$ et $R_{2}$ et déduire la distance $IF$ entre les deux points d'impact, sur la plaque photo des ions des deux isotopes de mercure $Hg^{2+}$

Exercice 2

Un cyclotron est un instrument qui sert à accélérer des particules chargées, permettant ensuite de réaliser des expériences de physique nucléaire. 
 
Dans ce problème les particules chargées sont des protons de masse $m_{p}=1.67\cdot10^{-27}kg$ et de charge électrique $q_{p}=+1.6\cdot10^{-19}C$
 
Le cyclotron est formé de deux demi-cylindres conducteurs creux appelés « dees » et séparés par un intervalle étroit. 
 
Un champ magnétique uniforme $B$ règne à l'intérieur de chaque « dee », sa direction est parallèle à l'axe de ces demi-cylindres, sa valeur est $1.0T.$
 
Un champ électrique $E$ variable dans le temps, peut être établi dans l'intervalle étroit qui sépare les « dees ». 
 
Il permet d'augmenter la vitesse des protons chaque fois qu'ils pénètrent dans cet intervalle.
 
Ce champ électrique variable est obtenu en appliquant une tension sinusoïdale de valeur maximale $U_{M}$ et de fréquence $f$ entre les deux « dees »: $U_{M}=2\cdot10^{3}V$
 
 
1. Le proton entre dans le « dee » $1$ avec une vitesse initiale d'injection $V_{0}$ perpendiculaire à l'axe des demi-cylindres. 
 
On négligera le poids du proton devant la force magnétique.
 
1.1 Donner l'expression de la force agissant sur le proton en $O$ ; la représenter sur un schéma
 
1.2 Le mouvement du proton étant plan, montrer que la valeur de la vitesse est constante.
 
1.3 Montrer que la trajectoire est circulaire de rayon $R_{0}=\dfrac{m_{p}}{q_{pB}}V_{0}$
 
2.1 Exprimer la longueur parcourue par un proton sur le demi-tour de rayon $R_{0}.$
 
2.2 En déduire l'expression du temps $t$ mis par ce proton pour effectuer ce demi-tour.
 
2.3 Ce temps dépend-il de la vitesse d'entrée du proton dans le « dee » ? 
 
Calculer la valeur de $t.$
 
3. Le proton, après avoir fait un demi-cercle dans un « dee », entre dans l'intervalle étroit où il est accéléré par le champ électrique considéré comme constant, maximum et colinéaire au vecteur vitesse du proton durant son passage.
 
Calculer la fréquence $f$ de la tension alternative appliquée entre les « dees » pour que les protons subissent une accélération maximale à chaque traversée de l'intervalle. 
 
On suppose que le temps de traversée de l'intervalle est négligeable devant le temps passé dans les « dees ».
 
4.1 Exprimer littéralement, puis calculer la variation d'énergie cinétique $\Delta\,Ec$ du proton lorsqu'il traverse l'intervalle étroit. 
 
Le résultat sera exprimé en joule puis en électron-volt.
 
4.2 Préciser si le rayon de la trajectoire du proton augmente ou diminue à chaque fois qu'il traverse l'intervalle étroit (justifier la réponse)
 
5. La vitesse d'injection du proton étant supposée pratiquement nulle, on désire que sa vitesse atteigne $2\cdot10^{4}km\cdot s^{-1}$
 
Calculer le nombre de tours que le proton devra décrire dans le cyclotron.
 
6. Calculer la valeur du rayon à partir duquel les protons ayant acquis une vitesse de $2\cdot10^{4}km\cdot s^{-1}$ seront extraits, en admettant qu'ils sont injectés à proximité immédiate du centre $O$ du cyclotron

Exercice 3 : Utilisation d'un spectrographe de masse 

Sur le schéma ci-dessous, on retrouve la même zone $I$ d'ionisation fournissant les ions $X^{+}.$ 
 
On a ensuite la zone $II$ où on applique une tension accélératrice : $U'=8.00\,kV$ entre les plaques $P_{1}$ et $P_{2}$ permettant de donner aux ions $X^{+}$ une vitesse $v'.$ 
 
Dans la zone $III$ un dispositif de filtrage permet d'éliminer les éventuelles particules parasites qui auraient pu être obtenues par fragmentation des molécules $X$ lors de l'ionisation par choc électronique. 
 
Enfin dans la zone $IV$ existe un champ magnétique de direction orthogonale au plan de figure et de norme : $B=1.80T.$ 
 
L'ion $X^{+}$, animé de la vitesse $v'$ pénètre en $O_{3}$ dans cette zone suivant l'axe $O_{3}x.$
 
 
1) Rappeler l'expression de la force magnétique s'exerçant sur l'ion $X^{+}.$ 
 
Représenter sur un schéma le vecteur force pour que la déviation à partir de $O_{3}$ se fasse du côté positif de l'axe $O_{3}y.$ 
 
En déduire le sens du vecteur champ magnétique.
 
2) Démontrer que le mouvement de l'ion $X^{+}$ dans la zone $IV$ est plan et uniforme.
 
3) Montrer que l'ion $X^{+}$ décrit dans cette zone un arc de cercle, dont on établira l'expression littérale du rayon en fonction de $m$, $e$, $v'$ et $B.$
 
4) Exprimer le rayon du cercle trajectoire en fonction de $U'$, $m$, $e$ et $B.$
 
5) L'ion $X^{+}$ est recueilli au point $A$ tel que : $O_{3}A=0.069\,m.$
 
Trouver la masse de l'ion $X^{+}$ et identifier la substance $X.$

Exercice 4 : spectromètre de masse

Une source radioactive ponctuelle émet, suivant un axe $Ox$, un faisceau de particules passant entre les plaques horizontales d'un condensateur plan. 
 
L'action de la pesanteur est négligeable devant celle de la force de Lorentz. 
 
En l'absence de tout champ, les particules frappent en $O$ un écran situé à la distance a de la sortie du condensateur. 
 
On soumet alors le faisceau à un champ électrique uniforme et vertical $\overrightarrow{E}$, créé par le condensateur, et à un champ magnétique, uniforme, horizontal, perpendiculaire à l'axe $Ox$ et dirigé d'avant $\overrightarrow{B}$ en arrière.
 
 
a) Les particules entrent en $A$ dans le condensateur avec une vitesse parallèle à $Ox.$ 
 
Quelle doit être la valeur du champ $\overrightarrow{E}$ pour que les particules ne soient pas déviées ? 
 
Que se passe-t-il si $q$ change de signe ?
 
b) Le faisceau horizontal et monocinétique sortant en $A'$ du condensateur, est ensuite soumis à la seule action du champ magnétique et vient frapper l'écran au point $M$ tel que $OM=d.$
 
i) Montrer que les particules de même rapport $q/m$ décrivent des trajectoires circulaires uniformes de même rayon $R.$ 
 
Calculer $R.$ 
 
Quel effet a le signe de $q$ sur la déviation ?
 
ii) Montrer que $R=(d^{2}+a^{2})/2d.$ 
 
En déduire la valeur de $q/m.$
 
c) A.N. : on détecte des particules pour la valeur suivante des champs et de la déviation $d$ : $B=0$, $32T$ $E=6.4\cdot10^{6}Vm^{-1}$ ; $a=50\,cm$, $d=10\,cm$ vers le haut. 
 
Identifier ces particules sachant que pour l'électron $e=1.6\cdot10^{-19}C$, $m_{e}=9.1\cdot10^{-31}Kg$ et pour le proton et le neutron $m_{p}=m_{n}=1830\,m_{e}$

Exercice 5

Une particule de charge $q$, de masse $m$ traverse une chambre de Wilson dans laquelle règne un champ magnétique $B$ uniforme perpendiculaire au plan de la figure et orienté vers l'avant de ce plan. 
 
La particule ralentit en franchissant la surface $AB.$
 
Le cliché matérialisant la trajectoire permet de dire que la particule décrit des arcs de cercles de rayons $r_{1}$ et $r_{2}$ respectivement dans les parties $I$ et $II.$
 
 
1. Établir l'expression de $r_{1}$ et $r_{2}$ en fonction de $q$, $m$, $B$ et des vitesses respectives $v_{1}$ et $v_{2}$ de la particule. 
 
Dans quel sens se déplace la particule $($de $I$ vers $II$ ou de $II$ vers $I)$ ?
 
On donne : $r_{1}=\dfrac{r_{2}}{3}=14\,cm$
 
2. Quel est le signe de la particule ? 
 
Justifier la réponse
 
3. Calculer la charge massique $\dfrac{q}{m}$ et identifier la particule
 
On donne : 
 
$B=0.50T$ ; 
 
$v=2.0\cdot10^{7}m\cdot s^{-1}$ ; 
 
$m_{e}=9.1\cdot10^{-31}Kg$ ;
 
$m_{p}=1.67\cdot10^{-27}Kg$ ; 
 
$e=1.6\cdot10^{-19}C$

Exercice 6

Dans tout le problème, on négligera le poids de la particule devant les autres forces et on appliquera les lois de la mécanique classique
 
On envisage la séparation d'isotopes du Xénon $(Xe)$ au moyen d'un spectrographe de masse
 
Une chambre d'ionisation produit des ions positifs $_{54}^{129}Xe^{+}$ et $_{54}^{x}Xe^{+}.$ 
 
Ces ions sont ensuite accélérés entre deux plaques métalliques parallèles $P_{1}$ et $P_{2}$, puis à l'action d'un champ magnétique permet de les séparer
 
On donne : 
 
$e=1.6\cdot10^{-19}C$, 
 
$m_{n}=m_{p}=1.67\cdot10^{27}Kg$
 
 

1. Accélération des ions

Les ions traversent la plaque $P_{1}$ en $O_{1}$ sans vitesse initiale. 
 
Ils sont alors soumis entre $P_{1}$ et $P_{2}$ à une accélératrice $U=1000V$
 
a) Dans quel sens cette tension doit-elle être établie
 
b) Montrer que l'énergie cinétique, acquise par les ions lorsqu'ils traversent la plaque $P_{1}$ en $O_{1}$, est indépendante de l'isotope envisagé et cette valeur en joules
 
c) Calculer la vitesse acquise par les ions $_{54}^{129}Xe^{+}$ en $O_{2}.$
 
On assimilera la masse de l'ion à la somme des masses de ses nucléons
 
d) Exprimer en fonction de $x$ et $v$, la vitesse $v'$ acquise par les ions $_{54}^{x}Xe^{+}$ en $O_{2}$

2. Séparation des ions

Les ions, animés des vitesses $v$ et $v'$, pénètrent en $O$ dans une région où règne un champ magnétique $\overrightarrow{B}$ uniforme perpendiculaire au plan de la figure
 
a) On s'intéresse au mouvement des ions $_{54}^{129}Xe^{+}.$ 
 
Montrer que celui-ci est plan, circulaire et uniforme. 
 
Donner l'expression du rayon de courbure $R.$ 
 
Calculer $R$ pour $B=0.1T$
 
Les ions $_{54}^{129}Xe^{+}$ et $_{54}^{x}Xe^{+}$ décrivent un demi-cercle avant de tomber sur plaque photographique, respectivement en $A$ et $B$
 
b) On mesure la distance $AB=8\,cm.$ 
 
En déduire la valeur de $x\ (B=0.1T)$

Exercice 7

Pour identifier des ions désignés par $X_{1}$ ; $X_{2}$ ; $X_{3}$ et $X_{4}$, portant chacun une charge de valeur absolue $|q|=e$ on les introduit successivement dans une région où règne un champ magnétique $B$ uniforme avec la même vitesse $v_{0}.$ 
 
Les trajectoires obtenues sont représentées sur la figure suivante
 
 
1. Montrer que le mouvement d'une particule de masse $m$ et de charge $q$ de vitesse initiale $v_{0}$ perpendiculaire au vecteur champ magnétique uniforme $B$ est un mouvement uniforme circulaire. 
 
Puis montrer que : $$R=\dfrac{mV_{0}}{|q|B}$$
 
Donnée : 
 
la masse de l'ion d'un élément $^{A}X$ est : $m=Au$
 
2. En exploitant la figure :
 
2.1 Identifier le signe de la charge portée par chacun des ions $X_{1}$ ; $X_{2}$ ; $X_{3}$ et $X_{4}$ ?
 
2.2 Déterminer les rayons $R_{1}$ ; $R_{2}$ ; $R_{3}$ et $R_{4}$ de ces ions.
 
3. Identifier les ions $X_{1}$ ; $X_{2}$ ; $X_{3}$ et $X_{4}$ dans la liste suivante : 
 
$^{39}K^{+}$ ; $^{23}Na^{+}$ ; $^{35}Cl^{-}$ ; $^{19}F^{-}.$

Exercice 8

Un faisceau d'électrons émis par une cathode pénètre par le point $A$ de coordonnées $x_{A}=-0.20(m)$ ; $y_{A}=0$ avec une vitesse $\overrightarrow{V}_{0}=V_{0}\vec{j}$ dans une région où règne un champ magnétique uniforme $\overrightarrow{B}$ normal au plan $(Oxy)$ ou s'effectue le mouvement.
 
L'électron quitte le champ magnétique en $C$ avec une vitesse $\overrightarrow{V_{C}}$ pour aborder une zone où règne un champ électrostatique uniforme $\overrightarrow{E}$ pour en sortir au point $D$ de coordonnées $x_D=+0.20(m)$ ; $y_{D}=0$ avec une vitesse $\overrightarrow{V_{D}}$
 
1. Étude du mouvement de l'électron dans le champ $\overrightarrow{B}$
 
1.1 En appliquant la deuxième loi de Newton montrer que :
 
$-\ $ Le mouvement de l'électron est uniforme 
 
$-\ $ Le mouvement de l'électron est circulaire  
 
1.2 Donner l'expression du rayon $R$ de la trajectoire de l'électron 
 
1.3 Calculer la valeur de l'intensité de $\overrightarrow{B}$
  
1.4 Déterminer la durée  du mouvement de l'électron dans cette zone 
 
 
2. Étude du mouvement de l'électron dans le champ $\overrightarrow{B}$
 
On prend comme origine des dates $(t=0)$ l'instant d'arrivée de l'électron au point $C$
 
2.1 En appliquant la deuxième loi de Newton :
 
$-\ $ Établir les équations horaires du mouvement de l'électron 
 
$-\ $ En déduire l'équation de la trajectoire dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$
 
2.2 Calculer la valeur de l'intensité de $\overrightarrow{E}$
  
2.3 Déterminer la durée  du mouvement de l'électron dans cette zone 
 
Les données : on néglige l'effet du champ de pesanteur sur l'électron ; la charge de l'électron
 
$-e=-1.6\cdot10^{-19}C$ ; $V_{0}=10^{7}m\cdot s^{-1}$ ;
 
la masse de l'électron : $m=9.1\cdot10^{-31}kg$ ; les directions de $\overrightarrow{V_{0}}$ et celle de $\overrightarrow{V_{C}}$ font un angle de $\dfrac{\pi}{2}$ radian ; le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ est orthonormé

Exercice 9

Le spectrographe de masse est un dispositif utilisé pour la séparation des isotopes. 
 
Il est constitué :
 
$-\ $ d'une chambre (1) d'ionisation dans laquelle sont ionisés les isotopes à séparer,
 
$-\ $ d'une chambre (2) d'accélération des ions dans laquelle règne un champ électrique uniforme $\overrightarrow{E}$ créé par une tension $U_{0}$ appliquée entre deux plaques $(P_{1})$ et $(P_{2})$,
 
$-\ $ d'une chambre (3) hémicylindrique dans laquelle règne un champ magnétique uniforme $\overrightarrow{B}$,
 
$-\ $ d'un détecteur d'ions.
 
On se propose de séparer des isotopes de l'élément chlore.
 
On négligera dans tout l'exercice, le poids de l'ion chlorure devant les autres forces qui interviennent
 
 
1) a) Préciser le sens de pour que des ions négatifs, sortant de la chambre d'ionisation en $O_{1}$ avec une vitesse nulle, aient, dans la chambre d'accélération, un mouvement rectiligne accéléré suivant la direction $O_{1}O_{2}$ ? 
 
Justifier la réponse. 
 
b) Montrer qu'au point $O_{2}$, l'énergie cinétique est la même pour les différents types d'ions accélérés qui correspondent au même élément chimique et qui portent la même charge électrique. 
 
En est-il de même pour les vitesses ? 
 
Justifier la réponse.
 
2) Dans la chambre (3) règne un champ magnétique $\overrightarrow{B}$ normal au plan contenant $O_{1}$, $O_{2}$ et $I.$ 
 
Préciser son sens pour que des ions négatifs soient déviés vers un point d'impact $I$ du détecteur. 
 
3) Préciser la nature du mouvement d'une particule chargée dans chacune des chambres (2) et (3). 
 
4) Des ions chlorure $Cl^{-}$ sont accélérés sous une tension $U_{0}=500V.$
 
a) Déterminer l'intensité du champ magnétique $\overrightarrow{B}$ qui doit régner dans la chambre (3) pour que des ions $^{35}Cl^{-}$ viennent frapper le détecteur au point d'impact $I$ situé à $19cm$ de $O_{2}.$
 
b) Au niveau du détecteur et en un point $I'$ situé plus loin que $I$ du point $O_{2}$, on reçoit des ions négatifs désigné par $^{A}Cl^{-}.$ 
 
Sachant que la distance qui sépare le point $I$ du point $I'$ est $0.6cm$, déterminer le nombre de masse de l'ion $^{A}Cl^{-}$ considéré. 
 
c) Répondre par vrai ou faux aux propositions suivantes :
 
Dans un champ électrique uniforme, une particule chargée mobile suit toujours une trajectoire rectiligne.
 
Dans un champ magnétique uniforme, une particule chargée mobile suit toujours une trajectoire circulaire.
 
Développer, dans chaque cas, ce qui justifie la réponse.
 
On donne : 
 
Charge électrique élémentaire : $e=1.6\cdot10^{-19}C$ ; Unité de masse atomique : $u=1.66\cdot10^{-27}kg$

Exercice 10

Une particule injectée au cœur du cyclotron va être accélérée par le champ électrique alternatif de haute fréquence entre les « dés ». 
 
Puis, elle entre dans le « dé » suivant lorsque le champ électrique change de sens et elle est donc à nouveau accélérée, et ainsi de suite 
 
Sa trajectoire devient plus périphérique du fait de son augmentation d'énergie. 
 
Elle sera éjectée de l'accélérateur avec l'énergie adéquate à partir de cette dernière trajectoire, puis guidée et focalisée jusqu'à sa cible. 
 
1. Représenter, en justifiant, au point $A$ de la trajectoire de l'ion injecté dans le cyclotron, le vecteur vitesse $\overrightarrow{v}$ de l'ion et la force magnétique $\overrightarrow{F_{m}}$ qui s'exerce sur l'ion. 
 
Représenter le champ magnétique, $\overrightarrow{B}$ dans l'hypothèse où la charge $q$ de l'ion est positive. 
 
2. Montrer que l'action du champ $\overrightarrow{B}$ ne permet pas d'accroître l'énergie cinétique de l'ion. 
 
3. Démontrer que dans un $« D »$, dans l'hypothèse où le champ magnétique est uniforme et constant, le mouvement de l'ion est circulaire uniforme et exprimer le rayon de la trajectoire en fonction de $m$ (masse de l'ion), $v$ (module de la vitesse de l'ion), $q$ et $B.$
 
4. Montrer que la durée de passage dans un demi-cylindre, notée $t_{p}$ ne dépend pas de $v.$
 
Pour accroître l'énergie cinétique de l'ion, on utilise l'action du champ électrique $\overrightarrow{E}$ résultant de la tension $u$ appliquée entre les deux $« D ».$ 
 
On considère que pendant la durée très courte de passage de l'ion d'un $« D »$ à l'autre, la tension $u$ reste constante. 
 
5. Déterminer, en fonction de $q$ et $u$ les expressions des variations de l'énergie cinétique de l'ion lors de la traversée de l'espace entre les deux $« D ».$
 
6. Un ion est injecté dans la zone d'accélération avec une vitesse nulle. 
 
Quelle est sa vitesse $v_{1}$ au moment de la pénétration dans le premier $« D »$ et quel est le rayon $R_{1}$ de la première trajectoire semi-circulaire ? 
 
7. On peut négliger la durée de passage de l'ion dans l'intervalle entre les deux $« D »$ devant la durée de passage de l'ion dans un demi-cylindre. 
 
La tension $u$ est une fonction sinusoïdale du temps qui doit être synchronisée avec le mouvement des particules chargées de telle sorte que le champ électrique soit inversé à chaque demi-tour. 
 
Quelle doit être la fréquence d'oscillation de cette tension $u(t)$ permettant d'obtenir une accélération de l'ion à chaque passage dans l'intervalle entre les deux $« D ».$
 
8. Après chaque passage dans l'intervalle entre les deux $« D »$, la vitesse de la particule ainsi que le rayon $R$ de sa trajectoire dans un $« D »$ augmentent. 
 
Déterminer les suites $v_{k}$ et $R_{k}$, l'indice $k$ étant incrémenté d'une unité à chaque demi-tour.
 
9. Lorsque ce rayon finit par atteindre le rayon $R_{D}$ d'un $« D »$, l'ion est alors éjecté du cyclotron.
 
Exprimer en fonction de $m$, $q$, $B$ et $R_{D}$ l'énergie cinétique $E_{k}$ de l'ion lors de son éjection. 
 
10. Application numérique. 
 
Calculer, en joule, puis en $MeV$, l'énergie cinétique $E_{k}$ d'un ion zinc $Zn^{11+}$ sachant que : 
 
$B=1.67T$ ; $m=1.06\cdot10^{-25}kg$ ; $R_{D}=0.465m$ ; $e=1.60\cdot10^{-19}C$
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Généralité sur les champs magnétiques - Champs magnétique des courants - Ts

Classe: 
Terminale
 

Exercice 1

1) Représenter le spectre de l'aimant représenté ci-dessous.
 
 
2) On place au point $A$ un capteur de champ magnétique, de sensibilité : $20\,mV/mT.$
 
Celui-ci indique $227\,mV.$
 
a) Calculer l'intensité du champ magnétique au point $A.$
 
b) Tracer le vecteur champ magnétique en ce point.

Exercice 2

1) Tracer le spectre de l'aimant en $U$ entre les deux pôles.
 
 
2) Orienter les lignes de champ.
 
3) Identifier les pôles de cet aimant.
 
4) Quelle propriété possède le vecteur $B$ dans cette région de l'espace champ magnétique ?
 
Comment appelle-t-on un tel champ magnétique ?

Exercice 3

Soit un solénoïde de longueur $L=50\,cm$, constitué de $2000$ spires et parcouru par un courant d'intensité $1.5\,A.$
 
1) Identifier les pôles de ce solénoïde.
 
2) Calculer la norme du champ magnétique créé au centre de ce solénoïde.
 
3) Représenter le vecteur champ magnétique en ce point.
 
4) La norme du champ en $A$ est de $0.5\,mT.$
 
Représenter le vecteur champ magnétique en $A.$
 
 

Exercice 4

Deux aimants droits $A_{1}$ et $A_{2}$ sont placés sur l'axe $x'x.$ 
 
 
Chacun d'eux crée au point $M$ situé à égale distance des deux sources, un champ magnétique de $20\,mT.$
 
1) Représenter le vecteur champ magnétique en $M$, lorsque les deux pôles en regard sont de même nom.
 
2) Même question lorsque les deux pôles sont de noms différents.
 
3) On remplace l'aimant $A_{2}$ par une bobine $B_{2}.$
 
On désire qu'au point $M$ le champ résultant ait une norme égale à $60\,mT.$
 
Quelle doit être la norme du champ magnétique créé par la bobine ? 
 
(Deux cas sont envisageables).
 
Pour chaque cas, quel est le sens du courant dans la bobine ?

Exercice 5

 
Une bobine parcourue par un courant d'intensité $I$, crée en $M$ un champ magnétique de norme $B_{1}=2\,mT.$
 
Un aimant $A$ crée en $M$ un champ magnétique de norme $B_{2}=4\,mT.$
 
1) Représenter les vecteurs champ magnétique créés en $M$ par chacune des deux sources.
 
2) Représenter le vecteur champ magnétique résultant.
 
Déterminer sa norme.

Exercice 6

A l'intérieur d'un solénoïde $S_{1}$ comportant $n_{1}$ Spires par mètre, parcouru par un courant d'intensité $I_{1}$, on place un solénoïde $S_{2}$ dont l'axe est orthogonal à celui de $S_{1}$, comportant $n_{2}$ spires par mètre et parcouru par un courant $I_{2}.$
 
 
1) $I_{2}=0$ ; Représenter le vecteur induction magnétique $B_{1}$ au centre de $S_{1}$ et exprimer son intensité en fonction de $n_{1}$ et $I_{1}.$
 
2) $I_{2}\neq 0$ ; indiquer en le justifiant, le sens de $I_{2}$ pour que le vecteur induction $B_{2}$ crée au centre de $S_{2}$ ait le même sens que l'axe $(y'y).$
 
3) Une petite aiguille aimantée, placée au centre $O$ des deux solénoïdes prend une direction $\alpha$ avec l'axe $(x'x).$
 
a) Faire un schéma clair dans lequel sont représentés les vecteurs $B_{1}$, $B_{2}$ et l'aiguille.
 
b) Exprimer le rapport $n_{2}/n_{1}$ en fonction de $\alpha$, $I_{1}$ et $I_{2}.$
 
c) Calculer $n_{1}$ et $n_{2}$ sachant que $n_{1}+n_{2}=500\text{spires}\cdot m^{-1}.$ 
 
On donne $\alpha=63.2^{\circ}$ ; 
 
$I_{1}=2A$ et $I_{2}=1A.$
 
En déduire la valeur du champ résultant en $O.$

Exercice 7

La valeur de la composante horizontale du champ géomagnétique étant trop faible pour être mesurée à l'aide d'un tesla mètre courant, on se propose de la déterminer de la manière suivante.
 
On place une aiguille aimantée sur pivot vertical au centre $O$ d'un solénoïde long, à spires non jointives comportant $n=200$ spires par mètre, de manière à pouvoir observer l'orientation de l'aiguille. 
 
Le solénoïde est alors disposé horizontalement, et orienté pour que son axe soit perpendiculaire à celui de l'aiguille aimantée. 
 
On alimente le solénoïde avec un courant d'intensité suffisante pour produire un champ magnétique en $O$ de valeur $B_{S}.$ 
 
On constate que l'axe de l'aiguille aimantée est dévié d'un angle $\alpha.$
 
1) Indiquer sur le schéma suivant l'orientation de la boussole placée au point $O$ en absence de courant.
 
 
2) Représenter sans souci d'échelle sur le schéma ci-dessous, le vecteur $\overrightarrow{B_{S}}$ du champ magnétique crée par le courant électrique $i$ au centre $O$ du solénoïde. 
 
En déduire les faces nord et sud du solénoïde.
 
 
3) Une étude expérimentale consiste à mesurer la valeur de la déviation $\alpha$ de l'aiguille aimantée placée en $O$, pour différentes valeur de l'intensité du courant $i$ qui circule dans le solénoïde.
 
Les résultats obtenus ont permis de tracer la courbe ci-dessous.
 
 
a) Déterminer l'équation numérique de la courbe $\tan\alpha=f(i).$
 
b) Faire un schéma sur lequel on représentera les vecteurs $B_{H}$ et $B_{S}$ (sans souci d'échelle) au point $O.$
 
c) Trouver une relation entre la valeur de $B_{H}$ et $B_{S}$ et $\alpha.$
 
4) En déduire la valeur de la composante horizontale $B_{H}$ du champ géomagnétique.

Exercice 8

On dispose d'un solénoïde de longueur $L=40\,cm$ et comportant $N=250$ spires. 
 
On le place de telle sorte que son axe soit horizontal et perpendiculaire au plan du méridien magnétique. 
 
Le solénoïde est parcouru par un courant électrique d'intensité constante.

Partie I

Le champ magnétique terrestre peut être négligé.
 
On effectue des mesures de la valeur $BS$ du champ magnétique $B_{S}$ à l'intérieur du solénoïde. 
 
La sonde est placée sur l'axe du solénoïde à une distance $x$ de son centre $O.$ 
 
On obtient les résultats suivants :
$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x(cm)&0&4&8&11&14&17&20\\ \hline B_{S}(mT)&3.3&3.3&3.3&3.3&3.2&2.8&2.1\\ \hline \end{array}$$
 
1) Tracer un graphique représentant les variations de $B$ en fonction de $x$ sur toute la longueur du solénoïde.
 
2) Que peut-on dire du champ magnétique à l'intérieur de la bobine ?
 
3) Calculer l'intensité $I$ du courant qui traverse la bobine.
 
4) A l'aide du graphique, déterminer la longueur du solénoïde sur laquelle la valeur du champ magnétique reste supérieure à $90\%$ de sa valeur maximale.

Partie II

On fait maintenant diminuer l'intensité du courant dans les spires du solénoïde afin que la composante horizontale du champ magnétique terrestre ne soit plus négligeable. 
 
On a $I=0.1\,A.$
 
On place au centre de la bobine une petite aiguille aimantée. 
 
Celle-ci s'oriente spontanément dans une direction faisant un angle $\alpha=14.3^{\circ}$ avec l'axe du solénoïde.
 
1) On veut que le champ $B_{S}$ crée par la bobine soit dirigé vers la droite. 
 
Indiquer quel doit être le sens du courant dans les spires pour que ce soit effectivement le cas.
 
2) Faire un schéma représentant les vecteurs champs créés par le solénoïde $B_{S}$ et par la Terre $B_{H}$, ainsi que le champ résultant $B.$
 
3) Calculer la nouvelle valeur de $B_{S}.$

Exercice 9

1) Calculer l'intensité du champ magnétique $\overrightarrow{B}$ créé au point $M$ par les courants $I_{1}$ et $I_{2}$ qui traversent respectivement les fils rectilignes considérés comme infiniment longs. 
 
On donne : 
 
$I_{1}=I_{2}=I=6.0\,A$ et $d=12\,cm$
 
2) On néglige le champ magnétique terrestre. 
 
On place une petite aiguille aimantée au point $O$ ? 
 
Quelle orientation prend-elle ?
 
(Choisir ci-dessous la bonne réponse en justifiant la réponse)
 
 
Deux solénoïdes $(S_{1})$ et $(S_{2})$ comportant respectivement $n_{1}=400$ spires par mètre et $n_{2}=80$ spires par mètre, sont disposés de manière à avoir le même axe ; cet axe commun étant perpendiculaire au plan du méridien magnétique terrestre (figure ci-dessous).
 
On place un l'aiguille aimantée mobile autour d'un axe vertical, à l'intérieur des deux solénoïdes qu'on branche en série dans un circuit électrique. 
 
Lorsque le courant continu qui parcourt les deux solénoïdes a une intensité $I$, l'aiguille aimantée dévie de l'angle $\alpha=45^{\circ}.$
 
 
Déterminer la valeur de l'intensité $I.$ 
 
On distinguera le cas où la borne $(A_{1})$ est reliée à la borne $(B_{2})$ puis le cas où la borne $(A_{1})$ est reliée à la borne $(A_{2})$

Exercice 10

On étudie expérimentalement, à l'aide d'un teslamètre, l'intensité $B$ du champ magnétique à l'intérieur d'une bobine parcourue par un courant, en fonction de différents paramètres.
 
La bobine comporte $200$ spires, est longue de $40.0\,cm$, et a un diamètre de $5.0\,cm.$

I. Introduction

1. Décrire une méthode permettant de visualiser les lignes de champ de la bobine.
 
2. Quelles informations qualitatives peut-on tirer de l'observation des lignes de champ magnétiques quant à la nature de $Br$ à l'intérieur de la bobine ? 

II. Étude de l'influence du courant circulant dans la bobine

La sonde du teslamètre est placée au centre de la bobine. 
 
On fait varier l'intensité $I$ du courant dans la bobine et, pour chaque valeur de $I$, on note la valeur de $Br$
 
Le tableau ci-dessous comporte les valeurs de $I$ et $B$ obtenues : 
$$\begin{array}{|c|c|c|c|c|c|c|} \hline I(A)&0&1.5&2.5&3.5&4.5&5.0\\ \hline B(10^{-5}T&0&94&153&215&280&310\\ \hline \end{array}$$
 
1. Faire un schéma clair et annoté du montage à réaliser pour obtenir, faire varier, et mesurer l'intensité du courant $I$ dans le circuit de la bobine. 
 
2.1 Déterminer, à partir des données du tableau, la relation littérale entre $B$ et $I.$
 
2.2 Exprimer numériquement cette relation. 
 
3.1 Donner la relation théorique entre le champ $B$ et l'intensité $I.$
 
3.2 En déduire la valeur expérimentale de la perméabilité magnétique du vide $\mu_{0}$
 
3.3 Calculer l'erreur relative avec la valeur théorique. 

III. Étude de la valeur du champ magnétique le long de l'axe de la bobine

On maintient $I=4\,A$ dans la bobine. 
 
On mesure B en divers points le long de l'axe et à la distance $x$ du centre de la bobine. 
 
Le tableau ci-dessous donne les valeurs de $B$ en fonction de $x$ : 
$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x(cm)&0&4&8&12&14&16&18&20\\ \hline B(mT)&2.45&2.44&2.42&3.70&2.33&2.28&2.08&1.45\\ \hline \end{array}$$
 
1. Tracer la courbe représentant $B$ en fonction de $x.$ 
 
Commenter l'allure de la courbe. 
 
2. La courbe obtenue confirme-t-elle les informations obtenues à partir de l'observation des lignes de champ ? 
 
Justifier. 
 
3. Pour quelles valeurs de $x$ peut-on conclure que $B$ est constant à $5\%$ sur l'axe de la bobine ? 
 
Données : 
 
perméabilité magnétique du vide : $\mu_{0}=4\pi\cdot10^{-7}SI.$

Exercice 11

Mesure du champ magnétique terrestre
 
On souhaite mesurer la valeur du champ magnétique terrestre $B_{H}$, dont la valeur théorique dans le lieu de l'expérience est $B_{H}=2.0\cdot10^{-5}T.$
 
Pour cela, on dispose d'un solénoïde infiniment long de longueur $l=0.5\,m$, de section $S=80\,cm^{2}$, et comportant  $N=50$ spires. 
 
Les spires de ce solénoïde ne sont pas jointives, ce qui permet de voir   l'intérieur du solénoïde. 
 
On place en son centre une aiguille aimantée de façon à ce qu'elle soit perpendiculaire à la direction du champ magnétique $B_{S}$ créé par le solénoïde. 
 
Lorsque le solénoïde est parcouru par un courant d'intensité $I$, l'aiguille s'écarte de sa position initiale d'un angle $\alpha.$ 
 
Les angles obtenus pour différentes intensités sont rassemblés dans le tableau ci-dessous :
$$\begin{array}{|c|c|c|c|c|c|} \hline I(A)&0.1&0.2&0.3&0.4&0.5\\ \hline \alpha(\text{ en }^{\circ})&33&51&63&69&73\\ \hline \end{array}$$ 

I. Étude préalable du protocole expérimental

1. Rappeler les propriétés du champ magnétique à l'intérieur du solénoïde. 
 
Donner ses caractéristiques. 
 
2.1 De quels instruments de mesure a-t-on besoin pour faire les mesures ci-dessus ? 
 
2.2 Pourquoi a-t-on besoin de voir l'intérieur du solénoïde ? 
 
3. Selon quelle direction (Est-Ouest ou Nord-Sud) doit être disposé le solénoïde ? 
 
Justifier. 
 
4.1 Calculer le champ magnétique créé par le solénoïde en son centre, si celui-ci est parcouru par une intensité $I=10\,A.$
 
4.2 Pour quelle raison ne peut-on pas utiliser de telles intensités pour faire les mesures d'angles ? 
 
Combien vaudrait alors l'angle  

II. Exploitation des résultats

1.1 Faire un schéma « vu de dessus » de l'aiguille au centre du solénoïde lorsqu'elle est inclinée d'un angle $\alpha.$
 
Dessiner les vecteurs du champ magnétique terrestre $B_{H}$ et du champ magnétique créé par le solénoïde $B_{S}$
$$\alpha=arctan\left(\dfrac{\mu_{0}n\,I}{l\,B_{H}}\right)$$
 
1.2 Démontrer soigneusement que l'angle $\alpha$ est donné par l'expression : 
 
2.1 Tracer le graphique donnant la tangente de l'angle $\alpha$ $(\tan\alpha)$ en fonction de l'intensité $I.$
 
2.2 Calculer le coefficient directeur de la droite obtenue. 
 
2.3 En déduire la valeur du champ magnétique terrestre $B_{H}$
 
2.4 Calculer l'erreur absolue et l'erreur relative de votre mesure avec la valeur théorique.
 
Donnée : 
 
$\mu_{0}=4\pi\cdot10^{-7}SI.$

Exercice 12

On donne : 
 
$B_{H}=2\cdot10^{-5}T$ On prendra $4\pi=12.5$
 
1) Un solénoïde $S$, de centre $O$ et de longueur $L=62.5\,cm$, comportant $N=100$ spires, est parcouru par un courant électrique d'intensité constante $I=0.2\,A.$
 
a) Déterminer les caractéristiques du vecteur champ magnétique créé par le courant au point $O$ centre du solénoïde $S$
 
b) Sur la figure 2 (page 3 à compléter et à remettre avec la copie), 
 
Représenter le spectre magnétique créé par le courant à l'intérieur du solénoïde S et indiquer les faces de la bobine.
 
2) On place au point $O$ une petite aiguille aimantée mobile autour d'un axe vertical. 
 
Le solénoïde est placé de telle manière que son axe soit perpendiculaire au méridien magnétique.
 
a) Représenter sur la figure 3 (page 3 à compléter et à remettre avec la copie), les vecteurs $\overrightarrow{B}_{H}$ composante horizontale du vecteur champ magnétique terrestre et $\overrightarrow{B}_{C}$ le vecteur champ magnétique créé par le courant $I$ à l'intérieur du solénoïde en utilisant l'échelle : $1cm\ \rightarrow\ 10^{-5}T$, ainsi que la nouvelle position de l'aiguille aimantée.
 
b) Déterminer l'angle $\alpha$ que fait l'aiguille aimantée avec l'axe du solénoïde lorsque celle-ci prend une position d'équilibre stable.
 
3) On superpose avec les champs $\overrightarrow{B}_{C}$ et $\overrightarrow{B}_{H}$ un champ magnétique $\overrightarrow{B}_{a}$ créé par un aimant droit dont l'axe passe par $O$ et fait un angle $\theta=60^{\circ}$ avec l'axe du solénoïde. 
 
Le pôle nord de l'aimant se trouve à proximité du solénoïde (figure 4, page 3 à compléter et à remettre avec la copie). 
 
L'axe de l'aiguille aimantée s'oriente alors suivant une direction faisant un angle $\beta=45^{\circ}$ avec $\overrightarrow{B}_{H}.$ 
 
Montrer que la valeur du champ magnétique créé par l'aimant s'écrit sous la forme : 
$$B_{a}=\dfrac{B_{C}-B_{H}}{\sin\theta-\cos\theta}$$
 
Calculer sa valeur
 

 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Gravitation universelle - Ts

Classe: 
Terminale
 

Exercice 1

Un satellite artificiel de la Terre, de masse $m$, se déplace vitesse constante sur une orbite circulaire dans un référentiel galiléen lié au centre de la Terre à l'altitude $h=3.6\cdot10^{7}m$ compté à partir de la surface de la Terre. 
 
La trajectoire est située dans le plan équatorial et le satellite tourne dans le sens de rotation de la Terre.
 
Le rayon de la Terre est $R=6.4\cdot10^{6}m$
 
1. Calculer la valeur de l'intensité $g$ du champ de pesanteur à l'altitude $h$, sachant qu'à la surface de la Terre $g_{0}=9.8\,m\cdot s^{-2}.$ 
 
On rappelle la loi de la gravitation universelle $F=k\dfrac{Mm}{r^{2}}$0 où $M$ est la masse de la Terre et $r$ la distance du satellite au centre de la Terre.
 
2. Faire le bilan des forces appliquées au satellite supposé ponctuel et en déduire sa vitesse
 
3. Déterminer la période du mouvement dans le repère galiléen considéré ici.
 
 

Exercice 2

La Terre est assimilée à une sphère de rayon $T_{R}$ et de masse $M_{T}.$
 
Elle possède une répartition de masse à symétrie sphérique.
 
1. On suppose galiléen, le repère géocentrique dont l'origine coincide avec le centre de la Terre et dont les axes ont une direction fixe par rapport aux étoiles
 
Deux corps sphériques de masse $m_{1}$ et $m_{2}$, dont les centres sont distants de $r$ exercent l'un sur l'autre des forces d'attraction ayant pour intensité : $$F=G\dfrac{m_{1}m_{2}}{r^{2}}$$
 
$G$ est la constante de gravitation univerelle
 
1.1
 
1.1.1 Écrire l'expression de l'intensité $F_{0}$ de la force que la Terre exerce sur un corps ponctuel de masse $m=1Kg$ placé à surface
 
1.1.2 a) Déduire de la question 1.1.1, l'expression de la masse $M_{T}$ de la Terre en fonction de $g_{0}$, $R_{T}$ et $G$
 
b) Calculer $M_{T}$
 
On donne : 
 
$G=6.67\cdot10^{-11}S.I$, 
 
$g_{0}=9.8\,m\cdot s^{-2}$, 
 
$R_{T}=6370Km$
 
1.2 Montrer qu'a l'altitude $h$ au-dessus de la Terre, l'intensité du champ de gravitation est donnée par la relation : $$g=g_{0}\dfrac{R_{T}^{2}}{\left(R_{T}+h\right)^{2}}$$
 
$g_{0}$ est l'intensité du champ de gravitation terrestre au niveau du sol
 
2. Un satellite assimilé à un point matériel décrit une orbite circulaire dont son centre est confondu avec celui de la Terre.
 
Il est à l'altitude $h.$
 
2.1 Montrer que le mouvement du satellite est uniforme.
 
2.2 Établir en fonction $g_{0}$, $R_{T}$ et $h.$
 
2.2.1 la vitesse $v$ du satellite ;
 
2.2.2 La période $T$ du satellite ;
 
2.3 Calculer $v$ et $T$
 
2.4 On pose $r=R_{T}+h$
 
2.4.1 Montrer que le rapport $\dfrac{T^{2}}{r^{3}}=cte$ est égal à un constante.
 
C'est la $3^{e}$ de Kepler
 
2.4.2 Exprimer le rapport $\dfrac{T^{2}}{r^{3}}=cte$ en fonction de $M_{T}$ et $G$
 
2.4.3 Calculer la masse $M_{T}$ de la Terre.
 
Cette valeur est-elle compatible avec celle de la question 1.1.2 
 
On donne $h=300Km.$

Exercice 3

La terre est assimilée à une sphère homogène de centre $O$ de masse $M$ et de rayon $R.$ 
 
Le champ de gravitation crée par la Terre en tout point $A$ de l'espace situé à une distance $r$ du point $O$ est :
$$\overrightarrow{\mathfrak{G}}=-\dfrac{GM}{r^{2}}\overrightarrow{u}\quad\text{et}\quad\overrightarrow{u}=\dfrac{\overrightarrow{OA}}{\|\overrightarrow{OA}\|}$$
 
$G$ : Constante universelle de gravitation
 
1. Un satellite $(S)$ de masse $m$ décrit un mouvement uniforme sur une orbite circulaire de $r$ autour de la Terre.
 
Le mouvement est rapporté par rapport au repère géocentrique et on suppose que $(S)$ soumis à la seule action du champ de gravitation terrestre
 
1.1 Exprimer la vitesse $V$ de $(S)$ en fonction de l'intensité $G_{0}$ du champ de gravitation du sol, de $R$ et $r$
 
1.2 En déduire l'expression de la période $T$ du mouvement. 
 
Calculer $T$
 
On donne $R=6400Km$ ; 
 
$G_{0}=9.8\,m\cdot s^{-2}$ ; 
 
$r=8000Km$
 
2.
 
2.1 A partir du travail élémentaire $\mathrm{d}w=-f\mathrm{d}r$ de la force de gravitation exercée par la Terre sur le satellite ; montrer que le travail de cette force lors du déplacement du sol jusqu'à l'orbite de rayon $r$ est donné par : $$W=mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)$$
 
2.2 En déduire l'expression de l'énergie potentielle du système Terre-satellite en fonction de $G_{0}$, $m$, $r$ et $R.$
 
On choisira le niveau du sol comme étant de référence pour l'énergie potentielle
 
2.3 Exprimer l'énergie cinétique de $(S)$ en fonction de $G_{0}$, $m$, $r$ et $R$
 
En déduire l'expression de l'énergie mécanique $E$
 
3. Il se produit une très faible variation $\mathrm{d}r$ du rayon $r$, telle que la trajectoire puisse toujours être considéré comme circulaire
 
3.1 Exprimer la variation $\mathrm{d}v$ de la vitesse qui en résulte et montrer que $\mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r$ 
 
3.2 La variation de $\mathrm{d}r$ est en réalité due au travail $\mathrm{d}w_{f}$ des forces de frottements exercées par les couches raréfiées de l'atmosphère pendant le déplacement. 
 
Du signe de $\mathrm{d}w_{f}$, déduire l'effet de ces forces sur l'altitude et la vitesse de $(S).$

Exercice 4

On assimile le Soleil à une sphère de rayon $R_{S}$ et de masse $M_{S}$ présentant une répartition de masse à symétrie sphérique. 
 
On suppose que la trajectoire de la Terre autour du Soleil est un cercle de rayon $r.$
 
1. Donner l'expression littérale du champ de gravitation $G_{0S}$ à la surface du Soleil. 
 
Calculer sa valeur numérique.
 
2. Donner l'expression littérale du champ de gravitation $G_{S}$ en un point de l'orbite terrestre autour du Soleil. 
 
Calculer sa valeur numérique.
 
3. Comparer la valeur du champ de gravitation $G_{S}$ précédente à celle $G_{0}T$ du champ de gravitation terrestre au niveau du sol. 
 
Conclure.
 
Données :
 
$R_{S}=7.0\cdot10^{5}km$ 
 
$M_{S}=2.0\cdot10^{30}kg$ 
 
$r=1.5\cdot10^{8}km$
 
Constante de gravitation universelle : $G=6.67\cdot10^{-11}S.I.$
 
Champ de gravitation au niveau du sol : $G_{0}T=9.8\,N\cdot kg^{-1}$
 
Soit $M_{L}$ et $M_{T}$ les masses respectives de la Lune et de la Terre, ces astres étant supposés sphériques. 
 
Soit $R_{L}$ et $R_{T}$ leurs rayons. 
 
On a les relations $M_{T}=81\cdot M_{L}$ et $R_{T}=\dfrac{11}{3}R_{L}.$
 
4. Calculer la valeur du champ de gravitation lunaire $G_{0}L$ au niveau de son sol.
 
5. Il existe sur la ligne joignant les deux astres Terre et Lune un point où les champs de gravitation lunaire et terrestre se compensent.
 
a) Situer ce point $M$ remarquable en calculant sa distance $d$ au centre de la Terre.
 
b) Indiquer, sur le segment Terre-Lune, le domaine où l'action gravitationnelle d'un des deux astres est prépondérante.
 
Données : 
 
Distance Terre-Lune : $D=380\ 000\,km.$

Exercice 5

Données : 
 
Masse de la Terre $M_{T}=5.97\times 10^{24}kg$
 
Rayon de la Terre $R_{T}=6.38\times 10^{6}m$
 
Masse du Soleil $M_{S}=333\times 10^{3}\times M_{T}$
 
Constante universelle de gravitation $G=6.67\times 10^{-11}S.I.$
 
Valeur du champ de pesanteur au niveau du sol $g=9.81\,m/s^{2}$

1 Lancement d'un satellite

On étudie le lancement d'un satellite artificiel à partir d'un point $O$ de la surface terrestre.
 
1.a) Établir l'expression de la vitesse du point $O$ de la surface terrestre. 
 
Dans le référentiel géocentrique $R_{g}$ (assimilé ici à un référentiel galiléen) en fonction de la vitesse angulaire de rotation de la Terre autour de l'axe de ses pôles $($cette vitesse angulaire est notée $\Omega)$, du rayon terrestre $R_{T}$ et de la latitude $\lambda$ du lieu du lancement.
 
1.b) En déduire les conditions les plus favorables pour le lancement du satellite. 
 
Parmi les trois champs de tirs suivants, lequel choisir de préférence ?
 
Baïkonour au Kazakhstan $\lambda=46^{\circ}$ ;
 
Cap Canaveral aux USA $\lambda=28.5^{\circ}$ ;
 
Kourou en Guyane française $\lambda=5.23^{\circ}.$
 
1.c) Établir l'expression de l'énergie potentielle de gravitation d'un satellite en fonction de son altitude $z$ par rapport au sol. 
 
On prend pour référence une énergie potentielle nulle à l'infini. 
 
En déduire l'expression de l'énergie mécanique du satellite sur sa base de lancement dans le référentiel géocentrique.
 
1.d) On appelle ici vitesse de libération $v_{1}$, la vitesse verticale minimale qu'il faut communiquer initialement au satellite par rapport au sol, pour qu'il puisse se libérer de l'attraction terrestre. 
 
Donner l'expression de $v_{1}.$ 
 
Calculer sa valeur numérique dans le cas où le satellite est lancé de la base de Kourou (on tient donc compte de la rotation de la terre).

2. Satellite artificiel en orbite

On considère un satellite artificiel de masse $m$ en mouvement circulaire autour de la Terre.
 
2.a) Montrer que le mouvement du satellite est uniforme. 
 
Établir l'expression de la vitesse du satellite en fonction de son altitude ainsi que la troisième loi de Kepler liant la période de rotation $T$ du satellite au rayon $r$ de sa trajectoire.
 
2.b) Calculer le rayon de l'orbite d'un satellite géostationnaire .
 
2.c) Soit un satellite d'énergie mécanique initiale $Em_{0}.$ 
 
Son orbite est relativement basse et il subit donc les frottements des couches hautes de l'atmosphère. 
 
Il s'ensuit que l'énergie mécanique du satellite varie selon la loi :
 
$Em=Em_{0}(1+bt)$, $b$ étant un coefficient constant positif.
 
En supposant que la trajectoire reste approximativement circulaire.
 
Établir l'expression du rayon $r$ et de la vitesse $v$ du satellite en fonction du temps. 
 
Comparer les évolutions de $r$ et de $v$ ainsi que celles des énergies potentielle et cinétique. 
 
Que devient l'énergie perdue ?

Exercice 6

Pour mettre un satellite en orbite, une fusée $a$, au décollage, une poussée de $7.5\cdot10^{5}N.$ 
 
La masse totale de la fusée est de $40$ tonnes.
 
1. Quelle est l'accélération de la fusée ?
 
2. Le satellite est placé sur une orbite circulaire de rayon $r.$ 
 
Exprimer la vitesse $v$ et la période $T$ du mouvement du satellite en fonction de $K$, constante universelle de gravitation, $r$ et $M$, la masse de la terre. 
 
En déduire que $\dfrac{T^{2}}{R^{3}}=\text{constante}.$
 
3. La courbe reproduite en annexe donne la représentation graphique de $T^{2}$ en fonction de $r^{3}.$
 
Elle est obtenue à partir de données numériques sur la période $T$ et le rayon $r$ de quelques satellites qui tournent autour de la Terre. 
 
Déduire de la courbe la valeur de la masse $M$ de la Terre.
 
$K=6.67\cdot10^{-11}U.S.I.$
 
4. Le satellite est placé sur une orbite de rayon $r$, contenu dans le plan équatorial.
 
a) Exprimer les énergies potentielles $E_{P}$, $E_{C}$ et totale $E_{T}$ du satellite en fonction de la masse $M$ de la Terre, de la masse $m$ du satellite et de $r.$ 
 
$« E_{P}$ est nulle lorsque le satellite est infiniment éloigné de la Terre $».$
 
b) Avant d'être placé sur son orbite de rayon $r$, le satellite, était posé sur le sol, en un point $P$ de latitude $\gamma.$ 
 
Sa vitesse était, la vitesse $V_{e}$ due à la rotation de la Terre, supposée sphérique de rayon $R.$ 
 
Donner l'expression de $V_{e}$ en fonction de $ω_{T}$, vitesse angulaire de rotation de la Terre, $R$ et $\gamma.$ 
 
Déterminer les expressions des énergies potentielles $E_{P1}$, cinétique $E_{C1}$ et totale $E_{T1}$ du satellite au point $P.$
 
5. a) Pour placer le satellite sur son orbite, il a fallu lui fournir l'énergie $\Delta E=E_{T}-E_{T1}.$
 
Montrer que $\Delta E$ varie avec $\gamma.$
 
b) On considérera que le satellite tourne dans le même sens que la Terre. 
 
Où doit-on choisir les bases de lancement pour l'énergie $\Delta E$ soit minimale ?
 
6. La première vitesse cosmique $V_{1}$ est la vitesse de satellisation circulaire à basse altitude autour de la Terre d'un engin spatial. 
 
Calculer $V_{1}$ à l'altitude $h=100\,km.$
 
On donne $R=6400\,km$ et la masse $M$ de la Terre.
 
 

Exercice 7

Un satellite supposé ponctuel, de masse $m_{S}$, décrit une orbite circulaire d'altitude $h$ autour de la Terre assimilée à une sphère de rayon $R_{T}.$ 
 
On fera l'étude dans un référentiel géocentrique considéré comme galiléen.
 
1. Établir l'expression de l'intensité $g$ du vecteur champ de pesanteur à l'altitude $h$ en fonction de sa valeur $g_{0}$, au niveau du sol, de $R_{T}$ et de $h.$
 
2. Déterminer l'expression de la vitesse $v_{S}$ du satellite, celle de sa période et de son énergie cinétique.
 
Application numérique : 
 
$m_{S}=1020\,kg$ ; 
 
$g_{0}=9.81\,m/s^{2}$ ; 
 
$R_{T}=6400\,Km$ ; 
 
$h=400\,km.$
 
3. L'énergie potentielle du satellite dans le champ de pesanteur à l'altitude $h$ est donnée par la relation : 
$$E_{P}=-\dfrac{Km_{S}M_{T}}{R_{T}+h}$$ avec $K$, constante de gravitation et $M_{T}$ masse de la Terre et en convenant que $E_{P}=0$ pour $h_{P\infty}.$
 
Justifier le signe négatif et exprimer $E_{P}$ en fonction de $m_{S}$, $g_{0}$, $R_{T}$ et $h.$ 
 
Déterminer l'expression de l'énergie mécanique $E$ du satellite puis comparer $E_{P}$ à $E_{C}$ et $E$ à $E_{C}.$
 
4. On fournit au satellite un supplément d'énergie $\Delta E=+5\cdot10^{8}J.$
 
Il prend alors une nouvelle orbite circulaire. 
 
Déterminer :
 
a) Sa nouvelle énergie cinétique et sa vitesse
 
b) Sa nouvelle énergie potentielle et son altitude.

Exercice 8

Le $15$ octobre $1997$, le véhicule spatial Cassini emportait à son bord la sonde HUYGENS destinée à l'exploration des anneaux de Saturne.
 
Titan, le plus gros satellite de Saturne, a été découvrent en $1665$
 
On étudie le mouvement supposé circulaire de Titan dans le référentiel centré sur Saturne et dont les trois axes sont dirigés vers trois étoiles lointaines supposées fixes
 
1. Reproduire le schéma ci-dessus et représenter qualitativement la force gravitationnelle qui agit sur Titan
 
2. Donner l'expression vectorielle de cette force
 
3. Établir du vecteur accélération du centre d'inertie de Titan sur son orbite et le représenter qualitativement sur le schéma précédent
 
4. Montrer que le mouvement de Titan sur son orbite est uniforme
 
5. Établir en fonction de $G$ $M_{S}$ et $r_{T}$ :
 
5.1 l'expression de la vitesse $V_{T}$ du centre d'inertie de Titan
 
5.2 l'expression de la période de révolution $T_{T}$ de Titan autour de Saturne
 
6. Montrer qu'au cours de sa révolution autour de Saturne :
 
$\dfrac{T_{T}^{2}}{r_{T}^{3}}=K=\text{constante}$ $(3^{e}$ loi de Kepler$)$
 
7. En fait Saturne possède un cortège de satellites dont au moins $60$ ont été identifiés à ce jour.
 
Parmi eux, figurent Rhéa et Dioné découverts par Jean Dominique Cassini respectivement en $1672$ et $1684$
 
7.1 Montrer que ces deux satellites vérifient la $3^{e}$ loi de Kepler
 
7.2 En déduire la masse $M_{S}$ de Saturne
 
On donne :
 
$-\ $ Constante de gravitation universelle $G$ : $G=6.67\cdot10^{-11}S.I$
 
$-\ $ Rayon de l'orbite de Rhéa $r_{R}=527070\,Km$
 
$-\ $ Période de révolution de Rhéa autour de Saturne $T_{R}=4.518\,jours$ soit $390355\,s$
 
$-\ $ Rayon de l'orbite de Dioné $r_{D}=377400\,Km$
 
$-\ $ Période de révolution de Dioné autour de Saturne $T_{D}=2.737\;jours$ soit $236477\,s$
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Série d'exercices : Dynamique - Ts

Classe: 
Terminale
 

Exercice 1

Dans ce problème on prendra $g=10\,m\cdot s^{-2}.$ 
 
Tous les calculs seront effectués à $10^{-2}$ près.
 
Un solide $(S)$ de masse $m=50\,g$, de dimension négligeable, peut glisser sur une piste $ABCD$ située dans un plan vertical :
 
$-\ $ $AB$ est la ligne de plus grande pente d'un plan incliné d'un angle $\alpha=30^{\circ}$ par rapport à l'horizontale ; $AB=1.6\,m.$
 
$-\ $ $BCD$ est le quart d'un cercle de centre $I$ et de rayon $r=0.9\,m$ ; $C$ est situé sur la verticale passant par $I$ (voir figure).
 
1) On néglige les frottements. 
 
Le solide $(S)$ part du point $A$ sans vitesse.
 
a) Calculer sa vitesse en $B$, en $C$ et en $D.$
 
b) Calculer l'intensité de la force $\overrightarrow{R}$ exercée par la piste sur le solide $(S)$ en $C$ et en $D.$
 
c) Donner les caractéristiques du vecteur vitesse $\overrightarrow{V_{D}}$ du solide $(S)$ au point $D.$
 
2) On néglige la résistance de l'air. 
 
A partir du point $D$, le solide $(S)$ tombe dans le vide avec la vitesse $\overrightarrow{V_{D}}$ précédente. 
 
Le point $C$ est situé à la hauteur $h=1.55\,m$ du sol horizontal.
 
a) Donner l'équation cartésienne de la trajectoire du mouvement de $(S)$ à partir du point $D$, dans le repère $(O\;,\ x\;,\ z).$
 
b) Jusqu'à quelle hauteur $H$ au-dessus du sol horizontal monte le solide $(S)$ ?
 
c) Calculer la distance $OP$ où $P$ est le point d'impact du solide $(S)$ sur le sol horizontal.
 
3) Dans cette question, la piste exerce au mouvement du solide $(S)$ une force de frottements $\overrightarrow{f}$ parallèle et de sens contraire à sa vitesse à chaque instant, et d'intensité constante le long de $ABCD.$ 
 
Partant de $A$ sans vitesse, le solide $(S)$ s'arrête au point $D.$
 
a) Établir en fonction de $m$, $g$, $R$ et $\alpha$, l'expression algébrique du travail $W_{\overrightarrow{f}}$ de la force de frottements entre les points $A$ et $D.$ 
 
Calculer $W_{\overrightarrow{f}}$
 
b) En déduire l'intensité de la force $\overrightarrow{f}$
 
On donne : $\cos 30^{\circ}=0.86.$
 
 

Exercice 2

Un avion de guerre supersonique est animé d'un mouvement rectiligne uniforme à la vitesse $V_{0}=400\,m\cdot s^{-1}$ vole à une altitude de $2000\,m$, son radar a détecté un véhicule de transport de soldats ennemis supposé ponctuel, immobile au point $A$, le pilote a décidé de les attaquer, malgré l'interdiction de ce fait par la loi de Genève. 
 
 
En passant par $O$ origine du repère l'avion $(O\;,\ \vec{i}\;,\ \vec{j})$, a lâché, à une date prise comme origine de temps, une bombe qui après quelques secondes adétériorécomplètement le véhicule et a tué tous les soldats.
 
En négligeant la force résistance de l'air et en appliquant la relation fondamentale de la dynamique à la bombe déterminer les composantes selon l'axe $(0\;,\ x)$ et selon l'axe $(O\;,\ y)$ de son accélération.
 
1) Établir les lois horaires de mouvement de la bombe selon les deux axes.
 
2) En déduire l'équation de la trajectoire de la bombe relativement au repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
 
3) A quelle distance de la verticale passant par $O$ se trouvait le véhicule ? 
 
Déterminer la date d'arrivée de la bombe au véhicule.
 
4) Où se trouvait l'avion à la date d'arrivée de la bombe au véhicule ?
 
Déterminer les caractéristiques du vecteur vitesse de la bombe lorsqu'elle se trouvait à $1000\,m$ au-dessus du sol.

Exercice 3

Dans tout le problème, on néglige les frottements et on prend pour l'intensité de pesanteur $g=10\,m\cdot s^{-2}.$
 
Un pendule simple est constitué par une bille ponctuelle $M_{1}$ de masse $m_{1}=200\,g$ suspendue au bout d'un fil inextensible de masse négligeable et de longueur $\ell=0.9\,m.$
 
1) On écarte le pendule d'un angle $\alpha$ par rapport à sa position d'équilibre verticale et on le lâche sans vitesse initiale. 
 
La vitesse de la bille $M_{1}$ lors de son passage à la position
d'équilibre est $v=3\,m\cdot s^{-1}.$ 
 
Calculer la valeur de l'angle $\alpha.$
 
2) Lors de son passage à la position d'équilibre la bille $M_{1}$ heurte, au cours d'un choc parfaitement élastique, une autre bille ponctuelle $M_{2}$ immobile de masse $m_{2}=100\,g.$ (figure)
 
2) La vitesse de la bille $M_{2}$, juste après le choc, est $v_{A}=4\,m\cdot s^{-1}.$ 
 
Calculer la vitesse de la bille $M_{1}$ juste après le choc en appliquant la conservation de la quantité de mouvement.
 
3) La bille $M_{2}$ est propulsée avec la vitesse $V_{A}$ sur une piste qui comporte trois parties :
 
$-\ $ Une partie horizontale $AB$,
 
$-\ $ Une certaine courbe $BC$,
 
$-\ $ Un arc de cercle $CD$, de rayon $r$ et de centre $O.$
 
Les points $O$, $A$, $B$ et $E$ se trouvent dans un même plan horizontal.
 
a) Exprimer, en fonction de $g$, $r$, $\beta$ et $v_{A}$, la vitesse de la bille $M_{2}$ au point $I$
 
b) Exprimer, en fonction de $m_{2}$, $g$, $r$, $\beta$ et $v_{A}$, l'intensité de la réaction de la piste sur la bille $M_{2}$ au point $I.$
 
c) La bille $M_{2}$ arrive au point $D$ avec une vitesse horizontale de valeur $v_{D}=1\,m\cdot s^{-1}.$ 
 
Calculer la valeur de $r.$
 
4) Arrivée au point $D$, la bille $M_{2}$ quitte la piste avec la vitesse $\overrightarrow{V_{D}}$  précédente et tombe en chute libre.
 
a) Établir l'équation cartésienne de la trajectoire de la bille $M_{2}$ dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
 
b) Calculer la distance $OE.$
 
 

Exercice 4

Dans tout l'exercice, on suppose que le mouvement des protons a lieu dans le vide. 
 
Et on néglige leur poids devant les autres forces. 
 
On considère le dispositif de la figure ci-dessous.
 
Des protons sont émis en $C$ avec une vitesse quasiment nulle, puis accélérés entre les points $C$ et $D$ des plaques $P_{1}$ et $P_{2}$
 
1. Préciser le signe de la tension $U_{CD}$ pour que les électrons soient accélérés. 
 
Justifier votre réponse.
 
2. On posera par la suite $|U_{CD}|=U$
 
2.1 Exprimer la vitesse d'un proton en $D$ en fonction de $U$, $e$ et $m_{p}$
 
2.2 Calculer cette vitesse.
 
3. Après la traversée de la plaque $P_{1}$ en $D$, les électrons pénètrent en $O$ entre deux plaques parallèles $P_{3}$ et $P_{4}$ de longueur $l$ et distantes de $d.$ 
 
La tension $U'$ appliquée entre ces plaques crée un champ électrostatique $\overrightarrow{E}$ uniforme.
 
On donne $l=20\,cm$ et $d=7\,cm.$
 
3.1 Montrer que l'énergie cinétique se conserve entre $D$ et $O.$
 
3.2 Établir dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ les équations du mouvement d'un proton dans la région limitée par les deux plaques $P_{3}$ et $P_{4}$
 
3.3 Vérifier que l'équation de la trajectoire peut s'écrire :$$y=-\dfrac{U'}{4dU}x^{2}$$
 
3.4 Déterminer la condition à laquelle doit satisfaire la tension $U'$ pour que les protons sortent du champ électrostatique $\overrightarrow{E}$ sans heurter la plaque $P_{4}$
 
3.5 Déterminer $U'$ pour que les protons sortent du champ en passant le point $S$ de coordonnées $\left(l\;,\ -\dfrac{d}{5}\right)$
 
4. A la sortie du champ électrostatique par le point $S$, les protons sont reçus en $J$ sur un écran plat $E$ placé perpendiculairement à l'axe $Ox$
 
4.1 Représenter qualitativement la trajectoire d'un proton entre $O$ et $J$
 
4.2 Établir l'expression littérale de la déviation $O'J$ du spot sur l'écran
 
4.3 Calculer la distance $O'J.$
 
On donne : 
 
$L=20\,cm$ ; 
 
$U=10^{3}V$ ; 
 
masse du proton : $m_{p}=1.67\cdot10^{-27}kg$ ;
 
$OI=\dfrac{l}{2}$ 
 
Charge élémentaire : $e=1.6\cdot10^{-19}C$
 
 

Exercice 5

 
Un dispositif permet de lancer une bille à la vitesse $v_{0}=16\,m\cdot s^{-1}.$
 
La bille part d'un point $O$, vers le haut, suivant une direction faisant l'angle $\alpha$ avec la verticale.
 
1) Déterminer les lois horaires du mouvement.
 
2) Quelle est l'équation de la trajectoire ?
 
3) a) Pendant combien de temps la bille s'élève-t-elle avant de descendre ?
 
b) Quelle est sa vitesse à la fin de cette phase ascendante ? $(\alpha=50^{\circ})$
 
4) Quelle est l'altitude maximale atteinte par la bille, comptée à partir de son point de départ $O$ ?
 
La bille retombe sur l'axe $Ox$ en $P.$
 
5) a) Déterminer la distance $OP.$
 
b) Pour quelle valeur de $\alpha$, $OP$ est-elle maximale ?
 
Soit $Q$ un point de l'axe $Ox$ d'abscisse $x_{0}=10\,m.$
 
6) Montrer qu'il y a deux angles de tir $\alpha_{1}$ et $\alpha_{2}$ permettant d'atteindre $Q.$
$$\left(\dfrac{1}{\sin^{2}\alpha}=\dfrac{\sin^{2}\alpha+\cos^{2}\alpha}{\sin^{2}\alpha}=1+cot\,g^{2}\alpha\right)$$

Exercice 6

Une balle $B$ de mini-golf est poussée en $A$ à l'aide d'un club. 
 
La balle, supposée ponctuelle, dévale la pente $AC$ et décolle en $C$ où elle commence alors un mouvement aérien vers le trou noté $T.$
 
On se propose d'étudier le mouvement de la balle $B$ dans le repère $(O\;,\ x\;,\ z)$ supposé galiléen.
 
Dans tout l'exercice, on ne considèrera aucune force liée à l'atmosphère.
 
On précise que $z_{C}=40\,cm$ et $g=9.8\,N\cdot kg^{-1}.$
 
 
I. La trajectoire balistique de $C$ vers $T.$
 
La balle quitte le point $C$ de la rampe à la date $t=0s$ avec une vitesse $v_{0}$ horizontale égale à $2.0\,m\cdot s^{-1}.$
 
a) Qu'est-ce qu'un référentiel galiléen ?
 
b) Faire le bilan des forces qui s'exercent sur la balle lors de cette phase. 
 
Conclure.
 
c) Établir les équations horaires de la vitesse et de la position de la balle $B.$
 
d) En déduire l'équation $z(x)$ de la trajectoire de la balle $B.$
 
e) Quel doit être alors l'abscisse $x_{T}$ du trou $T$ pour que la balle tombe directement dedans ?
 
f) Déterminer la date $t_{F}$ à laquelle la balle $B$ tombe dans le trou.
 
II. Le mouvement sur la rampe
 
La balle quitte le point $A$ avec une vitesse de $0.80\,m\cdot s^{-1}.$
 
a) Déterminer la hauteur $z_{A}$ de $A$ nécessaire pour que la balle arrive en $C$ avec la vitesse de $2.0\,m\cdot s^{-1}.$
 
b) Expliquer pourquoi la vitesse $v_{0}$ est parfaitement horizontale lorsque la balle quitte le point $C.$

Exercice 7

Lors d'un match de basket, pour marquer un panier, il faut que le ballon passe dans un cercle métallique situé dans un plan horizontal, à $3\,m$ du sol. 
 
On assimile le ballon à un point matériel qui doit passer exactement au centre $C$ du cercle métallique. 
 
$xOy$ est un plan vertical contenant le point $C$ ; $xOz$ est le plan du sol supposé horizontal.
 
1) D'un point $A$ de $Oy$ situé à $2\,m$ du sol, un basketteur, sans adversaire, lance le ballon, avec une vitesse $\overrightarrow{V_{0}}$ contenue dans le plan
 
 
$xOy$ et dont la direction fait un angle $\alpha=45^{\circ}$ avec un plan horizontal.
 
On négligera l'action de l'air et on prendra $g=10\,m\cdot s^{-2}.$
 
a) Montrer que la trajectoire est plane.
 
b) Établir l'équation de cette trajectoire dans le système d'axes indiqué, en fonction de la valeur $V_{0}$ de la vitesse initiale.
 
c) Quelle doit être la valeur de $V_{0}$ pour que le panier soit réussi, sachant que les verticales de $A$ et de $C$ sont distantes de $7.1\,m$ ?
 
d) Quelle est la durée du trajet effectué par le ballon du point $A$ au point $C$ ?
 
2) Voulant arrêter le ballon, un adversaire situé à $0.9\,m$ du tireur, saute verticalement en levant les bras. 
 
La hauteur atteinte alors par ses mains est de $2.7\,m$ au-dessus du sol.
 
$\alpha$ et $V_{0}$ ayant les mêmes valeurs que précédemment, le panier sera-t-il marqué ?

Exercice 8

Les parties $(A)$ et $(B)$ sont indépendantes. 

On donne $g=10\,m\cdot s^{-2}.$
 
A. Dans cette partie les frottements sont supposés négligeables.
 
A l'origine des dates, un solide $S_{1}$ supposé ponctuel, de masse $m_{1}=200\,g$ est lâché sans vitesse initiale en un point $A$ d'un plan incliné (fig 1) dont la ligne de plus grande pente fait un angle $\alpha=30^{\circ}$ avec l'horizontale. 
 
 
Le solide $(S_{1})$ glisse sans frottement et arrive au point $B$, à la date $t_{B}$, ayant la vitesse $V_{B}.$
 
1) a) Représenter les forces exercées sur le solide $(S_{1})$
 
b) Établir l'expression de son accélération $a$, déduire la nature de son mouvement.
 
Calculer la valeur de $a.$
 
2) a) Calculer la valeur de la vitesse $V_{B}$ sachant que la distance $AB=2.5\,m.$
 
b) Calculer la durée $t_{B}$ du trajet $AB.$
 
B. Dans cette partie les frottements ne sont plus négligeables
 
Dans cette partie on relie le solide $(S_{1})$ à un solide $(S_{2})$ de masse $m_{2}=m_{1}$ par un fil inextensible, de masse négligeable, qui passe sur la gorge d'une poulie $(P)$ à axe fixe, dont on néglige la masse. 
 
A l'origine des dates $(t=0)$, $(S_{1})$ part de $B$ vers $A$ sans vitesse initiale. 
 
Au cours de son mouvement $(S_{1})$ est soumis à une force de frottement $\overrightarrow{f}$ supposée constante, parallèle à la ligne de plus grande pente du plan incliné et de sens opposé au mouvement. (fig 2)
 
 
1) a) En appliquant la deuxième loi de Newton $(R.F.D)$ au système, établir l'expression de son accélération $a$ et déduire la nature du mouvement.
 
b) Sachant que la valeur de $f$ est égale à $0.2\,N$, calculer $a.$
 
2) A l'instant de date $t_{C}=1\,s$, le solide $(S_{1})$ arrive en $C$ à la vitesse $V_{C}.$ 
 
Calculer $V_{C}.$
 
3) Au passage du solide $(S_{1})$ par le point $C$, le fil est coupé.
 
a) Donner l'expression de la nouvelle accélération $a_{1}$ du solide $(S_{1})$ après la coupure du fil, déduire la nature de son mouvement.
 
b) Calculer la distance maximale $($par rapport au point $C)$ parcourue par le solide $(S_{1})$ après la coupure du fil.
 

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

 
Auteur: 
Amary Thiam & Sidy Mouhamed Ndiaye

Pages