La glutaminylalanine, dipeptide formé à partir de la glutamine et de l'alanine, est un produit de dégradation incomplète de la digestion des protéines. 

 

Il est connu pour avoir des effets physiologiques.

 

1.1 La molécule du dipeptide.

 

La molécule de la glutaminylalanine est représentée par la formule semi-développée ci-dessous :

 

 

 

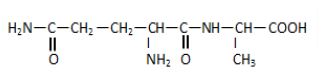
1.1.1. Recopier la formule. 

 

Encadrer les groupes fonctionnels et les nommer. $(0.75\;pt)$

 

1.1.2. Repérer la liaison peptidique. $(0.25\;pt)$

 

1.1.3 Repérer par un astérisque $(\ast)$ les atomes de carbone asymétriques dans la molécule. $(0.25\;pt)$

 

1.2. Étude de l'acide $\alpha-aminé\ N-terminal\ du\ dipeptide$

 

La glutamine, l'acide $\alpha$-aminé $N$-terminal du dipeptide, est l'acide aminé le plus abondant dans le sang et dans les muscles. 

 

Le corps est capable de synthétiser lui-même la $L$-glutamine que l'on retrouve aussi dans la viande, le poisson, les produits laitiers, les céréales et les légumineuses. 

 

Parmi les rôles de la $L$-glutamine, on peut citer l'amélioration des performances physiques, la réduction de la sensation de la fatigue chez les joueurs de football...

 

1.2.1. Définir un acide $\alpha$-aminé. $(0.25\;pt)$

 

1.2.2. Montrer que la molécule de glutamine est chirale. $(0.25\;pt)$

 

1.2.3. Donner la représentation de Fisher de la $L$-glutamine $(0.25\;pt)$

 

1.3 Étude de l'acide $\alpha$-aminé $C$-terminal du dipeptide

 

L'alanine, l'acide $\alpha$-aminé $C$-terminal de la glutaminylalanine, est aussi un acide aminé qui se retrouve dans les mêmes sources alimentaires que la glutamine. 

 

Elle fait augmenter le taux de sucre dans le sang et contribue à la formation des globules blancs, elle est donc indispensable au maintien d'une bonne santé.

 

1.3.1. En solution aqueuse la molécule d'alanine se présente sous forme d'un ion dipolaire entre autres espèces chimiques. 

 

Donner la formule et le nom de cet ion. $(0.5\;pt)$

 

1.3.2. Écrire l'équation-bilan de la réaction de l'ion dipolaire en milieu très acide puis en milieu très basique. 

 

Quels sont les couples acide-base auxquels participe l'ion dipolaire ? $(0.75\;pt)$

 

1.3.3 Les $pKa$ des couples précédents valent $2.3$ et $9.9.$ 

 

Proposer un diagramme de prédominance des espèces d'une solution aqueuse d'alanine. $(0.5\;pt)$

L'éthanamine ou éthylamine, de formule $C_{2}H_{5}NH_{2}$ , est un composé organique azoté. 

 

Elle est utilisée comme solvant et comme matière première dans la synthèse de colorants et d'insecticides.

 

On se propose de vérifier que l'éthanamine est une base faible et de réaliser le dosage acido-basique d'une solution d'éthanamine.

 

2.1. Basicité de l'éthanamine.

 

Dans une première expérience, on mesure le $pH$ d'une solution aqueuse d'éthanamine de concentration molaire volumique $C_{b}=1.25\cdot10^{-2} mol\cdot L^{-1}.$ 

 

On trouve $pH=11.4.$

 

2.1.1 Ces données prouvent-elles que l'éthanamine est une base faible ?

 

Justifier la réponse. $(0.5\;point)$

 

2.1.2 Écrire l'équation-bilan de la réaction de l'éthanamine avec l'eau.$(0.25\;point).$

 

2.1.3. Faire l'inventaire des espèces chimiques présentes dans la solution aqueuse d'éthanamine et déterminer leurs concentrations molaires volumiques. 

 

En déduire le $pka$ du couple $C_{2}H_{5}NH_{3}^{+}/C_{2}H_{5}NH_{2}$

 

Le produit ionique de l'eau est $K_{e}=10^{-14}.$ $(01\;point)$

 

2.2. Étude du dosage de l'éthanamine.

 

Dans une deuxième expérience, on effectue le dosage $pH-métrique$ d'un volume $V'_{b}=50\;cm^{3}$ de la solution d'éthanamine précédente par une solution d'acide chlorhydrique de concentration $C_{a}=0.02\;mol\cdot L^{-1}.$

 

On obtient le tableau de mesures suivant :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline V_{a}\left(cm^{3}\right)&0&4&8&12&16&20&24&26&27&28&29&30&31\\ \hline pH&11.4&11.20&11.05&10.90&10.75&10.55&10.30&10.15&10.05&9.95&9.85&9.65&9.45\\ \hline \end{array}$$

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline 32&32.2&32.5&32.7&33&34&35&36&38&40&44&48\\ \hline 8.95&8.75&6.45&4.30&3.90&3.45&3.20&3.10&2.90&2.80&2.60&2.50\\ \hline \end{array}$$

 

2.2.1. Faire un schéma annoté du dispositif de dosage. $(0.25\;point)$

 

2.2.2. Écrire l'équation-bilan de la réaction support du dosage. $(0.25\;point)$

 

2.2.3. Tracer la courbe $pH=f(V_{a}).$ 

 

Échelles : $1\;cm$ pour $1$ unité de $pH$ et $1\;cm$ pour $2\;cm^{3}.$ $(0.75\;point)$

 

2.2.4. Déterminer graphiquement le point d'équivalence $E$ $\left(V_{a}E\;,\ pHE\right).$ $(0.5\;point)$

 

2.2.5. Quelle valeur de la concentration molaire volumique de la solution d'éthanamine peut-on déduire de cette expérience ? 

 

Comparer avec la valeur indiquée en 2.1 $(0.5\;point)$

Le triple saut est une discipline sportive appartenant à l'athlétisme, dont le nom donne une indication sur sa pratique. 

 

Les athlètes ont une course d'élan pour gagner de la vitesse et prennent leur impulsion avant une planche (située à $13\;m$, $11\;m$ ou $9\;m$ du sable).

 

Ils enchaînent trois sauts en ne touchant le sol qu'avec un seul pied ; on a dans l'ordre un « saut à cloche-pied ou saut initial », une « foulée bondissante » et un « saut final » (figure 1)

 

 

 

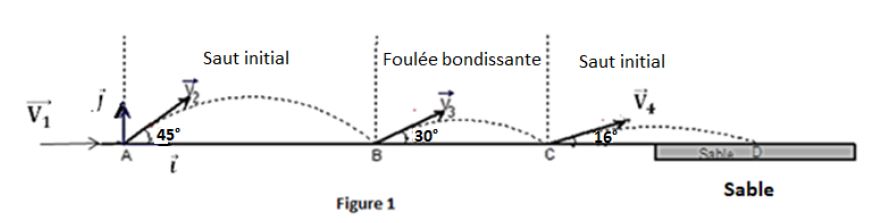
On se propose d'étudier la performance de l'athlète sénégalaise Kène NDOYE effectuant le triple saut aux Jeux Olympiques de Pékin en $2008.$

 

Pour simplifier nous assimilons l'athlète à un corps ponctuel. 

 

Le sol est horizontal. 

 

On néglige les forces de frottement.

 

3.1 La « course d'élan »

 

Dans la course d'élan l'athlète, partie sans vitesse initiale, parcourt $32\;m$ pour arriver au point $A$ de la ligne d'envol avec une vitesse horizontale $\overrightarrow{V}$ de norme $8\;m\cdot s^{-1}.$

 

Le mouvement est supposé rectiligne uniformément varié pour cette phase.

 

Évaluer l'accélération du mouvement et le temps mis par l'athlète sur ce parcours. $(0.5\;point)$

 

3.2 Le « saut initial »

 

Arrivée en $A$, l'athlète « s'envole » avec une vitesse $\overrightarrow{V}$ $\left(\text{de norme }v_{2}=9.13\;m\cdot s^{-1}\right)$ faisant un angle $\alpha=45^{\circ}$ avec l'horizontale. 

 

Dans cette phase le mouvement est rapporté à un repère $(A\;,\ \vec{i}\;,\ \vec{j})$ de plan vertical. 

 

L'origine des espaces est prise en $A$ et l'origine du temps $t=0$ au début du saut.

 

3.2.1 Établir les équations horaires du mouvement pendant cette phase. 

 

En déduire l'équation cartésienne de la trajectoire du mobile au cours du « saut initial ». $(0.75\;point)$

 

3.2.2 A l'issue du saut initial l'athlète touche le sol en $B.$ 

 

Calculer la distance $AB.$ 

 

En déduire la durée de ce saut. $(0.5\;point)$

 

3.2.3 Montrer que la valeur de la vitesse finale du « saut initial » est égale à $9.13\;m\cdot s^{-1}.$ $(0.5\;point)$

 

3.3 La « foulée bondissante »

 

On suppose que la valeur de la vitesse initiale $\overrightarrow{V}_{3}$ , de la « foulée bondissante » est égale à celle de la vitesse finale du « saut initial ». 

 

Le vecteur-vitesse $\overrightarrow{V}_{3}$ fait un angle de $30^{\circ}$ avec l'horizontale.

 

3.3.1 Quelle est la nature de la trajectoire décrite par le mobile dans la foulée bondissante ? $(0.25\;point)$

 

3.3.2 A l'issue de la « foulée bondissante » l'athlète touche le sol en un point $C$ tel que $BC=2\;m.$

 

Calculer la durée de cette phase. $(0.5\;point)$

 

3.4 Le « saut final »

 

3.4.1 L'athlète entame le « saut final » avec une vitesse $\overrightarrow{V}_{4}$ (de norme $9.13\;m\cdot s^{-1}$) faisant un angle de $16^{\circ}$ avec l'horizontale. 

 

Calculer la distance totale parcourue par Kène NDOYE à l'issue du « triple saut », distance représentant la performance de l'athlète. $(0.5\;point)$

 

3.4.2 Avec quelle vitesse aurait-elle dû s'élancer dans « le saut final » (l'angle gardant la même valeur) pour égaler le record olympique de $15.39\;m$ détenu par la camerounaise Françoise MBANGO ? $(0.5\;point)$

 

On donne : $g=9.8\;m\cdot s^{-2}$

Un groupe d'élèves, sous la supervision de leur professeur, se propose de déterminer la valeur de l'inductance $(L)$ d'une bobine et celle de la capacité $(C)$ d'un condensateur de leur laboratoire puis d'étudier les transformations et transferts d'énergie dans un circuit les associant.

 

La bobine est assimilée à un solénoïde de longueur $\ell=80\;cm$ , comportant $N=1280$ spires de surface $S=314\;cm^{2}$ chacune.

 

4.1 Détermination de l'inductance de la bobine.

 

Dans un premier temps, le groupe réalise le circuit électrique de la (figure 2) 

 

 

 

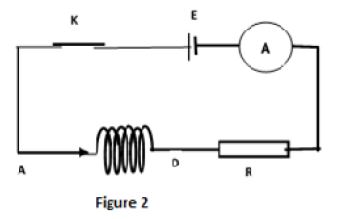
comprenant la bobine, un générateur de tension continue $(E=6V)$, un résistor de résistance $R=20\omega$ et un ampèremètre.

 

4.1.1 Donner le nom du phénomène qui se produit au niveau de la bobine lorsque l'interrupteur $K$ est fermé. $(0.25\;point)$

 

4.1.2 Reproduire le schéma de la bobine et représenter le vecteur champ magnétique $\overrightarrow{B}$ qu'elle crée en son centre. $(0.25\;point)$

 

4.1.3 A partir des expressions du flux magnétique à travers la bobine, montrer que l'inductance s'écrit :

 

$L=\mu_{0}\dfrac{N^{2}}{\ell}S.$ 

 

Calculer $L.$ $(0.5\;point)$

 

4.2 Détermination de la capacité du condensateur et considérations d'énergie.

 

Dans un second temps, le groupe réalise le montage en série de la bobine, du condensateur et du résistor (figure 3).

 

 

 

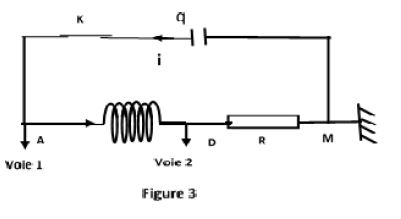
Le condensateur est initialement chargé (le circuit de charge n'est pas représenté sur la figure).

 

A la date $t=0$, l'interrupteur $K$ est fermé.

 

A l'aide d'un oscilloscope le groupe visualise l'évolution des tensions $u_{AM}$ aux bornes du condensateur et $u_{DM}$ aux bornes du résistor en fonction du temps (figure 4).

 

 

 

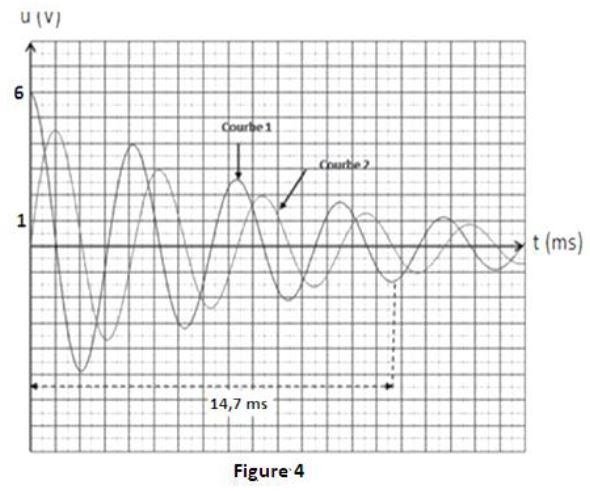
4.2.1 Attribuer à chaque courbe la grandeur associée en justifiant. 

 

Quel phénomène explique la décroissance de l'amplitude de la courbe $1$ ?

$(0.5\;point)$

 

4.2.2 Donner la relation qui lie à chaque instant l'intensité $i(t)$ et la charge $q(t)$ ainsi que celle qui lie à chaque instant l'intensité $i(t)$ et la tension $u_{DM}(t).$ 

 

Le sens arbitraire choisi pour l'orientation du circuit est sortant par rapport à l'armature du condensateur portant la charge $q.$ $(0.5\;point)$

 

4.2.3 A partir des expressions des tensions aux bornes des trois dipôles, montrer que l'équation différentielle vérifiée par $u_{AM}(t)$ s'écrit :

 

$$\dfrac{\mathrm{d}^{2}\left(u_{AM}\right)}{\mathrm{d}t^{2}}+\dfrac{R\mathrm{d}\left(u_{AM}\right)}{L\mathrm{d}t}+\dfrac{u_{AM}}{LC}=0\qquad(0.5\;point)$$

 

Déterminer graphiquement la valeur de la pseudo-période $T.$ $(0.25\;point)$

 

En déduire la valeur de la capacité $C$ du condensateur sachant que $T$ est pratiquement égale à la période propre du dipôle $(R\;L\;C).$ $(0.25\;point)$

 

4.2.4 Donner l'expression de l'énergie électromagnétique $E_{e\;,m}$ du circuit en fonction de $L$, $C$, $q$ et $i.$ 

 

En déduire son expression en fonction des tensions $u_{AM}$ et $u_{DM}$ $(0.5\;point)$

 

4.2.5 A partir de l'expression établie précédemment et en utilisant la figure $4$, calculer la valeur de $E_{e\;,m}$ à la date

$t_{2}=14.7\;ms.$ 

 

En déduire la valeur de l'énergie dissipée entre les instants $t_{0}=0\;ms$ et $t_{2}=14.7\;ms.$ $(0.5\;point)$

Le fer et le cobalt sont des métaux très utilisés dans l'industrie. 

 

Ils présentent des propriétés physiques assez voisines et sont des matériaux de base pour les aimants permanents.

 

Un laboratoire nucléaire décide de comparer d'abord la stabilité du noyau de cobalt-$59$ qui représente la quasi-totalité du cobalt naturel à celle du noyau de fer-$59$ radioisotope lourd utilisé comme traceur dans l'étude du métabolisme du fer, puis d'étudier la radioactivité du fer-$59.$

 

5.1 Étude comparative de la stabilité des noyaux de Fer-$59$ $\left(^{59}_{26}Fe\right)$ et de Cobalt-$59$ $\left(^{59}_{27}Co\right)$

 

5.1.1 Donner la composition de chaque noyau. 

 

Préciser ce que les deux noyaux ont en commun. $(0.5\;point)$

 

5.1.2 Calculer en $M_{e}V$ les énergies de liaison $E_{\ell}\left(^{59}_{26}Fe\right)$ du fer-$59$ et $E_{\ell}\left(^{59}_{27}Co\right)$ du cobalt-$59$ $(0.5\;point).$

 

L'énergie de liaison d'un noyau $^{A}_{Z}X$ de masse $m(X)$ est donnée par : 

 

$E_{\ell}=\left[Zm_{p}+(A-Z)m_{n}-m(X)\right]\cdot C^{2}$

 

5.1.3 Les valeurs des énergies de liaison permettent-elles de comparer la stabilité des deux noyaux ? 

 

Justifier puis comparer la stabilité des noyaux $^{59}_{26}Fe$ et $^{59}_{27}Co.$ $(0.5\;point)$

 

5.2 Étude de la radioactivité du noyau de fer-$59$

 

Le noyau de fer $^{59}_{26}Fe$ se désintègre spontanément en noyau de cobalt avec émission d'une particule $^{A}_{Z}X$

 

5.2.1 Écrire, en précisant les lois utilisées, l'équation de désintégration du fer-$59$ $\left(^{59}_{26}Fe\right)$. $(0.5\;point).$

 

5.2.2 Nommer la particule émise et expliquer son origine. $(0.5\;point)$

 

5.2.3 Pour déterminer l'activité initiale $A_{0}$ d'un échantillon de $\left(^{59}_{26}Fe\right)$ radioactif, le laboratoire dispose, à un instant pris comme origine du temps $(t=0)$, d'un échantillon de masse $m_{0}=1.5\;mg.$ 

 

La mesure de l'activité $A(t)$ de cet échantillon chaque intervalle de dix jours, lui a permis de constater que $\dfrac{A(t)}{A(t+10)}=1.17$ ($t$ est exprimé en jours)

 

5.2.3.1 Définir l'activité $A(t)$ d'un échantillon radioactif et l'exprimer en fonction de $A_{0}$ , de la constante radioactive $\lambda$ et de la date $t.$ $(0.5\;point)$

 

5.2.3.2 Calculer la valeur de $\lambda$ et en déduire celle de la demi-vie $T.$ $(0.5\;point)$

 

5.2.3.3 Calculer l'activité $A_{0}.$ $(0.25\;point)$

 

5.2.4 Déterminer la masse de fer désintégrée à l'instant $t=10$ jours. $(0.25\;point)$

 

Données : 

 

$1u=931.5M_{e}V/C^{2}=1.66\cdot10^{-27}kg$ ; 

 

vitesse de la lumière dans le vide : $C=3\cdot108\;m\cdot s^{-1}$

 

Masse des particules : Proton : $m_{p}=1.00728u$ ; 

 

neutron : $m_{n}=1.00867u$ ;

 

Masse des noyaux au repos : $m\left(^{59}_{26}Fe\right)=58.9348755u$ ; 

 

$m\left(^{59}_{27}Co\right)=58.9331950u$