1) Soit $t=\sqrt{45}+\sqrt{196}-\sqrt{180}-\sqrt{245}$

 

Ecris $t$ sous la forme $a\sqrt{b}+c$ où $a$, $b$ et $c$ sont des entiers; $b$ étant le plus petit entier positif possible.$\qquad 1\,pt$

2) On donne les réels $x=\dfrac{4}{7+3\sqrt{5}}\ $ et $\ y=3\sqrt{5}-7$

a) Écris $x$ avec un dénominateur rationnel.$\qquad 1\,pt$

b) Justifie que $y$ est négatif.$\qquad 1\,pt$

c) Justifie que :$x=-y\qquad 1\,pt$

d) Encadre $x$ à $10^{-2}$ près sachant que $2.236<\sqrt{5}<2.237\qquad 1\,pt$

e) On pose $z=(x-y)^{2}$

Justifie que $\sqrt{z}=-2y\qquad 1\,pt$

"`Le Sénégal vient d'administrer une belle leçon de démocratie à la face du monde par l'organisation d'élection présidentielle incontestée. Le vaincu reconnait sa défaite, félicite le vainqueur"'.

 

Une étude statistique portant sur les 30 mots de ce texte (un mot quelconque est considéré autant de fois qu'il apparait dans le texte), a donné le diagramme circulaire ci-dessous :

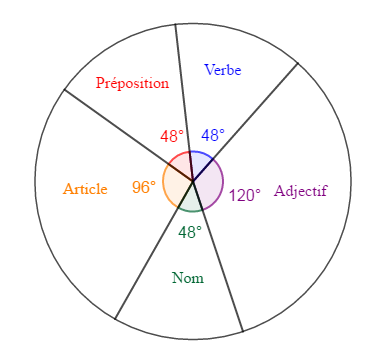
1) Lequel des caractères ci-dessous est celui qui est étudié : $\qquad 0.5\,pt$

 

$-\ $ Longueur des mots,

 

$-\ $ Nature grammaticale des mots

 

$-\ $ Le Genre grammatical des mots ?

 

2) Indique la nature de ce caractère : $\qquad 0.5\,pt$

 

3) Indique les modalités de ce caractère : $\qquad 0.5\,pt$

 

4) Dresse le tableau des effectifs de cette série : $\qquad 2\,pts$

 

5) Construis le diagramme à bandes de cette série : $\qquad 1.5\,pts$

1) Construis un triangle $MON$ rectangle en $N$ tel que $MN=7.5\;cm$ et $\widehat{MON}=30^{\circ}\ :\qquad 1\,pt$

 

2) Calcule $NO\ $ et $\ MO\ :\qquad 1\,pt$

 

3) Soit $I$ le pied de la hauteur issue de $N$, calcule $NI\ :\qquad 1\,pt$

 

4) La droite passant par $M$ et parallèle à la droite $(NI)$ coupe la droite $(ON)\ $ en $\ T.$

 

Calcule $MT\ :\qquad 1\,pt$

5) Soit $E$ le centre du cercle circonscrit au triangle $MOT$; démontre que $MET$ est un triangle équilatéral : $\qquad 1\,pt$

Dans le plan muni d'un repère orthonormal $(O\;,\ \vec{I}\;,\ \vec{J})$ on donne les points

1) Démontre que $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$ sont orthogonaux : $\qquad 1\,pt$

 

2) Calcule les coordonnées du point $E$ tel que $ABEC$ soit un parallélogramme : $\qquad 1\,pt$

 

3) Soit $F$ l'image de $B$ par la translation de vecteur $\overrightarrow{CE}.$

 

Calcule les coordonnées de $F\ :\qquad 1\,pt$

 

4) Justifie que $B$ est le milieu de $\left[AF\right]$

 

 

 

$\begin{array}{c}\blacktriangleright\ \boxed{\text{Correction BFEM 2012}}\end{array}$