BFEM Mathématiques 2015
Exercice 1 (6 points)
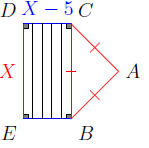
La figure codée ci-contre est une représentation d'un terrain formé de deux parcelles, l'une triangulaire et l'autre rectangulaire de longueur $x$ et de largeur $X-5$ ; l'unité de longueur est le mètre.
1) Détermine les valeurs de $X$ pour lesquelles le périmètre de la parcelle $ABC$ est strictement plus grand que celui de la parcelle $BCDE.$ (1.5 pts)
2) a) montre Que l'aire de la parcelle $ABC$ est $\dfrac{X^{2}\sqrt{3}}{4}m^{2}$ (1.5 pts)
b) Détermine $X$ pour que l'aire de la parcelle $BCDE$ soit égale à $\dfrac{ 3X^{2}}{4} m^{2}$ (1.5 pts)
3) On suppose que ce terrain représenté par le polygone $ABEDC$ est cloturé avec un grillage qui a couté $90\,000\;F$
Sachant qu'on a laissé une entrée de $2\;m$ et que le grillage utilisé est acheté à $1\,500\;F$ le mètre, calcule $X.$ (1.5 pts)
Exercice 2 (6 points)
Le tableau statistique ci-dessous donne la répartition des usagers transportés en une journée par une entreprise de transport selon le prix du ticket de section achetée.
$$\begin{array}{|c|c|c|c|c|c|c|} \hline\text{Prix du ticket de section en F CFA}&100&150&200&250&300&350\\ \hline\text{Nombre de tickets}&2\,480&1\,060&820&960&780&1\,100\\ \hline\text{Effectifs cumulés croissants}&2\,480&3\,580&4\,320&5\,320&6\,100&7\,200\\ \hline\text{Effectifs cumulés décroissants}&7\,200&4\,720&3\,660&2\,840&1\,880&1\,100\\ \hline \end{array}$$
1) Quel est le caractère statistique étudié ? (0.5 pt)
2) Combien cette entreprise a-t-elle transporté d'usagers ce jour ? (0.5 pt)
3) Donne les modalités du caractère étudié. (0.5 pt)
4) Quel est le nombre d'usagers ayant acheté un ticket valant moins de $250\;F\ ?$ (0.5 pt)
5) Quel est le nombre d'usagers a) ayant acheté un ticket valant au moins $250\;F\ ?$ (0.5 pt)
6) Quel est le prix médian du ticket de section de ce jour (médiane de cette série) ? (1 pt)
7) Calcule le prix moyen du ticket de section de ce jour (la moyenne de cette série). (1 pt)
8) Construis le diagramme circulaire de la série (0.5 pt)
Exercice 3 (8 points)
Le plan est muni d'un repère orthonormal $(0\;,\ I\;,\ J).$
1) Donne la relation, entre les coordonnées traduisant l'appartenance du point $A\begin{pmatrix} m\\n\end{pmatrix}$ à la droite $(D)\ :\ ax+by+c=0.$ (0.5 pt)
2) Donne la relation, entre les coordonnées, traduisant la colinéarité des vecteur $\vec{u}\begin{pmatrix} x\\y\end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} a\\b\end{pmatrix}.$ (0.5 pt)
3) Donne la relation, entre les coefficients directeurs, traduisant la perpendicularité des droites $(D_{1})\ :\ y=ax+b\ $ et $\ (L)\ :\ y=px+q.$ (0.5 pt)
4) On donne le point $A'\begin{pmatrix} 2\\3\end{pmatrix}$ le vecteur $\vec{u}\begin{pmatrix} 1\\2\end{pmatrix}$ et la droite $(D')$ passant par $A'$ et de vecteur directeur $\vec{u}.$
a) Détermine une équation cartésienne de la droite $(D').$ (1 pt)
b) Justie que le point $B\begin{pmatrix} 4\\1\end{pmatrix}$ appartient à la droite $(D').$ (0.5 pt)
c) Montre que l'équation réduite de la droite $(L')$ perpendiculaire à la droite $(D')$ au point $E$, milieu de $[A'B]$, est $y=\dfrac{1}{2}x-\dfrac{1}{2}.$ (0.5 pt)
d) justie que $IA'=IB.$ (1.5 pt)
e) Montre que la mesure de l'aire de la surface du triangle $A'BI$ est $5.$ (1.5 pt)
f) Fais une figure complète pour la question 4. (1.5 pt)

Commentaires
Bintou sow (non vérifié)
ven, 05/21/2021 - 15:11
Permalien
J'aime bien
Ajouter un commentaire