Exercice 1  (5 points)

On donne trois réels $a$, $b$ et $c$ tels que: $a=7-5\sqrt{2}\, b\,=\,-7-5\sqrt{2}\ $ et $\ c\,=\,-7+5\sqrt{2}$

1) Démontre que le réel $a$ est l'inverse du réel $b$.          (1 point)

2) Justifie que a et c sont opposé.       (1 point)

3) Démontre que $\dfrac{b}{a}-\dfrac{c}{b}=b^2+c^2$.        (1 point)

4) Calcule $a^2$ puis déduis-en une écriture simplifiée du réel $w=\sqrt{99-70\sqrt{2}}$       (2 points)

Exercice 2  (5 points)

Les notes des $160$ candidats à un concours sont consignées dans le tableau suivant:
$$\begin{array}{|c|c|c|c|c|c|} \hline\text{Notes}&[10\;;\ 12[&[12\;;\ 14[&[14\;;\ 16[&[16\;;\ 18[&[18\;;\ 20[\\\hline\text{Fréquences}&0.3&x&0.2&0.15&y\\\hline \end{array}$$
1) Donne une interprétation de la valeur $0,3$ fréquence de la classe $[10 ; 12[$.          (0.5 point)

2) Calcule $x$ et $y$ sachant que $25\%$ des élèves ont une note supérieure ou égale à $16$.      (1.5 point)

3) On donne $x = 0,25$ et $y = 0,1$.

a) Calcule la moyenne des notes.      (1.5 point)

b) Construis le diagramme des fréquences cumulées décroissantes.      (1.5 point)

Exercice 3   (5 points)

$ABC$ est triangle isocèle en $A$.
La hauteur issue de A coupe le segment $[BC]$ en $H$. On donne $BC \ =\ 6 \ cm$ et $AH\ =\ 4\ cm$.
Soit $M$ un point du segment $(BH]$ tel que $BM = x$. La parallèle à la droite $(AH)$ et passant
par $M$ coupe la droite $(AB)$ en $P$ et la droite $(AC)$ en $Q$.

1) Fais la figure et calcule $BH$.               (0,5+0,5 point)

2) Montre que $\dfrac{MP}{AH}=\dfrac{x}{3}$ puis en déduire $MP$ en fonction de $x$.       1 point

3) Exprime $MC$ en fonction de $x$ .          (0.5 point)

4) Montre que $MQ=\dfrac{4}{3}(6-x)$.         (1 point)

5) Pour quelles valeur de $x$ a-t-on $MQ = 3MP$ ?              (0.5 point)

6) Quelle serait alors la position du point $P$ sur le segment $[AB]$?         (1 point)

Exercice 4   (5 points)

On considère la figure codée ci-dessous :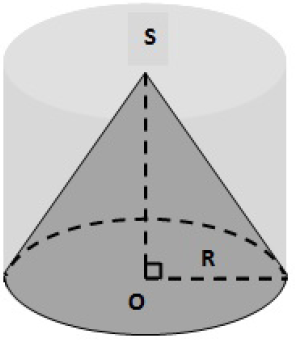

On donne les formules de calcul de volume de solides ci-dessous :

volume d'un ône de révolution : $V_{CONE}=\dfrac{1}{3}\times\pi\times R^2\times h$  
 
Volume d'une boule: $V_{BOULE}=\dfrac{4}{3}\times\pi\times R^3$.

Volume d'un cylindre: $V_{CYLINDRE}= \pi\times R^2\times h$   .

$R$ désigne le rayon et $h$ la hauteur.

1) Calcule le volume exact de chacun de ces trois solides pour $h \ =\ R =\ 1\ m$.        (1.5 point)

2) Exprime le volume d'une boule et c lui d'un cylindre en fonction du volume d un ône de révolution pour $R\ =\ h$.      (2 points)

3) Un récipient servant à recueillir de l'eau de pluie est constitué d'un cylindre de rayon $R\ =\ 50\ cm$ ouvert à sa base supérieure et d'un ône de révolution situé à l'intérieur de ce cylindre. Le ône et le cylindre ont la même hauteur et la base du ône coïncide avec la base inférieure fermée du cylindre (voir figure ci-contre). Exprime le volume de ce récipient en fonction du volume cylindre.

Correction BFEM 2017