Série d'exercices sur l'orthogonalité et le produit scalaire dans le plan 1e S
Exercice 1
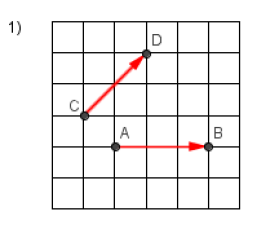
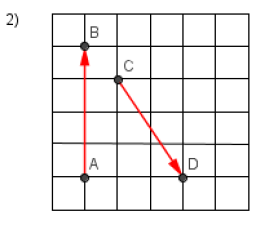
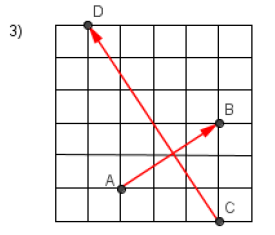
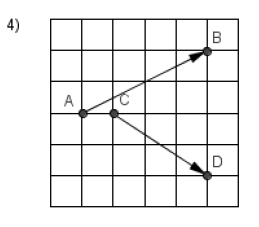
Calculer le produit scalaire
$\overrightarrow{AB}\cdot\overrightarrow{CD}$ dans les figures ci-dessous :
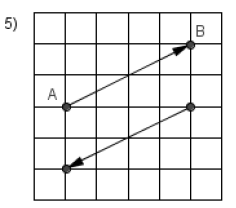
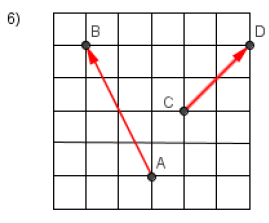
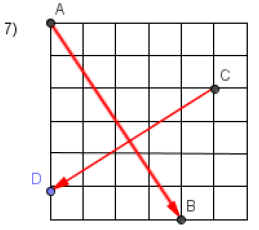
Exercice 2
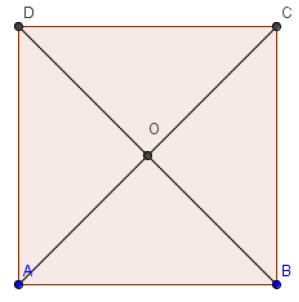
Soit $ABCD$ un carré de centre $O$ tel que $AB=4.$
Calculer les produits scalaires :
$\overrightarrow{AB}\cdot\overrightarrow{BC}\;,\quad\overrightarrow{AB}\cdot\overrightarrow{CD}\;,\quad\overrightarrow{AB}\cdot\overrightarrow{AC}\;,\quad\overrightarrow{CD}\cdot\overrightarrow{OA}\;,\quad\overrightarrow{OA}\cdot\overrightarrow{AC}$
$\overrightarrow{DB}\cdot\overrightarrow{BC}\;,\quad\text{et}\quad\overrightarrow{AB}\cdot\overrightarrow{DO}$
Exercice 3
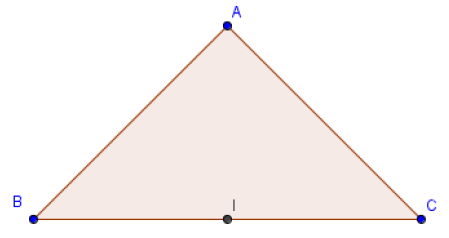
$ABC$ est un triangle isocèle de sommet $A\;,\ BC=4.$
Le point $I$ est le milieu de $[BC]$.
Calculer
$\overrightarrow{IB}\cdot\overrightarrow{IC}\;,\quad\overrightarrow{BI}\cdot\overrightarrow{BC}\;,\quad\overrightarrow{AI}\cdot\overrightarrow{BC}\;,\quad\overrightarrow{BA}\cdot\overrightarrow{BC}\;,\quad\overrightarrow{AC}\cdot\overrightarrow{CI}$
Exercice 4
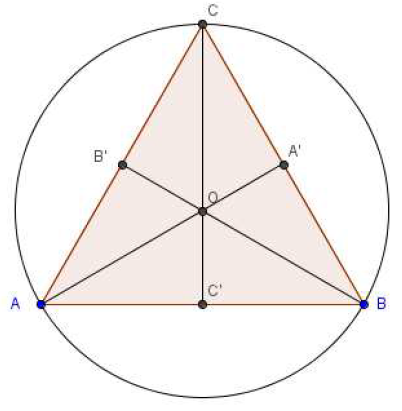
Soit $ABC$ un triangle équilatéral de coté 6, $O$ le centre de son cercle circonscrit, $A'\;,\ B'\;,\ C'$ les milieux respectifs de $[BC]\;,\ [CA]\;,\ [AB]$.
Calculer les produits scalaires :
$\overrightarrow{AB}\cdot\overrightarrow{AC}\;,\quad\overrightarrow{OB}\cdot\overrightarrow{OC}\;,\quad\overrightarrow{OA}\cdot\overrightarrow{BC}\;,\quad\overrightarrow{OB}\cdot\overrightarrow{AA'}\quad\text{et}\quad\overrightarrow{BC'}\cdot\overrightarrow{CB'}$
Exercice 5
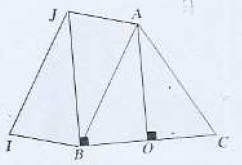
Dans la figure ci-dessous, $ABC$ est un triangle isocèle de sommet $A\text{ et }ABIJ$ est un parallélogramme.
On pose $BC=a$.
Exprimer le produit scalaire $\overrightarrow{BC}\cdot\vec{v}$ en fonction de $a$ dans chacun des cas suivants :
$1)\ \vec{v}=\overrightarrow{AB}\qquad 2)\ \vec{v}=\overrightarrow{JC}\qquad 3)\ \vec{v}=\overrightarrow{AI}\qquad 4)\ \vec{v}=\overrightarrow{CI}$
$5)\ \vec{v}=\overrightarrow{BA}+\overrightarrow{OJ}\qquad 6)\ \vec{v}=2\overrightarrow{OI}\qquad 7)\ \vec{v}=\overrightarrow{IA}-\overrightarrow{AJ}\qquad 8)\ \vec{v}=\overrightarrow{CI}+\overrightarrow{OJ}$
Exercice 6
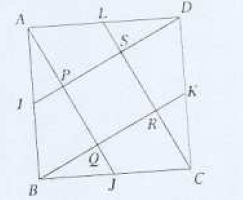
$ABCD$ est un carré.
$I\;,\ J\;,\ K\;,,\ L$ sont les milieux respectifs des cotés $[AB\;,\ [BC]\;,\ [CD]\text{ et }[DA]$ du carré.
Les droites $(AJ)\text{ et }(DI)$ se coupent en $P$, les droites $(AJ)\text{ et }(KB)$ se coupent en $Q$,
les droites $(CL)\text{ et }(DI)$ se coupent en $S$, les droites $(CL)\text{ et }(KB)$ se coupent en $R$.
1) a) Exprimer $\overrightarrow{AJ}$ en fonction de $\overrightarrow{AB}\text{ et }\overrightarrow{AC}$, puis $\overrightarrow{DI}$ en fonction de $\overrightarrow{DA}\text{ et }\overrightarrow{DB}$
b) En déduire que : $\overrightarrow{AJ}\cdot\overrightarrow{DI}=0$
2) a) Établir que $\overrightarrow{PS}\cdot\overrightarrow{ID}=\overrightarrow{AL}\cdot\overrightarrow{AD}$
b) En déduire l'expression de $PS$ en fonction du coté $a$ du carré $ABCD$.
c) Montrer que le quadrilatère $PQRS$ est un carré et exprimer son aire en fonction de celle du carré $ABCD$
Démontrer que quels que soient les vecteurs
$\vec{u}\;,\ \vec{v}\text{ et }\vec{w}\ :$
$$||\vec{u}||^{2}+||\vec{v}||^{2}+||\vec{w}||^{2}=\dfrac{1}{4}\left(||\vec{u}+\vec{v}+\vec{w}||^{2}+||\vec{u}+\vec{v}-\vec{w}||^{2}+||\vec{u}-\vec{v}+\vec{w}||^{2}+||-\vec{u}+\vec{v}+\vec{w}||^{2}\right)$$
Exercice 8
Démontrer que quels que soient les vecteurs $\vec{u}\text{ et }\vec{v}$ : les vecteurs $\vec{u}+\vec{v}\text{ et }\vec{u}-\vec{v}$ sont orthogonaux si et seulement si $\vec{u}\text{ et }\vec{v}$ ont la même norme.
Application :
Soit un parallélogramme $ABCD$.
Démontrer que les diagonales $[AC]\text{ et }[BD]$ sont orthogonales si et seulement si $AC=BD.$
Indication :
On pourra poser $\overrightarrow{AB}=\vec{u}\text{ et }\overrightarrow{AB}=\vec{v}$
Exercice 9
Soit $ABCD$ un quadrilatère.
Démontrer que l'on a :
$$\overrightarrow{AB}^{2}+\overrightarrow{CD}^{2}-\overrightarrow{BC}^{2}-\overrightarrow{AD}^{2}+2\overrightarrow{AC}\cdot\overrightarrow{BD}=0$$
En déduire une condition nécessaire et suffisante pour que les diagonales $(AC)\text{ et }(BD)$ soient perpendiculaires.
Exercice 10
Démontrer que quels que soient les points $A\;,\ B\;,\ C\;,\ D\ :$
$$\overrightarrow{DA}\cdot\overrightarrow{BC}+\overrightarrow{DB}\cdot\overrightarrow{CA}+\overrightarrow{DC}\cdot\overrightarrow{AB}=0$$
Déduire de cette relation que les trois hauteurs d'un triangle sont concourantes.
Exercice 11
1) Montrer que dans un triangle $ABC$ d'orthocentre $H$, on a :
$$\overrightarrow{HA}\cdot\overrightarrow{HB}=\overrightarrow{HB}\cdot\overrightarrow{HC}=\overrightarrow{HC}\cdot\overrightarrow{HA}$$
2) Réciproquement, soit $M$ un point tel que :
$$\overrightarrow{MA}\cdot\overrightarrow{MB}=\overrightarrow{MB}\cdot\overrightarrow{MC}=\overrightarrow{MC}\cdot\overrightarrow{MA}$$
Calculer les produits scalaires
$$\overrightarrow{MA}\cdot\overrightarrow{CB}\;,\ \overrightarrow{MB}\cdot\overrightarrow{CA}\text{ et }\overrightarrow{MC}\cdot\overrightarrow{AB}$$
En déduire que $M=H.$
Exercice 12
Soit $ABC$ un triangle, $H$ l'orthocentre, $A'\;,\ B'\;,\ C'$ les projetés orthogonaux respectifs de $A\;,\ B\;,\ C$ sur le coté opposé.
1) Utiliser $\overrightarrow{BH}\cdot\overrightarrow{AC}=0$ pour démontrer que : $$\overline{A'A}\cdot\overline{A'H}=-\overline{A'B}\cdot\overline{A'C}$$
2) Comparer les produits scalaires $\overrightarrow{AH}\cdot\overrightarrow{AB}\text{ et }\overrightarrow{AH}\cdot\overrightarrow{AC}$
Démontrer que $$\overline{AH}\cdot\overline{AA'}=\overline{AB}\cdot\overrightarrow{AC'}=\overline{AC}\cdot\overline{AB'}$$
3) Démontrer de même que : $$\overline{HA}\cdot\overline{HA'}=\overline{HB}\cdot\overline{HB'}=\overline{HC}\cdot\overline{HC'}$$
Exercice 13
Démontrer que si $ABC\text{ et }A'B'C'$ sont deux triangles tels que :
la droite $d_{1}$ contenant $A$ et orthogonale à $(B'C')$
la droite $d_{2}$ contenant $B$ et orthogonale à $(C'A')$
la droite $d_{3}$ contenant $C$ et orthogonale à $(A'B')$ sont concourantes, alors
la droite $d'_{1}$ contenant $A'$ et orthogonale à $(BC)$
la droite $d'_{2}$ contenant $B'$ et orthogonale à $(CA)$
la droite $d'_{3}$ contenant $C'$ et orthogonale à $(AB)$ sont concourantes.
Indications :
1) Établir d'abord que $\overrightarrow{AC}\cdot\overline{B'C'}=\overrightarrow{BC}\cdot\overline{A'C'}$ en utilisant le point de concours de $d_{1}\;,\ d_{2}\;,\ d_{3}$.
2 Justifier l'existence d'un point $\Omega$ tel que : $$\overline{\Omega'A}\cdot\overline{B'C'}=\overline{\Omega'B}\cdot\overline{C'A'}=0$$
3) Démontrer alors que $\overline{\Omega'C}\cdot\overline{A'B'}=0$ et conclure.
Exercice 14
Le triangle $OAB$ est rectangle en $O$.
Une droite $\Delta$ passant par $A$ coupe la hauteur $(OH)\text{ en }M$ et le cercle de diamètre $[AB]\text{ en }N$.
Montrer que $$\overrightarrow{AM}\cdot\overrightarrow{AN}=AO^{2}$$
Exercice 15
Soit $\Gamma$ le cercle de centre $O$ circonscrit à un triangle $ABC$.
La hauteur issue de $A$ coupe $(BC)\text{ en }A'\text{ et }\Gamma\text{ en }D.$
Soit $E$ le point diamétralement opposé à $A$ sur $\Gamma$. Montrer que :
$$\overrightarrow{AB}\cdot\overrightarrow{AD}=\overrightarrow{AC}\cdot\overrightarrow{AD}=\overrightarrow{AE}\cdot\overrightarrow{AA'}$$
Exercice 16
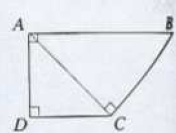
Dans le trapèze rectangle $ABCD$, la diagonale $[AC]$ est orthogonale au coté $[BC]$.
En calculant de deux façons le produit scalaire $\overrightarrow{AB}\cdot\overrightarrow{AC}$,
montrer que $AC^{2}=AB\times CD$
Exercice 17
Soit $ABC$ un triangle équilatéral de coté $m$.
1) $I$ est le barycentre de $(B\;,\ 4)\text{ et }(A\;,\ 1)\text{ et }J$ le barycentre de $(C\;,\ 2)\text{ et }(A\;,\ 3).$
a) Calculer le produit scalaire $\overrightarrow{AI}\cdot\overrightarrow{AC}$ en fonction de $m$
b) Prouver que la droite $(IJ)$ est orthogonale à la droite $(AC).$
2) Soit $a\;,\ b\;,\ c$ trois réels.
On désigne par $K$ le barycentre de $(A\;,\ a)\text{ et }(B\;,\ b)$ et par $L$ celui de $(A\;,\ a+b-c)\text{ et }(C\;,\ c)$
Montrer que les droites $(KL)\text{ et }(AC)$ sont orthogonales si et seulement si $b=2c.$
Exercice 18
Soit $ABCD$ un carré, $I\text{ et }J$ les milieux de $[AB]\text{ et }[AD]$.
Montrer que la médiane issue de $A$ du triangle $AID$ est une hauteur de triangle $ABJ$
Exercice 19
Sur un cercle de centre $\Omega$ et de rayon $r$, on place quatre points $A\;,\ B\;,\ A'\text{ et }B'$ tels que les droites $(BB')\text{ et }(AA')$ soient orthogonales et sécantes en $O.$
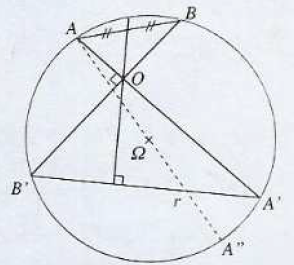
1) En utilisant le diamètre $[AA'']$, montrer que : $$\overrightarrow{OA}\cdot\overrightarrow{OA'}=O\Omega^{2}-A\Omega^{2}$$
2) Montrer que la médiane issue de $O$ du triangle $OAB$ est une hauteur de triangle $OA'B'.$
(On pourra prouver que ($\overrightarrow{OA}+\overrightarrow{OB})\cdot\overrightarrow{A'B'}=0)$
Exercice 20
A l'extérieur d'un triangle $ABC$, on construit deux carrés.
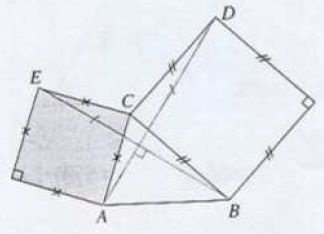
1) Montrer que $\overrightarrow{CA}\cdot\overrightarrow{CB}=-\overrightarrow{CD}\cdot\overrightarrow{CE}$
2) Montrer que les droites $(AD)\text{ et }(EB)$ sont orthogonales et que $AD=EB.$
Exercice 21
A partir d'un triangle équilatéral $ABE$ de coté 2, on construit deux carrés.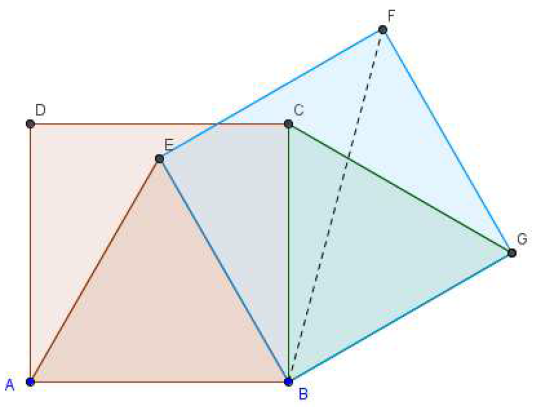
1) a) Calculer les produits scalaires $\overrightarrow{BC}\cdot\overrightarrow{BE}\text{ et }\overrightarrow{EA}\cdot\overrightarrow{EB}$
b) Montrer que le triangle $BCG$ est équilatéral.
En déduire $\overrightarrow{BC}\cdot\overrightarrow{BG}$ puis $\overrightarrow{DA}\cdot\overrightarrow{EF}$
c) Calculer $\overrightarrow{AE}\cdot\overrightarrow{EF}$
d) Calculer $\overrightarrow{DE}\cdot\overrightarrow{BF}$
En déduire que les points $D\;,\ E\;,\ G$ sont alignés.
2) En utilisant le repère $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AD})$,
calculer $\overrightarrow{DE}\cdot\overrightarrow{BF}$
Conclure
Exercice 23
Soit $ABCD$ un carré de coté 6.
$I$ le barycentre de $(A\;,\ 2)\text{ et }(B\;,\ 1)$, $J$ celui de $(A\;,\ 1)\text{ et }(D\;,\ 2)$, et $K$ le point d'intersection des droites $(ID)\text{ et }(JC)$.
1) Faire une figure.
Montrer que les droites $(ID)\text{ et }(JC)$ sont perpendiculaires.
2) En utilisant un produit scalaire, montrer que : $DK\times DI=\dfrac{1}{2}DA^{2}$
3) Calculer les distances $KD\text{ et }KI.$
4) a) Soit $L$ le projeté orthogonal de $A$ sur la droite $(DI)$.
A l'aide d'un produit scalaire, calculer $IL,\text{ puis }LK$
b) En déduire la construction d'un carré de coté $\dfrac{6}{5}\sqrt{10}$
Exercice 24
Soit un triangle $ABC$ rectangle en $A$ tel que $AC=2\;AB.$
on désigne par $A'$ le milieu de $[BC]$ et par $H$ le projeté orthogonal de $A$ sur la droite $(BC)$.
Le point $H$ se projette orthogonalement en $I$ sur $(AB)$ et en $J$ sur $(AC).$
Le but de l'exercice est de montrer que les droites $(AA')\text{ et }(IJ)$ sont orthogonales.
1) Calcul vectoriel
Établir que $\overrightarrow{AA'}\cdot\overrightarrow{IJ}=0$
Conclure.
2) Calcul analytique
a) On pose $\vec{i}=\overrightarrow{AB}\text{ et }\vec{j}=\dfrac{1}{2}\overrightarrow{AC}$
Justifier que $(A\;,\ \vec{i}\;,\ \vec{j})$ est un repère orthonormal du plan.
b) Déterminer les coordonnées des points $A\;,\ B\;,\ C\text{ et }D$ dans ce repère.
c) Déterminer une équation de la hauteur issue de $A$ à l'aide d'un vecteur normal.
Déterminer les coordonnées du point $H$, puis les coordonnées des points $I\text{ et }J$.
d) Calculer $\overrightarrow{AA'}\cdot\overrightarrow{IJ}$
Conclure.
Exercice 25
Relations métriques dans un triangle rectangle
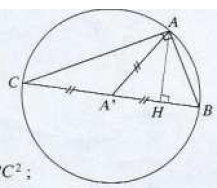
On se propose de démontrer que les six phrases suivantes sont équivalentes :
$(1)\ ABC\text{ est rectangle en }A.\quad(2)\ AB^{2}+AC^{2}=BC^{2}$
$(3)\ AA'=\dfrac{1}{2}BC\qquad (4)\ AB^{2}=\overline{BH}\times \overline{BC}$
$(5)\ AH^{2}=-\overline{HB}\times\overline{HC}\qquad(6)\ AB\times AC=AH\times BC.$
A) 1) En utilisant deux écritures de $\overrightarrow{BA}\cdot\overrightarrow{BC}$,
justifier que les propriétés $AB^{2}=\overline{BH}\times\overline{BC}$ et $ABC$ est rectangle en $A$ sont équivalentes.
2) Démontrer qu'il est équivalent d'écrire :
$$\overrightarrow{AB}\cdot\overrightarrow{AC}=0\text{ et }AH^{2}=-\overline{HB}\times\overline{HC}$$
3) En donnant deux écritures de l'aire d'un triangle $ABC$, montrer que (6) et (1) sont équivalentes.
4) Déduire des égalités (2) et (6) que, si $ABC$ est un triangle rectangle en $A$ de hauteur $[AH)$, alors on a l'égalité : $$\dfrac{1}{AH^{2}}=\dfrac{1}{AB^{2}}+\dfrac{1}{AC^{2}}$$
B) $ABC$ est un triangle rectangle en $A.$
Calculer $BH\;,\ AH\text{ et }AA'$.
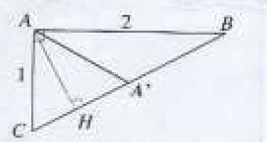
C) L'aire du triangle $ABC$ étant égale à 80 unités d'aires, ce triangle est-il rectangle ?
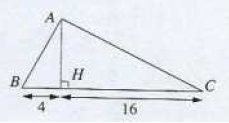
D) On donne deux segments de longueurs $a\text{ et }b$.
Construire à la règle et au compas un segment de longueur $\sqrt{ab}$.
(Penser à utiliser une des relations métriques dans un triangle rectangle)
Lignes de niveau
Exercice 26
Soient $A\;,\ B$ deux points distincts tels que $AB=2a$.
Déterminer l'ensemble des points $M$ vérifiant :
$1)\ MA^{2}-MB^{2}=a^{2}\qquad 2)\ MA^{2}+MB^{2}=3a^{2}$
$3)\ MA=3MB\qquad 4)\ \overrightarrow{AB}\cdot\overrightarrow{AM}=-2a^{2}$
$5)\ \overrightarrow{MA}\cdot\overrightarrow{MB}=-\dfrac{3a^{2}}{4}\qquad 6)\ MA^{2}+3MB^{2}=4a^{2}$
$7)\ MA^{2}-4MB^{2}=4a^{2}$
Exercice 27
Soient les points $A\;,\ B\;,\ C\text{ et }\alpha\;,\ \beta\;,\ \gamma$ des réels dont la somme n'est pas nulle.
Soit $G$ le barycentre du système $\{(A\;,\ \alpha)\;;\ (B\;,\ \beta)\;;\ (C\;,\ \gamma)\}.$
1) Démontrer que, pour tout point $M$ du plan :
$\alpha MA^{2}+\beta MB^{2}+\gamma MC^{2}=(\alpha+\beta+\gamma)MG^{2}+\alpha GA^{2}+\beta GB^{2}+\gamma GC^{2}$
2) Les points $A\;,\ B\;,\ C$ et les réels $\alpha\;,\ \beta\;,\ \gamma$ étant fixés, déterminer l'ensemble des points $M$ du plan tels que :
$\alpha MA^{2}+\beta MB^{2}+\gamma MC^{2}=k$, $k$ réel fixé.
3) Application :
Soit $ABC$ un triangle rectangle en $A$ tel que $BC=2a\text{ et }I$ le milieu de $[BC].$
a) Démontrer que $G$, défini par $4 \overrightarrow{GA}-\overrightarrow{GB}-\overrightarrow{GC}=\vec{0}$ est le symétrique de $I$ par rapport à $A$.
b) Déterminer $\mathcal{E}$, ensemble des points $M$ du plan tels que :
$4MA^{2}-MB^{2}-MC^{2}=-4a^{2}$ (on notera que $A\in\;\mathcal{E}$)
4) Application :
Soit $a$ réel positif fixé et $A\;,\ B\;,\ C$ points du plan tels que
$BC=2a\;,\ CA=3a\;,\ AB=3a$.
a) Déterminer $G$ barycentre de $\{(A\;,\ -2)\;;\ (B\;,\ 3)\;;\ (C\;,\ 3)\}$.
b) Déterminer l'ensemble des points $M$ du plan tels que : $$-2MA^{2}+3MB^{2}+3MC^{2}=54a^{2}$$
Exercice 28
Soient les points $A\;,\ B\;,\ C\text{ et }\alpha\;,\ \beta\;,\ \gamma$ des réels dont la somme est nulle.
1) Démontrer que, pour tout point $M$ du plan :
$a)\ \alpha \overrightarrow{MA}+\beta \overrightarrow{MB}+\gamma \overrightarrow{MC}\text{ est un vecteur fixe }\vec{V}$
$b)\ \alpha MA^{2}+\beta MB^{2}+\gamma MC^{2}=2\overrightarrow{MA}\cdot\vec{V}+\beta AB^{2}+\gamma AC^{2}$
2) Les points $A\;,\ B\;,\ C$ et les réels $\alpha\;,\ \beta\;,\ \gamma$ étant fixés $(\alpha+\beta+\gamma=0)$,
déterminer l'ensemble des points $M$ du plan tels que : $\alpha MA^{2}+\beta MB^{2}+\gamma MC^{2}=k$, $k$ réel fixé.
3) Application :
Soit $A\;,\ B\;,\ C$ points du plan tels que $BC=5a\;,\ CA=3a\;,\ AB=4a$.
($a$ réel positif fixé).
Déterminer l'ensemble des points $M$ du plan tels que : $$MA^{2}+2MB^{2}+MC^{2}=5a^{2}$$
Construire cet ensemble.
4) Application :
Soit $ABC$ un triangle équilatéral.
Déterminer l'ensemble des points $M$ du plan tels que : $$-2MA^{2}+MB^{2}+MC^{2}=0$$
Exercice 29
Soit $ABC$ un triangle de centre de gravité $G$.
1) Établir que : $$GA^{2}+GB^{2}=\dfrac{1}{2}GA^{2}+\dfrac{BC^{2}}{2}$$
(on pourra utiliser le théorème de la médiane)
2) En déduire que : $$GA^{2}+GB^{2}+ GC^{2}=\dfrac{1}{3}(AB^{2}+BC^{2}+CA^{2})$$
3) Quel est l'ensemble des points $M$ du plan tels que : $MA^{2}+MB^{2}+MC^{2}=BC^{2}+CA^{2}+AB^{2}$ ?
Exercice 30
On donne un triangle $ABC.$
Déterminer l'ensemble des points $M$, tels que :
$1)\ (2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC})\cdot\overrightarrow{AM}=(\overrightarrow{MA}-2\overrightarrow{MB}+3\overrightarrow{MC})\cdot\overrightarrow{BC}$
$2)\ (3\overrightarrow{MA}+\overrightarrow{MB}-4\overrightarrow{MC})\cdot\overrightarrow{AM}=(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC})\cdot\overrightarrow{AB}$
$3)\ (\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC})\cdot(\overrightarrow{AB}+\overrightarrow{AC})=0$
$4)\ (2\overrightarrow{MA}-3\overrightarrow{MB}+4\overrightarrow{MC})\cdot(\overrightarrow{MA}-3\overrightarrow{MB}+2\overrightarrow{MC})=0$
Exercice 31
On donne un rectangle $ABCD$ tel que $AB=a\text{ et }AD=b$ et l'on considère l'application $f\text{ de }\mathcal{P}\text{ dans }\mathbb{R}$, définie par : $f\ :\ M\mapsto MA^{2}+MB^{2}+MC^{2}+MD^{2}$.
1) Pour tout point $M$, démontrer que :
$f(M)= 4OM^{2}+h$, où $O$ est le centre du rectangle et $h$ un réel que l'on exprimera en fonction de $a\text{ et }b.$
2) En déduire les lignes de niveau de l'application $f$.
Comment choisir le réel $k$ pour que la ligne de niveau $k$ soit le cercle circonscrit au triangle ?
Exercice 32
Soit $ABC$ un triangle rectangle en $A$, de centre de gravité $G$, et $A'$ le milieu du segment $[BC]$
On pose $BC=a.$
1) Exprimer $4\overrightarrow{GA}\cdot\overrightarrow{AA'}$ en fonction de $a.$
2) Exprimer $GB^{2}+GC^{2}$ en fonction de $a$.
En déduire que $GA^{2}+ GB^{2}+ GC^{2}=\dfrac{2}{3}a^{2}$
3) Prouver que, pour tout point $M$ du plan, on a : $$MA^{2}+MB^{2}+MC^{2}=GA^{2}+GB^{2}+GC^{2}+3MG^{2}$$
4) Déterminer et représenter l'ensemble des points $M$ du plan tels que :
$$MA^{2}+MB^{2}+MC^{2}=\dfrac{3}{4}a^{2}$$
Exercice 33
Soit $ABC$ un triangle isocèle tel que: $AB=AC=5\text{ et }BC=6$.
1) Montrer que $\overrightarrow{AB}\cdot\overrightarrow{AC}=7$
2) Soit $G$ le barycentre de $\{(A\;,\ 2)(B\;,\ 3)(C\;,\ 3)\}.$
Construire $G$ et montrer que $AG = 3$.
3) Soit $f$ l'application qui, à tout point $M$ du plan, associe :
$$f(M)=2\overrightarrow{MB}\cdot\overrightarrow{MC}+\overrightarrow{MC}\cdot\overrightarrow{MA}+\overrightarrow{MA}\cdot\overrightarrow{MB}$$
Montrer que $f(M)=f(G)+4MG^{2}$.
4) Calculer $f(A)\text{ et }f(G)$.
5) Déterminer l'ensemble des points $M$ tels que $f(M)=f(A)$ et représenter cet ensemble.
Exercice 34
Construire un triangle $ABC$ tel que : $AB=8\;,\ AC=5\text{ et }BC=6$.
$I$ est le milieu de $[AB].$
1) Construire l'ensemble $\mathcal{E}$ des points $M$ tels que : $MA^{2}+MB^{2}=82.$
2) Choisir $k$ pour que la ligne de niveau $\mathcal{L}_{k}$ de la fonction $f\ :\ M\mapsto MA^{2}+MB^{2}$ passe par $C.$
3) Construire l'ensemble $\mathcal{F}$ des points $M$ tels que : $$61\leq MA^{2}+MB^{2}\leq 82$$
4) On note $\mathcal{G}_{k}$ l'ensemble des points $M$ tels que :
$MA^{2}+ MB^{2}-2MC^{2}=k$, où $k$ est un réel donné.
a) Quelle est la nature de $\mathcal{G}_{k}$ ?
b) Choisir $k$ pour que $\mathcal{G}_{k}$ passe par $B$, et construire $\mathcal{G}_{k}$ dans ce cas particulier.
Équations de cercles
Exercice 35
Le plan est rapporté à un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j})$
Soit $\mathcal{E}$ l'ensemble des points $M(x\;,\ y)$ du plan défini par :
$x^{2}+y^{2}-2 mx-4 my+6 m^{2}-4=0\;,\text{ avec }m\in\;\mathbb{R}..$
1) Quelle est la nature de l'ensemble $\mathcal{E}$ dans chacun des cas suivants :
$a)\ m=0\ ?\qquad b)\ m=2\ ?\qquad c)\ m=3\ ?$
2) Peut-on déterminer le réel $m$ pour que l'origine $O$ du repère appartienne à l'ensemble $\mathcal{E}$ ?
3) Existe-t-il un ensemble $\mathcal{E}$ contenant le point $H(4\;;\ -2)$ ?
4) pour quelles valeurs de $m$ l'ensemble $\mathcal{E}$ est-t-il un cercle ?
Préciser alors son centre $\Omega$ et son rayon $r$ en fonction de $m$.
5) Montrer que, lorsque $m$ varie, l'ensemble des centres $\Omega$ de ces cercles est un segment de droite.
Exercice 36
Dans chacun des cas suivants, déterminer une équation du ou des cercles déterminés par les conditions :
1) $\mathcal{C}$ a pour centre $A(1\;,\ 1)$ et passe par $B(2\;,\ 3)$.
2) $\mathcal{C}$ a pour centre $\Omega(2\;,\ 0)$ et est tangent à la droite d'équation $x+y+1=0$.
3) $\mathcal{C}$ passe par $A(1\;,\ 0)\;;\ B(0\;,\ 2)\;;\ C(1\;,\ 2)$.
4) $\mathcal{C}$ a pour diamètre $[AB]\text{ avec }A(3\;,\ 2)\text{ et }B(-1\;,\ 5)$.
5) $\mathcal{C}$ est circonscrit au triangle $ABC\text{ avec }A(2\;,\ 3)\;;\ B(-2\;,\ -1)\;;\ C(1\;,\ -1)$.
Exercice 37
Puissance d'un point par rapport à un cercle
A) Puissance d'un point par rapport à un cercle et lignes de niveau
Dans un plan $P$, soit un cercle $\mathcal{C}$ de centre $\Omega$ et de rayon $R\text{ et }M$ un point quelconque.
On mène par $M$ une sécante au cercle $\mathcal{C}$ qui le coupe en deux points $A\text{ et }B.$
$A'$ est le point du cercle $\mathcal{C}$ diamétralement opposé à $A$.
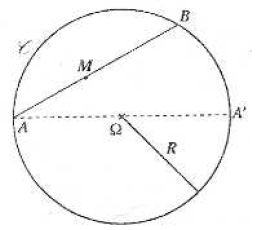
1) a) Établir que $\overrightarrow{MA}\cdot\overrightarrow{MB}=\overrightarrow{MA}\cdot\overrightarrow{MA'}$
b) Montrer alors que $\overrightarrow{MA}\cdot\overrightarrow{MB}=\Omega M^{2}-R^{2}$
c) En déduire que ce produit scalaire est indépendant de la sécante issue de $M.$
2) On pose $\Phi(M)=\Omega M^{2}-R^{2}$.
Le réel $\Phi(M)$ est appelé la puissance du point $M$ par rapport au cercle $\mathcal{C}$.
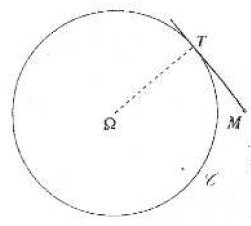
a) Lorsque $M$ est un point extérieur au cercle $\mathcal{C}$,
on considère la tangente $(MT)$ au cercle $\mathcal{C}\text{ en }T.$
Montrer que $\Phi(M)=MT^{2}$.
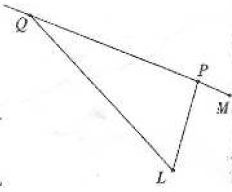
b) Soit un triangle $MQL\text{ et }M$ un point de la droite $(PQ)$ tel que l'on ait :
$\overline{MP}\times \overline{MQ}=ML^{2}.$
Montrer que le cercle circonscrit au triangle $PQL$ est tangent en $L$ à la droite $(ML)$
3) Étudier le signe de $\Phi(M)$ suivant la position de $M$ dans le plan $\mathcal{P}$.
4) Soit $\mathcal{L}_{k}$ la ligne de niveau $k$ de l'application $$\Phi\ :\ M\mapsto \Phi(M)=\Omega M^{2}-R^{2}$$
$\mathcal{L}_{k}$ est donc l'ensemble des points $M$ tels que $\Phi(M)=k.$
a) Discuter suivant les valeurs de $k$ la nature de la ligne $\mathcal{L}_{k}$.
b) Déterminer et, lorsqu'elle existe, représenter $\mathcal{L}_{k}$ pour les valeurs suivantes de $k\ :$
$k=-2R^{2}\;,\ k=-\dfrac{3}{4}R^{2}\text{ et }k=0$
c) Déterminer l'ensemble $\mathcal{E}$ des points $M$ du plan $\mathcal{P}$ tels que :
$$R^{2}\leq \Phi(M)\leq 3R^{2}.$$
On retiendra de cette étude les résultats suivants :
B) Axe radical de deux cercles
On considère deux cercles de centres distincts :
$\mathcal{C}_{1}$ de centre $\Omega_{1}$ et de rayon $R_{1}$, et
$\mathcal{C}_{2}$ de centre $\Omega_{2}$ et de rayon $R_{2}$.
On note $\Phi_{1}(M)$, respectivement $\Phi_{2}(M)$, les puissances de $M$ par rapport aux cercles $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$.
1) a) Montrer que l'ensemble $\Delta$ des points $M$ du plan tels que
$\Phi_{1}(M)=\Phi_{2}(M)$, est une droite perpendiculaire à la droite $(\Omega_{1}\Omega_{2})$.
b) Cette droite est appelée axe radical des cercles $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$.
Quel est l'axe radical de deux cercles sécants en $A\text{ et }B$ ?
2) Construire $\Delta$ dans les cas suivants (on suppose que l'unité choisie est le centimètre) :
$a)\ R_{1}=2\;,\ R_{2}=5\text{ et }\Omega_{1}\Omega_{2}=7\;;\qquad b)\ R_{1}=3\;,\ R_{2}=4\text{ et }\Omega_{1}\Omega_{2}=7$.
3) On considère maintenant trois cercles dont les centres sont distincts et non alignés :
$\mathcal{C}_{1}$ de centre $\Omega_{1}$ et de rayon $R_{1}$,
$\mathcal{C}_{2}$ de centre $\Omega_{2}$ et de rayon $R_{2}$,
$\mathcal{C}_{3}$ de centre $\Omega_{3}$ et de rayon $R_{3}$.
Soit $\Delta_{1}$ l'axe radical des cercles $\mathcal{C}_{2}\text{ et }\mathcal{C}_{3}$,
$\Delta_{2}$ l'axe radical des cercles $\mathcal{C}_{1}\text{ et }\mathcal{C}_{3}$,
$\Delta_{3}$ l'axe radical des cercles $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$.
a) Montrer que les droites $\Delta_{1}\;,\ \Delta_{2}\text{ et }\Delta_{3}$ sont concourantes en un point $O$.
Ce point est appelé centre radical des trois cercles $\mathcal{C}_{1}\;,\ \mathcal{C}_{2}\text{ et }\mathcal{C}_{3}$.
b) Application :
construction de l'axe radical de deux cercles n'ayant aucun point commun.
Soit $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$ deux cercles de centres $\Omega_{1}\text{ et }\Omega_{2}$ et de rayons $R_{1}\text{ et }R_{2}$ avec :
$R_{1}=3\;,\ R_{2}=2\text{ et }\Omega_{1}\Omega_{2}=7$.
En utilisant un cercle $\mathcal{C}_{3}$ convenablement choisi, déterminer un point de l'axe radical de $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$.
Construire alors cet axe.
c) Démontrer que le centre radical de trois cercles est soit intérieur aux trois cercles, soit extérieur aux trois cercles, soit sur les trois cercles.
C) Cercles orthogonaux
1) Soit $\mathcal{C}_{1}$ un cercle de centre $\Omega_{1}$ et de rayon $R_{1}$.
Soit $\mathcal{C}_{2}$ un cercle de centre $\Omega_{2}$ et de rayon $R_{2}$.
Donner un encadrement de la distance $\Omega_{1}\Omega_{2}$ de façon à ce que les cercles $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$ soient sécants.
2) Le plan $\mathcal{P}$ est rapporté à un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j})$
On définit les cercles $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$ par les équations cartésiennes suivantes :
$\mathcal{C}_{1}\ :\ x^{2}+y^{2}+4x-y-2=0\text{ et }\mathcal{C}_{2}\ :\ x^{2}+y^{2}-6x-6y-7=0$.
a) Déterminer les coordonnées des points $\Omega_{1}\text{ et }\Omega_{2}$ et calculer $R_{1}$, puis $R_{2}$.
b) En utilisant la question 1), montrer que $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$ sont sécants.
c) Soit $I\text{ et }J$ les points d'intersection des cercles $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$, $I$ désignant le point d'intersection d'abscisse nulle.
Déterminer les coordonnées de $I\text{ et }J$.
d) Déterminer une équation de la tangente au cercle $\mathcal{C}_{1}\text{ en }I$, ainsi qu'une équation de la tangente au cercle $\mathcal{C}_{2}\text{ en }I$.
Montrer alors que $\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}$ sont orthogonaux.
e) Calculer la puissance du point $\Omega_{1}$ par rapport au cercle $\mathcal{C}_{2}$, et la puissance du point $\Omega_{2}$ par rapport au cercle $\mathcal{C}_{1}$.
Comparer les nombres obtenus.
f) Soit $D$ la droite passant par $\Omega_{1}$ et parallèle à l'axe $(O\;,\ \vec{i})$
Donner les coordonnées des points d'intersection
$P_{1}\text{ et }Q_{1}\text{ de }D$ avec le cercle $\mathcal{C}_{1}$, puis les coordonnées des points d'intersection
$P_{2}\text{ et }Q_{2}\text{ de }D$ avec le cercle $\mathcal{C}_{1}$.
Montrer alors que :
$$\Omega_{1} P_{1}^{2}=\Omega_{1} Q_{1}^{2}=\overrightarrow{\Omega_{1}P_{2}}\cdot\overrightarrow{\Omega_{1}Q_{2}}$$
Correction des exercices

Commentaires
Fiacre Martin D... (non vérifié)
ven, 11/15/2019 - 01:00
Permalien
format pdf
Fiacre Martin D... (non vérifié)
ven, 11/15/2019 - 01:09
Permalien
corrections des exercices
garad (non vérifié)
lun, 02/07/2022 - 18:04
Permalien
pouvoir imprimer les exo
garad (non vérifié)
lun, 02/07/2022 - 18:04
Permalien
pouvoir imprimer les exo
diomaye Thiao (non vérifié)
mar, 05/31/2022 - 15:26
Permalien
correction exercice 32
diomaye Thiao (non vérifié)
mar, 05/31/2022 - 15:27
Permalien
correction de exercice 32
Anonyme (non vérifié)
mer, 01/11/2023 - 22:41
Permalien
je trouve les exercices
balthazar (non vérifié)
dim, 01/05/2025 - 18:44
Permalien
400
Ajouter un commentaire