Solution des exercices : Repérage dans le plan - 5e
Classe:
Cinquième
Exercice 1 "Repérage sur une droite ; calcul de la distance de deux points"
1) Donnons les abscisses qui correspondent aux points $G\;,\ F\;,\ E\;,\ O\ $ et $\ A.$
En graduant la droite $(x'x)$ d'unité $OA$, on obtient :
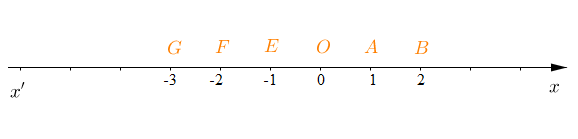
On remarque alors que :
$-3$ est l'abscisse du point $G$
$-2$ est l'abscisse du point $F$
$-1$ est l'abscisse du point $E$
$0$ est l'abscisse du point $O$
$1$ est l'abscisse du point $A$
2) Calculons les distances : $OA\;;\ OB\ $ et $\ OG.$
On rappelle que sur une droite graduée, pour calculer la distance entre deux points $O\ $ et $\ M$, on compare d'abord les abscisses de $O\ $ et $\ M$ puis on calcule la différence entre la plus grande abscisse et la plus petite abscisse.
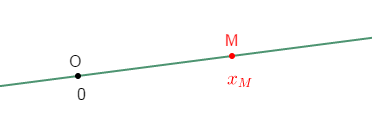
$\centerdot\ $ Calcul de la distance $OA$
Comme l'abscisse du point $O$ est zéro $(0)$ alors, $O$ est origine du repère.
D'après le résultat de la question $1)$, on a : l'abscisse du point $O$ est zéro $(0)$ et l'abscisse du point $A$ est égale à $1.$
Alors, on constate que l'abscisse du point $A$ est plus grande que l'abscisse du point $O.$
Donc, la distance $OA$ est donnée par :
$\begin{array}{rcl} OA&=&x_{A}-x_{O}\\ \\&=&1-0\\ \\&=&1\end{array}$
D'où, $\boxed{OA=1}$
$\centerdot\ $ Calcul de la distance $OB$
On a : l'abscisse du point $O$ est égale $0$ et l'abscisse du point $B$ est égale à $2.$
On remarque alors que l'abscisse du point $B$ est plus grande que l'abscisse du point $O.$
Donc, la distance $OB$ est donnée par :
$\begin{array}{rcl} OB&=&x_{B}-x_{O}\\ \\&=&2-0\\ \\&=&2\end{array}$
D'où, $\boxed{OB=2}$
$\centerdot\ $ Calcul de la distance $OG$
Soit $x_{G}=-3$ l'abscisse du point $G\ $ et $\ x_{O}=0$ l'abscisse du point $O.$
Alors, on constate que l'abscisse du point $O$ est plus grande que l'abscisse du point $G.$
Donc, la distance $OG$ est donnée par :
$\begin{array}{rcl} OG&=&x_{O}-x_{G}\\ \\&=&0-(-3)\\ \\&=&0+(+3)\\\\&=&+3\end{array}$
D'où, $\boxed{OG=3}$
3) Calculons les distances : $GB\;;\ EB\ $ et $\ FB.$
On rappelle que sur une droite graduée, pour calculer la distance entre deux points $M\ $ et $\ N$, on compare d'abord les abscisses de $M\ $ et $\ N$ puis on calcule la différence entre la plus grande abscisse et la plus petite abscisse.
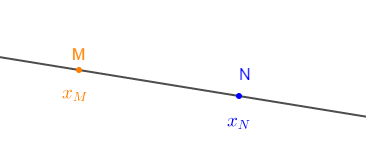
$\centerdot\ $ Calcul de la distance $GB$
On a : $x_{B}=2\ $ et $\ x_{G}=-3.$
On constate alors que l'abscisse du point $B$ est plus grande que l'abscisse du point $G.$
Donc, la distance $GB$ est donnée par :
$\begin{array}{rcl} GB&=&x_{B}-x_{G}\\ \\&=&2-(-3)\\ \\&=&2+(+3)\\\\&=&2+3\\\\&=&5\end{array}$
D'où, $\boxed{GB=5}$
$\centerdot\ $ Calcul de la distance $EB$
On a : $x_{B}=2\ $ et $\ x_{E}=-1.$
Alors, on remarque que l'abscisse du point $B$ est plus grande que l'abscisse du point $E.$
Donc, la distance $EB$ est donnée par :
$\begin{array}{rcl} EB&=&x_{B}-x_{E}\\ \\&=&2-(-1)\\ \\&=&2+(+1)\\ \\&=&2+1\\\\&=&3\end{array}$
Ainsi, $\boxed{EB=3}$
$\centerdot\ $ Calcul de la distance $FB$
Comme $x_{B}=2\ $ et $\ x_{F}=-2$ alors, on remarque que l'abscisse du point $B$ est plus grande que l'abscisse du point $F.$
Donc, la distance $FB$ est donnée par :
$\begin{array}{rcl} FB&=&x_{B}-x_{F}\\ \\&=&2-(-2)\\ \\&=&2+(+2)\\ \\&=&2+2\\\\&=&4\end{array}$
Par suite, $\boxed{FB=4}$
Exercice 2
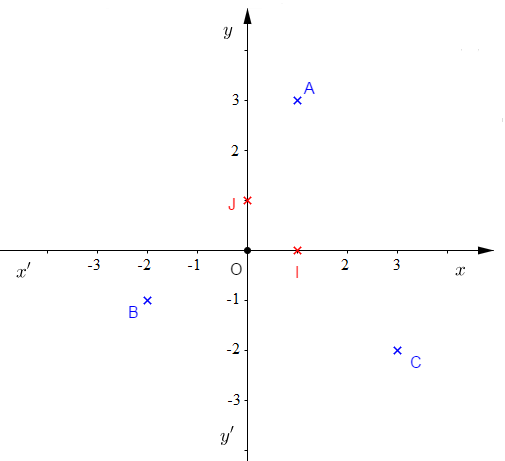
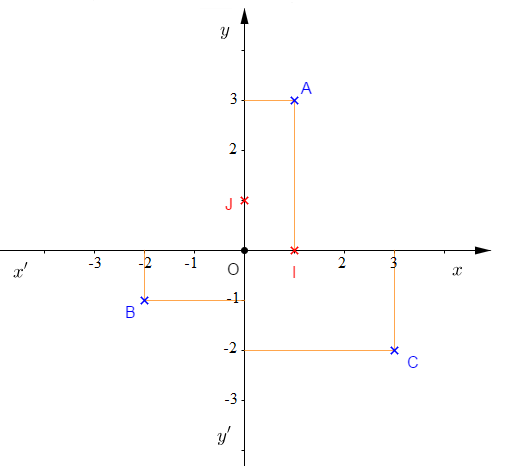
On considère le repère orthonormé $(O\;;\ I\;,\ J)$ ci-dessous.
1) a) Le point $O$ est appelé origine du repère orthonormé $(O\;;\ I\;,\ J)$
b) Pour le repère orthonormé $(O\;;\ I\;,\ J)\ :$
$-\ $ la droite $(xx')$ est appelée axe des abscisses d'origine $O$ et d'unité $OI$
$-\ $ la droite $(yy')$ est appelée axe des ordonnées d'origine $O$ et d'unité $OJ$
2) Déterminons graphiquement les coordonnées des points : $A\;,\ B\;,\ C\;,\ O\;,\ I\ $ et $\ J.$
$\centerdot\ $ soit $x_{A}\ $ et $\ y_{A}$ du point $A$ où, $x_{A}$ est l'abscisse du point $A$ et $\ y_{A}$ son ordonnée.
En partant du point $A$, on trace une droite parallèle à l'axe $(yy').$ Cette droite coupe l'axe $(xx')$ à la valeur $1.$
Cette valeur représente donc l'abscisse du point $A\ :\ x_{A}=1$
De la même manière, en partant du point $A$, on peut tracer une droite parallèle à l'axe $(xx').$ Cette droite coupe l'axe $(yy')$ à la valeur $3.$
Cette valeur représente donc l'ordonnée du point $A\ :\ y_{A}=3$
Donc, les coordonnées du point $A$ sont données par :
$$x_{A}=1\quad\text{et}\quad y_{A}=3$$
D'où,
$$A(1\;,\ 3)$$
$\centerdot\ $ soit $x_{B}\ $ et $\ y_{B}$ du point $B$ avec, $x_{B}$ l'abscisse du point $B$ et $\ y_{B}$ son ordonnée.
En procédant de la même manière on obtient :
$$x_{B}=-2\quad\text{et}\quad y_{B}=-1$$
Ainsi,
$$B(-2\;,\ -1)$$
$\centerdot\ $ soit $x_{C}\ $ et $\ y_{C}$ du point $C$ avec, $x_{C}$ l'abscisse du point $C$ et $\ y_{C}$ son ordonnée.
En procédant de la même manière on obtient :
$$x_{C}=3\quad\text{et}\quad y_{C}=-2$$
Donc,
$$C(3\;,\ -2)$$
$\centerdot\ $ Comme le point $O$ est origine du repère $(O\;;\ I\;,\ J)$ alors, les coordonnées du point $O$ sont :
$$(0\;,\ 0)$$
$\centerdot\ $ le point $I$ est sur l'axe $(xx')$ et d'abscisse $1$ donc, ses coordonnées sont données par :
$$x_{I}=1\quad\text{et}\quad y_{I}=0$$
Donc,
$$I(1\;,\ 0)$$
$\centerdot\ $ le point $J$ étant sur l'axe $(yy')$ et d'ordonnée $1$ donc, ses coordonnées sont données par :
$$x_{J}=0\quad\text{et}\quad y_{J}=1$$
Par suite,
$$J(0\;,\ 1)$$
Auteur:
Diny Faye

Commentaires
Malfred (non vérifié)
dim, 09/11/2022 - 22:57
Permalien
Mettre comme notation des
Seynabou dion (non vérifié)
ven, 03/14/2025 - 15:11
Permalien
Apprendre
Ajouter un commentaire