Série d'exercices : Amplificateur opérationnel - 2nd S
Classe:
Seconde
Exercice 1
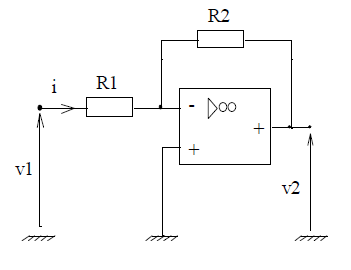
$R_{1}=1\;k\Omega\;,\ R_{2}=12\;k\Omega$
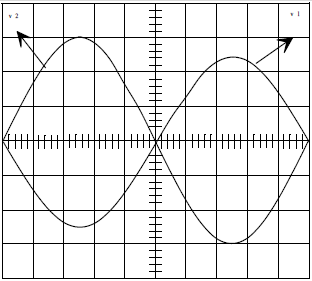
Calibre : $v_{1}\ :\ 0.2\;V/div\;;\quad v_{2}\ :\ 2\;V/div$
Balayage : $0.5\;ms/div$
1) Déterminer $V_{1}\;,\ V_{2}$ et l'amplification du montage $A=\dfrac{V_{2}}{V_{1}}$
Comment appelle-t-on ce montage ?
2) L'amplificateur Opérationnel fonctionne en régime linéaire .
Pourquoi ? Que peut on dire de $v_{d}$ (ou $\varepsilon$) ?
3) Que dire des courants $i_{_{R_{1}}}\ $ et $\ i_{_{R_{2}}}.$ Justifier.
4) Écrire les lois des mailles d'entrée et de sortie. En déduire $A=\dfrac{V_{2}}{V_{1}}$ en fonction de $R_{1}\ $ et $\ R_{2}.$
5) $v_{\text{sat}}=\pm 12\;V.$ Calculer $v_{1_{\text{max}}}$ pour éviter la saturation.
Tracer $v_{2}(t)$ ci-dessous (l'amplitude de $v_{1}$ est maintenant réglée à $1.5\;V).$
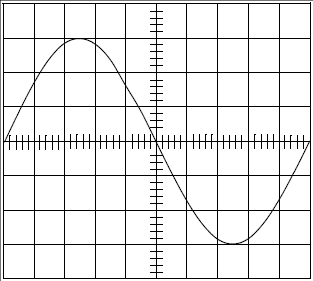
Calibre : $v_{1}\ :\ 0.5\;V/div\;;\quad v_{2}\ :\ 5\;V/div$
Balayage : $0.5\;ms/div$
Exercice 2
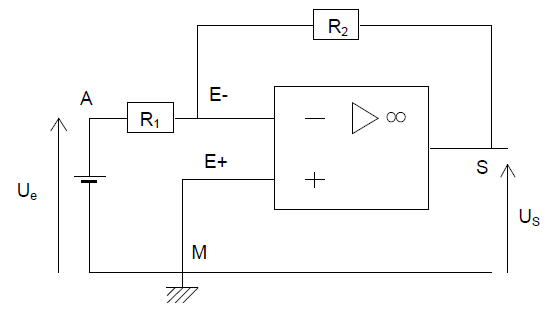
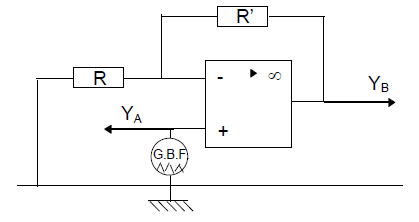
On considère le montage ci-dessus pour lequel l'amplificateur opérationnel $(A.O.)$ est supposé idéal.
La tension de saturation de l'$A.O.$ est $V_{\text{sat}}=15\;V.$
On donne les résistances : $R_{1}=2.2\;k\Omega\;,\ R_{2}=4.7\;k\Omega$
La tension d'entrée est $U_{e}=U_{_{AM}}=1.5\;V.$
1) Préciser ce qui définit un $A.O.$ idéal.
2.1) Montrer qu'avec ce montage un même courant traverse $R_{1}\ $ et $\ R_{2}.$
2.2) Établir que, dans les conditions considérées, la tension de sortie $U_{s}=U_{_{SM}}$ est donnée par : $U_{s}=-\dfrac{R_{2}}{R_{1}}U_{e}$
2.3) Justifier le nom de montage amplificateur inverseur donné à ce montage.
2.4) Calculer la tension de sortie.
3) Entre $A\ $ et $\ M$, à l'entrée du montage précédent, on remplace la pile par un générateur de tension réglable.
Compléter le tableau ci-dessous en précisant, pour chaque valeur de la tension d'entrée $U_{e}$ la valeur correspondante de la tension de sortie $U_{s}.$
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|}\hline U_{e}(V)&-10&-8.0&-4.0&-2.0&0.0&2.0&4.0&8.0&10\\ \hline U_{s}(V)&&&&&&&&&\\ \hline\end{array}$$
Exercice 3
Le montage étudié dans cette partie est représenté sur la figure 1.
L'amplificateur opérationnel $AO_{1}$ utilisé est considéré comme parfait.
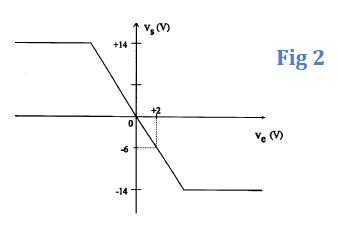
La caractéristique $V_{s}=f(V_{e})$ du montage est représentée sur la figure 2.
La résistance $R_{1}$ est ajustable et $R_{2}=10\;k\Omega.$
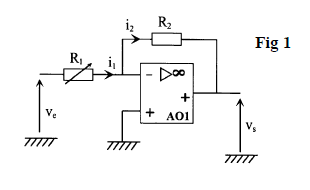
1) Montrer qu'en régime linéaire l'amplification du montage peut s'exprimer sous la forme :
$$A=\dfrac{V_{s}}{V_{e}}=-\dfrac{R_{2}}{R_{1}}$$
2) En utilisant le résultat précédent et la caractéristique de la figure 2, déterminer la valeur donnée à la résistance $R_{1}.$
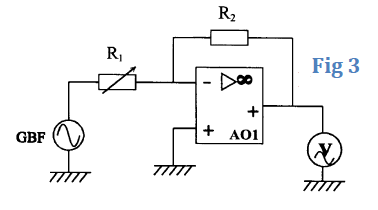
3) On applique à l'entrée du montage une tension sinusoïdale de valeur efficace $V_{_{E}}=2.0\;V.$
Un voltmètre est utilisé en en position $AC$ conformément à la figure 3. Quelle est l'indication de cet appareil
Exercice 4
On réalise avec le même montage deux séries de mesures :
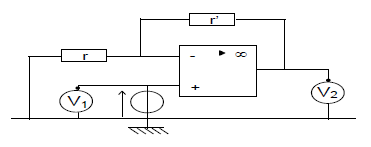
$\centerdot\ $ première série : le voltmètre $n^{\circ}1$ indique $2.3\;V$ et le voltmètre $n^{\circ}2$ affiche $9.2\;V$ ;
$\centerdot\ $ deuxième série : le voltmètre $n^{\circ}1$ indique$4.1\;V$ et le voltmètre $n^{\circ}2$ affiche $13.6\;V$
1) Comment s'appelle la tension mesurée par le voltmètre $n^{\circ}1\ ?$
2) Comment s'appelle la tension mesurée par le voltmètre $n^{\circ}2\ ?$
3) Quel est le coefficient d'amplification du montage ?
Justifiez le choix de la série de mesures que vous utilisez pour cette détermination.
4) Quelle est la tension de saturation du montage ?
Exercice 5
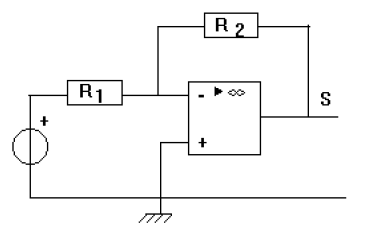
$R_{1}=10\;k\Omega\;;\quad R_{2}=33\;k\Omega$
Pour ce montage, le coefficient d'amplification vaut : $A=-\dfrac{R_{2}}{R_{1}}$ et la tension de saturation $\pm 14\;V$
1) On appelle $U_{e}$ la tension d'entrée du montage et $U_{s}$, la tension de sortie.
Reporter sur le montage les flèches tension $U_{e}\ $ et $\ U_{s}.$
2) Calculer $A.$
Lorsque le montage amplificateur fonctionne en régime linéaire, écrire la relation qui existe entre la tension de sortie $U_{s}$ et la tension d'entrée $U_{e}.$
3) Compléter le tableau de valeurs :
$$\begin{array}{|l|c|c|c|c|c|c|c|}\hline U_{e}(V)&-6&-4&-2&0&1&3&5\\ \hline U_{s}(V)&&&&&&&\\ \hline\end{array}$$
4) Construire le graphique de la fonction $U_{s}=f(U_{e})$ ;
5) A partir de cette courbe, préciser :
$-\ \ $ les valeurs de $U_{e}$ pour lesquelles le régime de fonctionnement est appelé linéaire.
$-\ \ $ les valeurs de $U_{e}$ pour lesquelles le régime de fonctionnement est dit saturé
Exercice 6
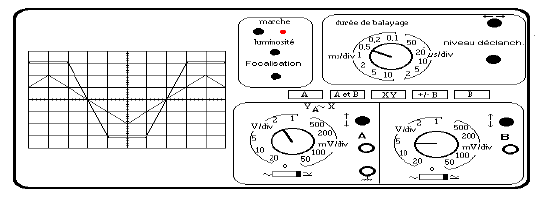
On réalise le montage suivant et on observe les deux oscillogrammes ci-dessous :
Déterminer :
1) la tension de saturation :
2) le coefficient d'amplification du montage.
Sur le montage, le symbole « masse » figure à la fois la masse du circuit et celle des deux voies de l'oscilloscope.
Les réglages initiaux de l'oscilloscope, pour chaque voie, sont tels que la ligne médiane horizontale corresponde à une tension nulle.
Exercice 7
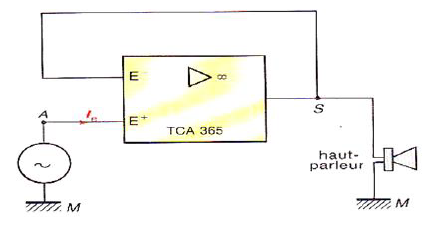
1) Rappeler les caractéristiques d'un $A.O.$ idéal.
2) Quelle relation simple existe-t-il entre la tension $U_{e}$ et la tension $U_{s}\ ?$
Exercice 8
A l'aide d'un amplificateur opérationnel alimenté par un générateur $(e_{1}\;,\ 0\;,\ -e_{2})$, nous avons réalisé le montage de la figure ci-dessous
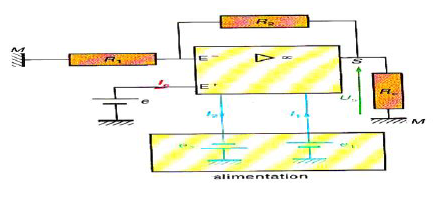
1) En supposant l'$A.O.$ idéal $(I^{+}=I^{-}=0\;;\ V_{_{E^{+}}}-V_{_{E^{-}}}=0$ montrer que :
$$\dfrac{U_{s}}{e}=\dfrac{R_{1}+R_{2}}{R_{1}}$$
Application numérique : $R_{1}=10\;k\Omega\;;\quad R_{2}=100\;k\Omega$
2) Avec un $A.O.\ 741$, on a relevé les mesures suivantes :
$I_{e}=0.004\;\mu A\;;\ e=0.48\;V\;;\ U_{s}=5.4\;V$
$R_{c}=2000\Omega\;;\ e_{1}=15.13\;V\;;\ I_{1}=4.23\;mA\;;\ e_{2}=15.10\;V\;;\ I_{2}=1.50\;mA$
Calculer le rapport expérimental $\dfrac{U_{s}}{e}.$
Conclure.
Exercice 9
Pour le montage de la figure ci-dessous, on donne :
$R_{1}=10\;k\Omega\;;\ R_{2}=4.7\;k\Omega\ $ et $\ R_{3}=2.2\;k\Omega$
De plus, la mesure de $i_{c}$ a donné : $i_{c}=2.5\;mA$
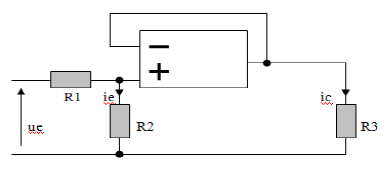
1) l'ampli op fonctionne-t-il en régime linéaire ou saturé ?
Justifier.
2) calculer l'intensité $i_{e}$ du courant dans la résistance $R_{2}.$
3) calculer la tension d'entrée $u_{e}.$
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Commentaires
iv (non vérifié)
sam, 05/23/2020 - 09:00
Permalien
correction
Michel (non vérifié)
ven, 06/18/2021 - 16:14
Permalien
Pc
Bari (non vérifié)
ven, 10/14/2022 - 02:55
Permalien
Image
Kaboré harouna (non vérifié)
jeu, 01/30/2025 - 00:53
Permalien
Demande de correction
Ajouter un commentaire