Solutions exercices : Calcul vectoriel - 2nd

Classe: 
Seconde
 

Exercice 1

a) 

b) 

 

c)

d)

e)

f)

g)

h)

 

Exercice 2

 

Exercice 3

a) On construit successivement deux parallélogrammes, le premier sur $\vec{u}$ et $\vec{v}$, dont la diagonale donne le vecteur $\vec{u}+\vec{v}$, puis le second sur $\vec{u}+\vec{v}$ et $\vec{w}$, dont la diagonale donne le vecteur $\vec{u}+\vec{v}+\vec{w}.$

 
 
b) On construit $\vec{u}+\vec{v}$ puis, "au bout" de ce vecteur, on construit un représentant du vecteur $\vec{w}.$

 

 
c) 

 

d) 


 
Ici, on remarque que $\vec{u}+\vec{w}=\vec{0}$, de sorte que $\vec{u}+\vec{v}+\vec{w}=\vec{v}\ !$

Exercice 4

$\centerdot\ E$ est un point de $(AB)$ et $\overrightarrow{AE}$ a le même sens que $\overrightarrow{AB}$, donc $E\in[AB).$ On partage $[AB]$ en trois parties de même longueur (voir le programme de Troisième) et on compte cette longueur quatre fois à partir de $A.$ 


 
$\centerdot\ F$ est sur la parallèle à $(AC)$ passant par $B$ et $\overrightarrow{BF}$ a le sens contraire de $\overrightarrow{AC}.$ On partage $[AC]$ en deux parties et on prend une fois cette longueur à partir de $B.$

Exercice 5



 
A partir d'un point arbitraire $A$, tracer une parallèle à la direction de $\vec{u}$, puis construire le vecteur $5\vec{u}$ par la méthode de l'exercice précédent (reporter 5 fois la longueur de $\vec{u}$ dans le même sens).
 
Puis, à l'extrémité du vecteur ainsi obtenu, tracer la demi-droite parallèle et de sens contraire à $\vec{v}$, puis reporter sur cette demi-droite 3.5 fois la longueur de $\vec{v}.$ On obtient le vecteur $\dfrac{7}{2}\vec{v}.$
 
En joignant l'origine du premier vecteur à l'extrémité du second, on obtient le vecteur $5\vec{u}-\dfrac{7}{2}\vec{v}.$
 
La méthode est la même pour le vecteur $-3\vec{u}+2\vec{v}.$

Exercice 6

 
 
 
 

Exercice 7

 
 

 

Exercice 8

a) $\overrightarrow{IL}=\overrightarrow{IK}+\overrightarrow{KL}\quad$ b) $\overrightarrow{CD}=\overrightarrow{CE}+\overrightarrow{ED}$ 
 
c) $\overrightarrow{CD}=\overrightarrow{CJ}+\overrightarrow{JD}\quad$ d) $\overrightarrow{CD}=\overrightarrow{CH}+\overrightarrow{HD}$
 
e) $\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}\quad$ f) $\overrightarrow{HD}=\overrightarrow{HB}+\overrightarrow{BD}$ 
 
g) $\overrightarrow{PQ}=\overrightarrow{PA}+\overrightarrow{AQ}\quad$ h) $\overrightarrow{AQ}=\overrightarrow{AB}+\overrightarrow{BQ}$
 
i) $\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DJ}+\overrightarrow{JH}=\overrightarrow{AH}\quad$ j) $\overrightarrow{AB}=\overrightarrow{AK}+\overrightarrow{KP}+\overrightarrow{PB}$ 
 
k) $\overrightarrow{BA}=\overrightarrow{BD}+\overrightarrow{DC}+\overrightarrow{CA}$

Exercice 9

 

 
 
1) $\overrightarrow{AE}+\overrightarrow{AF}=\overrightarrow{AI}\quad$ 2) $\overrightarrow{AE}+\overrightarrow{EK}=\overrightarrow{AK}$ 
 
3) $\overrightarrow{EG}+\overrightarrow{GE}=\vec{0}\quad$ 4) $\overrightarrow{EG}+\overrightarrow{AF}=\overrightarrow{EK}$

Exercice 10

a) On introduit $A$ dans le vecteur $\overrightarrow{MB}$ par la relation de Chasles, puis on développe en utilisant les propriétés du calcul vectoriel.
 
$\begin{array}{rcl} \overrightarrow{MA}+3\overrightarrow{MB}=\vec{0}&\Leftrightarrow&\overrightarrow{MA}+3(\overrightarrow{MA}+\overrightarrow{AB})=\vec{0}\\ \\ &\Leftrightarrow&\overrightarrow{MA}+3\overrightarrow{MA}+3\overrightarrow{AB}=\vec{0}\\ \\ &\Leftrightarrow&4\overrightarrow{MA}+3\overrightarrow{AB}=\vec{0}\end{array}$
 
b) La relation $4\overrightarrow{MA}+3\overrightarrow{AB}=\vec{0}$ s'écrit aussi $3\overrightarrow{AB}=-4\overrightarrow{MA}=4\overrightarrow{AM}$ ou encore $\overrightarrow{AM}=\dfrac{3}{4}\overrightarrow{AB}$
 
Construction du point $M$
 
 

Exercice 11

a) $\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{BJ}\quad$ b) $\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}$ 
 
c) $\overrightarrow{MN}=\overrightarrow{MP}+\overrightarrow{PN}\quad$ d) $\overrightarrow{FE}=\overrightarrow{FP}+\overrightarrow{PG}+\overrightarrow{GE}$
 
e) $\overrightarrow{HJ}=\overrightarrow{HI}+\overrightarrow{IJ}\quad$ f) $\overrightarrow{JM}=\overrightarrow{JK}+\overrightarrow{KM}$ 
 
g) $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{BC}=\overrightarrow{AD}\quad$ h) $\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}$

Exercice 12

1) En suivant la suggestion de l'énoncé, on a : $\vec{v}_{_{M}}=2\overrightarrow{MA}-5(\overrightarrow{MA}+\overrightarrow{AB})+3(\overrightarrow{MA}+\overrightarrow{AC}).$ Après simplification, les termes "en $\overrightarrow{MA}$"disparaissent et on obtient : $\vec{v}_{_{M}}=-5\overrightarrow{AB}+3\overrightarrow{AC}\ :$  c'est bien un vecteur constant car la lettre $M$ ne figure plus dans cette écriture
 
2) Méthode analogue au 1) ; on trouve que ce vecteur est égal à $\overrightarrow{AB}+2\overrightarrow{AC}$

Exercice 13

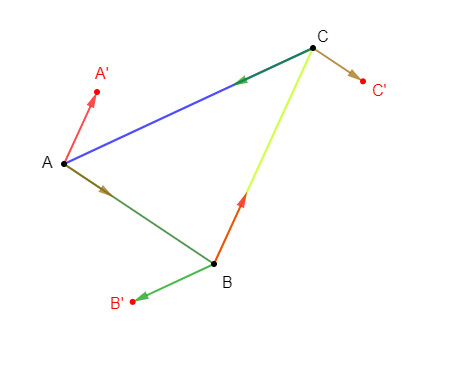
On donne un triangle $ABC$. On considère les points $A'\;,\ B'\ $ et $\ C'$ tels que : $$\overrightarrow{AA'}=\dfrac{1}{3}\overrightarrow{BC}\;,\quad \overrightarrow{BB'}=\dfrac{1}{3}\overrightarrow{CA}\;,\quad \overrightarrow{CC'}=\dfrac{1}{3}\overrightarrow{AB}$$
Démontrons que :
$$\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\vec{0}$$
Pour cela, calculons directement la somme vectorielle suivante :
$$\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}$$
Dans cette relation, remplaçons :
 
$\overrightarrow{AA'}$ par $\dfrac{1}{3}\overrightarrow{BC}$
 
$\overrightarrow{BB'}$ par $\dfrac{1}{3}\overrightarrow{CA}$
 
$\overrightarrow{CC'}$ par $\dfrac{1}{3}\overrightarrow{AB}$
 
On obtient alors :
$$\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\dfrac{1}{3}\overrightarrow{BC}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}$$
Puis, en appliquant la relation de Chasles et les propriétés du calcul vectoriel, on trouve :
 
$\begin{array}{rcl} \overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}&=&\dfrac{1}{3}\overrightarrow{BC}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\\\\&=&\dfrac{1}{3}\left(\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}\right)\\\\&=&\dfrac{1}{3}\left(\underbrace{\overrightarrow{BA}+\overrightarrow{AB}}_{=\vec{0}}\right)\\\\&=&\dfrac{1}{3}\times\vec{0}\\\\&=&\vec{0}\end{array}$
 
D'où, $\boxed{\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\vec{0}}$
 
 

Exercice 14

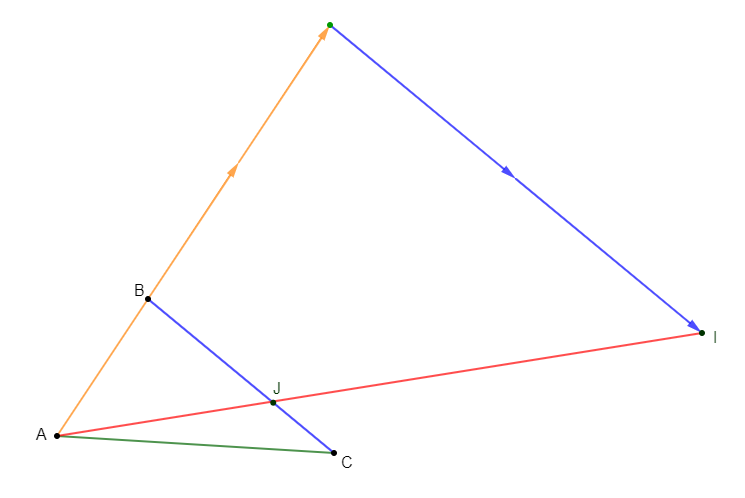
$ABC$ est un triangle. $J$ est le point tel que $\overrightarrow{BJ}=\dfrac{2}{3}\overrightarrow{BC}.$
 
1) Exprimons $\overrightarrow{AJ}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}.$
 
En effet, on a : $\overrightarrow{BJ}=\dfrac{2}{3}\overrightarrow{BC}.$
 
Donc, en introduisant le point $A$ dans le vecteur $\overrightarrow{BJ}$ par la relation de Chasles, on obtient :
$$\overrightarrow{BA}+\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{BC}$$
Par suite, en utilisant les propriétés du calcul vectoriel, on trouve :
 
$\begin{array}{rcl} \overrightarrow{BA}+\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{BC}&\Leftrightarrow&\overrightarrow{AJ}=-\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\\\\&\Leftrightarrow&\overrightarrow{AJ}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\end{array}$
 
Ainsi, $\boxed{\overrightarrow{AJ}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}}$
 
2) Soit $I$ le point tel que $\overrightarrow{AI}=3\overrightarrow{AB}+2\overrightarrow{BC}.$
 
Montrons que les points $A\;,\ I\ $ et $\ J$ sont alignés.
 
On a :
 
$\overrightarrow{AJ}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}$
 
$\overrightarrow{AI}=3\overrightarrow{AB}+2\overrightarrow{BC}$
 
Donc, dans la base $\left(\overrightarrow{AB}\;,\ \overrightarrow{BC}\right)$, les coordonnées des vecteurs $\overrightarrow{AJ}\ $ et $\ \overrightarrow{AI}$ sont données par :
$$\overrightarrow{AJ}\begin{pmatrix}1\\ \\\dfrac{2}{3}\end{pmatrix}\ \text{ et }\ \overrightarrow{AI}\begin{pmatrix}3\\ \\2\end{pmatrix}$$
Calculons alors les rapports : $\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AJ}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AJ}}}}$
 
On a :
 
$\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AJ}}}}=\dfrac{3}{1}=3$
 
$\dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AJ}}}}=\dfrac{2}{\dfrac{2}{3}}=\dfrac{2}{1}\times\dfrac{3}{2}=3$
 
On trouve une même valeur égale à $3.$
 
Ainsi, on a :
$$\left\lbrace\begin{array}{lcl}\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AJ}}}}&=&3\\ \\\dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AJ}}}}&=&3\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl} x_{_{\overrightarrow{AI}}}&=&3\times x_{_{\overrightarrow{AJ}}}\\ \\y_{_{\overrightarrow{AI}}}&=&3\times y_{_{\overrightarrow{AJ}}}\end{array}\right.$$
Ce qui signifie que, $\overrightarrow{AI}=3\overrightarrow{AJ}$
 
Par conséquent, les points $A\;,\ I\ $ et $\ J$ sont alignés.
 
 

Exercice 15

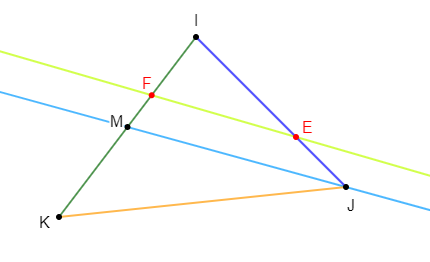
$IJK$ est un triangle. Les points $E\ $ et $\ F$ sont tels que :
$$\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{IJ}\ \text{ et }\ \overrightarrow{IF}=\dfrac{1}{3}\overrightarrow{IK}$$
$M$ est le milieu du segment $[IK].$
 
1) Exprimons $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ en fonction de $\overrightarrow{IJ}\ $ et $\ \overrightarrow{IK}$
 
On a : $\overrightarrow{IF}=\dfrac{1}{3}\overrightarrow{IK}$
 
Alors, introduisons le point $E$ dans le vecteur $\overrightarrow{IF}$ en utilisant la relation de Chasles.
 
On obtient :
$$\overrightarrow{IE}+\overrightarrow{EF}=\dfrac{1}{3}\overrightarrow{IK}$$
Or, on sait que : $\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{IJ}$
 
Donc, en remplaçant $\overrightarrow{IE}$ par $\dfrac{2}{3}\overrightarrow{IJ}$, on trouve :
$$\dfrac{2}{3}\overrightarrow{IJ}+\overrightarrow{EF}=\dfrac{1}{3}\overrightarrow{IK}$$
D'où, $\boxed{\overrightarrow{EF}=-\dfrac{2}{3}\overrightarrow{IJ}+\dfrac{1}{3}\overrightarrow{IK}}$
 
Par ailleurs, en utilisant la relation de Chasles, on introduit le point $M$ dans le vecteur $\overrightarrow{IJ}.$
 
On obtient alors :
$$\overrightarrow{IJ}=\overrightarrow{IM}+\overrightarrow{MJ}$$
Ainsi,
$$-\overrightarrow{MJ}=-\overrightarrow{IJ}+\overrightarrow{IM}$$
Or, on sait que $M$ est le milieu de $[IK].$
 
Ce qui signifie que : $\overrightarrow{IM}=\dfrac{1}{2}\overrightarrow{IK}$
 
Donc, en remplaçant $\overrightarrow{IM}$ par $\dfrac{1}{2}\overrightarrow{IK}$, on trouve :
$$-\overrightarrow{MJ}=-\overrightarrow{IJ}+\dfrac{1}{2}\overrightarrow{IK}$$
D'où, $\boxed{\overrightarrow{JM}=-\overrightarrow{IJ}+\dfrac{1}{2}\overrightarrow{IK}}$
 
2) Montrons que les droites $(EF)\ $ et $\ (JM)$ sont parallèles.
 
En effet, les droites $(EF)\ $ et $\ (JM)$ sont parallèles si, et seulement si, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ sont colinéaires.
 
Or, $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ sont colinéaires si, et seulement si, il existe un nombre réel $k$ non nul, tel que :
$$\overrightarrow{EF}=k\overrightarrow{JM}$$
D'après les résultats de la question $1\;)$, on a :
 
$\begin{array}{rcl}\overrightarrow{EF}&=&-\dfrac{2}{3}\overrightarrow{IJ}+\dfrac{1}{3}\overrightarrow{IK}\\\\&=&\dfrac{2}{3}\left(\underbrace{-\overrightarrow{IJ}+\dfrac{1}{2}\overrightarrow{IK}}_{=\overrightarrow{JM}}\right)\\\\&=&\dfrac{2}{3}\overrightarrow{JM}\end{array}$
 
Ainsi, $\boxed{\overrightarrow{EF}=\dfrac{2}{3}\overrightarrow{JM}}$
 
D'où, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ sont colinéaires.
 
Et par conséquent, les droites $(EF)\ $ et $\ (JM)$ sont parallèles.
 
Autre méthode :
 
En effet, d'après les résultats de la question $1\;)$, on a :
 
$\overrightarrow{EF}=-\dfrac{2}{3}\overrightarrow{IJ}+\dfrac{1}{3}\overrightarrow{IK}$
 
$\overrightarrow{JM}=-\overrightarrow{IJ}+\dfrac{1}{2}\overrightarrow{IK}$
 
Ainsi, dans la base $\left(\overrightarrow{IJ}\;,\ \overrightarrow{IK}\right)$, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ ont pour coordonnées :
$$\overrightarrow{EF}\begin{pmatrix}-\dfrac{2}{3}\\ \\\dfrac{1}{3}\end{pmatrix}\ \text{ et }\ \overrightarrow{JM}\begin{pmatrix}-1\\ \\\dfrac{1}{2}\end{pmatrix}$$
Alors, en appliquant la condition de colinéarité sur ces deux vecteurs, on obtient :
$$-\dfrac{2}{3}\times\dfrac{1}{2}-\dfrac{1}{3}\times(-1)=-\dfrac{1}{3}+\dfrac{1}{3}=0$$
Donc, les coordonnées des vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ vérifient la condition de colinéarité.
 
Ce qui signifie que ces deux vecteurs sont colinéaires.
 
Par conséquent, les droites $(EF)\ $ et $\ (JM)$ sont parallèles.

Nous pouvons aussi utiliser les rapports des coordonnées pour vérifier la colinéarité.
 
Alors, calculons les rapports : $\dfrac{x_{_{\overrightarrow{EF}}}}{x_{_{\overrightarrow{JM}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{EF}}}}{y_{_{\overrightarrow{JM}}}}$
 
On a :
 
$\dfrac{x_{_{\overrightarrow{EF}}}}{x_{_{\overrightarrow{JM}}}}=\dfrac{-\dfrac{2}{3}}{-1}=\dfrac{2}{3}$
 
$\dfrac{y_{_{\overrightarrow{EF}}}}{y_{_{\overrightarrow{JM}}}}=\dfrac{\dfrac{1}{3}}{\dfrac{1}{2}}=\dfrac{1}{3}\times\dfrac{2}{1}=\dfrac{2}{3}$
 
Ainsi,
 
$$\dfrac{x_{_{\overrightarrow{EF}}}}{x_{_{\overrightarrow{JM}}}}=\dfrac{y_{_{\overrightarrow{EF}}}}{y_{_{\overrightarrow{JM}}}}=\dfrac{2}{3}$$
 
D'où, $\boxed{\overrightarrow{EF}=\dfrac{2}{3}\overrightarrow{JM}}$
 
Ce qui signifie que les vecteurs $\overrightarrow{EF}\ $ et $\ \dfrac{2}{3}\overrightarrow{JM}$ sont colinéaires.
 
Par conséquent, les droites $(EF)\ $ et $\ (JM)$ sont parallèles.
 
 

Exercice 16

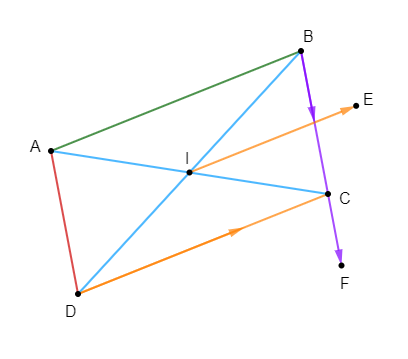
$ABCD$ est un parallélogramme de centre $I.$ Les points $E\ $ et $\ F$ sont tels que :
$$\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{DC}\ \text{ et }\ \overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$$
Exprimons $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$
 
On a : $\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{DC}$
 
En utilisant la relation de Chasles, introduisons le point $A$ dans le vecteur $\overrightarrow{IE}.$
 
On obtient :
$$\overrightarrow{IA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}$$
Comme $ABCD$ est un parallélogramme de centre $I$ alors, $I$ est le milieu de la diagonale $[CA].$
 
D'où, $\overrightarrow{IA}=\dfrac{1}{2}\overrightarrow{CA}$
 
Par ailleurs, en utilisant encore la relation de Chasles, on a :
$$\overrightarrow{CA}=\overrightarrow{CD}+\overrightarrow{DA}$$
Par suite,
$$\overrightarrow{IA}=\dfrac{1}{2}\left(\overrightarrow{CD}+\overrightarrow{DA}\right)$$
Donc, en remplaçant $\overrightarrow{IA}$ par son expression, on obtient :
 
$\begin{array}{rcl}\overrightarrow{IA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}&\Leftrightarrow&\dfrac{1}{2}\left(\overrightarrow{CD}+\overrightarrow{DA}\right)+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}\\\\&\Leftrightarrow&\dfrac{1}{2}\overrightarrow{CD}+\dfrac{1}{2}\overrightarrow{DA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}-\dfrac{1}{2}\overrightarrow{CD}-\dfrac{1}{2}\overrightarrow{DA}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}+\dfrac{1}{2}\overrightarrow{DC}+\dfrac{1}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{7}{6}\overrightarrow{DC}+\dfrac{1}{2}\overrightarrow{AD}\end{array}$
 
Comme $ABCD$ est un parallélogramme alors,
$$\overrightarrow{DC}=\overrightarrow{AB}$$
D'où, en remplaçant $\overrightarrow{DC}$ par $\overrightarrow{AB}$, on trouve : $\boxed{\overrightarrow{AE}=\dfrac{7}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}}$
 
Soit : $\overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$
 
Alors, introduisons le point $A$ dans le vecteur $\overrightarrow{BF}$, par la relation de Chasles.
 
On obtient :
$$\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{BC}$$
Comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{BC}=\overrightarrow{AD}$$
Ainsi, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{AD}$, on trouve :
 
$\begin{array}{rcl}\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{BC}&\Leftrightarrow&\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AF}=-\overrightarrow{BA}+\dfrac{3}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}\end{array}$
 
D'où, $\boxed{\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}}$
 
 

Exercice 17

$ABC$ est un triangle,$\alpha$ un nombre réel. On considère les points $P\;,\ Q\ $ et $\ R$ définis par : $$\overrightarrow{AP}=\alpha\overrightarrow{AB}\;,\quad \overrightarrow{CQ}=\alpha\overrightarrow{CA}\;,\quad \overrightarrow{CR}=\alpha\overrightarrow{BC}$$

1) Exprimons $\overrightarrow{PQ}\ $ et $\ \overrightarrow{PR}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$

Soit : $\overrightarrow{CQ}=\alpha\overrightarrow{CA}$

Alors, dans le vecteur $\overrightarrow{CQ}$ introduisons le point $P$ en utilisant la relation de Chasles.

On obtient :
$$\overrightarrow{CP}+\overrightarrow{PQ}=\alpha\overrightarrow{CA}$$
En utilisant le même procédé, introduisons le point $A$ dans le vecteur $\overrightarrow{CP}.$

Cela donne alors :
$$\overrightarrow{CA}+\overrightarrow{AP}+\overrightarrow{PQ}=\alpha\overrightarrow{CA}$$
Or, on sait que : $\overrightarrow{AP}=\alpha\overrightarrow{AB}$

Donc, en remplaçant $\overrightarrow{AP}$ par $\alpha\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :

$\begin{array}{rcl}\overrightarrow{CA}+\overrightarrow{AP}+\overrightarrow{PQ}=\alpha\overrightarrow{CA}&\Leftrightarrow&\overrightarrow{CA}+\alpha\overrightarrow{AB}+\overrightarrow{PQ}=\alpha\overrightarrow{CA}\\\\&\Leftrightarrow&\overrightarrow{PQ}=-\alpha\overrightarrow{AB}-\overrightarrow{CA}+\alpha\overrightarrow{CA}\\\\&\Leftrightarrow&\overrightarrow{PQ}=-\alpha\overrightarrow{AB}+\overrightarrow{AC}-\alpha\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{PQ}=-\alpha\overrightarrow{AB}+(1-\alpha)\overrightarrow{AC}\end{array}$

D'où, $\boxed{\overrightarrow{PQ}=-\alpha\overrightarrow{AB}+(1-\alpha)\overrightarrow{AC}}$

Soit : $\overrightarrow{CR}=\alpha\overrightarrow{BC}$

Alors, de la même manière, utilisons la relation de Chasles pour introduire le point $P$ dans le vecteur $\overrightarrow{CR}.$

On obtient :
$$\overrightarrow{CP}+\overrightarrow{PR}=\alpha\overrightarrow{BC}$$
En utilisant le même procédé, introduisons le point $A$ dans le vecteur $\overrightarrow{CP}$ puis, dans le vecteur $\overrightarrow{BC}.$

Ce qui donne :
$$\overrightarrow{CA}+\overrightarrow{AP}+\overrightarrow{PR}=\alpha\left(\overrightarrow{BA}+\overrightarrow{AC}\right)$$
Par ailleurs, on sait que : $\overrightarrow{AP}=\alpha\overrightarrow{AB}$

Alors, en remplaçant $\overrightarrow{AP}$ par $\alpha\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :

$\begin{array}{rcl}\overrightarrow{CA}+\overrightarrow{AP}+\overrightarrow{PR}=\alpha\left(\overrightarrow{BA}+\overrightarrow{AC}\right)&\Leftrightarrow&\overrightarrow{CA}+\alpha\overrightarrow{AB}+\overrightarrow{PR}=\alpha\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\\\\&\Leftrightarrow&\overrightarrow{PR}=-\alpha\overrightarrow{AB}-\overrightarrow{CA}+\alpha\overrightarrow{BA}+\alpha\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{PR}=-\alpha\overrightarrow{AB}-\alpha\overrightarrow{AB}+\overrightarrow{AC}+\alpha\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{PR}=-2\alpha\overrightarrow{AB}+(1+\alpha)\overrightarrow{AC}\end{array}$

Par conséquent, $\boxed{\overrightarrow{PR}=-2\alpha\overrightarrow{AB}+(1+\alpha)\overrightarrow{AC}}$

2) Vérifions s'il existe des valeurs de $\alpha$ pour lesquels les points $P\;,\ Q\ $ et $\ R$ sont alignés.

En effet, d'après les résultats de la question $1\;)$, on a :

$\overrightarrow{PQ}=-\alpha\overrightarrow{AB}+(1-\alpha)\overrightarrow{AC}$

$\overrightarrow{PR}=-2\alpha\overrightarrow{AB}+(1+\alpha)\overrightarrow{AC}$

Donc, dans la base $\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$, les vecteurs $\overrightarrow{PQ}\ $ et $\ \overrightarrow{PR}$ ont pour coordonnées :
$$\overrightarrow{PQ}\begin{pmatrix}-\alpha\\ \\(1-\alpha)\end{pmatrix}\ \text{ et }\ \overrightarrow{PR}\begin{pmatrix}-2\alpha\\ \\(1+\alpha)\end{pmatrix}$$
Or, on sait que les points $P\;,\ Q\ $ et $\ R$ sont alignés si, et seulement si, les coordonnées des vecteurs $\overrightarrow{PQ}\ $ et $\ \overrightarrow{PR}$ vérifient :
$$\dfrac{x_{_{\overrightarrow{PQ}}}}{x_{_{\overrightarrow{PR}}}}=\dfrac{y_{_{\overrightarrow{PQ}}}}{y_{_{\overrightarrow{PR}}}}=\text{Constante}$$
Soit alors :

$\begin{array}{rcl}\dfrac{x_{_{\overrightarrow{PQ}}}}{x_{_{\overrightarrow{PR}}}}=\dfrac{y_{_{\overrightarrow{PQ}}}}{y_{_{\overrightarrow{PR}}}}&\Leftrightarrow&\dfrac{-\alpha}{-2\alpha}=\dfrac{(1-\alpha)}{(1+\alpha)}\\\\&\Leftrightarrow&\dfrac{1}{2}=\dfrac{(1-\alpha)}{(1+\alpha)}\\\\&\Leftrightarrow&1(1+\alpha)=2(1-\alpha)\\\\&\Leftrightarrow&1+\alpha=2-2\alpha\\\\&\Leftrightarrow&\alpha+2\alpha=2-1\\\\&\Leftrightarrow&3\alpha=1\\\\&\Leftrightarrow&\alpha=\dfrac{1}{3}\end{array}$

D'où, $\boxed{\alpha=\dfrac{1}{3}}$

Ainsi, les points $P\;,\ Q\ $ et $\ R$ sont alignés lorsque $\alpha=\dfrac{1}{3}.$

Exercice 18

$A\;,\ B\ $ et $\ C$ sont trois points non alignés. Les points $D\;,\ E\ $ et $\ F$ sont définis par les égalités de vecteurs suivants :
$$\overrightarrow{AD}=3\overrightarrow{AB}\;,\quad \overrightarrow{AE}=\dfrac{3}{2}\overrightarrow{AC}\;,\quad \overrightarrow{BF}=2\overrightarrow{BC}$$
1) Exprimons $\overrightarrow{DE}\ $ et $\ \overrightarrow{DF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$

Soit : $\overrightarrow{AE}=\dfrac{3}{2}\overrightarrow{AC}$

Alors, en introduisant le point $D$ dans le vecteur $\overrightarrow{AE}$, par la relation de Chasles, on obtient :
$$\overrightarrow{AD}+\overrightarrow{DE}=\dfrac{3}{2}\overrightarrow{AC}$$
Or, on sait que : $\overrightarrow{AD}=3\overrightarrow{AB}$

Donc, en remplaçant $\overrightarrow{AD}$ par $3\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :

$\begin{array}{rcl}\overrightarrow{AD}+\overrightarrow{DE}=\dfrac{3}{2}\overrightarrow{AC}&\Leftrightarrow&3\overrightarrow{AB}+\overrightarrow{DE}=\dfrac{3}{2}\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{DE}=-3\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\end{array}$

D'où, $\boxed{\overrightarrow{DE}=-3\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}}$

Soit : $\overrightarrow{BF}=2\overrightarrow{BC}$

Alors, de la même manière, en utilisant la relation de Chasles pour introduire le point $D$ dans le vecteur $\overrightarrow{BF}$, on obtient :
$$\overrightarrow{BD}+\overrightarrow{DF}=2\overrightarrow{BC}$$
Ensuite, utilisons le même procédé pour introduire le point $A$ dans le vecteur $\overrightarrow{BD}$ puis, dans le vecteur $\overrightarrow{BC}.$

Cela donne alors :
$$\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DF}=2\left(\overrightarrow{BA}+\overrightarrow{AC}\right)$$
Comme $\overrightarrow{AD}=3\overrightarrow{AB}$ alors, en remplaçant $\overrightarrow{AD}$ par $3\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :

$\begin{array}{rcl}\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DF}=2\left(\overrightarrow{BA}+\overrightarrow{AC}\right)&\Leftrightarrow&\overrightarrow{BA}+3\overrightarrow{AB}+\overrightarrow{DF}=2\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\\\\&\Leftrightarrow&\overrightarrow{DF}=-3\overrightarrow{AB}-\overrightarrow{BA}+2\overrightarrow{BA}+2\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{DF}=-3\overrightarrow{AB}+\overrightarrow{AB}-2\overrightarrow{AB}+2\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{DF}=-4\overrightarrow{AB}+2\overrightarrow{AC}\end{array}$

Par conséquent, $\boxed{\overrightarrow{DF}=-4\overrightarrow{AB}+2\overrightarrow{AC}}$

2) Montrons que les points $D\;,\ E\ $ et $\ F$ sont alignés.

En effet, les points $D\;,\ E\ $ et $\ F$ sont alignés si, et seulement si, il existe un nombre réel $k$ non nul tel que :
$$\overrightarrow{DE}=k\overrightarrow{DF}$$
D'après les résultats de la question $1\;)$, on a :

$\overrightarrow{DE}=-3\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}$

$\overrightarrow{DF}=-4\overrightarrow{AB}+2\overrightarrow{AC}$

Ainsi, dans la base $\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$, les coordonnées des vecteurs $\overrightarrow{DE}\ $ et $\ \overrightarrow{DF}$ sont données par :
$$\overrightarrow{DE}\begin{pmatrix}-3\\ \\\dfrac{3}{2}\end{pmatrix}\ \text{ et }\ \overrightarrow{DF}\begin{pmatrix}-4\\ \\2\end{pmatrix}$$
Calculons alors les rapports : $\dfrac{x_{_{\overrightarrow{DE}}}}{x_{_{\overrightarrow{DF}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{DE}}}}{y_{_{\overrightarrow{DF}}}}$

On a :

$\dfrac{x_{_{\overrightarrow{DE}}}}{x_{_{\overrightarrow{DF}}}}=\dfrac{-3}{-4}=\dfrac{3}{4}$

$\dfrac{y_{_{\overrightarrow{DE}}}}{y_{_{\overrightarrow{DF}}}}=\dfrac{\dfrac{3}{2}}{2}=\dfrac{3}{2}\times\dfrac{1}{2}=\dfrac{3}{4}$

On constate que l'on trouve une même valeur égale à $\dfrac{3}{4}.$

Ainsi, on peut écrire :
$$\left\lbrace\begin{array}{lcl}\dfrac{x_{_{\overrightarrow{DE}}}}{x_{_{\overrightarrow{DF}}}}&=&\dfrac{3}{4}\\ \\\dfrac{y_{_{\overrightarrow{DE}}}}{y_{_{\overrightarrow{DF}}}}&=&\dfrac{3}{4}\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl} x_{_{\overrightarrow{DE}}}&=&\dfrac{3}{4}\times x_{_{\overrightarrow{DF}}}\\ \\y_{_{\overrightarrow{DE}}}&=&\dfrac{3}{4}\times y_{_{\overrightarrow{DF}}}\end{array}\right.$$
Par conséquent, $\boxed{\overrightarrow{DE}=\dfrac{3}{4}\overrightarrow{DF}}$

Ce qui montre que les points $D\;,\ E\ $ et $\ F$ sont alignés.


 

 

Exercice 19

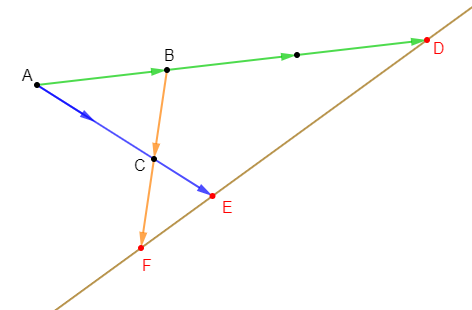
Le segment $[AB]$ est divisé en $6$ parties de même longueur. Complétons les relations suivantes par la lettre ou le nombre qui convient.
 
 
1) $EC=2EF$
 
2) $CE=EG$
 
3) $AB=AB$
 
4) $CE=\dfrac{1}{3}AB$
 
5) $AD=BF$
 
6) $DE=\dfrac{1}{2}BF$
 

Exercice 20

$ABCD$ est un parallélogramme. Les points $E\ $ et $\ F$ sont tels que :
$$\overrightarrow{DE}=\dfrac{2}{3}\overrightarrow{DC}\ \text{ et }\ \overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$$
1) Exprimons $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$
 
Soit : $\overrightarrow{DE}=\dfrac{2}{3}\overrightarrow{DC}$
 
Alors, par la relation de Chasles, en introduisant le point $A$ dans le vecteur $\overrightarrow{DE}$, on obtient :
$$\overrightarrow{DA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}$$
Par ailleurs, comme $ABCD$ est un parallélogramme alors,
$$\overrightarrow{DC}=\overrightarrow{AB}$$
Ainsi, en remplaçant $\overrightarrow{DC}$ par $\overrightarrow{AB}$, on trouve : 
 
$\begin{array}{rcl}\overrightarrow{DA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}&\Leftrightarrow&\overrightarrow{DA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}-\overrightarrow{DA}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}\end{array}$
 
D'où, $\boxed{\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}}$
 
Soit : $\overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$
 
Alors, introduisons le point $A$ dans le vecteur $\overrightarrow{BF}$, par la relation de Chasles.
 
On obtient :
$$\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{BC}$$
Comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{BC}=\overrightarrow{AD}$$
Ainsi, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{AD}$, on trouve :
 
$\begin{array}{rcl}\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{BC}&\Leftrightarrow&\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AF}=-\overrightarrow{BA}+\dfrac{3}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}\end{array}$
 
D'où, $\boxed{\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}}$
 
2) Montrons que les points $A\;,\ E\ $ et $\ F$ sont alignés.
 
En effet, les points $A\;,\ E\ $ et $\ F$ sont alignés si, et seulement si, il existe un nombre réel $k$ non nul tel que :
$$\overrightarrow{AE}=k\overrightarrow{AF}$$
D'après les résultats de la question $1\;)$, on a :
 
$\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}$
 
$\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}$
 
Ainsi, dans le repère $\left(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AD}\right)$, les vecteurs $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ ont pour coordonnées :
$$\overrightarrow{AE}\begin{pmatrix}\dfrac{2}{3}\\ \\1\end{pmatrix}\ \text{ et }\ \overrightarrow{AF}\begin{pmatrix}1\\ \\\dfrac{3}{2}\end{pmatrix}$$
Alors, en calculant alors les rapports : $\dfrac{x_{_{\overrightarrow{AE}}}}{x_{_{\overrightarrow{AF}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{AE}}}}{y_{_{\overrightarrow{AF}}}}$, on trouve :
 
$\dfrac{x_{_{\overrightarrow{AE}}}}{x_{_{\overrightarrow{AF}}}}=\dfrac{\dfrac{2}{3}}{1}=\dfrac{2}{3}$
 
$\dfrac{y_{_{\overrightarrow{AE}}}}{y_{_{\overrightarrow{AF}}}}=\dfrac{1}{\dfrac{3}{2}}=1\times\dfrac{2}{3}=\dfrac{2}{3}$
 
Ainsi, nous obtenons une même valeur égale à $\dfrac{2}{3}.$
 
Par suite, on peut écrire :
$$\left\lbrace\begin{array}{lcl}\dfrac{x_{_{\overrightarrow{AE}}}}{x_{_{\overrightarrow{AF}}}}&=&\dfrac{2}{3}\\ \\\dfrac{y_{_{\overrightarrow{AE}}}}{y_{_{\overrightarrow{AF}}}}&=&\dfrac{2}{3}\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl} x_{_{\overrightarrow{AE}}}&=&\dfrac{2}{3}\times x_{_{\overrightarrow{AF}}}\\ \\y_{_{\overrightarrow{AE}}}&=&\dfrac{2}{3}\times y_{_{\overrightarrow{AF}}}\end{array}\right.$$
Par conséquent, $\boxed{\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AF}}$
 
Ce qui montre que les points $A\;,\ E\ $ et $\ F$ sont alignés.
 
Autre méthode :
 
On a :
 
$\begin{array}{rcl}\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\left(\underbrace{\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}}_{=\overrightarrow{AF}}\right)\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AF}\end{array}$
 
D'où, $\boxed{\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AF}}$
 
Par conséquent, les points $A\;,\ E\ $ et $\ F$ sont alignés.

 
 

Exercice 21

Soit $ABC$ un triangle quelconque.
 
1) Construisons les points $D\ $ et $\ E$ tels que $\overrightarrow{AD}=\overrightarrow{BC}\;,\quad\overrightarrow{CE}=2\overrightarrow{BA}$
 
2) Démontrons que $D$ est le milieu de $[CE]$
 
En effet, on a :
$$\overrightarrow{CE}=2\overrightarrow{BA}$$
Par ailleurs, on sait que :
$$\overrightarrow{AD}=\overrightarrow{BC}$$
Ce qui signifie que $ADCB$ est un parallélogramme.
 
Par conséquent,
$$\overrightarrow{BA}=\overrightarrow{CD}$$
Ainsi, dans l'expression de $\overrightarrow{CE}$, en remplaçant $\overrightarrow{BA}$ par $\overrightarrow{CD}$, on obtient :
$$\boxed{\overrightarrow{CE}=2\overrightarrow{CD}}$$
Ce qui démontre que $D$ est le milieu de $[CE]$

 
 

Exercice 22

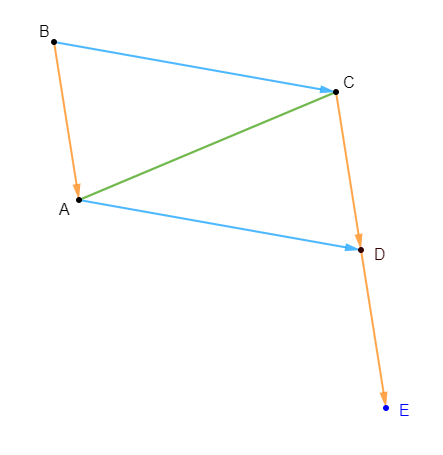
Soit $ABC$ un triangle. Construisons les points $M\ $ et $\ N$ tels que : $$\left\lbrace\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}&=&\overrightarrow{AB} \\\\ \overrightarrow{AN}-\overrightarrow{AM}&=&\overrightarrow{AC}\end{array}\right.$$
 
Pour cela, nous allons d'abord exprimer les vecteurs $\overrightarrow{AN}\ $ et $\ \overrightarrow{AM}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$
 
En effet, résolvons ce système en additionnant membre à membre les deux égalités.
 
On obtient :
 
$\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}+\overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}&\Leftrightarrow&2\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{AN}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{2}\end{array}$
 
D'où, $\boxed{\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}}$
 
En remplaçant $\overrightarrow{AN}$ par son expression, dans la première égalité, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}=\overrightarrow{AB}&\Leftrightarrow&\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}+\overrightarrow{AM}=\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{AM}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\end{array}$
 
D'où, $\boxed{\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}}$
 
 
 

Exercice 23

Construisons trois vecteurs $\vec{u}\;,\ \vec{v}\ $ et $\ \vec{w}$ tels que :
$$\left\lbrace\begin{array}{rcl}\vec{u}+\vec{v}-2\vec{w}&=&\vec{0} \\ \vec{u}-\vec{v}+\vec{w}&=&\vec{0}\end{array}\right.$$
Pour cela, nous allons d'abord exprimer $\vec{u}\ $ et $\ \vec{v}$ en fonction de $\vec{w}.$
 
En additionnant membre à membre les deux égalités du système, on obtient :
 
$\begin{array}{rcl}\vec{u}+\vec{v}-2\vec{w}+\vec{u}-\vec{v}+\vec{w}=\vec{0}+\vec{0}&\Leftrightarrow&2\vec{u}-\vec{w}=\vec{0}\\\\&\Leftrightarrow&2\vec{u}=\vec{w}\\\\&\Leftrightarrow&\vec{u}=\dfrac{1}{2}\vec{w}\end{array}$
 
Donc, $\boxed{\vec{u}=\dfrac{1}{2}\vec{w}}$
 
En remplaçant $\vec{u}$ par son expression, dans la première égalité, on obtient :
 
$\begin{array}{rcl}\vec{u}+\vec{v}-2\vec{w}=\vec{0}&\Leftrightarrow&\dfrac{1}{2}\vec{w}+\vec{v}-2\vec{w}=\vec{0}\\\\&\Leftrightarrow&\vec{v}-\dfrac{3}{2}\vec{w}=\vec{0}\\\\&\Leftrightarrow&\vec{v}=\dfrac{3}{2}\vec{w}\end{array}$
 
D'où, $\boxed{\vec{v}=\dfrac{3}{2}\vec{w}}$
 
Ainsi, on place d'abord $\vec{w}$ puis, on trace les vecteurs $\vec{u}\ $ et $\ \vec{v}.$
 
 
Démontrons que $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires au vecteur $\vec{w}.$ 
 
En effet, d'après les résultats de la question $1\;)$, on a :
$$\vec{u}=\dfrac{1}{2}\vec{w}\quad\text{et}\quad\vec{v}=\dfrac{3}{2}\vec{w}$$
Par conséquent, $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires au vecteur $\vec{w}.$

Exercice 24

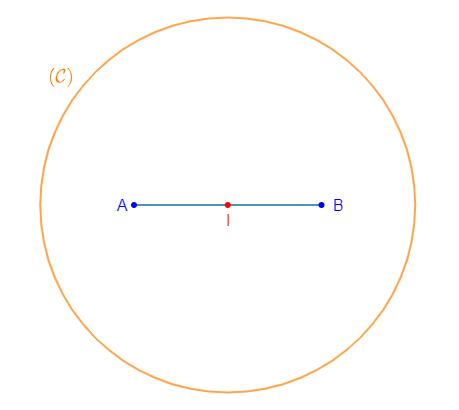
Soit $A\ $ et $\ B$ deux points distincts du plan, $I$ milieu de $[AB]$
 
1) Démontrons que pour tout point $M$ du plan :
$$\overrightarrow{AM}+\overrightarrow{BM}=2\overrightarrow{IM}$$
En effet, par la relation de Chasles, en introduisant le point $I$ dans les vecteurs $\overrightarrow{AM}\ $ et $\ \overrightarrow{BM}$, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AM}+\overrightarrow{BM}&=&\overrightarrow{AI}+\overrightarrow{IM}+\overrightarrow{BI}+\overrightarrow{IM}\\\\&=&2\overrightarrow{IM}+\underbrace{\overrightarrow{AI}+\overrightarrow{BI}}_{=\vec{0}}\end{array}$
 
Or, on sait que $I$ est le milieu de $[AB].$
 
Donc, $\overrightarrow{AI}+\overrightarrow{BI}=\vec{0}$
 
D'où, $\boxed{\overrightarrow{AM}+\overrightarrow{BM}=2\overrightarrow{IM}}$
 
2) Déterminons et construisons l'ensemble $(\mathcal{C})$ des points $M$ du plan tels que :
$$||\overrightarrow{AM}+\overrightarrow{BM}||=2AB$$
En effet, d'après le résultat de la question $1\;)$, on a :
$$\overrightarrow{AM}+\overrightarrow{BM}=2\overrightarrow{IM}$$
Donc, en remplaçant $\overrightarrow{AM}+\overrightarrow{BM}$ par $2\overrightarrow{IM}$, on obtient :
 
$\begin{array}{rcl}||\overrightarrow{AM}+\overrightarrow{BM}||=2AB&\Leftrightarrow&||2\overrightarrow{IM}||=2AB\\\\&\Leftrightarrow&2||\overrightarrow{IM}||=2AB\\\\&\Leftrightarrow&||\overrightarrow{IM}||=\dfrac{2AB}{2}\\\\&\Leftrightarrow&||\overrightarrow{IM}||=AB\end{array}$
 
D'où, $\boxed{||\overrightarrow{IM}||=AB}$
 
Alors, $(\mathcal{C})$ est l'ensemble des points $M$ du plan équidistants à un même point $I$ et à une distance égale à la longueur $AB.$
 
C'est donc le cercle de centre $I$ et de rayon $AB.$
 

 

Exercice 25

Soit un triangle $DIM$ et soit $A$ le milieu de $[DM].$
 
a) Construisons les points $T\ $ et $\ H$ tels que :
$$\overrightarrow{DT}=4\overrightarrow{DI}\quad\text{ et }\quad\overrightarrow{IH}=3\overrightarrow{IM}$$
b) Démontrons que $(TH)//(IA)$
 
En effet, pour démontrer que les droites $(TH)\ $ et $\ (IA)$ sont parallèles il suffit de montrer que les vecteurs $\overrightarrow{TH}\ $ et $\ \overrightarrow{IA}$ sont colinéaires.
 
On a : $\overrightarrow{IH}=3\overrightarrow{IM}$
 
Donc, par la relation de Chasles, introduisons le point $T$ dans le vecteur $\overrightarrow{IH}.$
 
On obtient :
$$\overrightarrow{IT}+\overrightarrow{TH}=3\overrightarrow{IM}$$
Utilisons encore la relation de Chasles pour introduire le point $D$ dans le vecteur $\overrightarrow{IT}.$
 
Ce qui donne :
$$\overrightarrow{ID}+\overrightarrow{DT}+\overrightarrow{TH}=3\overrightarrow{IM}$$
Or, on sait que : $\overrightarrow{DT}=4\overrightarrow{DI}$
 
Donc, en remplaçant $\overrightarrow{DT}$ par $4\overrightarrow{DI}$, on trouve :
 
$\begin{array}{rcl}\overrightarrow{ID}+\overrightarrow{DT}+\overrightarrow{TH}=3\overrightarrow{IM}&\Leftrightarrow&\overrightarrow{ID}+4\overrightarrow{DI}+\overrightarrow{TH}=3\overrightarrow{IM}\\\\&\Leftrightarrow&\overrightarrow{TH}=3\overrightarrow{IM}-\overrightarrow{ID}-4\overrightarrow{DI}\\\\&\Leftrightarrow&\overrightarrow{TH}=3\overrightarrow{IM}-\overrightarrow{ID}+4\overrightarrow{ID}\\\\&\Leftrightarrow&\overrightarrow{TH}=3\overrightarrow{IM}+3\overrightarrow{ID}\\\\&\Leftrightarrow&\overrightarrow{TH}=3\left(\overrightarrow{IM}+\overrightarrow{ID}\right)\end{array}$
 
Ainsi, en utilisant encore la relation de Chasles, introduisons le point $A$ dans les vecteurs $\overrightarrow{IM}\ $ et $\ \overrightarrow{ID}.$
 
On obtient :
 
$\begin{array}{rcl}\overrightarrow{TH}&=&3\left(\overrightarrow{IM}+\overrightarrow{ID}\right)\\\\&=&3\left(\overrightarrow{IA}+\overrightarrow{AM}+\overrightarrow{IA}+\overrightarrow{AD}\right)\\\\&=&3\left(2\overrightarrow{IA}+\underbrace{\overrightarrow{AM}+\overrightarrow{AD}}_{=\vec{0}}\right)\end{array}$
 
Par ailleurs, on sait que $A$ est le milieu de $[DM].$
 
Ce qui signifie que :
$$\overrightarrow{AM}+\overrightarrow{AD}=\vec{0}$$
D'où, $\boxed{\overrightarrow{TH}=6\overrightarrow{IA}}$
 
Ce qui montre que les vecteurs $\overrightarrow{TH}\ $ et $\ \overrightarrow{IA}$ sont colinéaires.
 
Par conséquent, les droites $(TH)\ $ et $\ (IA)$ sont parallèles.
 

 

Exercice 26

Soit $ABC$ un triangle quelconque.
 
1) a) Montrons que l'égalité $\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}$ équivaut à l'égalité $\overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}.$
 
En effet, soit l'égalité :
$$\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}$$
Alors, par la relation de Chasles, introduisons le point $A$ dans les vecteurs $\overrightarrow{DB}\ $ et $\ \overrightarrow{DC}.$
 
On obtient :
 
$\begin{array}{rcl}\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}&\Leftrightarrow&\overrightarrow{DA}-3\left(\overrightarrow{DA}+\overrightarrow{AB}\right)+\left(\overrightarrow{DA}+\overrightarrow{AC}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{DA}-3\overrightarrow{DA}-3\overrightarrow{AB}+\overrightarrow{DA}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&-\overrightarrow{DA}-3\overrightarrow{AB}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AD}-3\overrightarrow{AB}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}\end{array}$
 
D'où, $\boxed{\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}\quad \Leftrightarrow\quad \overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}}$
 
Construisons le point $D.$
 
Pour construire le point $D$, on utilise la relation :
$$\overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}$$
b) Montrons que $\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}=-\overrightarrow{MD}$ quelque soit le point $M.$
 
En effet, par la relation de Chasles, en introduisant le point $D$ dans les vecteurs $\overrightarrow{MA}\;,\ \overrightarrow{MB}\ $ et $\ \overrightarrow{MC}$, on obtient :
 
$\begin{array}{rcl}\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}&=&\left(\overrightarrow{MD}+\overrightarrow{DA}\right)-3\left(\overrightarrow{MD}+\overrightarrow{DB}\right)+\left(\overrightarrow{MD}+\overrightarrow{DC}\right)\\\\&=&\overrightarrow{MD}+\overrightarrow{DA}-3\overrightarrow{MD}-3\overrightarrow{DB}+\overrightarrow{MD}+\overrightarrow{DC}\\\\&=&-\overrightarrow{MD}+\underbrace{\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}}_{=\vec{0}}\end{array}$
 
Or, d'après la question $1\;a\;)$, on a :
$$\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}$$
D'où, $\boxed{\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}=-\overrightarrow{MD}}$
 
c) Montrons que $\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{BD}$
 
D'après le résultat de la question $1\;b\;)$, on a :
$$\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}=-\overrightarrow{MD}$$
quelque soit le point $M.$
 
Donc, en posant $M=B$ ou en remplaçant $M$ par $B$ dans cette relation, on obtient :
$$\overrightarrow{BA}-3\overrightarrow{BB}+\overrightarrow{BC}=-\overrightarrow{BD}$$
D'où, $\boxed{\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{BD}}$
 
2) Soit $M$ un point quelconque, on pose :
$$\vec{V}=\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}$$
Montrons que :
$$\vec{V}=\overrightarrow{BA}+\overrightarrow{BC}$$
En effet, soit : $\vec{V}=\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}$
 
Alors, par la relation de Chasles, introduisons le point $B$ dans les vecteurs $ \overrightarrow{MA}\ $ et $\ \overrightarrow{MC}.$
 
On obtient :
 
$\begin{array}{rcl}\vec{V}&=&\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}\\\\&=&\left(\overrightarrow{MB}+\overrightarrow{BA}\right)-2\overrightarrow{MB}+\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\\\\&=&\overrightarrow{MB}+\overrightarrow{BA}-2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{BC}\\\\&=&\overrightarrow{BA}+\overrightarrow{BC}\end{array}$
 
Ainsi, $\boxed{\vec{V}=\overrightarrow{BA}+\overrightarrow{BC}}$
 
Plaçons le point $E$ défini par :
$$\vec{V}=\overrightarrow{AE}$$
Cela revient donc à placer le point $E$ tel que :
$$\overrightarrow{AE}=\overrightarrow{BA}+\overrightarrow{BC}$$
3) Montrons que les droites $(BD)\ $ et $\ (AE)$ sont parallèles.
 
Pour cela, il suffit de montrer que $\overrightarrow{AE}\ $ et $\ \overrightarrow{BD}$ sont colinéaires.
 
En effet, d'après le résultat de la question $1\;c\;)$, on a :
$$\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{BD}$$
Par ailleurs, d'après la question $2\;)$, on a :
$$\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AE}$$
Ainsi, $\boxed{\overrightarrow{AE}=-\overrightarrow{BD}}$
 
Ce qui signifie que les vecteurs $\overrightarrow{AE}\ $ et $\ \overrightarrow{BD}$ sont colinéaires.
 
Par conséquent, les droites $(BD)\ $ et $\ (AE)$ sont parallèles.

 

 

Exercice 27

Soit $ABC$ un triangle
 
1) Construisons les points $M\ $ et $\ N$ tels que :
$$\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AB}\quad\text{ et }\quad\overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AC}$$
2) Démontrons que $(MN)//(BC)$
 
En effet, on a : $M\;,\ A\ $ et $\ B$ trois points alignés d'une part, $N\;,\ A\ $ et $\ C$ trois points alignés d'autre part, dans le même ordre.
 
Calculons alors les rapports :
$$\dfrac{\left\|\overrightarrow{AM}\right\|}{\left\|\overrightarrow{AB}\right\|}\quad\text{ et }\quad\dfrac{\left\|\overrightarrow{AN}\right\|}{\left\|\overrightarrow{AC}\right\|}$$
On a :
 
$\dfrac{\left\|\overrightarrow{AM}\right\|}{\left\|\overrightarrow{AB}\right\|}=\dfrac{\left\|-\dfrac{2}{3}\overrightarrow{AB}\right\|}{\left\|\overrightarrow{AB}\right\|}=\left|-\dfrac{2}{3}\right|\dfrac{\left\|\overrightarrow{AB}\right\|}{\left\|\overrightarrow{AB}\right\|}=\dfrac{2}{3}$
 
$\dfrac{\left\|\overrightarrow{AN}\right\|}{\left\|\overrightarrow{AC}\right\|}=\dfrac{\left\|-\dfrac{2}{3}\overrightarrow{AC}\right\|}{\left\|\overrightarrow{AC}\right\|}=\left|-\dfrac{2}{3}\right|\dfrac{\left\|\overrightarrow{AC}\right\|}{\left\|\overrightarrow{AC}\right\|}=\dfrac{2}{3}$
 
Ainsi,
$$\dfrac{\left\|\overrightarrow{AM}\right\|}{\left\|\overrightarrow{AB}\right\|}=\dfrac{\left\|\overrightarrow{AN}\right\|}{\left\|\overrightarrow{AC}\right\|}=\dfrac{2}{3}$$
Par conséquent, d'après la réciproque du théorème de Thalès, les droites $(MN)\ $ et $\ (BC)$ sont parallèles.
 
Autre méthode :
 
En effet, pour montrer que les droites $(MN)\ $ et $\ (BC)$ sont parallèles, il suffit de montrer que les vecteurs $\overrightarrow{MN}\ $ et $\ \overrightarrow{BC}$ sont colinéaires.
 
D'après la question $1\;)$, on a :
 
$\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AB}$
 
$\overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AC}$
 
Donc, en faisant la différence membre à membre de ces deux relations, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AN}-\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AC}-\left(-\dfrac{2}{3}\overrightarrow{AB}\right)&\Leftrightarrow&\overrightarrow{AN}+\overrightarrow{MA}=-\dfrac{2}{3}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{AN}+\overrightarrow{MA}=-\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\\\\&\Leftrightarrow&\overrightarrow{AN}+\overrightarrow{MA}=-\dfrac{2}{3}\left(\overrightarrow{AC}+\overrightarrow{BA}\right)\\\\&\Leftrightarrow&\overrightarrow{MA}+\overrightarrow{AN}=-\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\end{array}$
 
En appliquant la relation de Chasles, on trouve :
$$\boxed{\overrightarrow{MN}=-\dfrac{2}{3}\overrightarrow{BC}}$$
Ce qui montre que les vecteurs $\overrightarrow{MN}\ $ et $\ \overrightarrow{BC}$ sont colinéaires.
 
Par conséquent, les droites $(MN)\ $ et $\ (BC)$ sont parallèles.
 
3) Soient $S\ $ et $\ T$ les milieux respectifs de $[BC]\ $ et $\ [MN].$
 
Démontrons que les points $A\;,\ S\ $ et $\ T$ sont alignés.
 
Soit :
 
$\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AB}$
 
$\overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AC}$
 
Alors, en additionnant membre à membre ces deux relations, on obtient :
 
$$\overrightarrow{AN}+\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AC}-\dfrac{2}{3}\overrightarrow{AB}$$
 
Ensuite, par la relation de Chasles, introduisons le point $T$ dans les vecteurs $\overrightarrow{AN}\ $ et $\ \overrightarrow{AM}$ puis, le point $S$ dans les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{AB}.$
 
On obtient :
 
$\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AC}-\dfrac{2}{3}\overrightarrow{AB}&\Leftrightarrow&\left(\overrightarrow{AT}+\overrightarrow{TN}\right)+\left(\overrightarrow{AT}+\overrightarrow{TM}\right)=-\dfrac{2}{3}\left(\overrightarrow{AS}+\overrightarrow{SC}\right)-\dfrac{2}{3}\left(\overrightarrow{AS}+\overrightarrow{SB}\right)\\\\&\Leftrightarrow&\overrightarrow{AT}+\overrightarrow{TN}+\overrightarrow{AT}+\overrightarrow{TM}=-\dfrac{2}{3}\overrightarrow{AS}-\dfrac{2}{3}\overrightarrow{SC}-\dfrac{2}{3}\overrightarrow{AS}-\dfrac{2}{3}\overrightarrow{SB}\\\\&\Leftrightarrow&2\overrightarrow{AT}+\underbrace{\overrightarrow{TN}+\overrightarrow{TM}}_{=\vec{0}}=-\dfrac{4}{3}\overrightarrow{AS}-\dfrac{2}{3}\left(\underbrace{\overrightarrow{SC}+\overrightarrow{SB}}_{=\vec{0}}\right)\end{array}$
 
Or, $T$ est milieu de $[MN]\ $ et $\ S$ milieu de $[BC].$
 
Donc, cela signifie :
$$\overrightarrow{TN}+\overrightarrow{TM}=\vec{0}\quad\text{ et }\quad\overrightarrow{SC}+\overrightarrow{SB}=\vec{0}$$
Ainsi,
$$2\overrightarrow{AT}=-\dfrac{4}{3}\overrightarrow{AS}$$
D'où, $\boxed{\overrightarrow{AT}=-\dfrac{2}{3}\overrightarrow{AS}}$
 
Par conséquent, les points $A\;,\ S\ $ et $\ T$ sont alignés.

 

 

Exercice 28

Soit $ABC$ un triangle de centre de gravité $G\ $ et $\ I$ milieu de $[BC].$
 
1) Démontrons que pour tout point $M$ du plan :
$$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$$
$$2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}$$
Soit la relation : $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$
 
Alors, par la relation de Chasles, introduisons le point $G$ dans les vecteurs $\overrightarrow{MA}\;,\ \overrightarrow{MB}\ $ et $\ \overrightarrow{MC}.$
 
On obtient :
 
$\begin{array}{rcl}\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}&=&\left(\overrightarrow{MG}+\overrightarrow{GA}\right)+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)\\\\&=&\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\\\\&=&3\overrightarrow{MG}+\underbrace{\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}}_{=\vec{0}}\end{array}$
 
Or, $G$ est le centre de gravité du triangle $ABC.$
 
Ce qui entraine alors :
$$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$$
D'où, $\boxed{\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}}$
 
Soit la relation : $2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$
 
Alors, par la relation de Chasles, introduisons le point $I$ dans les vecteurs $\overrightarrow{MA}\;,\ \overrightarrow{MB}\ $ et $\ \overrightarrow{MC}.$
 
On obtient :
 
$\begin{array}{rcl}2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}&=&2\left(\overrightarrow{MI}+\overrightarrow{IA}\right)-\left(\overrightarrow{MI}+\overrightarrow{IB}\right)-\left(\overrightarrow{MI}+\overrightarrow{IC}\right)\\\\&=&2\overrightarrow{MI}+2\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB}-\overrightarrow{MI}-\overrightarrow{IC}\\\\&=&2\overrightarrow{IA}-\overrightarrow{IB}-\overrightarrow{IC}\\\\&=&2\overrightarrow{IA}-\left(\underbrace{\overrightarrow{IB}+\overrightarrow{IC}}_{=\vec{0}}\right)\end{array}$
 
Comme $I$ est le milieu de $[BC]$ alors,
$$\overrightarrow{IB}+\overrightarrow{IC}=\vec{0}$$
Par conséquent, $\boxed{2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}}$
 
2) Déterminons l'ensemble des points $M$ tels que les vecteurs $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\ $ et $\ 2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$ soient colinéaires.
 
En effet, d'après les résultats de la question $1\;)$, on a :
 
$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$
 
$2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}$
 
Donc, $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\ $ et $\ 2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$ colinéaires si, et seulement si, les vecteurs $3\overrightarrow{MG}\ $ et $\ 2\overrightarrow{IA}$ sont colinéaires.
 
Or, $3\overrightarrow{MG}\ $ et $\ 2\overrightarrow{IA}$ sont colinéaires si, et seulement si, les droites $(MG)\ $ et $\ (IA)$ sont parallèles.
 
$M$ appartient donc à la droite passant par $G$ et parallèle à $(IA).$
 
Mais on sait que la droite $(IA)$ ; médiane issue de $A$, passe aussi par le centre de gravité $G$ de ce triangle.
 
D'où, l'ensemble des points $M$ tels que les vecteurs $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\ $ et $\ 2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$ soient colinéaires est la droite $(IA).$
 
3) Déterminons l'ensemble des points $M$ tels que :
$$\left\|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right\|$$
En effet, d'après les résultats de la question $1\;)$, on a :
 
$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$
 
$2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}$
 
Donc, en remplaçant, on obtient :
 
$\begin{array}{rcl}\left\|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right\|&\Leftrightarrow&\left\|3\overrightarrow{MG}\right\|=\left\|2\overrightarrow{IA}\right\|\\\\&\Leftrightarrow&3\left\|\overrightarrow{MG}\right\|=2\left\|\overrightarrow{IA}\right\|\\\\&\Leftrightarrow&\left\|\overrightarrow{MG}\right\|=\dfrac{2}{3}\left\|\overrightarrow{IA}\right\|\end{array}$
 
D'où, l'ensemble des points $M$ tels que $\left\|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right\|$ est le cercle de centre $G$ et de rayon $\dfrac{2}{3}IA.$
 
Remarque :
 
$G$ centre de gravité alors, $AG=\dfrac{2}{3}IA.$
 
Donc, $A$ appartient au cercle de centre $G$ et de rayon $\dfrac{2}{3}IA.$
 
Par conséquent, l'ensemble des points $M$ vérifiant $\left\|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right\|$ est le cercle de centre $G$ et passant par $A.$

 

 

Exercice 29

$ABCD$ est un parallélogramme, $I$ milieu de $[AB]\ $ et $\ J$ celui de $[CD]$
 
1) Démontrons que les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
 
Pour cela, il suffit juste de montrer que les vecteurs $\overrightarrow{ID}\ $ et $\ \overrightarrow{BJ}$ sont colinéaires.
 
En utilisant la relation de Chasles, on a :
$$\overrightarrow{ID}=\overrightarrow{IB}+\overrightarrow{BJ}+\overrightarrow{JD}\quad(*)$$
Comme $I$ milieu de $[AB]\ $ et $\ J$ milieu de $[CD]$ alors :
 
$\overrightarrow{IB}=\dfrac{1}{2}\overrightarrow{AB}\ $ et $\ \overrightarrow{JD}=-\dfrac{1}{2}\overrightarrow{DC}$
 
Or, $\overrightarrow{AB}=\overrightarrow{DC}$ car $ABCD$ est un parallélogramme donc, $\overrightarrow{IB}=-\overrightarrow{JD}$
 
Par suite, en reportant dans l'égalité $(*)$, on obtient :
 
$\begin{array}{rcl}\overrightarrow{ID}&=&\overrightarrow{IB}+\overrightarrow{BJ}+\overrightarrow{JD}\\\\&=&-\overrightarrow{JD}+\overrightarrow{BJ}+\overrightarrow{JD}\\\\&=&\overrightarrow{BJ}\end{array}$
 
Ainsi, $\overrightarrow{ID}=\overrightarrow{BJ}$
 
Ce qui signifie que $\overrightarrow{ID}\ $ et $\ \overrightarrow{BJ}$ sont colinéaires.
 
Par conséquent, les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
 
Autre méthode :
 
On a : $\overrightarrow{IB}=\overrightarrow{DJ}$ alors, $IBJD$ est un parallélogramme.
 
Par suite, $\overrightarrow{ID}=\overrightarrow{BJ}$
 
D'où, les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
 
2) a) Construisons les points $M\ $ et $\ N$ tels que $\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AC}\ $ et  $\ \overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}$
 
b) Démontrons que les points $M\ $ et $\ N$ appartiennent respectivement aux droites $(ID)\ $ et $\ (JB)$
 
Pour cela, il suffit de prouver que $D\;,\ M\;,\ I$ sont alignés de même que $B\;,\ N\;,\ J$
 
Ce qui revient donc à montrer que $\overrightarrow{IM}=k\overrightarrow{ID}\ $ et  $\ \overrightarrow{JN}=k'\overrightarrow{JB}$ avec $k\ $ et $\ k'$ deux nombres réels.
 
On a :
 
$\begin{array}{rcl}\overrightarrow{IM}&=&\overrightarrow{IA}+\overrightarrow{AM}\quad\text{or, }\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AC}\\\\&=&\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{AC}\\\\&=&\overrightarrow{IA}+\dfrac{1}{3}\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\\\\&=&\dfrac{1}{3}\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{DC}\\\\&=&\dfrac{1}{3}\left(\overrightarrow{IA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\left(2\overrightarrow{IA}+\overrightarrow{DC}\right)\quad\text{or, }2\overrightarrow{IA}=\overrightarrow{BA}\\\\&=&\dfrac{1}{3}\overrightarrow{ID}+\dfrac{1}{3}\underbrace{\left(\overrightarrow{BA}+\overrightarrow{DC}\right)}_{=\vec{0}}\\\\&=&\dfrac{1}{3}\overrightarrow{ID}\end{array}$
 
Donc, $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}$
 
Ainsi, les points $D\;,\ M\;,\ I$ sont alignés et par conséquent, $M$ appartient à la droite $(ID).$
 
De la même manière, on a :
 
$\begin{array}{rcl}\overrightarrow{JN}&=&\overrightarrow{JC}+\overrightarrow{CN}\quad\text{or, }\overrightarrow{CN}=\dfrac{1}{3}\overrightarrow{CA}\\\\&=&\overrightarrow{JC}+\dfrac{1}{3}\overrightarrow{CA}\\\\&=&\overrightarrow{JC}+\dfrac{1}{3}\left(\overrightarrow{CB}+\overrightarrow{BA}\right)\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{2}{3}\overrightarrow{JC}+\dfrac{1}{3}\overrightarrow{BA}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{1}{3}\left(2\overrightarrow{JC}+\overrightarrow{BA}\right)\quad\text{or, }2\overrightarrow{JC}=\overrightarrow{DC}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{1}{3}\underbrace{\left(\overrightarrow{BA}+\overrightarrow{DC}\right)}_{=\vec{0}}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}\end{array}$
 
Donc, $\overrightarrow{JN}=\dfrac{1}{3}\overrightarrow{JB}$
 
Par suite, les points $J\;,\ N\;,\ B$ sont alignés.
 
D'où, $N$ appartient à la droite $(JB).$
 
3) Démontrons que $MINJ$ est un parallélogramme
 
Soit : $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}\ $ et $\ \overrightarrow{JN}=\dfrac{1}{3}\overrightarrow{JB}$
 
Or, d'après la question 1), on a : $\overrightarrow{ID}=\overrightarrow{BJ}$
 
Donc, $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}=\dfrac{1}{3}\overrightarrow{BJ}=-\overrightarrow{JN}$
 
Par suite, $\overrightarrow{IM}=\overrightarrow{NJ}$
 
D'où, $MINJ$ est un parallélogramme.
 
4) Soit $\{E\}=(ID)\cap(BC)$, montrons que $B$ est milieu de $[CE]$
 
En effet, dans le triangle $CDE$, la droite $(JB)$ parallèle à $(DE)$ et passant par $J$, milieu de $[CD]$, coupe $[CE]$ au point $B.$
 
Ainsi, d'après le théorème de la droite des milieux, $B$ est milieu de $[CE].$
 

Exercice 30

$ABCD$ est un parallélogramme, $E\ $ et $\ F$ deux points définis par :
$$\overrightarrow{AE}=-\dfrac{1}{2}\overrightarrow{AD}\quad\text{ et }\quad\overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{BA}$$
1) Exprimons $\overrightarrow{AC}\ $ et $\ \overrightarrow{AF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}.$
 
En effet, par la relation de Chasles, introduisons le point $B$ dans le vecteur $\overrightarrow{AC}.$
 
On obtient alors :
$$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$$
Or, $ABCD$ est un parallélogramme, donc :
$$\overrightarrow{BC}=\overrightarrow{AD}$$
Ainsi, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{AD}$, on trouve :
 
$\boxed{\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}}$
 
Soit : $\overrightarrow{AE}=-\dfrac{1}{2}\overrightarrow{AD}\ $ et $\ \overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{BA}.$
 
Alors, en additionnant membre à membre ces deux égalités, on obtient :
$$\underbrace{\overrightarrow{AE}+\overrightarrow{EF}}_{=\overrightarrow{AF}}=-\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{BA}$$
En appliquant la relation de Chasles, on trouve :
 
$\begin{array}{rcl}\overrightarrow{AF}&=&-\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{BA}\\\\&=&-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\end{array}$
 
D'où, $\boxed{\overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}}$
 
2) Démontrons que les points $A\;,\ F\ $ et $\ C$ sont alignés.
 
En effet, les points $A\;,\ F\ $ et $\ C$ sont alignés si, et seulement si, les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{AF}$ sont colinéaires.
 
Soit : $\overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}$
 
Alors, en mettant $-\dfrac{1}{2}$ en facteur, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AF}&=&-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\\\\&=&-\dfrac{1}{2}\left(\underbrace{\overrightarrow{AB}+\overrightarrow{AD}}_{=\overrightarrow{AC}}\right)\\\\&=&-\dfrac{1}{2}\overrightarrow{AC}\end{array}$
 
D'où, $\boxed{\overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AC}}$
 
Ce qui signifie que les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{AF}$ sont colinéaires.
 
Par conséquent, les points $A\;,\ F\ $ et $\ C$ sont alignés.
 
3) Exprimons les coordonnées de $A\;,\ F\ $ et $\ C$ dans le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AD}).$
 
En effet, dans le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AD})$, on a : $A$ origine du repère et $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$ constituent les vecteurs de base de ce repère.
 
Ainsi,
$$A\begin{pmatrix}0\\\\0\end{pmatrix}$$
Par ailleurs, d'après les résultats de la question $1\;)$, on a : 
$$\overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}$$
Donc, 
$$F\begin{pmatrix}-\dfrac{1}{2}\\\\-\dfrac{1}{2}\end{pmatrix}$$
De même, on a :
$$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$$
D'où, 
$$C\begin{pmatrix}1\\\\1\end{pmatrix}$$
Calculons les coordonnées de $\overrightarrow{AF}\ $ et $\ \overrightarrow{AC}$
 
Soit : $\overrightarrow{AF}\begin{pmatrix}x_{F}-x_{A}\\\\y_{F}-y_{A}\end{pmatrix}\ $ et $\ \overrightarrow{AC}\begin{pmatrix}x_{C}-x_{A}\\\\y_{C}-y_{A}\end{pmatrix}$
 
En remplaçant ces coordonnées par leur valeur, on trouve :
$$\overrightarrow{AF}\begin{pmatrix}-\dfrac{1}{2}\\\\-\dfrac{1}{2}\end{pmatrix}\quad\text{ et }\quad\overrightarrow{AC}\begin{pmatrix}1\\\\1\end{pmatrix}$$

 

 

Exercice 31

Soit $ABCD$ un parallélogramme. On considère $E$ défini par $\overrightarrow{CE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$ et le point $F$ symétrique de $D$ par rapport à $E.$
 
1) Démontrons que $E$ est le milieu de $[AB]\ $ et $\ B$ le milieu de $[CF].$
 
Soit : $\overrightarrow{CE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$
 
Alors, par la relation de Chasles, en introduisant le point $B$ dans le vecteur $\overrightarrow{CE}$, on obtient :
$$\overrightarrow{CB}+\overrightarrow{BE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$$
Or, $ABCD$ est un parallélogramme, donc :
$$\overrightarrow{CB}=\overrightarrow{DA}$$
Par suite, en remplaçant $\overrightarrow{CB}$ par $\overrightarrow{DA}$, on trouve :
$$\overrightarrow{DA}+\overrightarrow{BE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$$
Ainsi, en appliquant les propriétés du calcul vectoriel, on obtient :
 
$\begin{array}{rcl}\overrightarrow{DA}+\overrightarrow{BE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}&\Leftrightarrow&\overrightarrow{BE}=-\overrightarrow{DA}+\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{BE}=-\dfrac{1}{2}\overrightarrow{AB}\\\\&=&\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BA}\end{array}$
 
D'où, $\boxed{\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BA}}$
 
Ce qui démontre que $E$ est le milieu de $[AB].$
 
Pour montrer que $B$ est milieu de $[CF]$, il suffit de montrer que :
$$\overrightarrow{BC}+\overrightarrow{BF}=\vec{0}$$
Soit la somme vectorielle : $\overrightarrow{BC}+\overrightarrow{BF}$
 
Alors, par la relation de Chasles, introduisons le point $E$ dans le vecteur $\overrightarrow{BF}.$
 
On obtient :
$$\overrightarrow{BC}+\overrightarrow{BF}=\overrightarrow{BC}+\overrightarrow{BE}+\overrightarrow{EF}$$
Or, on sait que $ABCD$ est un parallélogramme, donc :
$$\overrightarrow{BC}=\overrightarrow{AD}$$
Par ailleurs, $F$ étant le symétrique de $D$ par rapport à $E$ alors,
$$\overrightarrow{EF}=\overrightarrow{DE}$$
Ainsi, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{AD}\ $ et $\ \overrightarrow{EF}$ par $\overrightarrow{DE}$, on obtient :
$$\overrightarrow{BC}+\overrightarrow{BF}=\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{DE}$$
D'après Chasles, on trouve :
$$\overrightarrow{BC}+\overrightarrow{BF}=\overrightarrow{AE}+\overrightarrow{BE}$$
Comme $E$ est milieu de $[AB]$ alors, $\overrightarrow{AE}+\overrightarrow{BE}=\vec{0}.$
 
D'où, $\boxed{\overrightarrow{BC}+\overrightarrow{BF}=\vec{0}}$
 
Ce qui démontre que $B$ est le milieu de $[CF].$
 
2) Démontrons que $ADBF$ est un parallélogramme
 
D'après les résultats de la question $1\;)$, on a : $E$ milieu de $[AB].$
 
Ce qui se traduit par :
$$\overrightarrow{AE}+\overrightarrow{BE}=\vec{0}$$
Par ailleurs, on sait que $F$ est le symétrique de $D$ par rapport à $E.$
 
Ce qui signifie que $E$ est le milieu de $[DF].$
 
Ce qui peut encore s'écrire :
$$\overrightarrow{DE}+\overrightarrow{FE}=\vec{0}$$
Alors, en additionnant membre à membre ces deux égalités, on trouve :
$$\overrightarrow{AE}+\overrightarrow{BE}+\overrightarrow{DE}+\overrightarrow{FE}=\vec{0}$$
Ce qui montre que $ADBF$ est un parallélogramme de centre $E.$

 

 
Autre méthode :
 
On a : dans le triangle $CDF$, la droite $(AB)$ passant par $E$ milieu de $[DF]$ coupe $[CF]$ au point $B.$
 
Donc, d'après la réciproque du théorème de la droite des milieux, $B$ est milieu de $[CF].$

Exercice 32

On considère l'hexagone régulier $ABCDEF$ de centre $O$ ci-dessus, et $I\ $ et $\ J$ les milieux respectifs des segments $[AB]\ $ et $\ [ED].$ En utilisant les lettres de la figure citons : 
 
a) deux vecteurs égaux
 
En effet, deux vecteurs sont égaux si, et seulement si, ils ont même direction, même sens et même norme ou longueur.
 
Ainsi, $\overrightarrow{AF}\ $ et $\ \overrightarrow{OE}$ sont deux vecteurs égaux.
 
b) deux vecteurs colinéaires de sens contraire et de normes distinctes.
 
$\overrightarrow{AD}\ $ et $\ \overrightarrow{CB}$ sont deux vecteurs colinéaires de sens contraire et de normes distinctes.
 
c) deux vecteurs colinéaires de même sens et de normes différentes.
 
$\overrightarrow{AB}\ $ et $\ \overrightarrow{JD}$ sont deux vecteurs colinéaires de même sens et de normes différentes.
 
d) deux vecteurs orthogonaux.
 
$\overrightarrow{IJ}\ $ et $\ \overrightarrow{FC}$ sont deux vecteurs orthogonaux.
 
e) deux vecteurs non colinéaires et de même norme. 
 
$\overrightarrow{EF}\ $ et $\ \overrightarrow{DC}$ sont deux vecteurs non colinéaires et de même norme.
 
f) deux vecteurs opposés.
 
En effet, deux vecteurs sont opposés si, et seulement si, ils ont même direction, même norme mais de sens contraire.
 
Ainsi, $\overrightarrow{IA}\ $ et $\ \overrightarrow{IB}$ sont deux vecteurs opposés.
 
g) deux vecteurs non colinéaires et de normes distinctes.
 
$\overrightarrow{AD}\ $ et $\ \overrightarrow{OB}$ sont deux vecteurs non colinéaires et de normes distinctes.

Exercice 33

On considère la figure ci-dessous :

 

 
1) Citons tous les vecteurs égaux à $\overrightarrow{AB}.$
 
Les vecteurs égaux à $\overrightarrow{AB}$ sont : $\overrightarrow{HE}\ $ et $\ \overrightarrow{GF}$
 
Ainsi, on a : $\boxed{\overrightarrow{AB}=\overrightarrow{HE}=\overrightarrow{GF}}$
 
2) Citons tous les vecteurs égaux à $\overrightarrow{FE}.$
 
Les vecteurs égaux à $\overrightarrow{FE}$ sont : $\overrightarrow{ED}\;,\ \overrightarrow{GH}\ $ et $\ \overrightarrow{BC}$
 
Donc, on a : $\boxed{\overrightarrow{FE}=\overrightarrow{ED}=\overrightarrow{GH}=\overrightarrow{BC}}$
 
3) Déterminons un ou plusieurs vecteurs égaux à $\overrightarrow{AB}+\overrightarrow{FE}.$
 
En effet, comme :
 
$\overrightarrow{AB}=\overrightarrow{HE}=\overrightarrow{GF}$
 
$\overrightarrow{FE}=\overrightarrow{ED}=\overrightarrow{GH}=\overrightarrow{BC}$
 
Alors, en remplaçant puis, en appliquant la relation de Chasles, on obtient :
 
$\overrightarrow{AB}+\overrightarrow{FE}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
 
$\overrightarrow{AB}+\overrightarrow{FE}=\overrightarrow{HE}+\overrightarrow{ED}=\overrightarrow{HD}$
 
$\overrightarrow{AB}+\overrightarrow{FE}=\overrightarrow{GF}+\overrightarrow{FE}=\overrightarrow{GE}$
 
Par conséquent, les vecteurs égaux à $\overrightarrow{AB}+\overrightarrow{FE}$ sont : $\overrightarrow{AC}\;,\ \overrightarrow{HD}\ $ et $\ \overrightarrow{GE}$
 
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{FE}=\overrightarrow{AC}=\overrightarrow{HD}=\overrightarrow{GE}}$
 
4) Déterminons un vecteur égal aux vecteurs suivants :
 
a) $\overrightarrow{AB}+\overrightarrow{AH}$
 
En effet, on a : $\overrightarrow{AB}=\overrightarrow{HE}.$
 
Donc, en remplaçant $\overrightarrow{AB}$ par $\overrightarrow{HE}$ puis, en appliquant la relation de Chasles, on obtient :
$$\overrightarrow{AB}+\overrightarrow{AH}=\overrightarrow{HE}+\overrightarrow{AH}=\overrightarrow{AE}$$
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{AH}=\overrightarrow{AE}}$
 
b) $\overrightarrow{BA}+\overrightarrow{BC}$
 
En effet, on a : $\overrightarrow{BA}=\overrightarrow{FG}\ $ et $\ \overrightarrow{BC}=\overrightarrow{GH}$
 
Donc, en remplaçant $\overrightarrow{BA}$ par $\overrightarrow{FG}\ $ et $\ \overrightarrow{BC}$ par $\overrightarrow{GH}$ puis, en appliquant la relation de Chasles, on obtient :
$$\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{FG}+\overrightarrow{GH}=\overrightarrow{FH}$$
Ainsi, $\boxed{\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{FH}}$
 
c) $\overrightarrow{BC}+\overrightarrow{DE}$
 
En effet, comme $\overrightarrow{BC}=\overrightarrow{ED}$ alors, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{ED}$ puis, en utilisant la relation de Chasles, on obtient :
$$\overrightarrow{BC}+\overrightarrow{DE}=\overrightarrow{ED}+\overrightarrow{DE}=\vec{0}$$
D'où, $\boxed{\overrightarrow{BC}+\overrightarrow{DE}=\vec{0}}$
 
d) $\overrightarrow{BF}+\overrightarrow{GF}$
 
En effet, on sait que : $\overrightarrow{AB}=\overrightarrow{GF}.$
 
Par suite, $ABFG$ est un parallélogramme.
 
Par conséquent, $\overrightarrow{BF}=\overrightarrow{AG}.$
 
Donc, en remplaçant $\overrightarrow{BF}$ par $\overrightarrow{AG}$ puis, en utilisant la relation de Chasles, on trouve :
$$\overrightarrow{BF}+\overrightarrow{GF}=\overrightarrow{AG}+\overrightarrow{GF}=\overrightarrow{AF}$$
D'où, $\boxed{\overrightarrow{BF}+\overrightarrow{GF}=\overrightarrow{AF}}$ 
 
e) $\overrightarrow{AE}+\overrightarrow{FB}$
 
En effet, comme $\overrightarrow{BC}=\overrightarrow{FE}$ alors, $BCEF$ est un parallélogramme.
 
Par conséquent, $\overrightarrow{FB}=\overrightarrow{EC}.$
 
Ainsi, en remplaçant $\overrightarrow{FB}$ par $\overrightarrow{EC}$ puis, en appliquant la relation de Chasles, on trouve :
$$\overrightarrow{AE}+\overrightarrow{FB}=\overrightarrow{AE}+\overrightarrow{EC}=\overrightarrow{AC}$$
D'où, $\boxed{\overrightarrow{AE}+\overrightarrow{FB}=\overrightarrow{AC}}$ 
 
N.B. Pour chacune des réponses, on utilisera uniquement les lettres de la figure.

Exercice 34

$A\;,\ B\;,\ C\;,\ D$ sont quatre points.
 
Démontrons que :
 
1) $\overrightarrow{AB}-\overrightarrow{CD}-(\overrightarrow{AB}-\overrightarrow{CA})=\overrightarrow{DA}$ 
 
En utilisant les propriétés du calcul vectoriel puis, en appliquant la relation de Chasles, on obtient :
 
$\begin{array}{rcl} \overrightarrow{AB}-\overrightarrow{CD}-(\overrightarrow{AB}-\overrightarrow{CA})&=&\overrightarrow{AB}+\overrightarrow{DC}-\overrightarrow{AB}+\overrightarrow{CA}\\\\&=&\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BA}+\overrightarrow{CA}\\\\&=&\underbrace{\overrightarrow{AB}+\overrightarrow{BA}}_{=\vec{0}}+\underbrace{\overrightarrow{DC}+\overrightarrow{CA}}_{=\overrightarrow{DA}}\\\\&=&\overrightarrow{DA}\end{array}$
 
D'où, $\boxed{\overrightarrow{AB}-\overrightarrow{CD}-(\overrightarrow{AB}-\overrightarrow{CA})=\overrightarrow{DA}}$ 
 
2) $\overrightarrow{AD}+\overrightarrow{BC}=(\overrightarrow{AC}+\overrightarrow{BD})$
 
Par la relation de Chasles, introduisons le point $D$ dans le vecteur $\overrightarrow{BC}$ puis, appliquons les propriétés du calcul vectoriel
 
On obtient alors :
 
$\begin{array}{rcl} \overrightarrow{AD}+\overrightarrow{BC}&=&\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{DC}\\\\&=&\underbrace{\overrightarrow{AD}+\overrightarrow{DC}}_{=\overrightarrow{AC}}+\overrightarrow{BD}\\\\&=&\overrightarrow{AC}+\overrightarrow{BD}\end{array}$
 
D'où, $\boxed{\overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{BD}}$ 

Exercice 35

Écrivons les vecteurs suivants en utilisant le moins de vecteurs possibles :
 
Soit : $\vec{u}=\overrightarrow{DE}+\overrightarrow{AB}-\overrightarrow{DB}$ (1 vecteur)
 
En effet, en utilisant les propriétés du calcul vectoriel puis, en appliquant la relation de Chasles, on obtient :
 
$\begin{array}{rcl} \vec{u}&=&\overrightarrow{DE}+\overrightarrow{AB}-\overrightarrow{DB}\\\\&=&\overrightarrow{DE}+\underbrace{\overrightarrow{AB}+\overrightarrow{BD}}_{=\overrightarrow{AD}}\\\\&=&\overrightarrow{DE}+\overrightarrow{AD}\\\\&=&\underbrace{\overrightarrow{AD}+\overrightarrow{DE}}_{=\overrightarrow{AE}}\end{array}$
 
D'où, $\boxed{\vec{u}=\overrightarrow{AE}}$ 
 
Soit : $\vec{v}=2(\overrightarrow{AB}+\overrightarrow{AC})+\overrightarrow{BC}$ (2 vecteurs)
 
Alors, en appliquant la relation de Chasles puis, les propriétés du calcul vectoriel, on obtient :
 
$\begin{array}{rcl} \vec{v}&=&2\left(\overrightarrow{AB}+\overrightarrow{AC}\right)+\overrightarrow{BC}\\\\&=&2\overrightarrow{AB}+2\overrightarrow{AC}+\overrightarrow{BC}\\\\&=&\overrightarrow{AB}+\underbrace{\overrightarrow{AB}+\overrightarrow{BC}}_{=\overrightarrow{AC}}+2\overrightarrow{AC}\\\\&=&\overrightarrow{AB}+\overrightarrow{AC}+2\overrightarrow{AC}\\\\&=&\overrightarrow{AB}+3\overrightarrow{AC}\end{array}$
 
D'où, $\boxed{\vec{v}=\overrightarrow{AB}+3\overrightarrow{AC}}$ 
 
Soit : $\vec{w}=\dfrac{1}{2}\overrightarrow{BA}-2\left(\overrightarrow{DB}-\dfrac{1}{4}\overrightarrow{AC}\right)$ (2 vecteurs)
 
Alors,  en appliquant les propriétés du calcul vectoriel puis, la relation de Chasles, on obtient :
 
$\begin{array}{rcl} \vec{w}&=&\dfrac{1}{2}\overrightarrow{BA}-2\left(\overrightarrow{DB}-\dfrac{1}{4}\overrightarrow{AC}\right)\\\\&=&\dfrac{1}{2}\overrightarrow{BA}-2\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{AC}\\\\&=&\dfrac{1}{2}\left(\underbrace{\overrightarrow{BA}+\overrightarrow{AC}}_{=\overrightarrow{BC}}\right)+2\overrightarrow{BD}\\\\&=&\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{BD}\end{array}$
 
D'où, $\boxed{\vec{w}=\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{BD}}$ 

Exercice 36

$O\ $ et $\ A$ sont deux points distincts :
 
1) Plaçons les points $M\;,\ N\;,\ P$ tels que :
 
a) $\overrightarrow{OM}=2\overrightarrow{OA}$
 
b) $\overrightarrow{ON}=-3.5\overrightarrow{OA}=-\dfrac{7}{2}\overrightarrow{OA}$
 
c) $\overrightarrow{OP}=-7\overrightarrow{OA}$
 
2) a) Exprimons le vecteur $\overrightarrow{OM}+\overrightarrow{ON}$ en fonction de $\overrightarrow{OA}.$
 
En effet, d'après la question $1\;)$ on a :
 
$\overrightarrow{OM}=2\overrightarrow{OA}$
 
$\overrightarrow{ON}=-\dfrac{7}{2}\overrightarrow{OA}$
 
Donc, en remplaçant $\overrightarrow{OM}\ $ et $\ \overrightarrow{ON}$ par leur expression puis, en appliquant les propriétés du calcul vectoriel, on trouve :
 
$\begin{array}{rcl} \overrightarrow{OM}+\overrightarrow{ON}&=&2\overrightarrow{OA}-\dfrac{7}{2}\overrightarrow{OA}\\\\&=&\dfrac{4}{2}\overrightarrow{OA}-\dfrac{7}{2}\overrightarrow{OA}\\\\&=&-\dfrac{3}{2}\overrightarrow{OA}\end{array}$
 
D'où, $\boxed{\overrightarrow{OM}+\overrightarrow{ON}=-\dfrac{3}{2}\overrightarrow{OA}}$ 
 
b) Exprimons le vecteur $\overrightarrow{OP}$ en fonction de $\overrightarrow{ON}.$
 
On a : $\overrightarrow{OP}=-7\overrightarrow{OA}$
 
Or, on sait que :
 
$\begin{array}{rcl}\overrightarrow{ON}&=&-3.5\overrightarrow{OA}\\\\&=&\dfrac{-7}{2}\overrightarrow{OA}\\\\&=&\dfrac{-7\overrightarrow{OA}}{2}\quad\text{ Or, on sait que :}\ -7\overrightarrow{OA}=\overrightarrow{OP}\\\\&=&\dfrac{\overrightarrow{OP}}{2}\end{array}$
 
Ainsi,
$$\overrightarrow{ON}=\dfrac{\overrightarrow{OP}}{2}$$
D'où, $\boxed{\overrightarrow{OP}=2\overrightarrow{ON}}$ 

Exercice 37

$A\;,\ B\;,\ C\ $ et $\ D$ sont quatre points quelconques du plan.
 
1) Construisons les points $R\ $ et $\ S$ tels que :
$$\overrightarrow{AR}=\overrightarrow{AB}+\overrightarrow{CD}\quad\text{ et }\quad\overrightarrow{AS}=\overrightarrow{AD}+\overrightarrow{CB}$$


 
Nous remarquons que $R=S$ ; autrement dit, les points $R\ $ et $\ S$ sont confondus.
 
2) Démontrons que :
$$\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$$
En effet, par la relation de Chasles, en introduisant le point $C$ dans le vecteur $\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AB}+\overrightarrow{CD}&=&\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{CD}\\\\&=&\underbrace{\overrightarrow{AC}+\overrightarrow{CD}}_{=\overrightarrow{AD}}+\overrightarrow{CB}\\\\&=&\overrightarrow{AD}+\overrightarrow{CB}\end{array}$
 
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}}$
 
Par ailleurs, d'après le résultat de la question $1\,)$, on a : les points $R\ $ et $\ S$ confondus.
 
Ce qui entraine,
$$\overrightarrow{AR}=\overrightarrow{AS}$$
Or, on sait que :
$$\overrightarrow{AR}=\overrightarrow{AB}+\overrightarrow{CD}\quad\text{ et }\quad\overrightarrow{AS}=\overrightarrow{AD}+\overrightarrow{CB}$$
Par conséquent, $\boxed{\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}}$

Exercice 38

$ABCD$ est un parallélogramme de centre $O.$
 
1) Calculons la somme vectorielle :
$$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}$$
En effet, comme $ABCD$ est un parallélogramme de centre $O$ alors, $O$ est le milieu de $[AC]$ et de $[BD].$
 
Par suite :
$$\overrightarrow{OA}+\overrightarrow{OC}=\vec{0}\quad\text{et}\quad\overrightarrow{OB}+\overrightarrow{OD}=\vec{0}$$
Par conséquent,
 
$\begin{array}{rcl}\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}&=&\underbrace{\overrightarrow{OA}+\overrightarrow{OC}}_{=\vec{0}}+\underbrace{\overrightarrow{OB}+\overrightarrow{OD}}_{=\vec{0}}\\\\&=&\vec{0}\end{array}$
 
D'où, $\boxed{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\vec{0}}$
 
2) $M$ étant un point quelconque du plan, plaçons les points $E\;,\ F\;,\ G\ $ et $\ H$ tels que :
$$\overrightarrow{ME}=\overrightarrow{AB}\;;\ \overrightarrow{MF}=\overrightarrow{BC}\;;\ \overrightarrow{MG}=\overrightarrow{CD}\quad\text{et}\quad\overrightarrow{MH}=\overrightarrow{DA}$$
Démontrons que le quadrilatère $EFGH$ est un parallélogramme.
 
Pour cela, calculons la somme vectorielle :
$$\overrightarrow{ME}+\overrightarrow{MF}+\overrightarrow{MG}+\overrightarrow{MH}$$
On a :
 
$\begin{array}{rcl}\overrightarrow{ME}+\overrightarrow{MF}+\overrightarrow{MG}+\overrightarrow{MH}&=&\underbrace{\overrightarrow{AB}+\overrightarrow{BC}}_{=\overrightarrow{AC}}+\underbrace{\overrightarrow{CD}+\overrightarrow{DA}}_{=\overrightarrow{CA}}\\\\&=&\overrightarrow{AC}+\overrightarrow{CA}\\\\&=&\vec{0}\end{array}$
 
Ainsi, $\boxed{\overrightarrow{ME}+\overrightarrow{MF}+\overrightarrow{MG}+\overrightarrow{MH}=\vec{0}}$
 
Par conséquent, $EFGH$ est un parallélogramme de centre $M.$

 

Exercice 39

$OAB$ est un triangle, $D\ $ et $\ C$ les points tels que :
$$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OB}\quad\text{ et }\quad\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0}$$
1) Démontrons que $O$ est le milieu de $[CD].$
 
En effet, $O$ est le milieu du segment $[CD]$ si, et seulement si :
$$\overrightarrow{OD}+\overrightarrow{OC}=\vec{0}$$
On a :
$$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0}$$
Or, on sait que :
$$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OB}$$
Donc, en remplaçant $\overrightarrow{OA}+\overrightarrow{OB}$ par $\overrightarrow{OD}$, on obtient :
$$\overrightarrow{OD}+\overrightarrow{OC}=\vec{0}$$
Ce qui montre que $O$ est le milieu de $[CD].$
 
2) $E\ $ et $\ F$ sont les points tels que :
$$\overrightarrow{OE}=\overrightarrow{OA}+\overrightarrow{OC}\quad\text{ et }\quad\overrightarrow{OF}=\overrightarrow{OB}+\overrightarrow{OC}$$
Démontons que $ABFE$ est un parallélogramme
 
Pour cela, calculons la somme vectorielle :
$$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OF}+\overrightarrow{OE}$$
Alors, en remplaçant, $\overrightarrow{OE}\ $ et $\ \overrightarrow{OF}$ par leur expression, on obtient :
 
$\begin{array}{rcl}\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OF}+\overrightarrow{OE}&=&\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OA}+\overrightarrow{OC}\\\\&=&\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\\\\&=&2\left(\underbrace{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}_{=\vec{0}}\right)\\\\&=&\vec{0}\end{array}$
 
Ainsi, $\boxed{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OF}+\overrightarrow{OE}=\vec{0}}$
 
Par conséquent, $ABFE$ est un parallélogramme de centre $O.$
 
Autre méthode :
 
Pour montrer que $ABFE$ est un parallélogramme, il suffit de montrer que :
$$\overrightarrow{AB}=\overrightarrow{EF}$$
En effet, on a : $\overrightarrow{OF}=\overrightarrow{OB}+\overrightarrow{OC}$
 
Donc, par la relation de Chasles, introduisons le point $E$ dans le vecteur $\overrightarrow{OF}.$
 
On obtient alors :
$$\overrightarrow{OE}+\overrightarrow{EF}=\overrightarrow{OB}+\overrightarrow{OC}\ \Rightarrow\ \overrightarrow{EF}=\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OE}$$
Ainsi, en remplaçant $\overrightarrow{OE}$ par son expression puis, en utilisant la relation de Chasles et les propriétés du calcul vectoriel, on trouve :
 
$\begin{array}{rcl}\overrightarrow{EF}&=&\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OE}\\\\&=&\overrightarrow{OB}+\overrightarrow{OC}-\left(\overrightarrow{OA}+\overrightarrow{OC}\right)\\\\&=&\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OA}-\overrightarrow{OC}\\\\&=&\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{AO}+\overrightarrow{CO}\\\\&=&\underbrace{\overrightarrow{AO}+\overrightarrow{OB}}_{=\overrightarrow{AB}}+\underbrace{\overrightarrow{OC}+\overrightarrow{CO}}_{=\vec{0}}\\\\&=&\overrightarrow{AB}\end{array}$
 
D'où, $\boxed{\overrightarrow{EF}=\overrightarrow{AB}}$
 
Par conséquent, le quadrilatère $ABFE$ est un parallélogramme.

 
 
 
 

Exercice 40

$A\;,\ B\;,\ C\;,\ D$ sont quatre points
 
1) Construisons les points $E\;,\ F$ tels que :
$$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}\quad\text{ et }\quad\overrightarrow{AF}=\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}$$
On a :
 
$\begin{array}{rcl}\overrightarrow{AE}&=&\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}\\\\&=&\overrightarrow{AB}+\underbrace{\overrightarrow{AC}+\overrightarrow{CB}}_{=\overrightarrow{AB}}\\\\&=&\overrightarrow{AB}+\overrightarrow{AB}\\\\&=&2\overrightarrow{AB}\end{array}$
 
Donc, $\boxed{\overrightarrow{AE}=2\overrightarrow{AB}}$
 
On peut ainsi utiliser cette nouvelle expression du vecteur $\overrightarrow{AE}$ pour construire le point $E.$
 
De la même manière, on a :
 
$\begin{array}{rcl}\overrightarrow{AF}&=&\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}\\\\&=&\overrightarrow{AB}+\underbrace{\overrightarrow{CA}+\overrightarrow{AD}}_{=\overrightarrow{CD}}\\\\&=&\overrightarrow{AB}+\overrightarrow{CD}\end{array}$
 
Ainsi, $\boxed{\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{CD}}$
 
Par conséquent, on peut utiliser cette nouvelle expression de $\overrightarrow{AF}$ pour construire le point $F.$

 
 
 
2) Montrons que :
$$\overrightarrow{FE}=\overrightarrow{AC}+\overrightarrow{DB}$$
En effet, on a : $\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}$
 
Alors, en introduisant le point $F$ dans le vecteur $\overrightarrow{AE}$, par la relation de Chasles, on obtient :
$$\overrightarrow{AF}+\overrightarrow{FE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}$$
Ce qui entraine :
$$\overrightarrow{FE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}-\overrightarrow{AF}$$
Or, on sait que : $\overrightarrow{AF}=\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}$
 
Donc, en remplaçant $\overrightarrow{AF}$ par $\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}$ puis, en utilisant les propriétés du calcul vectoriel et la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{FE}&=&\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}-\overrightarrow{AF}\\\\&=&\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}-\left(\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}\right)\\\\&=&\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}-\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AD}\\\\&=&\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{DA}\\\\&=&\underbrace{\overrightarrow{AB}+\overrightarrow{BA}}_{=\vec{0}}+\underbrace{\overrightarrow{DA}+\overrightarrow{AC}+\overrightarrow{CB}}_{=\overrightarrow{DB}}+\overrightarrow{AC}\\\\&=&\overrightarrow{DB}+\overrightarrow{AC}\end{array}$
 
D'où, $\boxed{\overrightarrow{FE}=\overrightarrow{AC}+\overrightarrow{DB}}$
 

Exercice 41

 
 
Sur la figure, les quadrilatères $SALE\;,\ SAIC\;,\ SCAE\;,\ BAEL\;,\ LAIB\ $ et $\ BACI$ sont des parallélogrammes.
 
En n'utilisant que les points de la figure, écrire chacune des sommes suivantes sous forme d'un seul vecteur.
 
a) $\overrightarrow{AB}+\overrightarrow{AL}=\overrightarrow{CB}$
 
En effet, $SALE$ étant un parallélogramme alors,
$$\overrightarrow{AL}=\overrightarrow{SE}$$
Par ailleurs, comme $SCAE$ est un parallélogramme alors,
$$\overrightarrow{SE}=\overrightarrow{CA}$$
Par conséquent,
$$\overrightarrow{AL}=\overrightarrow{CA}$$
Ainsi, en remplaçant $\overrightarrow{AL}$ par $\overrightarrow{CA}$ puis, en utilisant la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AB}+\overrightarrow{AL}&=&\overrightarrow{AB}+\overrightarrow{CA}\\\\&=&\overrightarrow{CA}+\overrightarrow{AB}\\\\&=&\overrightarrow{CB}\end{array}$
 
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{AL}=\overrightarrow{CB}}$
 
b) $\overrightarrow{AB}+\overrightarrow{BL}+\overrightarrow{LA}=\overrightarrow{AA}=\vec{0}$
 
En appliquant la relation de Chasles et les propriétés du calcul vectoriel, on obtient ce résultat.
 
c) $\overrightarrow{AB}-\overrightarrow{AL}=\overrightarrow{LB}$
 
En utilisant les propriétés du calcul vectoriel puis, la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AB}-\overrightarrow{AL}&=&\overrightarrow{AB}+\overrightarrow{LA}\\\\&=&\overrightarrow{LA}+\overrightarrow{AB}\\\\&=&\overrightarrow{LB}\end{array}$
 
D'où, $\boxed{\overrightarrow{AB}-\overrightarrow{AL}=\overrightarrow{LB}}$
 
d) $\overrightarrow{AB}+\overrightarrow{AL}+\overrightarrow{AE}=\overrightarrow{CL}$
 
En effet, d'après le résultat de la question $a\;)$, on a :
$$\overrightarrow{AB}+\overrightarrow{AL}=\overrightarrow{CB}$$
Or, $BAEL$ est un parallélogramme. Donc,
$$\overrightarrow{AE}=\overrightarrow{BL}$$
Ainsi, en remplaçant $\overrightarrow{AE}$ par $\overrightarrow{BL}$ puis, en utilisant la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AB}+\overrightarrow{AL}+\overrightarrow{AE}&=&\overrightarrow{CB}+\overrightarrow{BL}\\\\&=&\overrightarrow{CL}\end{array}$
 
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{AL}+\overrightarrow{AE}=\overrightarrow{CL}}$
 
e) $\overrightarrow{AE}-\left(\overrightarrow{CA}+\overrightarrow{SC}\right)=\overrightarrow{IS}$
 
En utilisant les propriétés du calcul vectoriel puis, la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AE}-\left(\overrightarrow{CA}+\overrightarrow{SC}\right)&=&\overrightarrow{AE}-\left(\overrightarrow{SC}+\overrightarrow{CA}\right)\\\\&=&\overrightarrow{AE}-\overrightarrow{SA}\\\\&=&\overrightarrow{AE}+\overrightarrow{AS}\end{array}$
 
Or, on sait que : $SCAE$ est un parallélogramme.
 
Donc,
$$\overrightarrow{AE}=\overrightarrow{CS}$$
De même, $SAIC$ étant un parallélogramme alors,
$$\overrightarrow{CS}=\overrightarrow{IA}$$
Par conséquent,
$$\overrightarrow{AE}=\overrightarrow{IA}$$
Ainsi, en remplaçant $\overrightarrow{AE}$ par $\overrightarrow{IA}$ puis, en appliquant la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{AE}-\left(\overrightarrow{CA}+\overrightarrow{SC}\right)&=&\overrightarrow{AE}+\overrightarrow{AS}\\\\&=&\overrightarrow{IA}+\overrightarrow{AS}\\\\&=&\overrightarrow{IS}\end{array}$
 
D'où, $\boxed{\overrightarrow{AE}-\left(\overrightarrow{CA}+\overrightarrow{SC}\right)=\overrightarrow{IS}}$
 
f) $\overrightarrow{SA}-\overrightarrow{LB}=\overrightarrow{SE}$
 
En effet, comme $BAEL$ est un parallélogramme alors, on a :
$$\overrightarrow{LB}=\overrightarrow{EA}$$
Donc, en remplaçant $\overrightarrow{BL}$ par $\overrightarrow{AE}$ puis, en utilisant les propriétés du calcul vectoriel et la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{SA}-\overrightarrow{LB}&=&\overrightarrow{SA}-\overrightarrow{EA}\\\\&=&\overrightarrow{SA}+\overrightarrow{AE}\\\\&=&\overrightarrow{SE}\end{array}$
 
D'où, $\boxed{\overrightarrow{SA}-\overrightarrow{LB}=\overrightarrow{SE}}$
 
g) $\overrightarrow{SI}-\overrightarrow{EL}-\overrightarrow{SL}=\overrightarrow{LC}$
 
En effet, $SALE$ est un parallélogramme donc,
$$\overrightarrow{EL}=\overrightarrow{SA}$$
Par ailleurs, comme $SAIC$ est un parallélogramme alors,
$$\overrightarrow{SA}=\overrightarrow{CI}$$
Par conséquent,
$$\overrightarrow{EL}=\overrightarrow{CI}$$
Ainsi, en remplaçant $\overrightarrow{EL}$ par $\overrightarrow{CI}$ puis, en utilisant les propriétés du calcul vectoriel et la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{SI}-\overrightarrow{EL}-\overrightarrow{SL}&=&\overrightarrow{SI}-\overrightarrow{CI}-\overrightarrow{SL}\\\\&=&\overrightarrow{SI}+\overrightarrow{IC}+\overrightarrow{LS}\\\\&=&\overrightarrow{LS}+\overrightarrow{SI}+\overrightarrow{IC}\\\\&=&\overrightarrow{LC}\end{array}$
 
D'où, $\boxed{\overrightarrow{SI}-\overrightarrow{EL}-\overrightarrow{SL}=\overrightarrow{LC}}$
 
h) $\overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}=\overrightarrow{SB}$ 
 
En effet, en utilisant les propriétés du calcul vectoriel puis, la relation de Chasles, on a :
 
$\begin{array}{rcl}\overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}&=&\overrightarrow{SI}+\underbrace{\overrightarrow{SL}+\overrightarrow{LE}}_{=\overrightarrow{SE}}\\\\&=&\overrightarrow{SI}+\overrightarrow{SE}\end{array}$
 
Or, on sait que $SCAE$ est un parallélogramme.
 
Donc, on a :
$$\overrightarrow{SE}=\overrightarrow{CA}$$
Par ailleurs, $BACI$ étant un parallélogramme alors, on a :
$$\overrightarrow{CA}=\overrightarrow{IB}$$
Par conséquent :
$$\overrightarrow{SE}=\overrightarrow{IB}$$
Ainsi, en remplaçant $\overrightarrow{SE}$ par $\overrightarrow{IB}$ puis, en appliquant la relation de Chasles, on obtient :
 
$\begin{array}{rcl}\overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}&=&\overrightarrow{SI}+\overrightarrow{SE}\\\\&=&\underbrace{\overrightarrow{SI}+\overrightarrow{IB}}_{=\overrightarrow{SB}}\\\\&=&\overrightarrow{SB}\end{array}$
 
D'où, $\boxed{\overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}=\overrightarrow{SB}}$
 

Exercice 45

Dans un triangle $ABC$, on considère par $M$ le milieu de $[AB]$, par $I$ celui de $[MC]\ $ et $\ K$ le point tel que $\overrightarrow{CK}=\dfrac{1}{3}\overrightarrow{CB}$
 
1) Montrons que :
$$\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\quad\text{et}\quad\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}$$
On a :
 
$\begin{array}{rcl}\overrightarrow{AI}&=&\overrightarrow{AC}+\overrightarrow{CI}\quad\text{or, }I\ \text{ milieu de }[CM]\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CM}\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\left(\overrightarrow{CA}+\overrightarrow{AM}\right)\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AM}\quad\text{or, }M\ \text{ milieu de }[AB]\\\\&=&\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}\right)\\\\&=&\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{4}\overrightarrow{AB}\end{array}$
 
D'où, $\boxed{\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}}$
 
Soit :
 
$\begin{array}{rcl}\overrightarrow{AK}&=&\overrightarrow{AC}+\overrightarrow{CK}\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\left(\overrightarrow{CA}+\overrightarrow{AB}\right)\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\\\\&=&\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{AB}\\\\&=&\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{AB}\end{array}$
 
Alors, $\boxed{\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}}$
 
2) En déduisons que les points $A\;,\ I\;,\ K$ sont alignés.
 
Pour cela, il suffit de montrer que $\overrightarrow{AI}=\alpha\overrightarrow{AK}$ avec $\alpha$ un nombre réel non nul.
 
D'après la question précédente, on peut constater que $4\overrightarrow{AI}=3\overrightarrow{AK}$
 
Ainsi, $\overrightarrow{AI}=\dfrac{3}{4}\overrightarrow{AK}$
 
D'où, les points $A\;,\ I\;,\ K$ sont alignés.
 
Autre méthode :
 
D'après le résultat de la question $1\;)$, on a :
 
$\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}$
 
$\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}$
 
Donc, dans le repère $\left(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$, les coordonnées des vecteurs $\overrightarrow{AI}\ $ et $\ \overrightarrow{AK}$ sont données par :
$$\overrightarrow{AI}\begin{pmatrix}\dfrac{1}{4}\\ \\\dfrac{1}{2}\end{pmatrix}\quad \text{et}\quad \overrightarrow{AK}\begin{pmatrix}\dfrac{1}{3}\\ \\\dfrac{2}{3}\end{pmatrix}$$
Calculons alors les rapports : $\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AK}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AK}}}}$
 
Soit :
 
$\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AK}}}}=\dfrac{\dfrac{1}{4}}{\dfrac{1}{3}}=\dfrac{1}{4}\times\dfrac{3}{1}=\dfrac{3}{4}$
 
$\dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AK}}}}=\dfrac{\dfrac{1}{2}}{\dfrac{2}{3}}=\dfrac{1}{2}\times\dfrac{3}{2}=\dfrac{3}{4}$
 
On trouve alors une même valeur égale à $\dfrac{3}{4}.$
 
Ce qui signifie que les points $A\;,\ I\;,\ K$ sont alignés.
 
Explication :
 
En effet, on a :
$$\left\lbrace\begin{array}{lcl}\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AK}}}}&=&\dfrac{3}{4}\\ \\\dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AK}}}}&=&\dfrac{3}{4}\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl} x_{_{\overrightarrow{AI}}}&=&\dfrac{3}{4}\times x_{_{\overrightarrow{AK}}}\\ \\y_{_{\overrightarrow{AI}}}&=&\dfrac{3}{4}\times y_{_{\overrightarrow{AK}}}\end{array}\right.$$
Par conséquent, $\overrightarrow{AI}=\dfrac{3}{4}\overrightarrow{AK}$
 
Ce qui montre que les points $A\;,\ I\ $ et $\ K$ sont alignés.
 

Exercice 51

$ABCD$ est un trapèze tel que $\overrightarrow{BC}=2\overrightarrow{AD}$
 
Soit $k$ un réel et $M$ le point défini par $\overrightarrow{AM}=k\overrightarrow{AB}$
 
$M$ se projette en $K$ sur $(AC)$ parallèlement à $(BC)$ et en $N$ sur $(CD)$ parallèlement à $(BC)$

 

 
1) Montrons que $\overrightarrow{MK}=2k\overrightarrow{AD}\ $ et $\ \overrightarrow{NK}=(k-1)\overrightarrow{AD}$
 
On constate que $AMK\ $ et $\ ABC$ sont deux triangles en situation de Thalès donc, en appliquant le théorème de Thalès, on obtient :
$$\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{MK}}{\overline{BC}}\qquad(1)$$
Or, $\overrightarrow{AM}=k\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}=2\overrightarrow{AD}$
 
Donc, $\overline{AM}=k\overline{AB}\ $ et $\ \overline{BC}=2\overline{AD}$
 
Par suite, en remplaçant dans (1), on aura :
 
$\begin{array}{rcl}\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{MK}}{\overline{BC}}&\Leftrightarrow&\dfrac{k\overline{AB}}{\overline{AB}}=\dfrac{\overline{MK}}{2\overline{AD}}\\ \\&\Leftrightarrow&\dfrac{\overline{MK}}{2\overline{AD}}=k\\ \\&\Leftrightarrow&\overline{MK}=2k\overline{AD}\end{array}$
 
De plus $(MK)$ parallèle à $(BC)$ qui est parallèle à $(AD)$ donc, $(MK)$ est parallèle à $(AD)$
 
Ainsi, $\overline{MK}=2k\overline{AD}\ $ et $\ (MK)$ est parallèle à $(AD)$ telles que $[MK)\ $ et $\ [AD)$ orientées dans le même sens.
 
Par conséquent, $\overrightarrow{MK}=2k\overrightarrow{AD}\ $
 
Par ailleurs, on a : $\overrightarrow{MK}+\overrightarrow{KN}=\overrightarrow{MN}$
 
ce qui donne : $\overrightarrow{NK}=\overrightarrow{MK}-\overrightarrow{MN}$
 
Considérons $E$ le projeté de $D$ sur $(BC)$ parallèlement à $(AB)$ et $L$ le projeté de $M$ sur $(DE)$ parallèlement à $(BC)$
 
On a : $\overrightarrow{MN}=\overrightarrow{ML}+\overrightarrow{LN}$
 
Or, $\overrightarrow{ML}=\overrightarrow{AD}$ donc, $\overline{ML}=\overline{AD}$ 
 
De plus, les triangles $DLN\ $ et $\ DEC$ étant en position de Thalès alors, 
$$\dfrac{\overline{DL}}{\overline{DE}}=\dfrac{\overline{LN}}{\overline{EC}}\qquad(2)$$
Comme $\overline{DL}=\overline{AM}=k\overline{AB}\;;\ \overline{DE}=\overline{AB}\ $ et $\ \overline{EC}=\dfrac{1}{2}\overline{BC}=\overline{AD}$ alors, en remplaçant dans (2), on obtient :
 
$\begin{array}{rcl}\dfrac{\overline{DL}}{\overline{DE}}=\dfrac{\overline{LN}}{\overline{EC}}&\Leftrightarrow&\dfrac{k\overline{AB}}{\overline{AB}}=\dfrac{\overline{LN}}{\overline{AD}}\\ \\&\Leftrightarrow&\dfrac{\overline{LN}}{\overline{AD}}=k\\ \\&\Leftrightarrow&\overline{LN}=k\overline{AD}\end{array}$
 
Par ailleurs, comme $(LN)$ est parallèle à $(AD)$ avec $[LN)\ $ et $\ [AD)$ orientées dans le même sens alors, on peut conclure que $\overrightarrow{LN}=k\overrightarrow{AD}$
 
Ainsi, $\overrightarrow{MN}=\overrightarrow{ML}+\overrightarrow{LN}$
 
avec, $\overrightarrow{ML}=\overrightarrow{AD}\ $ et $\ \overrightarrow{LN}=k\overrightarrow{AD}$
 
Par suite, $\overrightarrow{MN}=\overrightarrow{AD}+k\overrightarrow{AD}$
 
Par conséquent, on aura :
 
$\begin{array}{rcl}\overrightarrow{NK}&=&\overrightarrow{MK}-\overrightarrow{MN}\\\\&=&2k\overrightarrow{AD}-(\overrightarrow{AD}+k\overrightarrow{AD})\\\\&=&(2k-k-1)\overrightarrow{AD}\\\\&=&(k-1)\overrightarrow{AD}\end{array}$
 
D'où, $\overrightarrow{NK}=(k-1)\overrightarrow{AD}$
 
2) Déterminons le réel $k$ pour que $K$ soit le milieu de $[MN]$
 
$K$ milieu de $[MN]$ si, et seulement si, $\overrightarrow{MK}+\overrightarrow{NK}=\vec{0}$
 
On a :
 
$\begin{array}{rcl}\overrightarrow{MK}+\overrightarrow{NK}=\vec{0}&\Leftrightarrow&2k\overrightarrow{AD}+(k-1)\overrightarrow{AD}=\vec{0}\\ \\&\Leftrightarrow&(2k+k-1)\overrightarrow{AD}=\vec{0}\quad\text{or, }\ \overrightarrow{AD}\neq\vec{0}\\ \\&\Leftrightarrow&3k-1=0\\ \\&\Leftrightarrow&k=\dfrac{1}{3}\end{array}$
 
Ainsi, $K$ milieu de $[MN]$ si, et seulement si, $k=\dfrac{1}{3}$
 
Déterminons le réel $k$ pour que $\overrightarrow{MN}=\dfrac{3}{2}\overrightarrow{AD}$
 
On sait que : $\overrightarrow{MN}=\overrightarrow{MK}-\overrightarrow{NK}$
 
Donc,
 
$\begin{array}{rcl}\overrightarrow{MN}=\dfrac{3}{2}\overrightarrow{AD}&\Leftrightarrow&\overrightarrow{MK}-\overrightarrow{NK}=\dfrac{3}{2}\overrightarrow{AD}\\ \\&\Leftrightarrow&2k\overrightarrow{AD}-(k-1)\overrightarrow{AD}=\dfrac{3}{2}\overrightarrow{AD}\\ \\&\Leftrightarrow&2k\overrightarrow{AD}-(k-1)\overrightarrow{AD}-\dfrac{3}{2}\overrightarrow{AD}=\vec{0}\\ \\&\Leftrightarrow&\left(2k-k+1-\dfrac{3}{2}\right)\overrightarrow{AD}=\vec{0}\quad\text{or, }\ \overrightarrow{AD}\neq\vec{0}\\ \\&\Leftrightarrow&k-\dfrac{1}{2}=0\\ \\&\Leftrightarrow&k=\dfrac{1}{2}\end{array}$

D'où, $\overrightarrow{MN}=\dfrac{3}{2}\overrightarrow{AD}$ si, et seulement si, $k=\dfrac{1}{2}$

Exercice 52

Soit $ABCD$ un carré. On construit sur $[DC]$ et à l'intérieur du carré le triangle équilatéral $DCE.$
 
On construit sur $[BC]$ et à l'extérieur du carré le triangle équilatéral $BCF.$

 

 
1) Exprimons les vecteurs $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ en fonction des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}.$
 
Soit :
 
$\begin{array}{rcl}\overrightarrow{AE}&=&\overrightarrow{AG}+\overrightarrow{GE}\\ \\&=&\overrightarrow{AD}-\overrightarrow{GD}+\overrightarrow{GE}\end{array}$
 
Or, $\overrightarrow{GD}=\overrightarrow{EJ}$ et le triangle $DCE$ est équilatéral donc, $\overrightarrow{EJ}=\dfrac{\sqrt{3}}{2}\overrightarrow{AD}$
 
De plus, $\overrightarrow{GE}=\dfrac{1}{2}\overrightarrow{AB}$
 
Donc,
 
$\begin{array}{rcl}\overrightarrow{AE}&=&\overrightarrow{AD}-\overrightarrow{GD}+\overrightarrow{GE}\\ \\&=&\overrightarrow{AD}-\dfrac{\sqrt{3}}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\\ \\&=&\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2-\sqrt{3}}{2}\overrightarrow{AD}\end{array}$
 
D'où, $\boxed{\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2-\sqrt{3}}{2}\overrightarrow{AD}}$
 
Soit :
 
$\begin{array}{rcl}\overrightarrow{AF}&=&\overrightarrow{AH}+\overrightarrow{HF}\\ \\&=&\overrightarrow{AH}+\overrightarrow{HI}+\overrightarrow{IF}\end{array}$
 
Comme le triangle $BCF$ est équilatéral alors, $\overrightarrow{IF}=\dfrac{\sqrt{3}}{2}\overrightarrow{AB}$
 
De plus, $\overrightarrow{HI}=\overrightarrow{AB}\ $ et $\ \overrightarrow{AH}=\dfrac{1}{2}\overrightarrow{AD}$
 
Donc,
 
$\begin{array}{rcl}\overrightarrow{AF}&=&\overrightarrow{AH}+\overrightarrow{HI}+\overrightarrow{IF}\\ \\&=&\dfrac{1}{2}\overrightarrow{AD}+\overrightarrow{AB}+\dfrac{\sqrt{3}}{2}\overrightarrow{AB}\\ \\&=&\dfrac{1}{2}\overrightarrow{AD}+\dfrac{2+\sqrt{3}}{2}\overrightarrow{AB}\end{array}$
 
Ainsi, $\boxed{\overrightarrow{AF}=\dfrac{2+\sqrt{3}}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}}$
 
2)En déduisons que les points $A\;,\ E\;,\ F$ sont alignés.
 
On a :
 
$\begin{array}{rcl}\overrightarrow{AF}&=&\dfrac{2+\sqrt{3}}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\\ \\&=&(2+\sqrt{3})\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2-\sqrt{3}}{2}\overrightarrow{AD}\right)\\ \\&=&(2+\sqrt{3})\overrightarrow{AE}\end{array}$
 
Ainsi, $\overrightarrow{AF}=k\overrightarrow{AE}$ avec $k$ réel.
 
Par conséquent, les points $A\;,\ E\;,\ F$ sont alignés.
 
Autre méthode :
 
D'après le résultat de la question $1\;)$, on a :
 
$\overrightarrow{AF}=\dfrac{2+\sqrt{3}}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}$
 
$\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2-\sqrt{3}}{2}\overrightarrow{AD}$
 
Ainsi, dans le repère $\left(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AD}\right)$, les vecteurs $\overrightarrow{AF}\ $ et $\ \overrightarrow{AE}$ ont pour coordonnés :
 
$$\overrightarrow{AF}\begin{pmatrix}\dfrac{2+\sqrt{3}}{2}\\ \\\dfrac{1}{2}\end{pmatrix}\ \text{ et }\ \overrightarrow{AE}\begin{pmatrix}\dfrac{1}{2}\\ \\\dfrac{2-\sqrt{3}}{2}\end{pmatrix}$$
 
Alors, en calculant les rapports : $\dfrac{x_{_{\overrightarrow{AF}}}}{x_{_{\overrightarrow{AE}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{AF}}}}{y_{_{\overrightarrow{AE}}}}$, on obtient :
 
$\dfrac{x_{_{\overrightarrow{AF}}}}{x_{_{\overrightarrow{AE}}}}=\dfrac{\dfrac{2+\sqrt{3}}{2}}{\dfrac{1}{2}}=\dfrac{2+\sqrt{3}}{2}\times\dfrac{2}{1}=2+\sqrt{3}$
 
$\dfrac{y_{_{\overrightarrow{AF}}}}{y_{_{\overrightarrow{AE}}}}=\dfrac{\dfrac{1}{2}}{\dfrac{2-\sqrt{3}}{2}}=\dfrac{1}{2}\times\dfrac{2}{2-\sqrt{3}}=\dfrac{1}{2-\sqrt{3}}$
 
En rendant rationnel le dénominateur, on trouve :
 
$\begin{array}{lcl} \dfrac{y_{_{\overrightarrow{AF}}}}{y_{_{\overrightarrow{AE}}}}&=&\dfrac{1}{2-\sqrt{3}}\\\\&=&\dfrac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}\\\\&=&\dfrac{2+\sqrt{3}}{4-3}\\\\&=&\dfrac{2+\sqrt{3}}{1}\\\\&=&2+\sqrt{3}\end{array}$
 
On constate alors que :
$$\dfrac{x_{_{\overrightarrow{AF}}}}{x_{_{\overrightarrow{AE}}}}=\dfrac{y_{_{\overrightarrow{AF}}}}{y_{_{\overrightarrow{AE}}}}=2+\sqrt{3}$$
Ce qui entraine :
$$\overrightarrow{AF}=(2+\sqrt{3})\overrightarrow{AE}$$
D'où, les points $A\;,\ E\;,\ F$ sont alignés.
 
 
 


Auteur: 
Mouhamadou Ka & Diny Faye

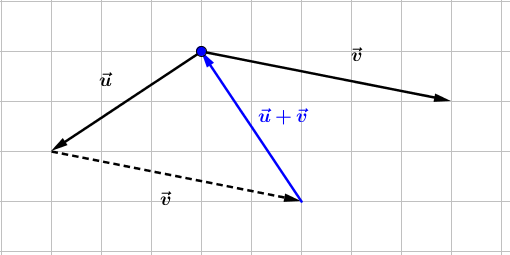
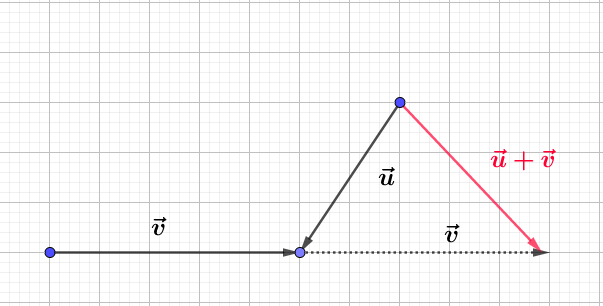
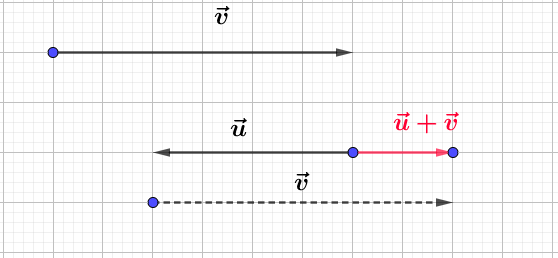
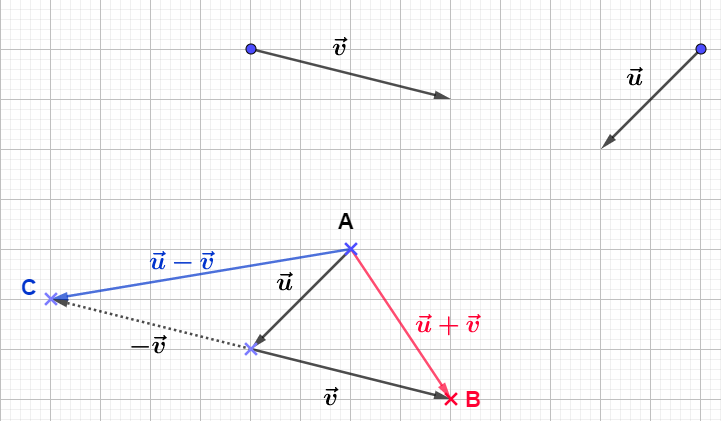
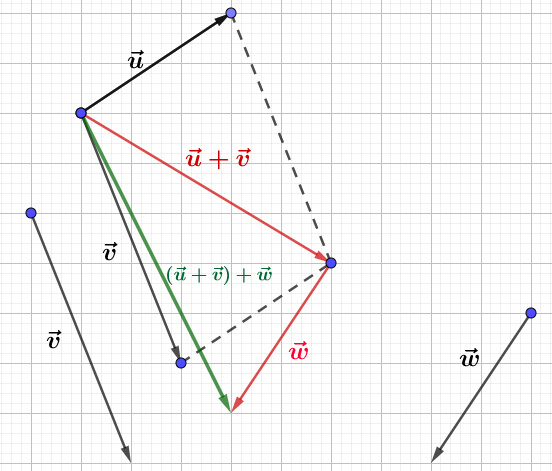
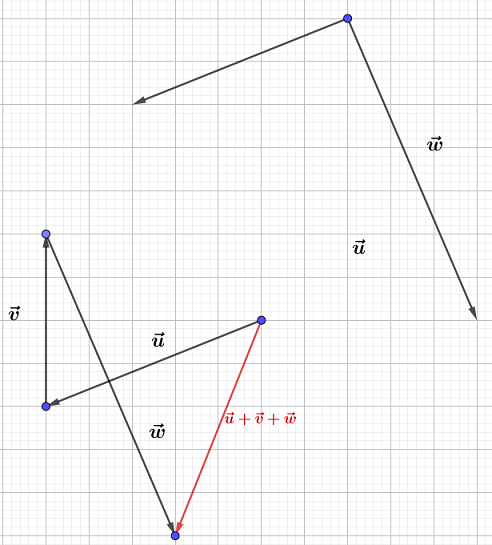
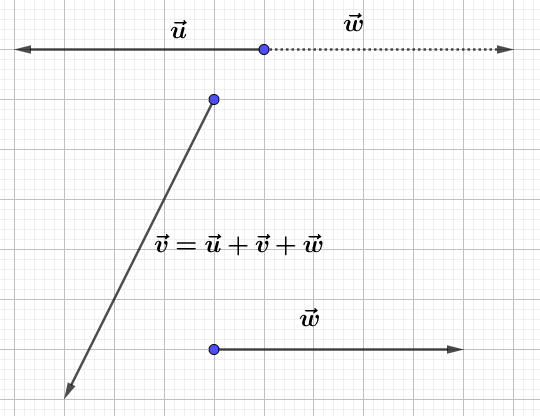
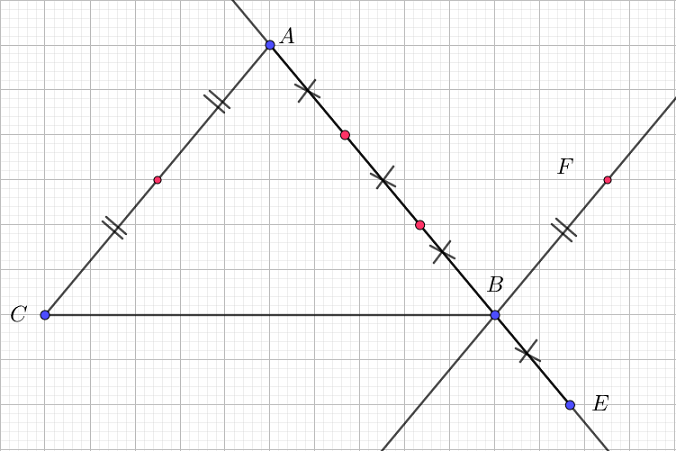
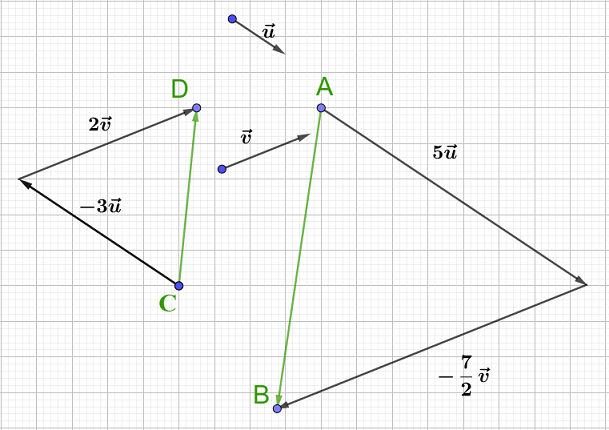
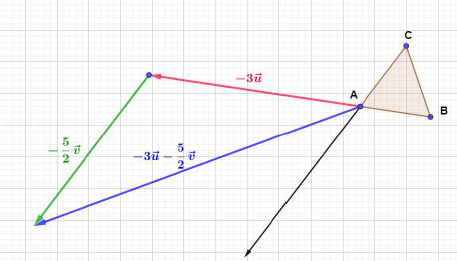
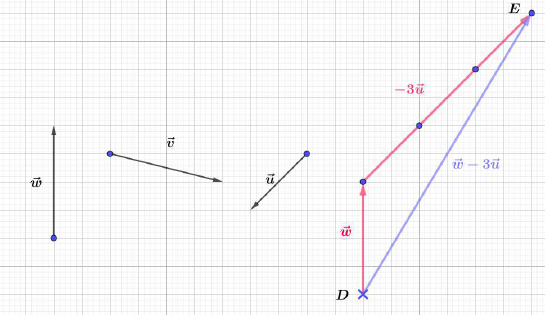
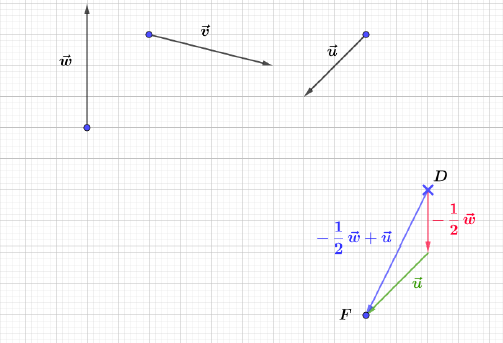
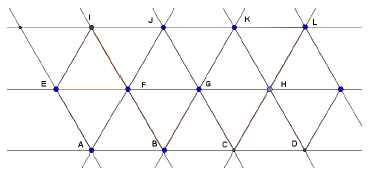
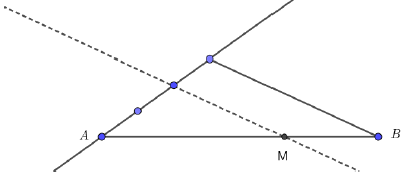
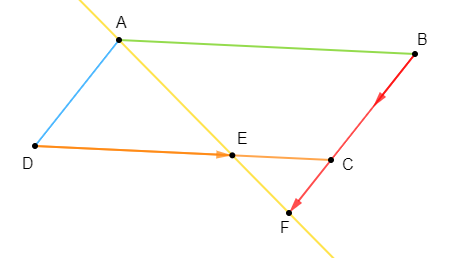
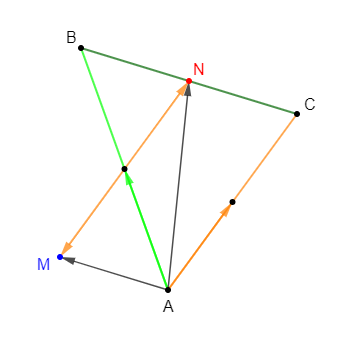
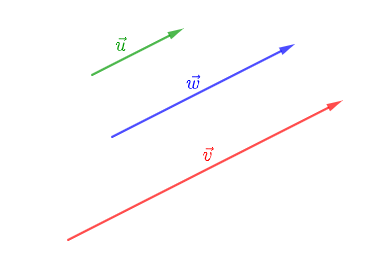
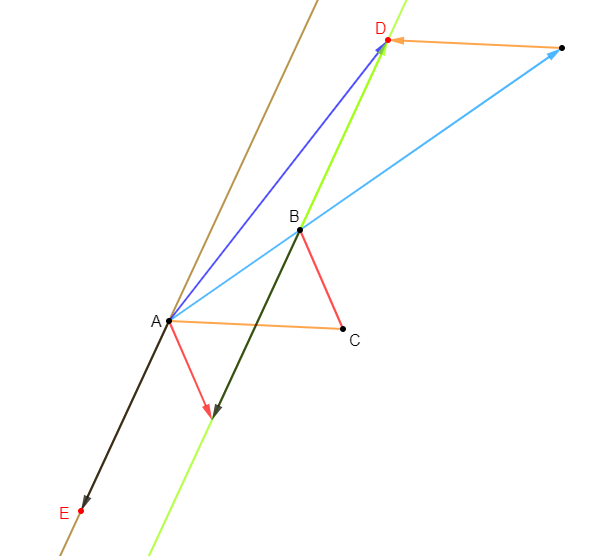
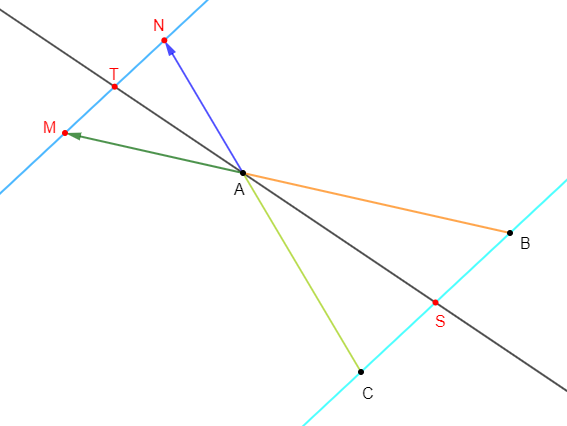
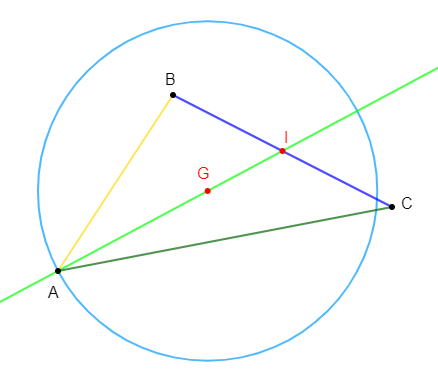
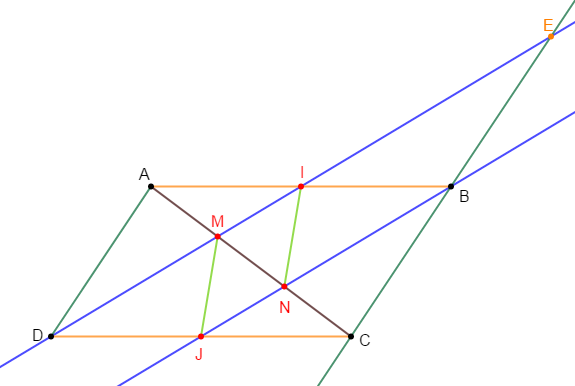
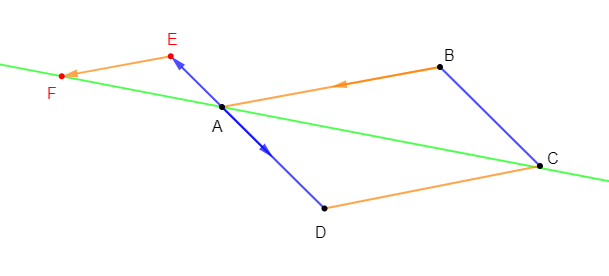
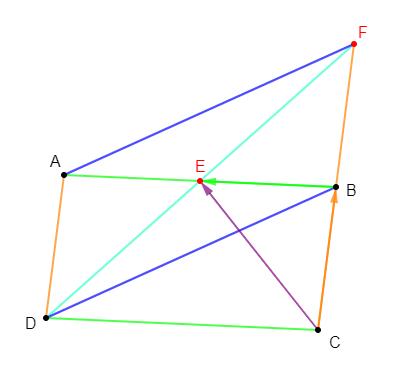
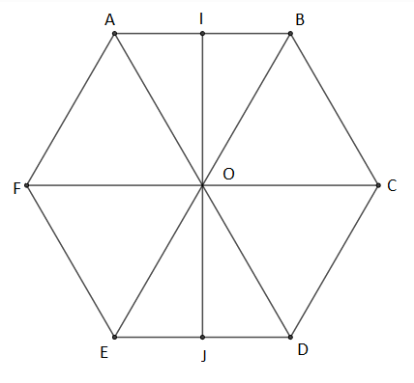
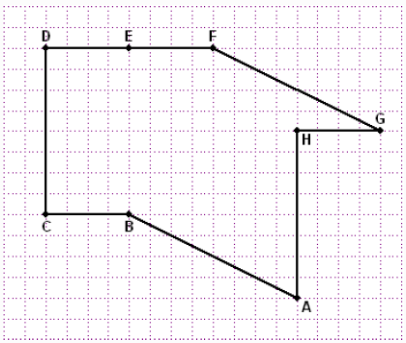
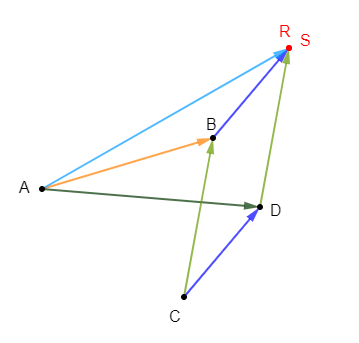
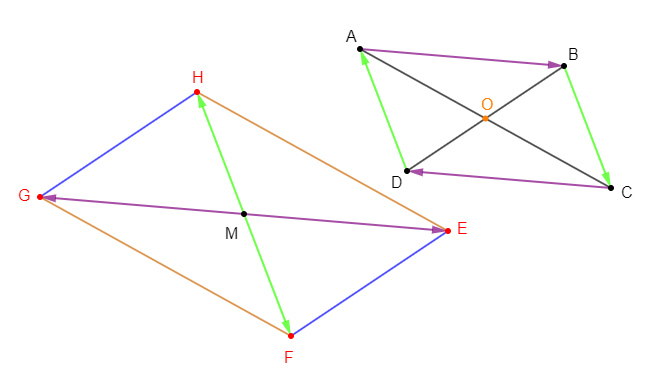
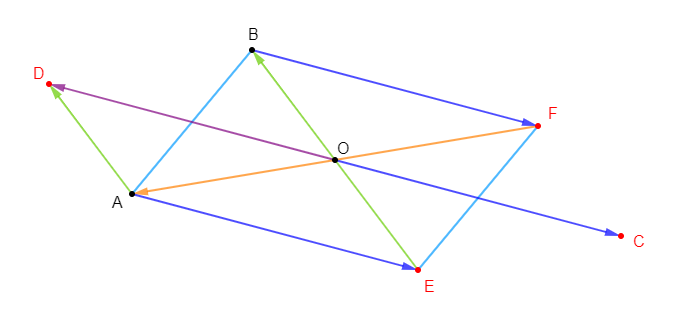
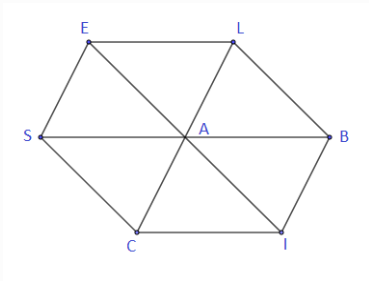
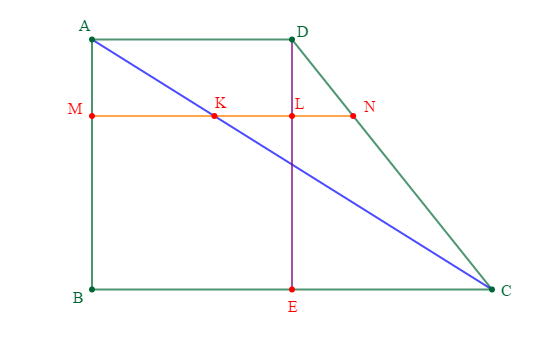
Commentaires

Anonyme (non vérifié)

mar, 01/29/2019 - 14:32

pertinant

Anonyme (non vérifié)

dim, 10/04/2020 - 20:40

Merci

Anonyme 23 (non vérifié)

mer, 12/16/2020 - 22:25

Bonjour. J aurais besoin de la correction de l exercice 59 svp. Merci

Anonyme (non vérifié)

sam, 01/09/2021 - 16:35

Bien fait

Anonyme (non vérifié)

mar, 01/12/2021 - 22:11

Intéressant.

Anonyme (non vérifié)

sam, 01/16/2021 - 14:05

j'aimerais bien voir la correction de l'exercice 60 et 61

Anonyme (non vérifié)

mer, 01/20/2021 - 22:03

Intéressant

Modou Diouf (non vérifié)

ven, 01/22/2021 - 00:04

J ai besoin de la correction de l exercice 59

HYACINTH A.B.MENDY (non vérifié)

mer, 01/27/2021 - 09:04

Plus d'exercices merci.

Thiam (non vérifié)

mer, 01/27/2021 - 17:42

Bonjour. J aurais besoin de la correction de l exercice 37 et 32 svp. Merci

sqmqne (non vérifié)

mer, 02/03/2021 - 22:19

la correction de l'exercice 25 svp

Moussa ba (non vérifié)

jeu, 12/30/2021 - 16:27

Bonjour, j'aimerais avoir la correction des exo 34 et 51 svp.

Anonyme (non vérifié)

sam, 11/19/2022 - 21:38

J'ai besoin de la correction de l'exercice 32

Ndeye awa niang (non vérifié)

dim, 11/20/2022 - 12:30

J'ai besoinde de la correction de l'exercice 33 et 48

maimouna diedhiou (non vérifié)

lun, 12/12/2022 - 23:27

j'ai besoin la correction de l'exo 13

Mame Diarra (non vérifié)

lun, 12/26/2022 - 14:16

Tout

Salamoun (non vérifié)

sam, 02/04/2023 - 14:01

de la correction de l exo 36 svp

Diallo (non vérifié)

mar, 12/12/2023 - 20:46

Correction de exercices 36

Salamoun (non vérifié)

sam, 02/04/2023 - 14:01

de la correction de l exo 36 svp

Salamoun (non vérifié)

sam, 02/04/2023 - 14:01

de la correction de l exo 36 svp

Anonyme (non vérifié)

lun, 09/25/2023 - 22:16

Cool

Anonyme (non vérifié)

lun, 09/25/2023 - 22:17

Cool

Ndeye Fatou diop (non vérifié)

jeu, 12/14/2023 - 21:26

J'ai besoin la correction de l'exercice 32

Ndeye Fatou diop (non vérifié)

jeu, 12/14/2023 - 21:26

J'ai besoin la correction de l'exercice 32

Ndeye Fatou diop (non vérifié)

jeu, 12/14/2023 - 21:26

J'ai besoin la correction de l'exercice 32

Anonyme (non vérifié)

mer, 11/20/2024 - 22:56

Je ne vois pas la correction de l'exercice 61

Ajouter un commentaire