2) Méthode analogue au 1) ; on trouve que ce vecteur est égal à $\overrightarrow{AB}+2\overrightarrow{AC}$
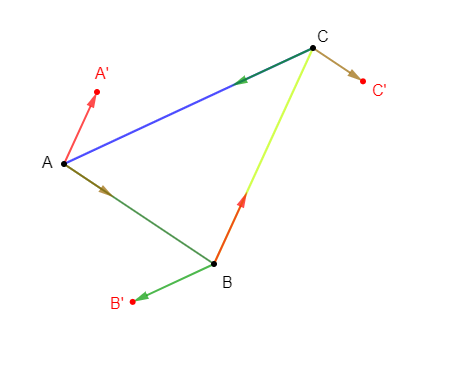
On donne un triangle $ABC$. On considère les points $A'\;,\ B'\ $ et $\ C'$ tels que : $$\overrightarrow{AA'}=\dfrac{1}{3}\overrightarrow{BC}\;,\quad \overrightarrow{BB'}=\dfrac{1}{3}\overrightarrow{CA}\;,\quad \overrightarrow{CC'}=\dfrac{1}{3}\overrightarrow{AB}$$
Démontrons que :
$$\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\vec{0}$$
Pour cela, calculons directement la somme vectorielle suivante :
$$\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}$$
Dans cette relation, remplaçons :
$\overrightarrow{AA'}$ par $\dfrac{1}{3}\overrightarrow{BC}$
$\overrightarrow{BB'}$ par $\dfrac{1}{3}\overrightarrow{CA}$
$\overrightarrow{CC'}$ par $\dfrac{1}{3}\overrightarrow{AB}$
On obtient alors :
$$\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\dfrac{1}{3}\overrightarrow{BC}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}$$
Puis, en appliquant la relation de Chasles et les propriétés du calcul vectoriel, on trouve :
$\begin{array}{rcl} \overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}&=&\dfrac{1}{3}\overrightarrow{BC}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\\\\&=&\dfrac{1}{3}\left(\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}\right)\\\\&=&\dfrac{1}{3}\left(\underbrace{\overrightarrow{BA}+\overrightarrow{AB}}_{=\vec{0}}\right)\\\\&=&\dfrac{1}{3}\times\vec{0}\\\\&=&\vec{0}\end{array}$
D'où, $\boxed{\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\vec{0}}$
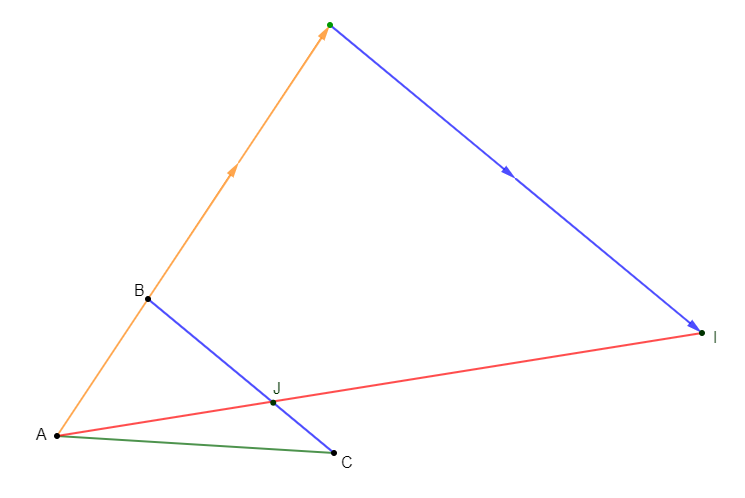
$ABC$ est un triangle. $J$ est le point tel que $\overrightarrow{BJ}=\dfrac{2}{3}\overrightarrow{BC}.$
1) Exprimons $\overrightarrow{AJ}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}.$
En effet, on a : $\overrightarrow{BJ}=\dfrac{2}{3}\overrightarrow{BC}.$
Donc, en introduisant le point $A$ dans le vecteur $\overrightarrow{BJ}$ par la relation de Chasles, on obtient :
$$\overrightarrow{BA}+\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{BC}$$
Par suite, en utilisant les propriétés du calcul vectoriel, on trouve :
$\begin{array}{rcl} \overrightarrow{BA}+\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{BC}&\Leftrightarrow&\overrightarrow{AJ}=-\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\\\\&\Leftrightarrow&\overrightarrow{AJ}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\end{array}$
Ainsi, $\boxed{\overrightarrow{AJ}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}}$
2) Soit $I$ le point tel que $\overrightarrow{AI}=3\overrightarrow{AB}+2\overrightarrow{BC}.$
Montrons que les points $A\;,\ I\ $ et $\ J$ sont alignés.
On a :
$\overrightarrow{AJ}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}$
$\overrightarrow{AI}=3\overrightarrow{AB}+2\overrightarrow{BC}$
Donc, dans la base $\left(\overrightarrow{AB}\;,\ \overrightarrow{BC}\right)$, les coordonnées des vecteurs $\overrightarrow{AJ}\ $ et $\ \overrightarrow{AI}$ sont données par :
$$\overrightarrow{AJ}\begin{pmatrix}1\\ \\\dfrac{2}{3}\end{pmatrix}\ \text{ et }\ \overrightarrow{AI}\begin{pmatrix}3\\ \\2\end{pmatrix}$$
Calculons alors les rapports : $\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AJ}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AJ}}}}$
On a :
$\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AJ}}}}=\dfrac{3}{1}=3$
$\dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AJ}}}}=\dfrac{2}{\dfrac{2}{3}}=\dfrac{2}{1}\times\dfrac{3}{2}=3$
On trouve une même valeur égale à $3.$
Ainsi, on a :
$$\left\lbrace\begin{array}{lcl}\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AJ}}}}&=&3\\ \\\dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AJ}}}}&=&3\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl} x_{_{\overrightarrow{AI}}}&=&3\times x_{_{\overrightarrow{AJ}}}\\ \\y_{_{\overrightarrow{AI}}}&=&3\times y_{_{\overrightarrow{AJ}}}\end{array}\right.$$
Ce qui signifie que, $\overrightarrow{AI}=3\overrightarrow{AJ}$
Par conséquent, les points $A\;,\ I\ $ et $\ J$ sont alignés.
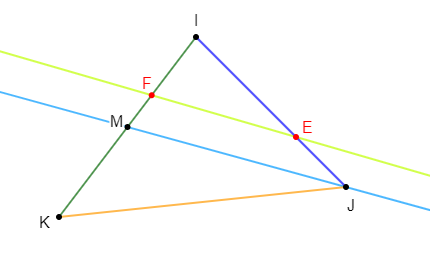
$IJK$ est un triangle. Les points $E\ $ et $\ F$ sont tels que :
$$\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{IJ}\ \text{ et }\ \overrightarrow{IF}=\dfrac{1}{3}\overrightarrow{IK}$$
$M$ est le milieu du segment $[IK].$
1) Exprimons $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ en fonction de $\overrightarrow{IJ}\ $ et $\ \overrightarrow{IK}$
On a : $\overrightarrow{IF}=\dfrac{1}{3}\overrightarrow{IK}$
Alors, introduisons le point $E$ dans le vecteur $\overrightarrow{IF}$ en utilisant la relation de Chasles.
On obtient :
$$\overrightarrow{IE}+\overrightarrow{EF}=\dfrac{1}{3}\overrightarrow{IK}$$
Or, on sait que : $\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{IJ}$
Donc, en remplaçant $\overrightarrow{IE}$ par $\dfrac{2}{3}\overrightarrow{IJ}$, on trouve :
$$\dfrac{2}{3}\overrightarrow{IJ}+\overrightarrow{EF}=\dfrac{1}{3}\overrightarrow{IK}$$
D'où, $\boxed{\overrightarrow{EF}=-\dfrac{2}{3}\overrightarrow{IJ}+\dfrac{1}{3}\overrightarrow{IK}}$
Par ailleurs, en utilisant la relation de Chasles, on introduit le point $M$ dans le vecteur $\overrightarrow{IJ}.$
On obtient alors :
$$\overrightarrow{IJ}=\overrightarrow{IM}+\overrightarrow{MJ}$$
Ainsi,
$$-\overrightarrow{MJ}=-\overrightarrow{IJ}+\overrightarrow{IM}$$
Or, on sait que $M$ est le milieu de $[IK].$
Ce qui signifie que : $\overrightarrow{IM}=\dfrac{1}{2}\overrightarrow{IK}$
Donc, en remplaçant $\overrightarrow{IM}$ par $\dfrac{1}{2}\overrightarrow{IK}$, on trouve :
$$-\overrightarrow{MJ}=-\overrightarrow{IJ}+\dfrac{1}{2}\overrightarrow{IK}$$
D'où, $\boxed{\overrightarrow{JM}=-\overrightarrow{IJ}+\dfrac{1}{2}\overrightarrow{IK}}$
2) Montrons que les droites $(EF)\ $ et $\ (JM)$ sont parallèles.
En effet, les droites $(EF)\ $ et $\ (JM)$ sont parallèles si, et seulement si, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ sont colinéaires.
Or, $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ sont colinéaires si, et seulement si, il existe un nombre réel $k$ non nul, tel que :
$$\overrightarrow{EF}=k\overrightarrow{JM}$$
D'après les résultats de la question $1\;)$, on a :
$\begin{array}{rcl}\overrightarrow{EF}&=&-\dfrac{2}{3}\overrightarrow{IJ}+\dfrac{1}{3}\overrightarrow{IK}\\\\&=&\dfrac{2}{3}\left(\underbrace{-\overrightarrow{IJ}+\dfrac{1}{2}\overrightarrow{IK}}_{=\overrightarrow{JM}}\right)\\\\&=&\dfrac{2}{3}\overrightarrow{JM}\end{array}$
Ainsi, $\boxed{\overrightarrow{EF}=\dfrac{2}{3}\overrightarrow{JM}}$
D'où, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ sont colinéaires.
Et par conséquent, les droites $(EF)\ $ et $\ (JM)$ sont parallèles.
Autre méthode :
En effet, d'après les résultats de la question $1\;)$, on a :
$\overrightarrow{EF}=-\dfrac{2}{3}\overrightarrow{IJ}+\dfrac{1}{3}\overrightarrow{IK}$
$\overrightarrow{JM}=-\overrightarrow{IJ}+\dfrac{1}{2}\overrightarrow{IK}$
Ainsi, dans la base $\left(\overrightarrow{IJ}\;,\ \overrightarrow{IK}\right)$, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ ont pour coordonnées :
$$\overrightarrow{EF}\begin{pmatrix}-\dfrac{2}{3}\\ \\\dfrac{1}{3}\end{pmatrix}\ \text{ et }\ \overrightarrow{JM}\begin{pmatrix}-1\\ \\\dfrac{1}{2}\end{pmatrix}$$
Alors, en appliquant la condition de colinéarité sur ces deux vecteurs, on obtient :
$$-\dfrac{2}{3}\times\dfrac{1}{2}-\dfrac{1}{3}\times(-1)=-\dfrac{1}{3}+\dfrac{1}{3}=0$$
Donc, les coordonnées des vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ vérifient la condition de colinéarité.
Ce qui signifie que ces deux vecteurs sont colinéaires.
Par conséquent, les droites $(EF)\ $ et $\ (JM)$ sont parallèles.
Nous pouvons aussi utiliser les rapports des coordonnées pour vérifier la colinéarité.
Alors, calculons les rapports : $\dfrac{x_{_{\overrightarrow{EF}}}}{x_{_{\overrightarrow{JM}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{EF}}}}{y_{_{\overrightarrow{JM}}}}$
On a :
$\dfrac{x_{_{\overrightarrow{EF}}}}{x_{_{\overrightarrow{JM}}}}=\dfrac{-\dfrac{2}{3}}{-1}=\dfrac{2}{3}$
$\dfrac{y_{_{\overrightarrow{EF}}}}{y_{_{\overrightarrow{JM}}}}=\dfrac{\dfrac{1}{3}}{\dfrac{1}{2}}=\dfrac{1}{3}\times\dfrac{2}{1}=\dfrac{2}{3}$
Ainsi,
$$\dfrac{x_{_{\overrightarrow{EF}}}}{x_{_{\overrightarrow{JM}}}}=\dfrac{y_{_{\overrightarrow{EF}}}}{y_{_{\overrightarrow{JM}}}}=\dfrac{2}{3}$$
D'où, $\boxed{\overrightarrow{EF}=\dfrac{2}{3}\overrightarrow{JM}}$
Ce qui signifie que les vecteurs $\overrightarrow{EF}\ $ et $\ \dfrac{2}{3}\overrightarrow{JM}$ sont colinéaires.
Par conséquent, les droites $(EF)\ $ et $\ (JM)$ sont parallèles.
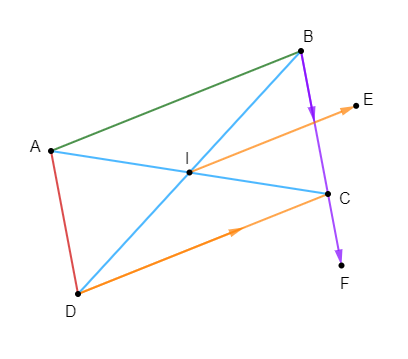
$ABCD$ est un parallélogramme de centre $I.$ Les points $E\ $ et $\ F$ sont tels que :
$$\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{DC}\ \text{ et }\ \overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$$
Exprimons $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$
On a : $\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{DC}$
En utilisant la relation de Chasles, introduisons le point $A$ dans le vecteur $\overrightarrow{IE}.$
On obtient :
$$\overrightarrow{IA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}$$
Comme $ABCD$ est un parallélogramme de centre $I$ alors, $I$ est le milieu de la diagonale $[CA].$
D'où, $\overrightarrow{IA}=\dfrac{1}{2}\overrightarrow{CA}$
Par ailleurs, en utilisant encore la relation de Chasles, on a :
$$\overrightarrow{CA}=\overrightarrow{CD}+\overrightarrow{DA}$$
Par suite,
$$\overrightarrow{IA}=\dfrac{1}{2}\left(\overrightarrow{CD}+\overrightarrow{DA}\right)$$
Donc, en remplaçant $\overrightarrow{IA}$ par son expression, on obtient :
$\begin{array}{rcl}\overrightarrow{IA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}&\Leftrightarrow&\dfrac{1}{2}\left(\overrightarrow{CD}+\overrightarrow{DA}\right)+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}\\\\&\Leftrightarrow&\dfrac{1}{2}\overrightarrow{CD}+\dfrac{1}{2}\overrightarrow{DA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}-\dfrac{1}{2}\overrightarrow{CD}-\dfrac{1}{2}\overrightarrow{DA}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}+\dfrac{1}{2}\overrightarrow{DC}+\dfrac{1}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{7}{6}\overrightarrow{DC}+\dfrac{1}{2}\overrightarrow{AD}\end{array}$
Comme $ABCD$ est un parallélogramme alors,
$$\overrightarrow{DC}=\overrightarrow{AB}$$
D'où, en remplaçant $\overrightarrow{DC}$ par $\overrightarrow{AB}$, on trouve : $\boxed{\overrightarrow{AE}=\dfrac{7}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}}$
Soit : $\overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$
Alors, introduisons le point $A$ dans le vecteur $\overrightarrow{BF}$, par la relation de Chasles.
On obtient :
$$\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{BC}$$
Comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{BC}=\overrightarrow{AD}$$
Ainsi, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{AD}$, on trouve :
$\begin{array}{rcl}\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{BC}&\Leftrightarrow&\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AF}=-\overrightarrow{BA}+\dfrac{3}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}\end{array}$
D'où, $\boxed{\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}}$
$ABC$ est un triangle,$\alpha$ un nombre réel. On considère les points $P\;,\ Q\ $ et $\ R$ définis par : $$\overrightarrow{AP}=\alpha\overrightarrow{AB}\;,\quad \overrightarrow{CQ}=\alpha\overrightarrow{CA}\;,\quad \overrightarrow{CR}=\alpha\overrightarrow{BC}$$
1) Exprimons $\overrightarrow{PQ}\ $ et $\ \overrightarrow{PR}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$
Soit : $\overrightarrow{CQ}=\alpha\overrightarrow{CA}$
Alors, dans le vecteur $\overrightarrow{CQ}$ introduisons le point $P$ en utilisant la relation de Chasles.
On obtient :
$$\overrightarrow{CP}+\overrightarrow{PQ}=\alpha\overrightarrow{CA}$$
En utilisant le même procédé, introduisons le point $A$ dans le vecteur $\overrightarrow{CP}.$
Cela donne alors :
$$\overrightarrow{CA}+\overrightarrow{AP}+\overrightarrow{PQ}=\alpha\overrightarrow{CA}$$
Or, on sait que : $\overrightarrow{AP}=\alpha\overrightarrow{AB}$
Donc, en remplaçant $\overrightarrow{AP}$ par $\alpha\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :
$\begin{array}{rcl}\overrightarrow{CA}+\overrightarrow{AP}+\overrightarrow{PQ}=\alpha\overrightarrow{CA}&\Leftrightarrow&\overrightarrow{CA}+\alpha\overrightarrow{AB}+\overrightarrow{PQ}=\alpha\overrightarrow{CA}\\\\&\Leftrightarrow&\overrightarrow{PQ}=-\alpha\overrightarrow{AB}-\overrightarrow{CA}+\alpha\overrightarrow{CA}\\\\&\Leftrightarrow&\overrightarrow{PQ}=-\alpha\overrightarrow{AB}+\overrightarrow{AC}-\alpha\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{PQ}=-\alpha\overrightarrow{AB}+(1-\alpha)\overrightarrow{AC}\end{array}$
D'où, $\boxed{\overrightarrow{PQ}=-\alpha\overrightarrow{AB}+(1-\alpha)\overrightarrow{AC}}$
Soit : $\overrightarrow{CR}=\alpha\overrightarrow{BC}$
Alors, de la même manière, utilisons la relation de Chasles pour introduire le point $P$ dans le vecteur $\overrightarrow{CR}.$
On obtient :
$$\overrightarrow{CP}+\overrightarrow{PR}=\alpha\overrightarrow{BC}$$
En utilisant le même procédé, introduisons le point $A$ dans le vecteur $\overrightarrow{CP}$ puis, dans le vecteur $\overrightarrow{BC}.$
Ce qui donne :
$$\overrightarrow{CA}+\overrightarrow{AP}+\overrightarrow{PR}=\alpha\left(\overrightarrow{BA}+\overrightarrow{AC}\right)$$
Par ailleurs, on sait que : $\overrightarrow{AP}=\alpha\overrightarrow{AB}$
Alors, en remplaçant $\overrightarrow{AP}$ par $\alpha\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :
$\begin{array}{rcl}\overrightarrow{CA}+\overrightarrow{AP}+\overrightarrow{PR}=\alpha\left(\overrightarrow{BA}+\overrightarrow{AC}\right)&\Leftrightarrow&\overrightarrow{CA}+\alpha\overrightarrow{AB}+\overrightarrow{PR}=\alpha\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\\\\&\Leftrightarrow&\overrightarrow{PR}=-\alpha\overrightarrow{AB}-\overrightarrow{CA}+\alpha\overrightarrow{BA}+\alpha\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{PR}=-\alpha\overrightarrow{AB}-\alpha\overrightarrow{AB}+\overrightarrow{AC}+\alpha\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{PR}=-2\alpha\overrightarrow{AB}+(1+\alpha)\overrightarrow{AC}\end{array}$
Par conséquent, $\boxed{\overrightarrow{PR}=-2\alpha\overrightarrow{AB}+(1+\alpha)\overrightarrow{AC}}$
2) Vérifions s'il existe des valeurs de $\alpha$ pour lesquels les points $P\;,\ Q\ $ et $\ R$ sont alignés.
En effet, d'après les résultats de la question $1\;)$, on a :
$\overrightarrow{PQ}=-\alpha\overrightarrow{AB}+(1-\alpha)\overrightarrow{AC}$
$\overrightarrow{PR}=-2\alpha\overrightarrow{AB}+(1+\alpha)\overrightarrow{AC}$
Donc, dans la base $\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$, les vecteurs $\overrightarrow{PQ}\ $ et $\ \overrightarrow{PR}$ ont pour coordonnées :
$$\overrightarrow{PQ}\begin{pmatrix}-\alpha\\ \\(1-\alpha)\end{pmatrix}\ \text{ et }\ \overrightarrow{PR}\begin{pmatrix}-2\alpha\\ \\(1+\alpha)\end{pmatrix}$$
Or, on sait que les points $P\;,\ Q\ $ et $\ R$ sont alignés si, et seulement si, les coordonnées des vecteurs $\overrightarrow{PQ}\ $ et $\ \overrightarrow{PR}$ vérifient :
$$\dfrac{x_{_{\overrightarrow{PQ}}}}{x_{_{\overrightarrow{PR}}}}=\dfrac{y_{_{\overrightarrow{PQ}}}}{y_{_{\overrightarrow{PR}}}}=\text{Constante}$$
Soit alors :
$\begin{array}{rcl}\dfrac{x_{_{\overrightarrow{PQ}}}}{x_{_{\overrightarrow{PR}}}}=\dfrac{y_{_{\overrightarrow{PQ}}}}{y_{_{\overrightarrow{PR}}}}&\Leftrightarrow&\dfrac{-\alpha}{-2\alpha}=\dfrac{(1-\alpha)}{(1+\alpha)}\\\\&\Leftrightarrow&\dfrac{1}{2}=\dfrac{(1-\alpha)}{(1+\alpha)}\\\\&\Leftrightarrow&1(1+\alpha)=2(1-\alpha)\\\\&\Leftrightarrow&1+\alpha=2-2\alpha\\\\&\Leftrightarrow&\alpha+2\alpha=2-1\\\\&\Leftrightarrow&3\alpha=1\\\\&\Leftrightarrow&\alpha=\dfrac{1}{3}\end{array}$
D'où, $\boxed{\alpha=\dfrac{1}{3}}$
Ainsi, les points $P\;,\ Q\ $ et $\ R$ sont alignés lorsque $\alpha=\dfrac{1}{3}.$
$A\;,\ B\ $ et $\ C$ sont trois points non alignés. Les points $D\;,\ E\ $ et $\ F$ sont définis par les égalités de vecteurs suivants :
$$\overrightarrow{AD}=3\overrightarrow{AB}\;,\quad \overrightarrow{AE}=\dfrac{3}{2}\overrightarrow{AC}\;,\quad \overrightarrow{BF}=2\overrightarrow{BC}$$
1) Exprimons $\overrightarrow{DE}\ $ et $\ \overrightarrow{DF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$
Soit : $\overrightarrow{AE}=\dfrac{3}{2}\overrightarrow{AC}$
Alors, en introduisant le point $D$ dans le vecteur $\overrightarrow{AE}$, par la relation de Chasles, on obtient :
$$\overrightarrow{AD}+\overrightarrow{DE}=\dfrac{3}{2}\overrightarrow{AC}$$
Or, on sait que : $\overrightarrow{AD}=3\overrightarrow{AB}$
Donc, en remplaçant $\overrightarrow{AD}$ par $3\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :
$\begin{array}{rcl}\overrightarrow{AD}+\overrightarrow{DE}=\dfrac{3}{2}\overrightarrow{AC}&\Leftrightarrow&3\overrightarrow{AB}+\overrightarrow{DE}=\dfrac{3}{2}\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{DE}=-3\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\end{array}$
D'où, $\boxed{\overrightarrow{DE}=-3\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}}$
Soit : $\overrightarrow{BF}=2\overrightarrow{BC}$
Alors, de la même manière, en utilisant la relation de Chasles pour introduire le point $D$ dans le vecteur $\overrightarrow{BF}$, on obtient :
$$\overrightarrow{BD}+\overrightarrow{DF}=2\overrightarrow{BC}$$
Ensuite, utilisons le même procédé pour introduire le point $A$ dans le vecteur $\overrightarrow{BD}$ puis, dans le vecteur $\overrightarrow{BC}.$
Cela donne alors :
$$\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DF}=2\left(\overrightarrow{BA}+\overrightarrow{AC}\right)$$
Comme $\overrightarrow{AD}=3\overrightarrow{AB}$ alors, en remplaçant $\overrightarrow{AD}$ par $3\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :
$\begin{array}{rcl}\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DF}=2\left(\overrightarrow{BA}+\overrightarrow{AC}\right)&\Leftrightarrow&\overrightarrow{BA}+3\overrightarrow{AB}+\overrightarrow{DF}=2\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\\\\&\Leftrightarrow&\overrightarrow{DF}=-3\overrightarrow{AB}-\overrightarrow{BA}+2\overrightarrow{BA}+2\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{DF}=-3\overrightarrow{AB}+\overrightarrow{AB}-2\overrightarrow{AB}+2\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{DF}=-4\overrightarrow{AB}+2\overrightarrow{AC}\end{array}$
Par conséquent, $\boxed{\overrightarrow{DF}=-4\overrightarrow{AB}+2\overrightarrow{AC}}$
2) Montrons que les points $D\;,\ E\ $ et $\ F$ sont alignés.
En effet, les points $D\;,\ E\ $ et $\ F$ sont alignés si, et seulement si, il existe un nombre réel $k$ non nul tel que :
$$\overrightarrow{DE}=k\overrightarrow{DF}$$
D'après les résultats de la question $1\;)$, on a :
$\overrightarrow{DE}=-3\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}$
$\overrightarrow{DF}=-4\overrightarrow{AB}+2\overrightarrow{AC}$
Ainsi, dans la base $\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$, les coordonnées des vecteurs $\overrightarrow{DE}\ $ et $\ \overrightarrow{DF}$ sont données par :
$$\overrightarrow{DE}\begin{pmatrix}-3\\ \\\dfrac{3}{2}\end{pmatrix}\ \text{ et }\ \overrightarrow{DF}\begin{pmatrix}-4\\ \\2\end{pmatrix}$$
Calculons alors les rapports : $\dfrac{x_{_{\overrightarrow{DE}}}}{x_{_{\overrightarrow{DF}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{DE}}}}{y_{_{\overrightarrow{DF}}}}$
On a :
$\dfrac{x_{_{\overrightarrow{DE}}}}{x_{_{\overrightarrow{DF}}}}=\dfrac{-3}{-4}=\dfrac{3}{4}$
$\dfrac{y_{_{\overrightarrow{DE}}}}{y_{_{\overrightarrow{DF}}}}=\dfrac{\dfrac{3}{2}}{2}=\dfrac{3}{2}\times\dfrac{1}{2}=\dfrac{3}{4}$
On constate que l'on trouve une même valeur égale à $\dfrac{3}{4}.$
Ainsi, on peut écrire :
$$\left\lbrace\begin{array}{lcl}\dfrac{x_{_{\overrightarrow{DE}}}}{x_{_{\overrightarrow{DF}}}}&=&\dfrac{3}{4}\\ \\\dfrac{y_{_{\overrightarrow{DE}}}}{y_{_{\overrightarrow{DF}}}}&=&\dfrac{3}{4}\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl} x_{_{\overrightarrow{DE}}}&=&\dfrac{3}{4}\times x_{_{\overrightarrow{DF}}}\\ \\y_{_{\overrightarrow{DE}}}&=&\dfrac{3}{4}\times y_{_{\overrightarrow{DF}}}\end{array}\right.$$
Par conséquent, $\boxed{\overrightarrow{DE}=\dfrac{3}{4}\overrightarrow{DF}}$
Ce qui montre que les points $D\;,\ E\ $ et $\ F$ sont alignés.
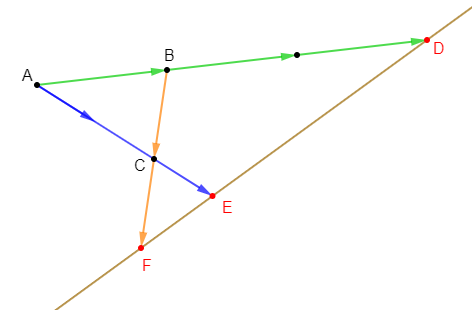
Le segment $[AB]$ est divisé en $6$ parties de même longueur. Complétons les relations suivantes par la lettre ou le nombre qui convient.
1) $EC=2EF$
2) $CE=EG$
3) $AB=AB$
4) $CE=\dfrac{1}{3}AB$
5) $AD=BF$
6) $DE=\dfrac{1}{2}BF$
$ABCD$ est un parallélogramme. Les points $E\ $ et $\ F$ sont tels que :
$$\overrightarrow{DE}=\dfrac{2}{3}\overrightarrow{DC}\ \text{ et }\ \overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$$
1) Exprimons $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$
Soit : $\overrightarrow{DE}=\dfrac{2}{3}\overrightarrow{DC}$
Alors, par la relation de Chasles, en introduisant le point $A$ dans le vecteur $\overrightarrow{DE}$, on obtient :
$$\overrightarrow{DA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}$$
Par ailleurs, comme $ABCD$ est un parallélogramme alors,
$$\overrightarrow{DC}=\overrightarrow{AB}$$
Ainsi, en remplaçant $\overrightarrow{DC}$ par $\overrightarrow{AB}$, on trouve :
$\begin{array}{rcl}\overrightarrow{DA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{DC}&\Leftrightarrow&\overrightarrow{DA}+\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}-\overrightarrow{DA}\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}\end{array}$
D'où, $\boxed{\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}}$
Soit : $\overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$
Alors, introduisons le point $A$ dans le vecteur $\overrightarrow{BF}$, par la relation de Chasles.
On obtient :
$$\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{BC}$$
Comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{BC}=\overrightarrow{AD}$$
Ainsi, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{AD}$, on trouve :
$\begin{array}{rcl}\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{BC}&\Leftrightarrow&\overrightarrow{BA}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AF}=-\overrightarrow{BA}+\dfrac{3}{2}\overrightarrow{AD}\\\\&\Leftrightarrow&\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}\end{array}$
D'où, $\boxed{\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}}$
2) Montrons que les points $A\;,\ E\ $ et $\ F$ sont alignés.
En effet, les points $A\;,\ E\ $ et $\ F$ sont alignés si, et seulement si, il existe un nombre réel $k$ non nul tel que :
$$\overrightarrow{AE}=k\overrightarrow{AF}$$
D'après les résultats de la question $1\;)$, on a :
$\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}$
$\overrightarrow{AF}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}$
Ainsi, dans le repère $\left(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AD}\right)$, les vecteurs $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ ont pour coordonnées :
$$\overrightarrow{AE}\begin{pmatrix}\dfrac{2}{3}\\ \\1\end{pmatrix}\ \text{ et }\ \overrightarrow{AF}\begin{pmatrix}1\\ \\\dfrac{3}{2}\end{pmatrix}$$
Alors, en calculant alors les rapports : $\dfrac{x_{_{\overrightarrow{AE}}}}{x_{_{\overrightarrow{AF}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{AE}}}}{y_{_{\overrightarrow{AF}}}}$, on trouve :
$\dfrac{x_{_{\overrightarrow{AE}}}}{x_{_{\overrightarrow{AF}}}}=\dfrac{\dfrac{2}{3}}{1}=\dfrac{2}{3}$
$\dfrac{y_{_{\overrightarrow{AE}}}}{y_{_{\overrightarrow{AF}}}}=\dfrac{1}{\dfrac{3}{2}}=1\times\dfrac{2}{3}=\dfrac{2}{3}$
Ainsi, nous obtenons une même valeur égale à $\dfrac{2}{3}.$
Par suite, on peut écrire :
$$\left\lbrace\begin{array}{lcl}\dfrac{x_{_{\overrightarrow{AE}}}}{x_{_{\overrightarrow{AF}}}}&=&\dfrac{2}{3}\\ \\\dfrac{y_{_{\overrightarrow{AE}}}}{y_{_{\overrightarrow{AF}}}}&=&\dfrac{2}{3}\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl} x_{_{\overrightarrow{AE}}}&=&\dfrac{2}{3}\times x_{_{\overrightarrow{AF}}}\\ \\y_{_{\overrightarrow{AE}}}&=&\dfrac{2}{3}\times y_{_{\overrightarrow{AF}}}\end{array}\right.$$
Par conséquent, $\boxed{\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AF}}$
Ce qui montre que les points $A\;,\ E\ $ et $\ F$ sont alignés.
Autre méthode :
On a :
$\begin{array}{rcl}\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\left(\underbrace{\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AD}}_{=\overrightarrow{AF}}\right)\\\\&\Leftrightarrow&\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AF}\end{array}$
D'où, $\boxed{\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AF}}$
Par conséquent, les points $A\;,\ E\ $ et $\ F$ sont alignés.
Soit $ABC$ un triangle quelconque.
1) Construisons les points $D\ $ et $\ E$ tels que $\overrightarrow{AD}=\overrightarrow{BC}\;,\quad\overrightarrow{CE}=2\overrightarrow{BA}$
2) Démontrons que $D$ est le milieu de $[CE]$
En effet, on a :
$$\overrightarrow{CE}=2\overrightarrow{BA}$$
Par ailleurs, on sait que :
$$\overrightarrow{AD}=\overrightarrow{BC}$$
Ce qui signifie que $ADCB$ est un parallélogramme.
Par conséquent,
$$\overrightarrow{BA}=\overrightarrow{CD}$$
Ainsi, dans l'expression de $\overrightarrow{CE}$, en remplaçant $\overrightarrow{BA}$ par $\overrightarrow{CD}$, on obtient :
$$\boxed{\overrightarrow{CE}=2\overrightarrow{CD}}$$
Ce qui démontre que $D$ est le milieu de $[CE]$
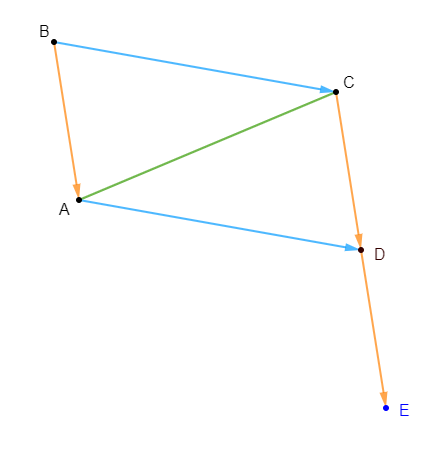
Soit $ABC$ un triangle. Construisons les points $M\ $ et $\ N$ tels que : $$\left\lbrace\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}&=&\overrightarrow{AB} \\\\ \overrightarrow{AN}-\overrightarrow{AM}&=&\overrightarrow{AC}\end{array}\right.$$
Pour cela, nous allons d'abord exprimer les vecteurs $\overrightarrow{AN}\ $ et $\ \overrightarrow{AM}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$
En effet, résolvons ce système en additionnant membre à membre les deux égalités.
On obtient :
$\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}+\overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}&\Leftrightarrow&2\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{AN}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{2}\end{array}$
D'où, $\boxed{\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}}$
En remplaçant $\overrightarrow{AN}$ par son expression, dans la première égalité, on obtient :
$\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}=\overrightarrow{AB}&\Leftrightarrow&\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}+\overrightarrow{AM}=\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{AM}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\end{array}$
D'où, $\boxed{\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}}$
Construisons trois vecteurs $\vec{u}\;,\ \vec{v}\ $ et $\ \vec{w}$ tels que :
$$\left\lbrace\begin{array}{rcl}\vec{u}+\vec{v}-2\vec{w}&=&\vec{0} \\ \vec{u}-\vec{v}+\vec{w}&=&\vec{0}\end{array}\right.$$
Pour cela, nous allons d'abord exprimer $\vec{u}\ $ et $\ \vec{v}$ en fonction de $\vec{w}.$
En additionnant membre à membre les deux égalités du système, on obtient :
$\begin{array}{rcl}\vec{u}+\vec{v}-2\vec{w}+\vec{u}-\vec{v}+\vec{w}=\vec{0}+\vec{0}&\Leftrightarrow&2\vec{u}-\vec{w}=\vec{0}\\\\&\Leftrightarrow&2\vec{u}=\vec{w}\\\\&\Leftrightarrow&\vec{u}=\dfrac{1}{2}\vec{w}\end{array}$
Donc, $\boxed{\vec{u}=\dfrac{1}{2}\vec{w}}$
En remplaçant $\vec{u}$ par son expression, dans la première égalité, on obtient :
$\begin{array}{rcl}\vec{u}+\vec{v}-2\vec{w}=\vec{0}&\Leftrightarrow&\dfrac{1}{2}\vec{w}+\vec{v}-2\vec{w}=\vec{0}\\\\&\Leftrightarrow&\vec{v}-\dfrac{3}{2}\vec{w}=\vec{0}\\\\&\Leftrightarrow&\vec{v}=\dfrac{3}{2}\vec{w}\end{array}$
D'où, $\boxed{\vec{v}=\dfrac{3}{2}\vec{w}}$
Ainsi, on place d'abord $\vec{w}$ puis, on trace les vecteurs $\vec{u}\ $ et $\ \vec{v}.$
Démontrons que $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires au vecteur $\vec{w}.$
En effet, d'après les résultats de la question $1\;)$, on a :
$$\vec{u}=\dfrac{1}{2}\vec{w}\quad\text{et}\quad\vec{v}=\dfrac{3}{2}\vec{w}$$
Par conséquent, $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires au vecteur $\vec{w}.$
Soit $A\ $ et $\ B$ deux points distincts du plan, $I$ milieu de $[AB]$
1) Démontrons que pour tout point $M$ du plan :
$$\overrightarrow{AM}+\overrightarrow{BM}=2\overrightarrow{IM}$$
En effet, par la relation de Chasles, en introduisant le point $I$ dans les vecteurs $\overrightarrow{AM}\ $ et $\ \overrightarrow{BM}$, on obtient :
$\begin{array}{rcl}\overrightarrow{AM}+\overrightarrow{BM}&=&\overrightarrow{AI}+\overrightarrow{IM}+\overrightarrow{BI}+\overrightarrow{IM}\\\\&=&2\overrightarrow{IM}+\underbrace{\overrightarrow{AI}+\overrightarrow{BI}}_{=\vec{0}}\end{array}$
Or, on sait que $I$ est le milieu de $[AB].$
Donc, $\overrightarrow{AI}+\overrightarrow{BI}=\vec{0}$
D'où, $\boxed{\overrightarrow{AM}+\overrightarrow{BM}=2\overrightarrow{IM}}$
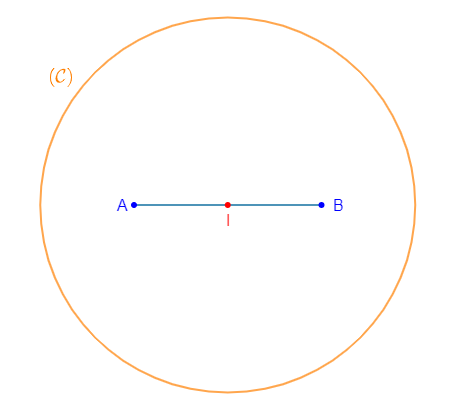
2) Déterminons et construisons l'ensemble $(\mathcal{C})$ des points $M$ du plan tels que :
$$||\overrightarrow{AM}+\overrightarrow{BM}||=2AB$$
En effet, d'après le résultat de la question $1\;)$, on a :
$$\overrightarrow{AM}+\overrightarrow{BM}=2\overrightarrow{IM}$$
Donc, en remplaçant $\overrightarrow{AM}+\overrightarrow{BM}$ par $2\overrightarrow{IM}$, on obtient :
$\begin{array}{rcl}||\overrightarrow{AM}+\overrightarrow{BM}||=2AB&\Leftrightarrow&||2\overrightarrow{IM}||=2AB\\\\&\Leftrightarrow&2||\overrightarrow{IM}||=2AB\\\\&\Leftrightarrow&||\overrightarrow{IM}||=\dfrac{2AB}{2}\\\\&\Leftrightarrow&||\overrightarrow{IM}||=AB\end{array}$
D'où, $\boxed{||\overrightarrow{IM}||=AB}$
Alors, $(\mathcal{C})$ est l'ensemble des points $M$ du plan équidistants à un même point $I$ et à une distance égale à la longueur $AB.$
C'est donc le cercle de centre $I$ et de rayon $AB.$
Soit un triangle $DIM$ et soit $A$ le milieu de $[DM].$
a) Construisons les points $T\ $ et $\ H$ tels que :
$$\overrightarrow{DT}=4\overrightarrow{DI}\quad\text{ et }\quad\overrightarrow{IH}=3\overrightarrow{IM}$$
b) Démontrons que $(TH)//(IA)$
En effet, pour démontrer que les droites $(TH)\ $ et $\ (IA)$ sont parallèles il suffit de montrer que les vecteurs $\overrightarrow{TH}\ $ et $\ \overrightarrow{IA}$ sont colinéaires.
On a : $\overrightarrow{IH}=3\overrightarrow{IM}$
Donc, par la relation de Chasles, introduisons le point $T$ dans le vecteur $\overrightarrow{IH}.$
On obtient :
$$\overrightarrow{IT}+\overrightarrow{TH}=3\overrightarrow{IM}$$
Utilisons encore la relation de Chasles pour introduire le point $D$ dans le vecteur $\overrightarrow{IT}.$
Ce qui donne :
$$\overrightarrow{ID}+\overrightarrow{DT}+\overrightarrow{TH}=3\overrightarrow{IM}$$
Or, on sait que : $\overrightarrow{DT}=4\overrightarrow{DI}$
Donc, en remplaçant $\overrightarrow{DT}$ par $4\overrightarrow{DI}$, on trouve :
$\begin{array}{rcl}\overrightarrow{ID}+\overrightarrow{DT}+\overrightarrow{TH}=3\overrightarrow{IM}&\Leftrightarrow&\overrightarrow{ID}+4\overrightarrow{DI}+\overrightarrow{TH}=3\overrightarrow{IM}\\\\&\Leftrightarrow&\overrightarrow{TH}=3\overrightarrow{IM}-\overrightarrow{ID}-4\overrightarrow{DI}\\\\&\Leftrightarrow&\overrightarrow{TH}=3\overrightarrow{IM}-\overrightarrow{ID}+4\overrightarrow{ID}\\\\&\Leftrightarrow&\overrightarrow{TH}=3\overrightarrow{IM}+3\overrightarrow{ID}\\\\&\Leftrightarrow&\overrightarrow{TH}=3\left(\overrightarrow{IM}+\overrightarrow{ID}\right)\end{array}$
Ainsi, en utilisant encore la relation de Chasles, introduisons le point $A$ dans les vecteurs $\overrightarrow{IM}\ $ et $\ \overrightarrow{ID}.$
On obtient :
$\begin{array}{rcl}\overrightarrow{TH}&=&3\left(\overrightarrow{IM}+\overrightarrow{ID}\right)\\\\&=&3\left(\overrightarrow{IA}+\overrightarrow{AM}+\overrightarrow{IA}+\overrightarrow{AD}\right)\\\\&=&3\left(2\overrightarrow{IA}+\underbrace{\overrightarrow{AM}+\overrightarrow{AD}}_{=\vec{0}}\right)\end{array}$
Par ailleurs, on sait que $A$ est le milieu de $[DM].$
Ce qui signifie que :
$$\overrightarrow{AM}+\overrightarrow{AD}=\vec{0}$$
D'où, $\boxed{\overrightarrow{TH}=6\overrightarrow{IA}}$
Ce qui montre que les vecteurs $\overrightarrow{TH}\ $ et $\ \overrightarrow{IA}$ sont colinéaires.
Par conséquent, les droites $(TH)\ $ et $\ (IA)$ sont parallèles.
Soit $ABC$ un triangle quelconque.
1) a) Montrons que l'égalité $\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}$ équivaut à l'égalité $\overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}.$
En effet, soit l'égalité :
$$\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}$$
Alors, par la relation de Chasles, introduisons le point $A$ dans les vecteurs $\overrightarrow{DB}\ $ et $\ \overrightarrow{DC}.$
On obtient :
$\begin{array}{rcl}\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}&\Leftrightarrow&\overrightarrow{DA}-3\left(\overrightarrow{DA}+\overrightarrow{AB}\right)+\left(\overrightarrow{DA}+\overrightarrow{AC}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{DA}-3\overrightarrow{DA}-3\overrightarrow{AB}+\overrightarrow{DA}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&-\overrightarrow{DA}-3\overrightarrow{AB}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AD}-3\overrightarrow{AB}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}\end{array}$
D'où, $\boxed{\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}\quad \Leftrightarrow\quad \overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}}$
Construisons le point $D.$
Pour construire le point $D$, on utilise la relation :
$$\overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}$$
b) Montrons que $\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}=-\overrightarrow{MD}$ quelque soit le point $M.$
En effet, par la relation de Chasles, en introduisant le point $D$ dans les vecteurs $\overrightarrow{MA}\;,\ \overrightarrow{MB}\ $ et $\ \overrightarrow{MC}$, on obtient :
$\begin{array}{rcl}\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}&=&\left(\overrightarrow{MD}+\overrightarrow{DA}\right)-3\left(\overrightarrow{MD}+\overrightarrow{DB}\right)+\left(\overrightarrow{MD}+\overrightarrow{DC}\right)\\\\&=&\overrightarrow{MD}+\overrightarrow{DA}-3\overrightarrow{MD}-3\overrightarrow{DB}+\overrightarrow{MD}+\overrightarrow{DC}\\\\&=&-\overrightarrow{MD}+\underbrace{\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}}_{=\vec{0}}\end{array}$
Or, d'après la question $1\;a\;)$, on a :
$$\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}$$
D'où, $\boxed{\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}=-\overrightarrow{MD}}$
c) Montrons que $\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{BD}$
D'après le résultat de la question $1\;b\;)$, on a :
$$\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}=-\overrightarrow{MD}$$
quelque soit le point $M.$
Donc, en posant $M=B$ ou en remplaçant $M$ par $B$ dans cette relation, on obtient :
$$\overrightarrow{BA}-3\overrightarrow{BB}+\overrightarrow{BC}=-\overrightarrow{BD}$$
D'où, $\boxed{\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{BD}}$
2) Soit $M$ un point quelconque, on pose :
$$\vec{V}=\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}$$
Montrons que :
$$\vec{V}=\overrightarrow{BA}+\overrightarrow{BC}$$
En effet, soit : $\vec{V}=\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}$
Alors, par la relation de Chasles, introduisons le point $B$ dans les vecteurs $ \overrightarrow{MA}\ $ et $\ \overrightarrow{MC}.$
On obtient :
$\begin{array}{rcl}\vec{V}&=&\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}\\\\&=&\left(\overrightarrow{MB}+\overrightarrow{BA}\right)-2\overrightarrow{MB}+\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\\\\&=&\overrightarrow{MB}+\overrightarrow{BA}-2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{BC}\\\\&=&\overrightarrow{BA}+\overrightarrow{BC}\end{array}$
Ainsi, $\boxed{\vec{V}=\overrightarrow{BA}+\overrightarrow{BC}}$
Plaçons le point $E$ défini par :
$$\vec{V}=\overrightarrow{AE}$$
Cela revient donc à placer le point $E$ tel que :
$$\overrightarrow{AE}=\overrightarrow{BA}+\overrightarrow{BC}$$
3) Montrons que les droites $(BD)\ $ et $\ (AE)$ sont parallèles.
Pour cela, il suffit de montrer que $\overrightarrow{AE}\ $ et $\ \overrightarrow{BD}$ sont colinéaires.
En effet, d'après le résultat de la question $1\;c\;)$, on a :
$$\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{BD}$$
Par ailleurs, d'après la question $2\;)$, on a :
$$\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AE}$$
Ainsi, $\boxed{\overrightarrow{AE}=-\overrightarrow{BD}}$
Ce qui signifie que les vecteurs $\overrightarrow{AE}\ $ et $\ \overrightarrow{BD}$ sont colinéaires.
Par conséquent, les droites $(BD)\ $ et $\ (AE)$ sont parallèles.
Soit $ABC$ un triangle
1) Construisons les points $M\ $ et $\ N$ tels que :
$$\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AB}\quad\text{ et }\quad\overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AC}$$
2) Démontrons que $(MN)//(BC)$
En effet, on a : $M\;,\ A\ $ et $\ B$ trois points alignés d'une part, $N\;,\ A\ $ et $\ C$ trois points alignés d'autre part, dans le même ordre.
Calculons alors les rapports :
$$\dfrac{\left\|\overrightarrow{AM}\right\|}{\left\|\overrightarrow{AB}\right\|}\quad\text{ et }\quad\dfrac{\left\|\overrightarrow{AN}\right\|}{\left\|\overrightarrow{AC}\right\|}$$
On a :
$\dfrac{\left\|\overrightarrow{AM}\right\|}{\left\|\overrightarrow{AB}\right\|}=\dfrac{\left\|-\dfrac{2}{3}\overrightarrow{AB}\right\|}{\left\|\overrightarrow{AB}\right\|}=\left|-\dfrac{2}{3}\right|\dfrac{\left\|\overrightarrow{AB}\right\|}{\left\|\overrightarrow{AB}\right\|}=\dfrac{2}{3}$
$\dfrac{\left\|\overrightarrow{AN}\right\|}{\left\|\overrightarrow{AC}\right\|}=\dfrac{\left\|-\dfrac{2}{3}\overrightarrow{AC}\right\|}{\left\|\overrightarrow{AC}\right\|}=\left|-\dfrac{2}{3}\right|\dfrac{\left\|\overrightarrow{AC}\right\|}{\left\|\overrightarrow{AC}\right\|}=\dfrac{2}{3}$
Ainsi,
$$\dfrac{\left\|\overrightarrow{AM}\right\|}{\left\|\overrightarrow{AB}\right\|}=\dfrac{\left\|\overrightarrow{AN}\right\|}{\left\|\overrightarrow{AC}\right\|}=\dfrac{2}{3}$$
Par conséquent, d'après la réciproque du théorème de Thalès, les droites $(MN)\ $ et $\ (BC)$ sont parallèles.
Autre méthode :
En effet, pour montrer que les droites $(MN)\ $ et $\ (BC)$ sont parallèles, il suffit de montrer que les vecteurs $\overrightarrow{MN}\ $ et $\ \overrightarrow{BC}$ sont colinéaires.
D'après la question $1\;)$, on a :
$\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AB}$
$\overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AC}$
Donc, en faisant la différence membre à membre de ces deux relations, on obtient :
$\begin{array}{rcl}\overrightarrow{AN}-\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AC}-\left(-\dfrac{2}{3}\overrightarrow{AB}\right)&\Leftrightarrow&\overrightarrow{AN}+\overrightarrow{MA}=-\dfrac{2}{3}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{AN}+\overrightarrow{MA}=-\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\\\\&\Leftrightarrow&\overrightarrow{AN}+\overrightarrow{MA}=-\dfrac{2}{3}\left(\overrightarrow{AC}+\overrightarrow{BA}\right)\\\\&\Leftrightarrow&\overrightarrow{MA}+\overrightarrow{AN}=-\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\end{array}$
En appliquant la relation de Chasles, on trouve :
$$\boxed{\overrightarrow{MN}=-\dfrac{2}{3}\overrightarrow{BC}}$$
Ce qui montre que les vecteurs $\overrightarrow{MN}\ $ et $\ \overrightarrow{BC}$ sont colinéaires.
Par conséquent, les droites $(MN)\ $ et $\ (BC)$ sont parallèles.
3) Soient $S\ $ et $\ T$ les milieux respectifs de $[BC]\ $ et $\ [MN].$
Démontrons que les points $A\;,\ S\ $ et $\ T$ sont alignés.
Soit :
$\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AB}$
$\overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AC}$
Alors, en additionnant membre à membre ces deux relations, on obtient :
$$\overrightarrow{AN}+\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AC}-\dfrac{2}{3}\overrightarrow{AB}$$
Ensuite, par la relation de Chasles, introduisons le point $T$ dans les vecteurs $\overrightarrow{AN}\ $ et $\ \overrightarrow{AM}$ puis, le point $S$ dans les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{AB}.$
On obtient :
$\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AC}-\dfrac{2}{3}\overrightarrow{AB}&\Leftrightarrow&\left(\overrightarrow{AT}+\overrightarrow{TN}\right)+\left(\overrightarrow{AT}+\overrightarrow{TM}\right)=-\dfrac{2}{3}\left(\overrightarrow{AS}+\overrightarrow{SC}\right)-\dfrac{2}{3}\left(\overrightarrow{AS}+\overrightarrow{SB}\right)\\\\&\Leftrightarrow&\overrightarrow{AT}+\overrightarrow{TN}+\overrightarrow{AT}+\overrightarrow{TM}=-\dfrac{2}{3}\overrightarrow{AS}-\dfrac{2}{3}\overrightarrow{SC}-\dfrac{2}{3}\overrightarrow{AS}-\dfrac{2}{3}\overrightarrow{SB}\\\\&\Leftrightarrow&2\overrightarrow{AT}+\underbrace{\overrightarrow{TN}+\overrightarrow{TM}}_{=\vec{0}}=-\dfrac{4}{3}\overrightarrow{AS}-\dfrac{2}{3}\left(\underbrace{\overrightarrow{SC}+\overrightarrow{SB}}_{=\vec{0}}\right)\end{array}$
Or, $T$ est milieu de $[MN]\ $ et $\ S$ milieu de $[BC].$
Donc, cela signifie :
$$\overrightarrow{TN}+\overrightarrow{TM}=\vec{0}\quad\text{ et }\quad\overrightarrow{SC}+\overrightarrow{SB}=\vec{0}$$
Ainsi,
$$2\overrightarrow{AT}=-\dfrac{4}{3}\overrightarrow{AS}$$
D'où, $\boxed{\overrightarrow{AT}=-\dfrac{2}{3}\overrightarrow{AS}}$
Par conséquent, les points $A\;,\ S\ $ et $\ T$ sont alignés.
Soit $ABC$ un triangle de centre de gravité $G\ $ et $\ I$ milieu de $[BC].$
1) Démontrons que pour tout point $M$ du plan :
$$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$$
$$2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}$$
Soit la relation : $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$
Alors, par la relation de Chasles, introduisons le point $G$ dans les vecteurs $\overrightarrow{MA}\;,\ \overrightarrow{MB}\ $ et $\ \overrightarrow{MC}.$
On obtient :
$\begin{array}{rcl}\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}&=&\left(\overrightarrow{MG}+\overrightarrow{GA}\right)+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)\\\\&=&\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\\\\&=&3\overrightarrow{MG}+\underbrace{\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}}_{=\vec{0}}\end{array}$
Or, $G$ est le centre de gravité du triangle $ABC.$
Ce qui entraine alors :
$$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$$
D'où, $\boxed{\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}}$
Soit la relation : $2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$
Alors, par la relation de Chasles, introduisons le point $I$ dans les vecteurs $\overrightarrow{MA}\;,\ \overrightarrow{MB}\ $ et $\ \overrightarrow{MC}.$
On obtient :
$\begin{array}{rcl}2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}&=&2\left(\overrightarrow{MI}+\overrightarrow{IA}\right)-\left(\overrightarrow{MI}+\overrightarrow{IB}\right)-\left(\overrightarrow{MI}+\overrightarrow{IC}\right)\\\\&=&2\overrightarrow{MI}+2\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB}-\overrightarrow{MI}-\overrightarrow{IC}\\\\&=&2\overrightarrow{IA}-\overrightarrow{IB}-\overrightarrow{IC}\\\\&=&2\overrightarrow{IA}-\left(\underbrace{\overrightarrow{IB}+\overrightarrow{IC}}_{=\vec{0}}\right)\end{array}$
Comme $I$ est le milieu de $[BC]$ alors,
$$\overrightarrow{IB}+\overrightarrow{IC}=\vec{0}$$
Par conséquent, $\boxed{2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}}$
2) Déterminons l'ensemble des points $M$ tels que les vecteurs $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\ $ et $\ 2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$ soient colinéaires.
En effet, d'après les résultats de la question $1\;)$, on a :
$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$
$2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}$
Donc, $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\ $ et $\ 2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$ colinéaires si, et seulement si, les vecteurs $3\overrightarrow{MG}\ $ et $\ 2\overrightarrow{IA}$ sont colinéaires.
Or, $3\overrightarrow{MG}\ $ et $\ 2\overrightarrow{IA}$ sont colinéaires si, et seulement si, les droites $(MG)\ $ et $\ (IA)$ sont parallèles.
$M$ appartient donc à la droite passant par $G$ et parallèle à $(IA).$
Mais on sait que la droite $(IA)$ ; médiane issue de $A$, passe aussi par le centre de gravité $G$ de ce triangle.
D'où, l'ensemble des points $M$ tels que les vecteurs $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\ $ et $\ 2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$ soient colinéaires est la droite $(IA).$
3) Déterminons l'ensemble des points $M$ tels que :
$$\left\|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right\|$$
En effet, d'après les résultats de la question $1\;)$, on a :
$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$
$2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}$
Donc, en remplaçant, on obtient :
$\begin{array}{rcl}\left\|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right\|&\Leftrightarrow&\left\|3\overrightarrow{MG}\right\|=\left\|2\overrightarrow{IA}\right\|\\\\&\Leftrightarrow&3\left\|\overrightarrow{MG}\right\|=2\left\|\overrightarrow{IA}\right\|\\\\&\Leftrightarrow&\left\|\overrightarrow{MG}\right\|=\dfrac{2}{3}\left\|\overrightarrow{IA}\right\|\end{array}$
D'où, l'ensemble des points $M$ tels que $\left\|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right\|$ est le cercle de centre $G$ et de rayon $\dfrac{2}{3}IA.$
Remarque :
$G$ centre de gravité alors, $AG=\dfrac{2}{3}IA.$
Donc, $A$ appartient au cercle de centre $G$ et de rayon $\dfrac{2}{3}IA.$
Par conséquent, l'ensemble des points $M$ vérifiant $\left\|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right\|$ est le cercle de centre $G$ et passant par $A.$
$ABCD$ est un parallélogramme, $I$ milieu de $[AB]\ $ et $\ J$ celui de $[CD]$
1) Démontrons que les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
Pour cela, il suffit juste de montrer que les vecteurs $\overrightarrow{ID}\ $ et $\ \overrightarrow{BJ}$ sont colinéaires.
En utilisant la relation de Chasles, on a :
$$\overrightarrow{ID}=\overrightarrow{IB}+\overrightarrow{BJ}+\overrightarrow{JD}\quad(*)$$
Comme $I$ milieu de $[AB]\ $ et $\ J$ milieu de $[CD]$ alors :
$\overrightarrow{IB}=\dfrac{1}{2}\overrightarrow{AB}\ $ et $\ \overrightarrow{JD}=-\dfrac{1}{2}\overrightarrow{DC}$
Or, $\overrightarrow{AB}=\overrightarrow{DC}$ car $ABCD$ est un parallélogramme donc, $\overrightarrow{IB}=-\overrightarrow{JD}$
Par suite, en reportant dans l'égalité $(*)$, on obtient :
$\begin{array}{rcl}\overrightarrow{ID}&=&\overrightarrow{IB}+\overrightarrow{BJ}+\overrightarrow{JD}\\\\&=&-\overrightarrow{JD}+\overrightarrow{BJ}+\overrightarrow{JD}\\\\&=&\overrightarrow{BJ}\end{array}$
Ainsi, $\overrightarrow{ID}=\overrightarrow{BJ}$
Ce qui signifie que $\overrightarrow{ID}\ $ et $\ \overrightarrow{BJ}$ sont colinéaires.
Par conséquent, les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
Autre méthode :
On a : $\overrightarrow{IB}=\overrightarrow{DJ}$ alors, $IBJD$ est un parallélogramme.
Par suite, $\overrightarrow{ID}=\overrightarrow{BJ}$
D'où, les droites $(ID)\ $ et $\ (JB)$ sont parallèles.
2) a) Construisons les points $M\ $ et $\ N$ tels que $\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AC}\ $ et $\ \overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}$
b) Démontrons que les points $M\ $ et $\ N$ appartiennent respectivement aux droites $(ID)\ $ et $\ (JB)$
Pour cela, il suffit de prouver que $D\;,\ M\;,\ I$ sont alignés de même que $B\;,\ N\;,\ J$
Ce qui revient donc à montrer que $\overrightarrow{IM}=k\overrightarrow{ID}\ $ et $\ \overrightarrow{JN}=k'\overrightarrow{JB}$ avec $k\ $ et $\ k'$ deux nombres réels.
On a :
$\begin{array}{rcl}\overrightarrow{IM}&=&\overrightarrow{IA}+\overrightarrow{AM}\quad\text{or, }\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AC}\\\\&=&\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{AC}\\\\&=&\overrightarrow{IA}+\dfrac{1}{3}\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\\\\&=&\dfrac{1}{3}\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\overrightarrow{IA}+\dfrac{1}{3}\overrightarrow{DC}\\\\&=&\dfrac{1}{3}\left(\overrightarrow{IA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\left(2\overrightarrow{IA}+\overrightarrow{DC}\right)\quad\text{or, }2\overrightarrow{IA}=\overrightarrow{BA}\\\\&=&\dfrac{1}{3}\overrightarrow{ID}+\dfrac{1}{3}\underbrace{\left(\overrightarrow{BA}+\overrightarrow{DC}\right)}_{=\vec{0}}\\\\&=&\dfrac{1}{3}\overrightarrow{ID}\end{array}$
Donc, $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}$
Ainsi, les points $D\;,\ M\;,\ I$ sont alignés et par conséquent, $M$ appartient à la droite $(ID).$
De la même manière, on a :
$\begin{array}{rcl}\overrightarrow{JN}&=&\overrightarrow{JC}+\overrightarrow{CN}\quad\text{or, }\overrightarrow{CN}=\dfrac{1}{3}\overrightarrow{CA}\\\\&=&\overrightarrow{JC}+\dfrac{1}{3}\overrightarrow{CA}\\\\&=&\overrightarrow{JC}+\dfrac{1}{3}\left(\overrightarrow{CB}+\overrightarrow{BA}\right)\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{2}{3}\overrightarrow{JC}+\dfrac{1}{3}\overrightarrow{BA}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{1}{3}\left(2\overrightarrow{JC}+\overrightarrow{BA}\right)\quad\text{or, }2\overrightarrow{JC}=\overrightarrow{DC}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}+\dfrac{1}{3}\underbrace{\left(\overrightarrow{BA}+\overrightarrow{DC}\right)}_{=\vec{0}}\\\\&=&\dfrac{1}{3}\overrightarrow{JB}\end{array}$
Donc, $\overrightarrow{JN}=\dfrac{1}{3}\overrightarrow{JB}$
Par suite, les points $J\;,\ N\;,\ B$ sont alignés.
D'où, $N$ appartient à la droite $(JB).$
3) Démontrons que $MINJ$ est un parallélogramme
Soit : $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}\ $ et $\ \overrightarrow{JN}=\dfrac{1}{3}\overrightarrow{JB}$
Or, d'après la question 1), on a : $\overrightarrow{ID}=\overrightarrow{BJ}$
Donc, $\overrightarrow{IM}=\dfrac{1}{3}\overrightarrow{ID}=\dfrac{1}{3}\overrightarrow{BJ}=-\overrightarrow{JN}$
Par suite, $\overrightarrow{IM}=\overrightarrow{NJ}$
D'où, $MINJ$ est un parallélogramme.
4) Soit $\{E\}=(ID)\cap(BC)$, montrons que $B$ est milieu de $[CE]$
En effet, dans le triangle $CDE$, la droite $(JB)$ parallèle à $(DE)$ et passant par $J$, milieu de $[CD]$, coupe $[CE]$ au point $B.$
Ainsi, d'après le théorème de la droite des milieux, $B$ est milieu de $[CE].$
$ABCD$ est un parallélogramme, $E\ $ et $\ F$ deux points définis par :
$$\overrightarrow{AE}=-\dfrac{1}{2}\overrightarrow{AD}\quad\text{ et }\quad\overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{BA}$$
1) Exprimons $\overrightarrow{AC}\ $ et $\ \overrightarrow{AF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}.$
En effet, par la relation de Chasles, introduisons le point $B$ dans le vecteur $\overrightarrow{AC}.$
On obtient alors :
$$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$$
Or, $ABCD$ est un parallélogramme, donc :
$$\overrightarrow{BC}=\overrightarrow{AD}$$
Ainsi, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{AD}$, on trouve :
$\boxed{\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}}$
Soit : $\overrightarrow{AE}=-\dfrac{1}{2}\overrightarrow{AD}\ $ et $\ \overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{BA}.$
Alors, en additionnant membre à membre ces deux égalités, on obtient :
$$\underbrace{\overrightarrow{AE}+\overrightarrow{EF}}_{=\overrightarrow{AF}}=-\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{BA}$$
En appliquant la relation de Chasles, on trouve :
$\begin{array}{rcl}\overrightarrow{AF}&=&-\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{BA}\\\\&=&-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\end{array}$
D'où, $\boxed{\overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}}$
2) Démontrons que les points $A\;,\ F\ $ et $\ C$ sont alignés.
En effet, les points $A\;,\ F\ $ et $\ C$ sont alignés si, et seulement si, les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{AF}$ sont colinéaires.
Soit : $\overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}$
Alors, en mettant $-\dfrac{1}{2}$ en facteur, on obtient :
$\begin{array}{rcl}\overrightarrow{AF}&=&-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\\\\&=&-\dfrac{1}{2}\left(\underbrace{\overrightarrow{AB}+\overrightarrow{AD}}_{=\overrightarrow{AC}}\right)\\\\&=&-\dfrac{1}{2}\overrightarrow{AC}\end{array}$
D'où, $\boxed{\overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AC}}$
Ce qui signifie que les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{AF}$ sont colinéaires.
Par conséquent, les points $A\;,\ F\ $ et $\ C$ sont alignés.
3) Exprimons les coordonnées de $A\;,\ F\ $ et $\ C$ dans le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AD}).$
En effet, dans le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AD})$, on a : $A$ origine du repère et $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$ constituent les vecteurs de base de ce repère.
Ainsi,
$$A\begin{pmatrix}0\\\\0\end{pmatrix}$$
Par ailleurs, d'après les résultats de la question $1\;)$, on a :
$$\overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}$$
Donc,
$$F\begin{pmatrix}-\dfrac{1}{2}\\\\-\dfrac{1}{2}\end{pmatrix}$$
De même, on a :
$$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$$
D'où,
$$C\begin{pmatrix}1\\\\1\end{pmatrix}$$
Calculons les coordonnées de $\overrightarrow{AF}\ $ et $\ \overrightarrow{AC}$
Soit : $\overrightarrow{AF}\begin{pmatrix}x_{F}-x_{A}\\\\y_{F}-y_{A}\end{pmatrix}\ $ et $\ \overrightarrow{AC}\begin{pmatrix}x_{C}-x_{A}\\\\y_{C}-y_{A}\end{pmatrix}$
En remplaçant ces coordonnées par leur valeur, on trouve :
$$\overrightarrow{AF}\begin{pmatrix}-\dfrac{1}{2}\\\\-\dfrac{1}{2}\end{pmatrix}\quad\text{ et }\quad\overrightarrow{AC}\begin{pmatrix}1\\\\1\end{pmatrix}$$
Soit $ABCD$ un parallélogramme. On considère $E$ défini par $\overrightarrow{CE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$ et le point $F$ symétrique de $D$ par rapport à $E.$
1) Démontrons que $E$ est le milieu de $[AB]\ $ et $\ B$ le milieu de $[CF].$
Soit : $\overrightarrow{CE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$
Alors, par la relation de Chasles, en introduisant le point $B$ dans le vecteur $\overrightarrow{CE}$, on obtient :
$$\overrightarrow{CB}+\overrightarrow{BE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$$
Or, $ABCD$ est un parallélogramme, donc :
$$\overrightarrow{CB}=\overrightarrow{DA}$$
Par suite, en remplaçant $\overrightarrow{CB}$ par $\overrightarrow{DA}$, on trouve :
$$\overrightarrow{DA}+\overrightarrow{BE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$$
Ainsi, en appliquant les propriétés du calcul vectoriel, on obtient :
$\begin{array}{rcl}\overrightarrow{DA}+\overrightarrow{BE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}&\Leftrightarrow&\overrightarrow{BE}=-\overrightarrow{DA}+\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{BE}=-\dfrac{1}{2}\overrightarrow{AB}\\\\&=&\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BA}\end{array}$
D'où, $\boxed{\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BA}}$
Ce qui démontre que $E$ est le milieu de $[AB].$
Pour montrer que $B$ est milieu de $[CF]$, il suffit de montrer que :
$$\overrightarrow{BC}+\overrightarrow{BF}=\vec{0}$$
Soit la somme vectorielle : $\overrightarrow{BC}+\overrightarrow{BF}$
Alors, par la relation de Chasles, introduisons le point $E$ dans le vecteur $\overrightarrow{BF}.$
On obtient :
$$\overrightarrow{BC}+\overrightarrow{BF}=\overrightarrow{BC}+\overrightarrow{BE}+\overrightarrow{EF}$$
Or, on sait que $ABCD$ est un parallélogramme, donc :
$$\overrightarrow{BC}=\overrightarrow{AD}$$
Par ailleurs, $F$ étant le symétrique de $D$ par rapport à $E$ alors,
$$\overrightarrow{EF}=\overrightarrow{DE}$$
Ainsi, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{AD}\ $ et $\ \overrightarrow{EF}$ par $\overrightarrow{DE}$, on obtient :
$$\overrightarrow{BC}+\overrightarrow{BF}=\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{DE}$$
D'après Chasles, on trouve :
$$\overrightarrow{BC}+\overrightarrow{BF}=\overrightarrow{AE}+\overrightarrow{BE}$$
Comme $E$ est milieu de $[AB]$ alors, $\overrightarrow{AE}+\overrightarrow{BE}=\vec{0}.$
D'où, $\boxed{\overrightarrow{BC}+\overrightarrow{BF}=\vec{0}}$
Ce qui démontre que $B$ est le milieu de $[CF].$
2) Démontrons que $ADBF$ est un parallélogramme
D'après les résultats de la question $1\;)$, on a : $E$ milieu de $[AB].$
Ce qui se traduit par :
$$\overrightarrow{AE}+\overrightarrow{BE}=\vec{0}$$
Par ailleurs, on sait que $F$ est le symétrique de $D$ par rapport à $E.$
Ce qui signifie que $E$ est le milieu de $[DF].$
Ce qui peut encore s'écrire :
$$\overrightarrow{DE}+\overrightarrow{FE}=\vec{0}$$
Alors, en additionnant membre à membre ces deux égalités, on trouve :
$$\overrightarrow{AE}+\overrightarrow{BE}+\overrightarrow{DE}+\overrightarrow{FE}=\vec{0}$$
Ce qui montre que $ADBF$ est un parallélogramme de centre $E.$
Autre méthode :
On a : dans le triangle $CDF$, la droite $(AB)$ passant par $E$ milieu de $[DF]$ coupe $[CF]$ au point $B.$
Donc, d'après la réciproque du théorème de la droite des milieux, $B$ est milieu de $[CF].$
On considère l'hexagone régulier $ABCDEF$ de centre $O$ ci-dessus, et $I\ $ et $\ J$ les milieux respectifs des segments $[AB]\ $ et $\ [ED].$ En utilisant les lettres de la figure citons :
a) deux vecteurs égaux
En effet, deux vecteurs sont égaux si, et seulement si, ils ont même direction, même sens et même norme ou longueur.
Ainsi, $\overrightarrow{AF}\ $ et $\ \overrightarrow{OE}$ sont deux vecteurs égaux.
b) deux vecteurs colinéaires de sens contraire et de normes distinctes.
$\overrightarrow{AD}\ $ et $\ \overrightarrow{CB}$ sont deux vecteurs colinéaires de sens contraire et de normes distinctes.
c) deux vecteurs colinéaires de même sens et de normes différentes.
$\overrightarrow{AB}\ $ et $\ \overrightarrow{JD}$ sont deux vecteurs colinéaires de même sens et de normes différentes.
d) deux vecteurs orthogonaux.
$\overrightarrow{IJ}\ $ et $\ \overrightarrow{FC}$ sont deux vecteurs orthogonaux.
e) deux vecteurs non colinéaires et de même norme.
$\overrightarrow{EF}\ $ et $\ \overrightarrow{DC}$ sont deux vecteurs non colinéaires et de même norme.
f) deux vecteurs opposés.
En effet, deux vecteurs sont opposés si, et seulement si, ils ont même direction, même norme mais de sens contraire.
Ainsi, $\overrightarrow{IA}\ $ et $\ \overrightarrow{IB}$ sont deux vecteurs opposés.
g) deux vecteurs non colinéaires et de normes distinctes.
$\overrightarrow{AD}\ $ et $\ \overrightarrow{OB}$ sont deux vecteurs non colinéaires et de normes distinctes.
On considère la figure ci-dessous :
1) Citons tous les vecteurs égaux à $\overrightarrow{AB}.$
Les vecteurs égaux à $\overrightarrow{AB}$ sont : $\overrightarrow{HE}\ $ et $\ \overrightarrow{GF}$
Ainsi, on a : $\boxed{\overrightarrow{AB}=\overrightarrow{HE}=\overrightarrow{GF}}$
2) Citons tous les vecteurs égaux à $\overrightarrow{FE}.$
Les vecteurs égaux à $\overrightarrow{FE}$ sont : $\overrightarrow{ED}\;,\ \overrightarrow{GH}\ $ et $\ \overrightarrow{BC}$
Donc, on a : $\boxed{\overrightarrow{FE}=\overrightarrow{ED}=\overrightarrow{GH}=\overrightarrow{BC}}$
3) Déterminons un ou plusieurs vecteurs égaux à $\overrightarrow{AB}+\overrightarrow{FE}.$
En effet, comme :
$\overrightarrow{AB}=\overrightarrow{HE}=\overrightarrow{GF}$
$\overrightarrow{FE}=\overrightarrow{ED}=\overrightarrow{GH}=\overrightarrow{BC}$
Alors, en remplaçant puis, en appliquant la relation de Chasles, on obtient :
$\overrightarrow{AB}+\overrightarrow{FE}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
$\overrightarrow{AB}+\overrightarrow{FE}=\overrightarrow{HE}+\overrightarrow{ED}=\overrightarrow{HD}$
$\overrightarrow{AB}+\overrightarrow{FE}=\overrightarrow{GF}+\overrightarrow{FE}=\overrightarrow{GE}$
Par conséquent, les vecteurs égaux à $\overrightarrow{AB}+\overrightarrow{FE}$ sont : $\overrightarrow{AC}\;,\ \overrightarrow{HD}\ $ et $\ \overrightarrow{GE}$
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{FE}=\overrightarrow{AC}=\overrightarrow{HD}=\overrightarrow{GE}}$
4) Déterminons un vecteur égal aux vecteurs suivants :
a) $\overrightarrow{AB}+\overrightarrow{AH}$
En effet, on a : $\overrightarrow{AB}=\overrightarrow{HE}.$
Donc, en remplaçant $\overrightarrow{AB}$ par $\overrightarrow{HE}$ puis, en appliquant la relation de Chasles, on obtient :
$$\overrightarrow{AB}+\overrightarrow{AH}=\overrightarrow{HE}+\overrightarrow{AH}=\overrightarrow{AE}$$
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{AH}=\overrightarrow{AE}}$
b) $\overrightarrow{BA}+\overrightarrow{BC}$
En effet, on a : $\overrightarrow{BA}=\overrightarrow{FG}\ $ et $\ \overrightarrow{BC}=\overrightarrow{GH}$
Donc, en remplaçant $\overrightarrow{BA}$ par $\overrightarrow{FG}\ $ et $\ \overrightarrow{BC}$ par $\overrightarrow{GH}$ puis, en appliquant la relation de Chasles, on obtient :
$$\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{FG}+\overrightarrow{GH}=\overrightarrow{FH}$$
Ainsi, $\boxed{\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{FH}}$
c) $\overrightarrow{BC}+\overrightarrow{DE}$
En effet, comme $\overrightarrow{BC}=\overrightarrow{ED}$ alors, en remplaçant $\overrightarrow{BC}$ par $\overrightarrow{ED}$ puis, en utilisant la relation de Chasles, on obtient :
$$\overrightarrow{BC}+\overrightarrow{DE}=\overrightarrow{ED}+\overrightarrow{DE}=\vec{0}$$
D'où, $\boxed{\overrightarrow{BC}+\overrightarrow{DE}=\vec{0}}$
d) $\overrightarrow{BF}+\overrightarrow{GF}$
En effet, on sait que : $\overrightarrow{AB}=\overrightarrow{GF}.$
Par suite, $ABFG$ est un parallélogramme.
Par conséquent, $\overrightarrow{BF}=\overrightarrow{AG}.$
Donc, en remplaçant $\overrightarrow{BF}$ par $\overrightarrow{AG}$ puis, en utilisant la relation de Chasles, on trouve :
$$\overrightarrow{BF}+\overrightarrow{GF}=\overrightarrow{AG}+\overrightarrow{GF}=\overrightarrow{AF}$$
D'où, $\boxed{\overrightarrow{BF}+\overrightarrow{GF}=\overrightarrow{AF}}$
e) $\overrightarrow{AE}+\overrightarrow{FB}$
En effet, comme $\overrightarrow{BC}=\overrightarrow{FE}$ alors, $BCEF$ est un parallélogramme.
Par conséquent, $\overrightarrow{FB}=\overrightarrow{EC}.$
Ainsi, en remplaçant $\overrightarrow{FB}$ par $\overrightarrow{EC}$ puis, en appliquant la relation de Chasles, on trouve :
$$\overrightarrow{AE}+\overrightarrow{FB}=\overrightarrow{AE}+\overrightarrow{EC}=\overrightarrow{AC}$$
D'où, $\boxed{\overrightarrow{AE}+\overrightarrow{FB}=\overrightarrow{AC}}$
N.B. Pour chacune des réponses, on utilisera uniquement les lettres de la figure.
$A\;,\ B\;,\ C\;,\ D$ sont quatre points.
Démontrons que :
1) $\overrightarrow{AB}-\overrightarrow{CD}-(\overrightarrow{AB}-\overrightarrow{CA})=\overrightarrow{DA}$
En utilisant les propriétés du calcul vectoriel puis, en appliquant la relation de Chasles, on obtient :
$\begin{array}{rcl} \overrightarrow{AB}-\overrightarrow{CD}-(\overrightarrow{AB}-\overrightarrow{CA})&=&\overrightarrow{AB}+\overrightarrow{DC}-\overrightarrow{AB}+\overrightarrow{CA}\\\\&=&\overrightarrow{AB}+\overrightarrow{DC}+\overrightarrow{BA}+\overrightarrow{CA}\\\\&=&\underbrace{\overrightarrow{AB}+\overrightarrow{BA}}_{=\vec{0}}+\underbrace{\overrightarrow{DC}+\overrightarrow{CA}}_{=\overrightarrow{DA}}\\\\&=&\overrightarrow{DA}\end{array}$
D'où, $\boxed{\overrightarrow{AB}-\overrightarrow{CD}-(\overrightarrow{AB}-\overrightarrow{CA})=\overrightarrow{DA}}$
2) $\overrightarrow{AD}+\overrightarrow{BC}=(\overrightarrow{AC}+\overrightarrow{BD})$
Par la relation de Chasles, introduisons le point $D$ dans le vecteur $\overrightarrow{BC}$ puis, appliquons les propriétés du calcul vectoriel
On obtient alors :
$\begin{array}{rcl} \overrightarrow{AD}+\overrightarrow{BC}&=&\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{DC}\\\\&=&\underbrace{\overrightarrow{AD}+\overrightarrow{DC}}_{=\overrightarrow{AC}}+\overrightarrow{BD}\\\\&=&\overrightarrow{AC}+\overrightarrow{BD}\end{array}$
D'où, $\boxed{\overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{BD}}$
Écrivons les vecteurs suivants en utilisant le moins de vecteurs possibles :
Soit : $\vec{u}=\overrightarrow{DE}+\overrightarrow{AB}-\overrightarrow{DB}$ (1 vecteur)
En effet, en utilisant les propriétés du calcul vectoriel puis, en appliquant la relation de Chasles, on obtient :
$\begin{array}{rcl} \vec{u}&=&\overrightarrow{DE}+\overrightarrow{AB}-\overrightarrow{DB}\\\\&=&\overrightarrow{DE}+\underbrace{\overrightarrow{AB}+\overrightarrow{BD}}_{=\overrightarrow{AD}}\\\\&=&\overrightarrow{DE}+\overrightarrow{AD}\\\\&=&\underbrace{\overrightarrow{AD}+\overrightarrow{DE}}_{=\overrightarrow{AE}}\end{array}$
D'où, $\boxed{\vec{u}=\overrightarrow{AE}}$
Soit : $\vec{v}=2(\overrightarrow{AB}+\overrightarrow{AC})+\overrightarrow{BC}$ (2 vecteurs)
Alors, en appliquant la relation de Chasles puis, les propriétés du calcul vectoriel, on obtient :
$\begin{array}{rcl} \vec{v}&=&2\left(\overrightarrow{AB}+\overrightarrow{AC}\right)+\overrightarrow{BC}\\\\&=&2\overrightarrow{AB}+2\overrightarrow{AC}+\overrightarrow{BC}\\\\&=&\overrightarrow{AB}+\underbrace{\overrightarrow{AB}+\overrightarrow{BC}}_{=\overrightarrow{AC}}+2\overrightarrow{AC}\\\\&=&\overrightarrow{AB}+\overrightarrow{AC}+2\overrightarrow{AC}\\\\&=&\overrightarrow{AB}+3\overrightarrow{AC}\end{array}$
D'où, $\boxed{\vec{v}=\overrightarrow{AB}+3\overrightarrow{AC}}$
Soit : $\vec{w}=\dfrac{1}{2}\overrightarrow{BA}-2\left(\overrightarrow{DB}-\dfrac{1}{4}\overrightarrow{AC}\right)$ (2 vecteurs)
Alors, en appliquant les propriétés du calcul vectoriel puis, la relation de Chasles, on obtient :
$\begin{array}{rcl} \vec{w}&=&\dfrac{1}{2}\overrightarrow{BA}-2\left(\overrightarrow{DB}-\dfrac{1}{4}\overrightarrow{AC}\right)\\\\&=&\dfrac{1}{2}\overrightarrow{BA}-2\overrightarrow{DB}+\dfrac{1}{2}\overrightarrow{AC}\\\\&=&\dfrac{1}{2}\left(\underbrace{\overrightarrow{BA}+\overrightarrow{AC}}_{=\overrightarrow{BC}}\right)+2\overrightarrow{BD}\\\\&=&\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{BD}\end{array}$
D'où, $\boxed{\vec{w}=\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{BD}}$
$O\ $ et $\ A$ sont deux points distincts :
1) Plaçons les points $M\;,\ N\;,\ P$ tels que :
a) $\overrightarrow{OM}=2\overrightarrow{OA}$
b) $\overrightarrow{ON}=-3.5\overrightarrow{OA}=-\dfrac{7}{2}\overrightarrow{OA}$
c) $\overrightarrow{OP}=-7\overrightarrow{OA}$
2) a) Exprimons le vecteur $\overrightarrow{OM}+\overrightarrow{ON}$ en fonction de $\overrightarrow{OA}.$
En effet, d'après la question $1\;)$ on a :
$\overrightarrow{OM}=2\overrightarrow{OA}$
$\overrightarrow{ON}=-\dfrac{7}{2}\overrightarrow{OA}$
Donc, en remplaçant $\overrightarrow{OM}\ $ et $\ \overrightarrow{ON}$ par leur expression puis, en appliquant les propriétés du calcul vectoriel, on trouve :
$\begin{array}{rcl} \overrightarrow{OM}+\overrightarrow{ON}&=&2\overrightarrow{OA}-\dfrac{7}{2}\overrightarrow{OA}\\\\&=&\dfrac{4}{2}\overrightarrow{OA}-\dfrac{7}{2}\overrightarrow{OA}\\\\&=&-\dfrac{3}{2}\overrightarrow{OA}\end{array}$
D'où, $\boxed{\overrightarrow{OM}+\overrightarrow{ON}=-\dfrac{3}{2}\overrightarrow{OA}}$
b) Exprimons le vecteur $\overrightarrow{OP}$ en fonction de $\overrightarrow{ON}.$
On a : $\overrightarrow{OP}=-7\overrightarrow{OA}$
Or, on sait que :
$\begin{array}{rcl}\overrightarrow{ON}&=&-3.5\overrightarrow{OA}\\\\&=&\dfrac{-7}{2}\overrightarrow{OA}\\\\&=&\dfrac{-7\overrightarrow{OA}}{2}\quad\text{ Or, on sait que :}\ -7\overrightarrow{OA}=\overrightarrow{OP}\\\\&=&\dfrac{\overrightarrow{OP}}{2}\end{array}$
Ainsi,
$$\overrightarrow{ON}=\dfrac{\overrightarrow{OP}}{2}$$
D'où, $\boxed{\overrightarrow{OP}=2\overrightarrow{ON}}$
$A\;,\ B\;,\ C\ $ et $\ D$ sont quatre points quelconques du plan.
1) Construisons les points $R\ $ et $\ S$ tels que :
$$\overrightarrow{AR}=\overrightarrow{AB}+\overrightarrow{CD}\quad\text{ et }\quad\overrightarrow{AS}=\overrightarrow{AD}+\overrightarrow{CB}$$
Nous remarquons que $R=S$ ; autrement dit, les points $R\ $ et $\ S$ sont confondus.
2) Démontrons que :
$$\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$$
En effet, par la relation de Chasles, en introduisant le point $C$ dans le vecteur $\overrightarrow{AB}$ puis, en utilisant les propriétés du calcul vectoriel, on obtient :
$\begin{array}{rcl}\overrightarrow{AB}+\overrightarrow{CD}&=&\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{CD}\\\\&=&\underbrace{\overrightarrow{AC}+\overrightarrow{CD}}_{=\overrightarrow{AD}}+\overrightarrow{CB}\\\\&=&\overrightarrow{AD}+\overrightarrow{CB}\end{array}$
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}}$
Par ailleurs, d'après le résultat de la question $1\,)$, on a : les points $R\ $ et $\ S$ confondus.
Ce qui entraine,
$$\overrightarrow{AR}=\overrightarrow{AS}$$
Or, on sait que :
$$\overrightarrow{AR}=\overrightarrow{AB}+\overrightarrow{CD}\quad\text{ et }\quad\overrightarrow{AS}=\overrightarrow{AD}+\overrightarrow{CB}$$
Par conséquent, $\boxed{\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}}$
$ABCD$ est un parallélogramme de centre $O.$
1) Calculons la somme vectorielle :
$$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}$$
En effet, comme $ABCD$ est un parallélogramme de centre $O$ alors, $O$ est le milieu de $[AC]$ et de $[BD].$
Par suite :
$$\overrightarrow{OA}+\overrightarrow{OC}=\vec{0}\quad\text{et}\quad\overrightarrow{OB}+\overrightarrow{OD}=\vec{0}$$
Par conséquent,
$\begin{array}{rcl}\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}&=&\underbrace{\overrightarrow{OA}+\overrightarrow{OC}}_{=\vec{0}}+\underbrace{\overrightarrow{OB}+\overrightarrow{OD}}_{=\vec{0}}\\\\&=&\vec{0}\end{array}$
D'où, $\boxed{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\vec{0}}$
2) $M$ étant un point quelconque du plan, plaçons les points $E\;,\ F\;,\ G\ $ et $\ H$ tels que :
$$\overrightarrow{ME}=\overrightarrow{AB}\;;\ \overrightarrow{MF}=\overrightarrow{BC}\;;\ \overrightarrow{MG}=\overrightarrow{CD}\quad\text{et}\quad\overrightarrow{MH}=\overrightarrow{DA}$$
Démontrons que le quadrilatère $EFGH$ est un parallélogramme.
Pour cela, calculons la somme vectorielle :
$$\overrightarrow{ME}+\overrightarrow{MF}+\overrightarrow{MG}+\overrightarrow{MH}$$
On a :
$\begin{array}{rcl}\overrightarrow{ME}+\overrightarrow{MF}+\overrightarrow{MG}+\overrightarrow{MH}&=&\underbrace{\overrightarrow{AB}+\overrightarrow{BC}}_{=\overrightarrow{AC}}+\underbrace{\overrightarrow{CD}+\overrightarrow{DA}}_{=\overrightarrow{CA}}\\\\&=&\overrightarrow{AC}+\overrightarrow{CA}\\\\&=&\vec{0}\end{array}$
Ainsi, $\boxed{\overrightarrow{ME}+\overrightarrow{MF}+\overrightarrow{MG}+\overrightarrow{MH}=\vec{0}}$
Par conséquent, $EFGH$ est un parallélogramme de centre $M.$
$OAB$ est un triangle, $D\ $ et $\ C$ les points tels que :
$$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OB}\quad\text{ et }\quad\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0}$$
1) Démontrons que $O$ est le milieu de $[CD].$
En effet, $O$ est le milieu du segment $[CD]$ si, et seulement si :
$$\overrightarrow{OD}+\overrightarrow{OC}=\vec{0}$$
On a :
$$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0}$$
Or, on sait que :
$$\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OB}$$
Donc, en remplaçant $\overrightarrow{OA}+\overrightarrow{OB}$ par $\overrightarrow{OD}$, on obtient :
$$\overrightarrow{OD}+\overrightarrow{OC}=\vec{0}$$
Ce qui montre que $O$ est le milieu de $[CD].$
2) $E\ $ et $\ F$ sont les points tels que :
$$\overrightarrow{OE}=\overrightarrow{OA}+\overrightarrow{OC}\quad\text{ et }\quad\overrightarrow{OF}=\overrightarrow{OB}+\overrightarrow{OC}$$
Démontons que $ABFE$ est un parallélogramme
Pour cela, calculons la somme vectorielle :
$$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OF}+\overrightarrow{OE}$$
Alors, en remplaçant, $\overrightarrow{OE}\ $ et $\ \overrightarrow{OF}$ par leur expression, on obtient :
$\begin{array}{rcl}\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OF}+\overrightarrow{OE}&=&\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OA}+\overrightarrow{OC}\\\\&=&\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\\\\&=&2\left(\underbrace{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}_{=\vec{0}}\right)\\\\&=&\vec{0}\end{array}$
Ainsi, $\boxed{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OF}+\overrightarrow{OE}=\vec{0}}$
Par conséquent, $ABFE$ est un parallélogramme de centre $O.$
Autre méthode :
Pour montrer que $ABFE$ est un parallélogramme, il suffit de montrer que :
$$\overrightarrow{AB}=\overrightarrow{EF}$$
En effet, on a : $\overrightarrow{OF}=\overrightarrow{OB}+\overrightarrow{OC}$
Donc, par la relation de Chasles, introduisons le point $E$ dans le vecteur $\overrightarrow{OF}.$
On obtient alors :
$$\overrightarrow{OE}+\overrightarrow{EF}=\overrightarrow{OB}+\overrightarrow{OC}\ \Rightarrow\ \overrightarrow{EF}=\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OE}$$
Ainsi, en remplaçant $\overrightarrow{OE}$ par son expression puis, en utilisant la relation de Chasles et les propriétés du calcul vectoriel, on trouve :
$\begin{array}{rcl}\overrightarrow{EF}&=&\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OE}\\\\&=&\overrightarrow{OB}+\overrightarrow{OC}-\left(\overrightarrow{OA}+\overrightarrow{OC}\right)\\\\&=&\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OA}-\overrightarrow{OC}\\\\&=&\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{AO}+\overrightarrow{CO}\\\\&=&\underbrace{\overrightarrow{AO}+\overrightarrow{OB}}_{=\overrightarrow{AB}}+\underbrace{\overrightarrow{OC}+\overrightarrow{CO}}_{=\vec{0}}\\\\&=&\overrightarrow{AB}\end{array}$
D'où, $\boxed{\overrightarrow{EF}=\overrightarrow{AB}}$
Par conséquent, le quadrilatère $ABFE$ est un parallélogramme.
$A\;,\ B\;,\ C\;,\ D$ sont quatre points
1) Construisons les points $E\;,\ F$ tels que :
$$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}\quad\text{ et }\quad\overrightarrow{AF}=\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}$$
On a :
$\begin{array}{rcl}\overrightarrow{AE}&=&\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}\\\\&=&\overrightarrow{AB}+\underbrace{\overrightarrow{AC}+\overrightarrow{CB}}_{=\overrightarrow{AB}}\\\\&=&\overrightarrow{AB}+\overrightarrow{AB}\\\\&=&2\overrightarrow{AB}\end{array}$
Donc, $\boxed{\overrightarrow{AE}=2\overrightarrow{AB}}$
On peut ainsi utiliser cette nouvelle expression du vecteur $\overrightarrow{AE}$ pour construire le point $E.$
De la même manière, on a :
$\begin{array}{rcl}\overrightarrow{AF}&=&\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}\\\\&=&\overrightarrow{AB}+\underbrace{\overrightarrow{CA}+\overrightarrow{AD}}_{=\overrightarrow{CD}}\\\\&=&\overrightarrow{AB}+\overrightarrow{CD}\end{array}$
Ainsi, $\boxed{\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{CD}}$
Par conséquent, on peut utiliser cette nouvelle expression de $\overrightarrow{AF}$ pour construire le point $F.$
2) Montrons que :
$$\overrightarrow{FE}=\overrightarrow{AC}+\overrightarrow{DB}$$
En effet, on a : $\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}$
Alors, en introduisant le point $F$ dans le vecteur $\overrightarrow{AE}$, par la relation de Chasles, on obtient :
$$\overrightarrow{AF}+\overrightarrow{FE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}$$
Ce qui entraine :
$$\overrightarrow{FE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}-\overrightarrow{AF}$$
Or, on sait que : $\overrightarrow{AF}=\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}$
Donc, en remplaçant $\overrightarrow{AF}$ par $\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}$ puis, en utilisant les propriétés du calcul vectoriel et la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{FE}&=&\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}-\overrightarrow{AF}\\\\&=&\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}-\left(\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}\right)\\\\&=&\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}-\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AD}\\\\&=&\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{DA}\\\\&=&\underbrace{\overrightarrow{AB}+\overrightarrow{BA}}_{=\vec{0}}+\underbrace{\overrightarrow{DA}+\overrightarrow{AC}+\overrightarrow{CB}}_{=\overrightarrow{DB}}+\overrightarrow{AC}\\\\&=&\overrightarrow{DB}+\overrightarrow{AC}\end{array}$
D'où, $\boxed{\overrightarrow{FE}=\overrightarrow{AC}+\overrightarrow{DB}}$
Sur la figure, les quadrilatères $SALE\;,\ SAIC\;,\ SCAE\;,\ BAEL\;,\ LAIB\ $ et $\ BACI$ sont des parallélogrammes.
En n'utilisant que les points de la figure, écrire chacune des sommes suivantes sous forme d'un seul vecteur.
a) $\overrightarrow{AB}+\overrightarrow{AL}=\overrightarrow{CB}$
En effet, $SALE$ étant un parallélogramme alors,
$$\overrightarrow{AL}=\overrightarrow{SE}$$
Par ailleurs, comme $SCAE$ est un parallélogramme alors,
$$\overrightarrow{SE}=\overrightarrow{CA}$$
Par conséquent,
$$\overrightarrow{AL}=\overrightarrow{CA}$$
Ainsi, en remplaçant $\overrightarrow{AL}$ par $\overrightarrow{CA}$ puis, en utilisant la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{AB}+\overrightarrow{AL}&=&\overrightarrow{AB}+\overrightarrow{CA}\\\\&=&\overrightarrow{CA}+\overrightarrow{AB}\\\\&=&\overrightarrow{CB}\end{array}$
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{AL}=\overrightarrow{CB}}$
b) $\overrightarrow{AB}+\overrightarrow{BL}+\overrightarrow{LA}=\overrightarrow{AA}=\vec{0}$
En appliquant la relation de Chasles et les propriétés du calcul vectoriel, on obtient ce résultat.
c) $\overrightarrow{AB}-\overrightarrow{AL}=\overrightarrow{LB}$
En utilisant les propriétés du calcul vectoriel puis, la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{AB}-\overrightarrow{AL}&=&\overrightarrow{AB}+\overrightarrow{LA}\\\\&=&\overrightarrow{LA}+\overrightarrow{AB}\\\\&=&\overrightarrow{LB}\end{array}$
D'où, $\boxed{\overrightarrow{AB}-\overrightarrow{AL}=\overrightarrow{LB}}$
d) $\overrightarrow{AB}+\overrightarrow{AL}+\overrightarrow{AE}=\overrightarrow{CL}$
En effet, d'après le résultat de la question $a\;)$, on a :
$$\overrightarrow{AB}+\overrightarrow{AL}=\overrightarrow{CB}$$
Or, $BAEL$ est un parallélogramme. Donc,
$$\overrightarrow{AE}=\overrightarrow{BL}$$
Ainsi, en remplaçant $\overrightarrow{AE}$ par $\overrightarrow{BL}$ puis, en utilisant la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{AB}+\overrightarrow{AL}+\overrightarrow{AE}&=&\overrightarrow{CB}+\overrightarrow{BL}\\\\&=&\overrightarrow{CL}\end{array}$
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{AL}+\overrightarrow{AE}=\overrightarrow{CL}}$
e) $\overrightarrow{AE}-\left(\overrightarrow{CA}+\overrightarrow{SC}\right)=\overrightarrow{IS}$
En utilisant les propriétés du calcul vectoriel puis, la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{AE}-\left(\overrightarrow{CA}+\overrightarrow{SC}\right)&=&\overrightarrow{AE}-\left(\overrightarrow{SC}+\overrightarrow{CA}\right)\\\\&=&\overrightarrow{AE}-\overrightarrow{SA}\\\\&=&\overrightarrow{AE}+\overrightarrow{AS}\end{array}$
Or, on sait que : $SCAE$ est un parallélogramme.
Donc,
$$\overrightarrow{AE}=\overrightarrow{CS}$$
De même, $SAIC$ étant un parallélogramme alors,
$$\overrightarrow{CS}=\overrightarrow{IA}$$
Par conséquent,
$$\overrightarrow{AE}=\overrightarrow{IA}$$
Ainsi, en remplaçant $\overrightarrow{AE}$ par $\overrightarrow{IA}$ puis, en appliquant la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{AE}-\left(\overrightarrow{CA}+\overrightarrow{SC}\right)&=&\overrightarrow{AE}+\overrightarrow{AS}\\\\&=&\overrightarrow{IA}+\overrightarrow{AS}\\\\&=&\overrightarrow{IS}\end{array}$
D'où, $\boxed{\overrightarrow{AE}-\left(\overrightarrow{CA}+\overrightarrow{SC}\right)=\overrightarrow{IS}}$
f) $\overrightarrow{SA}-\overrightarrow{LB}=\overrightarrow{SE}$
En effet, comme $BAEL$ est un parallélogramme alors, on a :
$$\overrightarrow{LB}=\overrightarrow{EA}$$
Donc, en remplaçant $\overrightarrow{BL}$ par $\overrightarrow{AE}$ puis, en utilisant les propriétés du calcul vectoriel et la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{SA}-\overrightarrow{LB}&=&\overrightarrow{SA}-\overrightarrow{EA}\\\\&=&\overrightarrow{SA}+\overrightarrow{AE}\\\\&=&\overrightarrow{SE}\end{array}$
D'où, $\boxed{\overrightarrow{SA}-\overrightarrow{LB}=\overrightarrow{SE}}$
g) $\overrightarrow{SI}-\overrightarrow{EL}-\overrightarrow{SL}=\overrightarrow{LC}$
En effet, $SALE$ est un parallélogramme donc,
$$\overrightarrow{EL}=\overrightarrow{SA}$$
Par ailleurs, comme $SAIC$ est un parallélogramme alors,
$$\overrightarrow{SA}=\overrightarrow{CI}$$
Par conséquent,
$$\overrightarrow{EL}=\overrightarrow{CI}$$
Ainsi, en remplaçant $\overrightarrow{EL}$ par $\overrightarrow{CI}$ puis, en utilisant les propriétés du calcul vectoriel et la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{SI}-\overrightarrow{EL}-\overrightarrow{SL}&=&\overrightarrow{SI}-\overrightarrow{CI}-\overrightarrow{SL}\\\\&=&\overrightarrow{SI}+\overrightarrow{IC}+\overrightarrow{LS}\\\\&=&\overrightarrow{LS}+\overrightarrow{SI}+\overrightarrow{IC}\\\\&=&\overrightarrow{LC}\end{array}$
D'où, $\boxed{\overrightarrow{SI}-\overrightarrow{EL}-\overrightarrow{SL}=\overrightarrow{LC}}$
h) $\overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}=\overrightarrow{SB}$
En effet, en utilisant les propriétés du calcul vectoriel puis, la relation de Chasles, on a :
$\begin{array}{rcl}\overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}&=&\overrightarrow{SI}+\underbrace{\overrightarrow{SL}+\overrightarrow{LE}}_{=\overrightarrow{SE}}\\\\&=&\overrightarrow{SI}+\overrightarrow{SE}\end{array}$
Or, on sait que $SCAE$ est un parallélogramme.
Donc, on a :
$$\overrightarrow{SE}=\overrightarrow{CA}$$
Par ailleurs, $BACI$ étant un parallélogramme alors, on a :
$$\overrightarrow{CA}=\overrightarrow{IB}$$
Par conséquent :
$$\overrightarrow{SE}=\overrightarrow{IB}$$
Ainsi, en remplaçant $\overrightarrow{SE}$ par $\overrightarrow{IB}$ puis, en appliquant la relation de Chasles, on obtient :
$\begin{array}{rcl}\overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}&=&\overrightarrow{SI}+\overrightarrow{SE}\\\\&=&\underbrace{\overrightarrow{SI}+\overrightarrow{IB}}_{=\overrightarrow{SB}}\\\\&=&\overrightarrow{SB}\end{array}$
D'où, $\boxed{\overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}=\overrightarrow{SB}}$
Dans un triangle $ABC$, on considère par $M$ le milieu de $[AB]$, par $I$ celui de $[MC]\ $ et $\ K$ le point tel que $\overrightarrow{CK}=\dfrac{1}{3}\overrightarrow{CB}$
1) Montrons que :
$$\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\quad\text{et}\quad\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}$$
On a :
$\begin{array}{rcl}\overrightarrow{AI}&=&\overrightarrow{AC}+\overrightarrow{CI}\quad\text{or, }I\ \text{ milieu de }[CM]\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CM}\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\left(\overrightarrow{CA}+\overrightarrow{AM}\right)\\\\&=&\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AM}\quad\text{or, }M\ \text{ milieu de }[AB]\\\\&=&\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}\right)\\\\&=&\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{4}\overrightarrow{AB}\end{array}$
D'où, $\boxed{\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}}$
Soit :
$\begin{array}{rcl}\overrightarrow{AK}&=&\overrightarrow{AC}+\overrightarrow{CK}\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\left(\overrightarrow{CA}+\overrightarrow{AB}\right)\\\\&=&\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\\\\&=&\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{AB}\\\\&=&\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{AB}\end{array}$
Alors, $\boxed{\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}}$
2) En déduisons que les points $A\;,\ I\;,\ K$ sont alignés.
Pour cela, il suffit de montrer que $\overrightarrow{AI}=\alpha\overrightarrow{AK}$ avec $\alpha$ un nombre réel non nul.
D'après la question précédente, on peut constater que $4\overrightarrow{AI}=3\overrightarrow{AK}$
Ainsi, $\overrightarrow{AI}=\dfrac{3}{4}\overrightarrow{AK}$
D'où, les points $A\;,\ I\;,\ K$ sont alignés.
Autre méthode :
D'après le résultat de la question $1\;)$, on a :
$\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}$
$\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}$
Donc, dans le repère $\left(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$, les coordonnées des vecteurs $\overrightarrow{AI}\ $ et $\ \overrightarrow{AK}$ sont données par :
$$\overrightarrow{AI}\begin{pmatrix}\dfrac{1}{4}\\ \\\dfrac{1}{2}\end{pmatrix}\quad \text{et}\quad \overrightarrow{AK}\begin{pmatrix}\dfrac{1}{3}\\ \\\dfrac{2}{3}\end{pmatrix}$$
Calculons alors les rapports : $\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AK}}}}\ $ et $\ \dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AK}}}}$
Soit :
$\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AK}}}}=\dfrac{\dfrac{1}{4}}{\dfrac{1}{3}}=\dfrac{1}{4}\times\dfrac{3}{1}=\dfrac{3}{4}$
$\dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AK}}}}=\dfrac{\dfrac{1}{2}}{\dfrac{2}{3}}=\dfrac{1}{2}\times\dfrac{3}{2}=\dfrac{3}{4}$
On trouve alors une même valeur égale à $\dfrac{3}{4}.$
Ce qui signifie que les points $A\;,\ I\;,\ K$ sont alignés.
Explication :
En effet, on a :
$$\left\lbrace\begin{array}{lcl}\dfrac{x_{_{\overrightarrow{AI}}}}{x_{_{\overrightarrow{AK}}}}&=&\dfrac{3}{4}\\ \\\dfrac{y_{_{\overrightarrow{AI}}}}{y_{_{\overrightarrow{AK}}}}&=&\dfrac{3}{4}\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcl} x_{_{\overrightarrow{AI}}}&=&\dfrac{3}{4}\times x_{_{\overrightarrow{AK}}}\\ \\y_{_{\overrightarrow{AI}}}&=&\dfrac{3}{4}\times y_{_{\overrightarrow{AK}}}\end{array}\right.$$
Par conséquent, $\overrightarrow{AI}=\dfrac{3}{4}\overrightarrow{AK}$
Ce qui montre que les points $A\;,\ I\ $ et $\ K$ sont alignés.
Soit $k$ un réel et $M$ le point défini par $\overrightarrow{AM}=k\overrightarrow{AB}$
$M$ se projette en $K$ sur $(AC)$ parallèlement à $(BC)$ et en $N$ sur $(CD)$ parallèlement à $(BC)$
1) Montrons que $\overrightarrow{MK}=2k\overrightarrow{AD}\ $ et $\ \overrightarrow{NK}=(k-1)\overrightarrow{AD}$
On constate que $AMK\ $ et $\ ABC$ sont deux triangles en situation de Thalès donc, en appliquant le théorème de Thalès, on obtient :
$$\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{MK}}{\overline{BC}}\qquad(1)$$
Or, $\overrightarrow{AM}=k\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}=2\overrightarrow{AD}$
$\begin{array}{rcl}\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{MK}}{\overline{BC}}&\Leftrightarrow&\dfrac{k\overline{AB}}{\overline{AB}}=\dfrac{\overline{MK}}{2\overline{AD}}\\ \\&\Leftrightarrow&\dfrac{\overline{MK}}{2\overline{AD}}=k\\ \\&\Leftrightarrow&\overline{MK}=2k\overline{AD}\end{array}$
De plus $(MK)$ parallèle à $(BC)$ qui est parallèle à $(AD)$ donc, $(MK)$ est parallèle à $(AD)$
Ainsi, $\overline{MK}=2k\overline{AD}\ $ et $\ (MK)$ est parallèle à $(AD)$ telles que $[MK)\ $ et $\ [AD)$ orientées dans le même sens.
Par ailleurs, on a : $\overrightarrow{MK}+\overrightarrow{KN}=\overrightarrow{MN}$
Considérons $E$ le projeté de $D$ sur $(BC)$ parallèlement à $(AB)$ et $L$ le projeté de $M$ sur $(DE)$ parallèlement à $(BC)$
Or, $\overrightarrow{ML}=\overrightarrow{AD}$ donc, $\overline{ML}=\overline{AD}$
$$\dfrac{\overline{DL}}{\overline{DE}}=\dfrac{\overline{LN}}{\overline{EC}}\qquad(2)$$
Comme $\overline{DL}=\overline{AM}=k\overline{AB}\;;\ \overline{DE}=\overline{AB}\ $ et $\ \overline{EC}=\dfrac{1}{2}\overline{BC}=\overline{AD}$ alors, en remplaçant dans (2), on obtient :
$\begin{array}{rcl}\dfrac{\overline{DL}}{\overline{DE}}=\dfrac{\overline{LN}}{\overline{EC}}&\Leftrightarrow&\dfrac{k\overline{AB}}{\overline{AB}}=\dfrac{\overline{LN}}{\overline{AD}}\\ \\&\Leftrightarrow&\dfrac{\overline{LN}}{\overline{AD}}=k\\ \\&\Leftrightarrow&\overline{LN}=k\overline{AD}\end{array}$
Par ailleurs, comme $(LN)$ est parallèle à $(AD)$ avec $[LN)\ $ et $\ [AD)$ orientées dans le même sens alors, on peut conclure que $\overrightarrow{LN}=k\overrightarrow{AD}$
avec, $\overrightarrow{ML}=\overrightarrow{AD}\ $ et $\ \overrightarrow{LN}=k\overrightarrow{AD}$
$\begin{array}{rcl}\overrightarrow{NK}&=&\overrightarrow{MK}-\overrightarrow{MN}\\\\&=&2k\overrightarrow{AD}-(\overrightarrow{AD}+k\overrightarrow{AD})\\\\&=&(2k-k-1)\overrightarrow{AD}\\\\&=&(k-1)\overrightarrow{AD}\end{array}$
$K$ milieu de $[MN]$ si, et seulement si, $\overrightarrow{MK}+\overrightarrow{NK}=\vec{0}$
$\begin{array}{rcl}\overrightarrow{MK}+\overrightarrow{NK}=\vec{0}&\Leftrightarrow&2k\overrightarrow{AD}+(k-1)\overrightarrow{AD}=\vec{0}\\ \\&\Leftrightarrow&(2k+k-1)\overrightarrow{AD}=\vec{0}\quad\text{or, }\ \overrightarrow{AD}\neq\vec{0}\\ \\&\Leftrightarrow&3k-1=0\\ \\&\Leftrightarrow&k=\dfrac{1}{3}\end{array}$
Déterminons le réel $k$ pour que $\overrightarrow{MN}=\dfrac{3}{2}\overrightarrow{AD}$
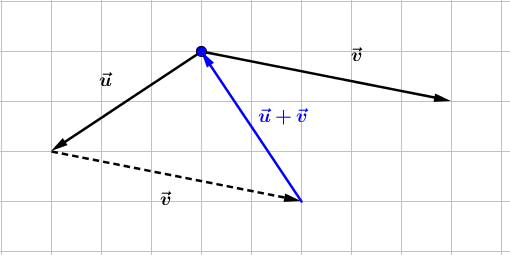
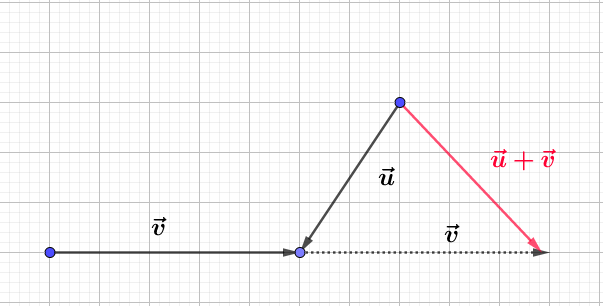
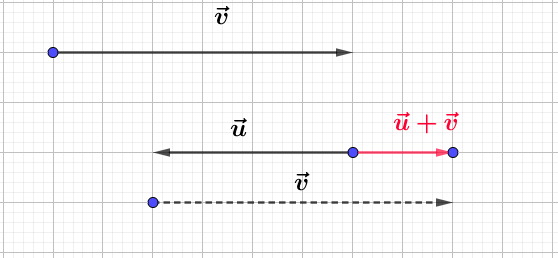
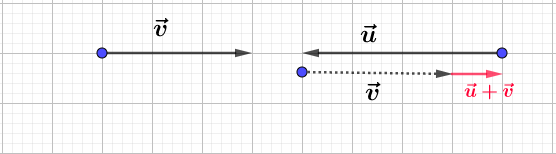
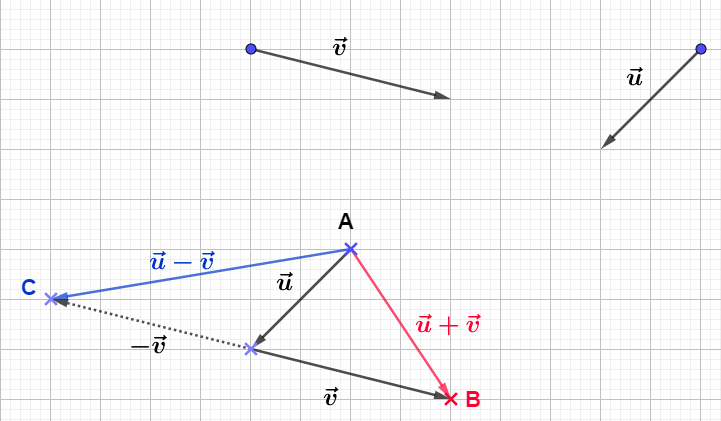
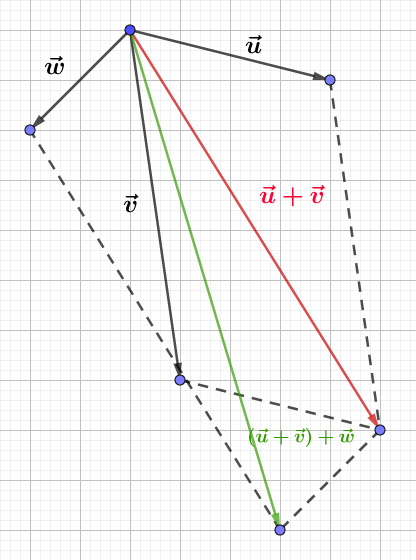
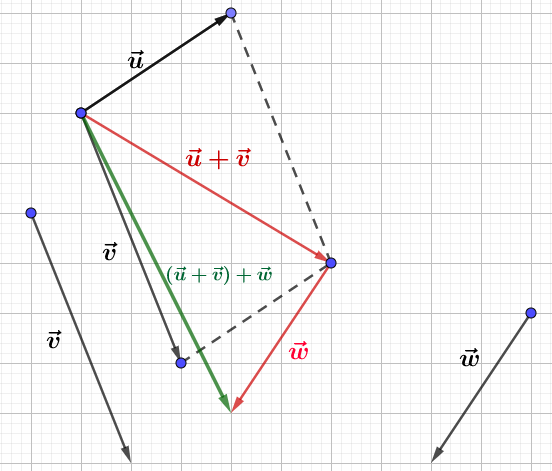
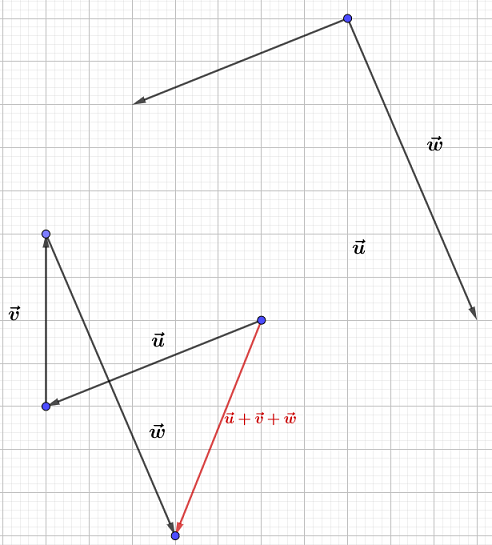
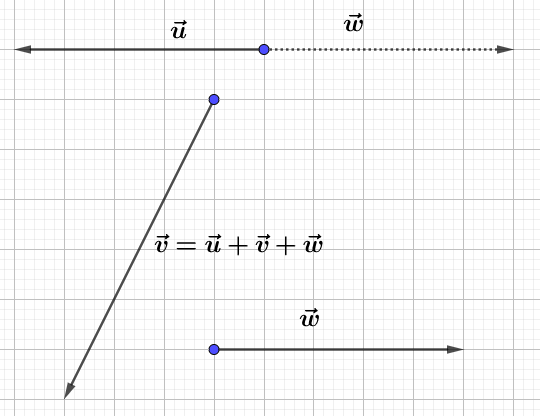
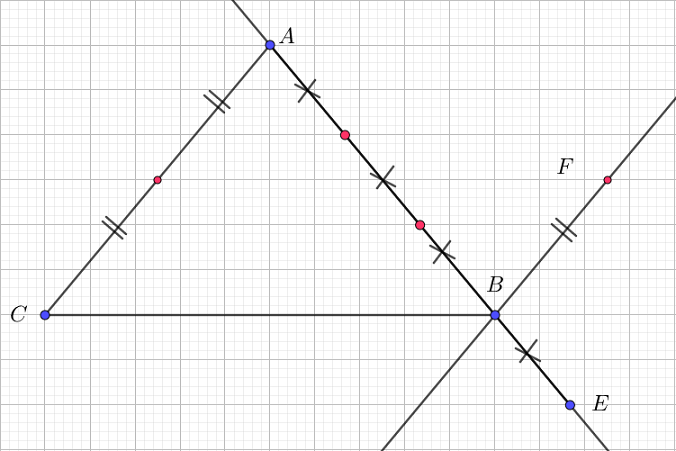
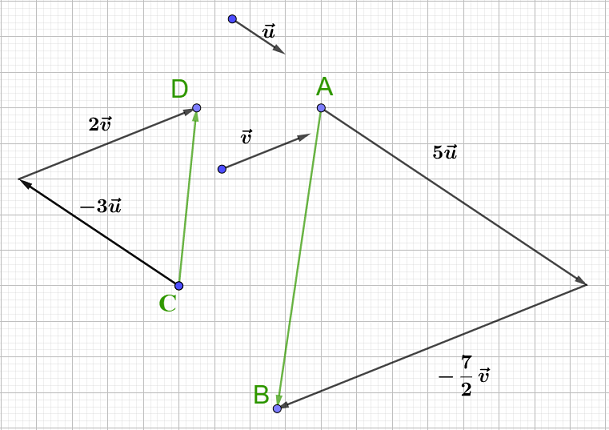
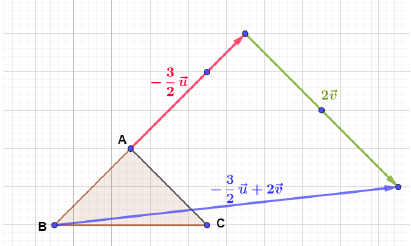
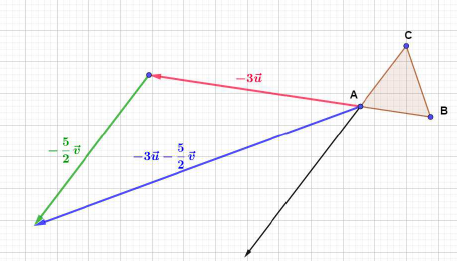
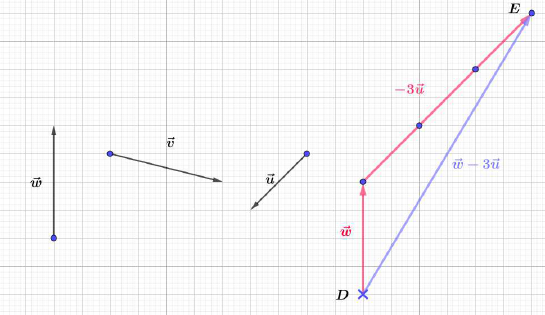
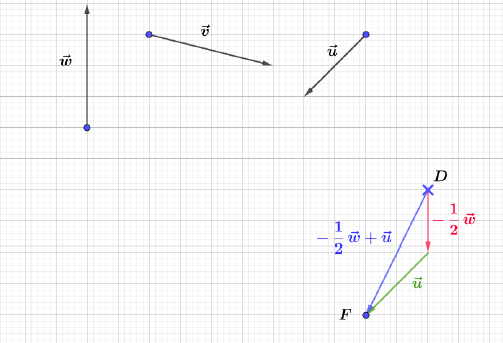
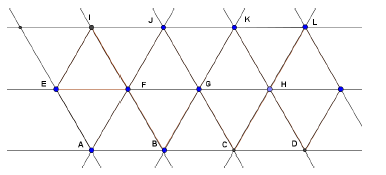
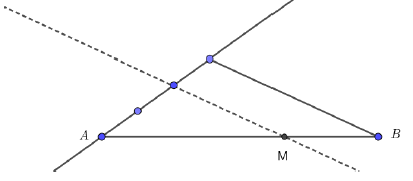






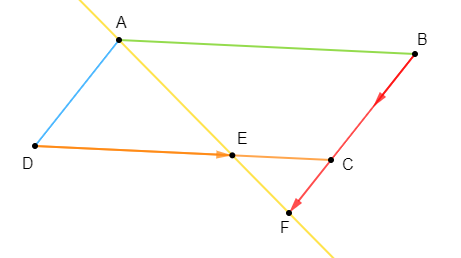

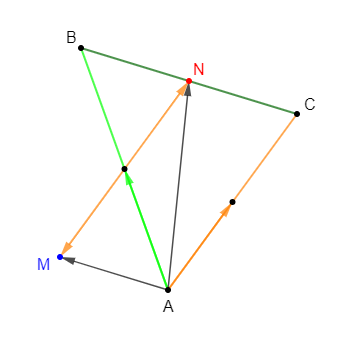


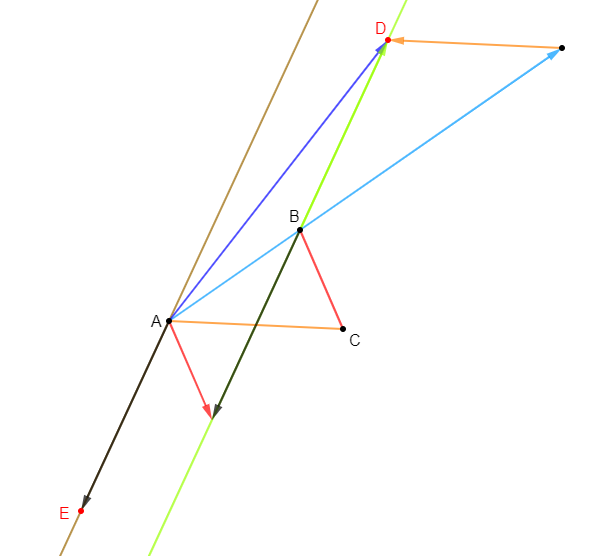
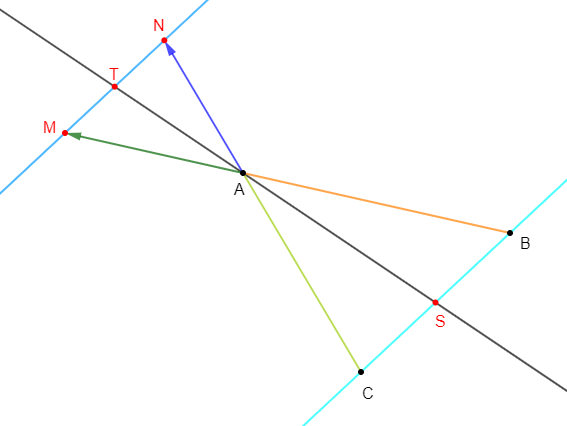
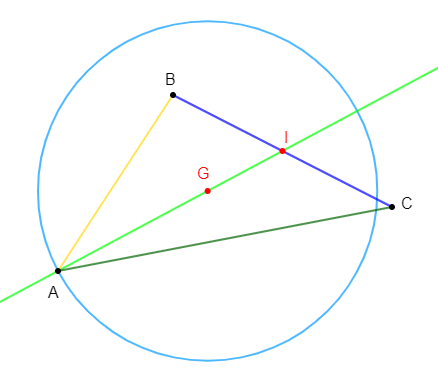
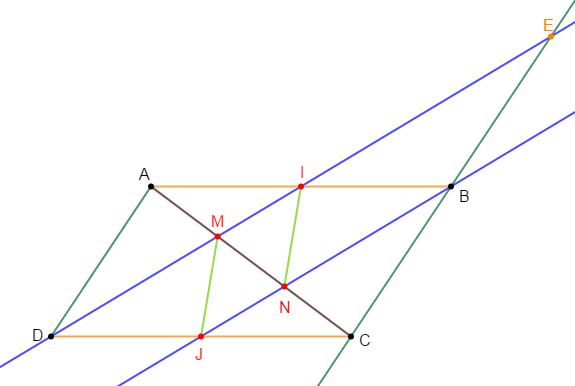
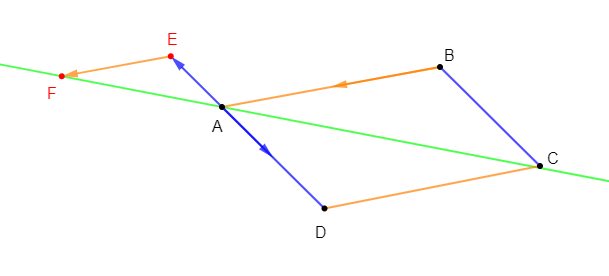
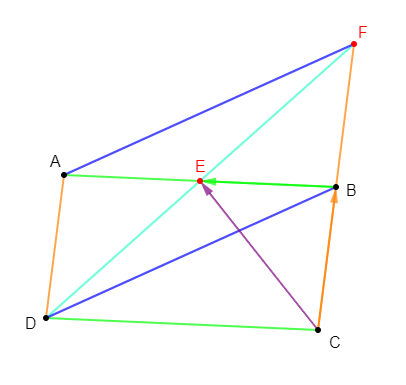
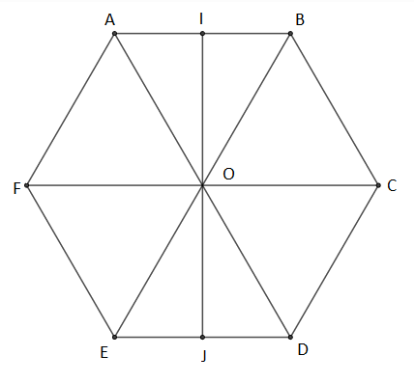
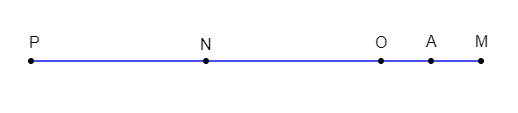
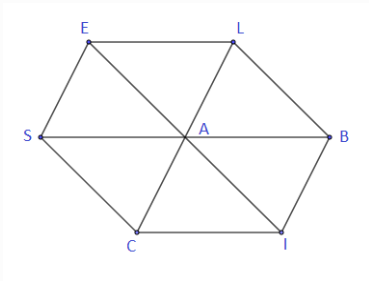
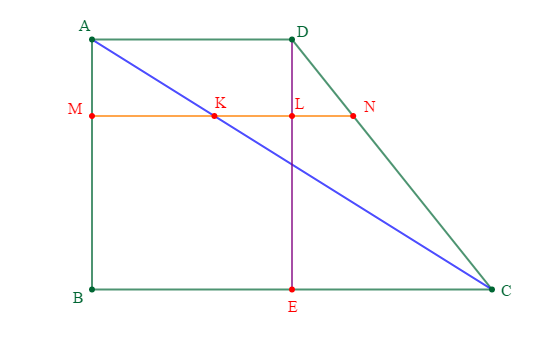
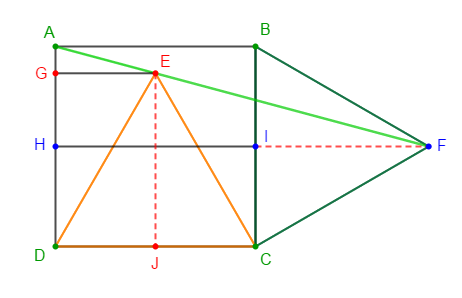

Commentaires
Anonyme (non vérifié)
mar, 01/29/2019 - 14:32
Permalien
pertinant
Anonyme (non vérifié)
dim, 10/04/2020 - 20:40
Permalien
Merci
Anonyme 23 (non vérifié)
mer, 12/16/2020 - 22:25
Permalien
Demande d aide
Anonyme (non vérifié)
sam, 01/09/2021 - 16:35
Permalien
Bien fait
Anonyme (non vérifié)
mar, 01/12/2021 - 22:11
Permalien
Intéressant.
Anonyme (non vérifié)
sam, 01/16/2021 - 14:05
Permalien
j'aimerais bien voir la
Anonyme (non vérifié)
mer, 01/20/2021 - 22:03
Permalien
Intéressant
Modou Diouf (non vérifié)
ven, 01/22/2021 - 00:04
Permalien
J ai besoin de la correction
HYACINTH A.B.MENDY (non vérifié)
mer, 01/27/2021 - 09:04
Permalien
Plus d'exercices merci.
Thiam (non vérifié)
mer, 01/27/2021 - 17:42
Permalien
Bonjour. J aurais besoin de
sqmqne (non vérifié)
mer, 02/03/2021 - 22:19
Permalien
la correction de l'exercice
Moussa ba (non vérifié)
jeu, 12/30/2021 - 16:27
Permalien
Correction des exercices
Anonyme (non vérifié)
sam, 11/19/2022 - 21:38
Permalien
J'ai besoin de la correction
Ndeye awa niang (non vérifié)
dim, 11/20/2022 - 12:30
Permalien
J'ai besoinde de la
maimouna diedhiou (non vérifié)
lun, 12/12/2022 - 23:27
Permalien
j'ai besoin la correction de
Mame Diarra (non vérifié)
lun, 12/26/2022 - 14:16
Permalien
J'aurais besoin la correction de l'exo 46
Salamoun (non vérifié)
sam, 02/04/2023 - 14:01
Permalien
J aurais besoin
Diallo (non vérifié)
mar, 12/12/2023 - 20:46
Permalien
Correction de exercices 36
Salamoun (non vérifié)
sam, 02/04/2023 - 14:01
Permalien
J aurais besoin
Salamoun (non vérifié)
sam, 02/04/2023 - 14:01
Permalien
J aurais besoin
Anonyme (non vérifié)
lun, 09/25/2023 - 22:16
Permalien
Cool
Anonyme (non vérifié)
lun, 09/25/2023 - 22:17
Permalien
Cool
Ndeye Fatou diop (non vérifié)
jeu, 12/14/2023 - 21:26
Permalien
J'ai besoin la correction de
Ndeye Fatou diop (non vérifié)
jeu, 12/14/2023 - 21:26
Permalien
J'ai besoin la correction de
Ndeye Fatou diop (non vérifié)
jeu, 12/14/2023 - 21:26
Permalien
J'ai besoin la correction de
Anonyme (non vérifié)
mer, 11/20/2024 - 22:56
Permalien
Je ne vois pas la correction
Ajouter un commentaire