Solution des exercices : Organisation d'un calcul - 6e
Classe:
Sixième
Exercice 1
1) Calculons chacune des expressions en utilisant les schémas de calcul.
On a : $A=13.5-3.5+10-15$
Soit le schéma de calcul suivant :
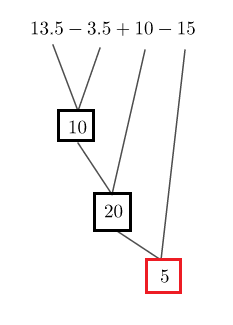
Donc, $\boxed{A=5}$
Soit : $B=100+20.5-70-0.5$
Le schéma de calcul est donné par :
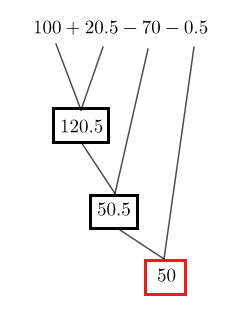
Ainsi, $\boxed{B=50}$
Soit : $C=265-15.5+110-28.5-30$
Considérons le schéma de calcul suivant :
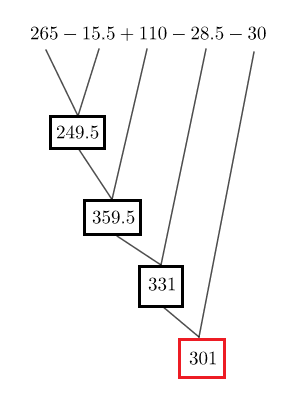
D'où, $\boxed{C=301}$
On a : $D=38.5-13.1+27.9-42.5-0.8$
Soit la schéma de calcul suivant :
Donc, $\boxed{D=10}$
Soit : $E=140.84+13.25-70.92-3.17$
Le schéma de calcul est donné par :
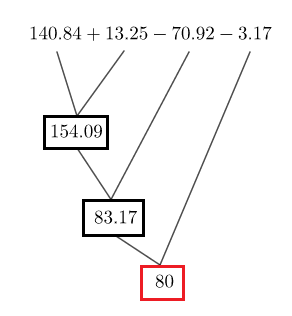
Par suite, $\boxed{E=80}$
2) Rangeons ces résultats dans l'ordre croissant.
On sait que : $5<10\;;\ 10<50\;;\ 50<80\ $ et $\ 80<301$
Donc, le rangement dans l'ordre croissant va donner :
$$5\;;\ 10\;;\ 50\;;\ 80\;;\ 301$$
Exercice 2
Calculons chacune des expressions en utilisant les schémas de calcul
Soit : $A=84:4\times 2$
Considérons le schéma de calcul suivant :
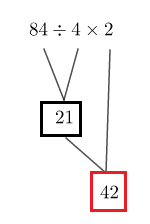
Donc, $\boxed{A=42}$
Soit : $B=42:6\times 8$
Le schéma de calcul est le suivant :
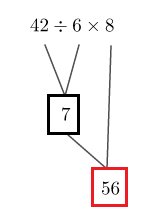
Ainsi, $\boxed{B=56}$
Soit : $C=38\times 2:19\times 5:3$ et soit le schéma de calcul suivant :
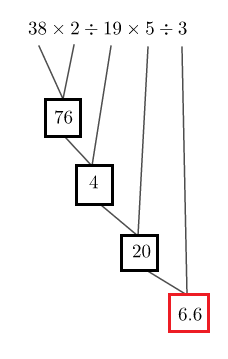
Alors, $\boxed{C=6.6}$
Soit : $D=5\times 7:4\times 100$
Considérons le schéma de calcul suivant :
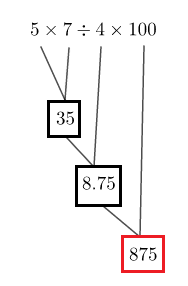
Donc, $\boxed{D=875}$
Exercice 3
1) Calculons en ligne chacune des expressions suivantes.
Soit : $P=1^{3}+2^{2}+3^{3}-4^{2}$ alors, on a :
$\begin{array}{rcl} P&=&1^{3}+2^{2}+3^{3}-4^{2}\\\\&=&1+4+27-16\\\\&=&16\end{array}$
Ainsi, $\boxed{P=16}$
Soit : $Q=7^{2}-6^{2}+2^{3}-3$ alors, on a :
$\begin{array}{rcl} Q&=&7^{2}-6^{2}+2^{3}-3\\\\&=&49-36+8-3\\\\&=&18\end{array}$
D'où, $\boxed{Q^=18}$
2) Comparons $P\ $ et $\ Q.$
On a : $P=16\ $ et $\ Q=18$
Or, $18>16$ donc, $Q$ est plus grand que $P.$
Exercice 4
Calculons en ligne chacune des expressions suivantes en utilisant les propriétés de la prioritaire.
Dans une suite d'opérations la multiplication et la division sont prioritaires sur l'addition et la soustraction.
Donc, dans les expressions suivantes, nous allons effectuer d'abord les multiplications et les divisions.
Soit : $I=5+4\times 3-8+18:9-6$
Alors, on effectue d'abord : $4\times 3=12\ $ et $\ 18:9=2$
Par suite,
$\begin{array}{rcl} I&=&5+4\times 3-8+18:9-6\\\\&=&5+12-8+2-6\\\\&=&5\end{array}$
Ainsi, $\boxed{I=5}$
Soit : $J=8.4-8.4:3+15+5\times 0.5$
On effectue d'abord : $8.4:3=2.8\ $ et $\ 5\times 0.5=2.5$
Puis, on obtient :
$\begin{array}{rcl} J&=&8.4-8.4:3+15+5\times 0.5\\\\&=&8.4-2.8+15+2.5\\\\&=&23.1\end{array}$
D'où, $\boxed{J=23.1}$
Soit : $K=121:11+55+2\times 3-28:4$
Donc, on effectue d'abord : $121:11=11\;;\ 2\times 3=6\ $ et $\ 28:4=7$
On obtient ensuite :
$\begin{array}{rcl} K&=&121:11+55+2\times 3-28:4\\\\&=&11+55+6-7\\\\&=&65\end{array}$
Ainsi, $\boxed{K=65}$
Soit : $L=35.5-5.2\times 5-14:2+6.1$
On effectue d'abord : $5.2\times 5=26\ $ et $\ 14:2=7$
Par suite,
$\begin{array}{rcl} L&=&35.5-5.2\times 5-14:2+6.1\\\\&=&35.5-26-7+6.1\\\\&=&8.6\end{array}$
D'où, $\boxed{L=8.6}$
Exercice 5
Calculons chacune des expressions en utilisant les schémas de calcul et les propriétés de la prioritaire.
Il faut noter que dans une suite d'opérations :
$-\ $ les opérations entre parenthèses sont prioritaires sur toute autre opération.
$-\ $ la multiplication et la division sont prioritaires sur l'addition et la soustraction.
Soit : $A=4.3+2\times[12-(7-13:2)]$
On effectue d'abord les opérations entre parenthèses ensuite, les multiplications et les divisions et enfin, le reste.
Soit alors le schéma de calcul suivant :
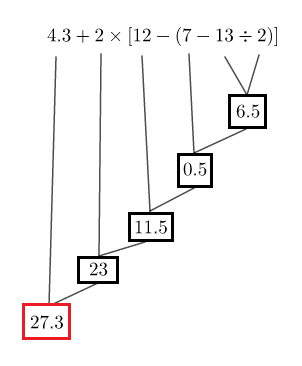
On obtient alors : $\boxed{A=27.3}$
Soit : $B=13.5-[8+(12.5:5-1.5)]$
On effectue d'abord les opérations entre parenthèses ensuite, les multiplications et les divisions et enfin, le reste.
Considérons le schéma de calcul suivant :
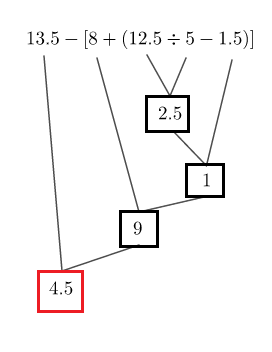
Ainsi, $\boxed{B=4.5}$
Soit : $C=[3.5+2\times(4.7-2.9)]\times 3+15:3-6.3$
De la même manière, on effectue d'abord les opérations entre parenthèses ensuite, les multiplications et les divisions et enfin, le reste.
Ainsi, on obtient le schéma de calcul suivant :
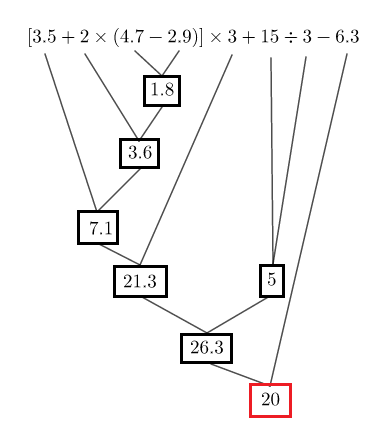
Par suite, $\boxed{C=20}$
Soit : $D=[13+5:2-(14-13)+12\times 3]$
En appliquant encore la même démarche, on obtient le schéma de calcul suivant :
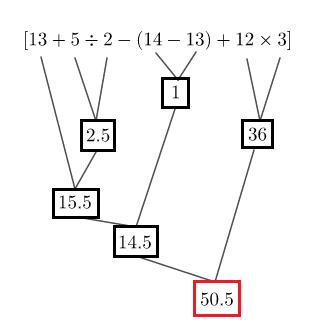
Ainsi, $\boxed{D=50.5}$
Auteur:
Diny Faye
Commentaires
Anonyme (non vérifié)
lun, 06/21/2021 - 23:59
Permalien
J'ai besoin du suite
Saly FAye (non vérifié)
jeu, 03/28/2024 - 19:49
Permalien
Toute les matière
fallou
lun, 05/09/2022 - 23:06
Permalien
Organisation de calcul
Anonyme (non vérifié)
jeu, 05/12/2022 - 11:53
Permalien
La solution
Anonyme (non vérifié)
lun, 04/17/2023 - 00:09
Permalien
Correction
Anonyme (non vérifié)
lun, 04/17/2023 - 00:09
Permalien
Correction
Saly FAye (non vérifié)
jeu, 03/28/2024 - 19:51
Permalien
La suite
Anonyme (non vérifié)
ven, 05/12/2023 - 05:13
Permalien
très bons exercices
Mame yande Diouf (non vérifié)
dim, 04/21/2024 - 12:22
Permalien
Demande de ne pas l'écrire seulement en chemz
Anonyme
mer, 05/08/2024 - 13:10
Permalien
Apprendre pour mieux servir
Anonyme (non vérifié)
mar, 05/14/2024 - 22:26
Permalien
espèce de médiocre
Anonyme (non vérifié)
ven, 06/14/2024 - 17:44
Permalien
solution des autres
Ajouter un commentaire