Vous êtes ici

Barycentre - 2nd

Classe:

Seconde

I. Définitions et propriétés

Activité

Sur une droite

$(D)$ muni d'un repère

$(A\;,\ \overrightarrow{AB})$ on donne les points

$C(4)\;,\ D(5)\;,\ E(9)$ et

$F(-4).$

Dans chacun des cas suivants trouver deux réels

$\alpha$ et

$\beta$ tels que :

$\alpha\overrightarrow{BA}+\beta\overrightarrow{BC}=\vec{0}$

$\alpha\overrightarrow{AD}+\beta\overrightarrow{AB}=\vec{0}$

$\alpha\overrightarrow{BD}+\beta\overrightarrow{BE}=\vec{0}$

Résolution

d'après le graphique on a :

$3\overrightarrow{BA}+\overrightarrow{BC}=\vec{0}$ donc,

$\alpha=3$ et

$\beta=1$

$\overrightarrow{AD}-5\overrightarrow{AB}=\vec{0}$ donc,

$\alpha=1$ et

$\beta=-5$

$2\overrightarrow{BD}-\overrightarrow{BE}=\vec{0}$ donc,

$\alpha=2$ et

$\beta=-1$

I.1 Définitions

$A$ et

$B$ deux points du plan,

$\alpha$ et

$\beta$ deux réels tels que

$\alpha+\beta\neq 0.$ Le barycentre de

$A$ et

$B$ affectés des coefficients respectifs

$\alpha$ et

$\beta$ est l'unique point

$G$ tel que

$\alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0}\quad\text{ou}\quad\alpha \overrightarrow{AG} +\beta \overrightarrow{BG} =\vec{0}$

On dit aussi que

$G$ est le barycentre des points pondérés

$(A\;;\ \alpha)$ et

$(B\;;\ \beta)$

Exercice d'application

Déterminer

$\alpha$ et

$\beta$ pour que

$A$ soit barycentre de

$(B\;;\ \alpha)$ et

$(C\;;\ \beta)$ dans les cas suivants :

$2\overrightarrow{AC}+3\overrightarrow{BA}=\vec{0}$

$\overrightarrow{AC}+3\overrightarrow{BC}=\vec{0}$

$\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{AB}$

Résolution

$2\overrightarrow{AC}+3\overrightarrow{BA}=\vec{0}\ \Rightarrow\ 2\overrightarrow{AC}-3\overrightarrow{AB}=\vec{0}$ donc

$A$ est barycentre de

$(B\;;\ -3)$ et

$(C\;;\ 2)$

$\begin{array}{rcl}\overrightarrow{AC}+3\overrightarrow{BC}=\vec{0}&\Leftrightarrow&\overrightarrow{AC}+3\overrightarrow{BA}+3\overrightarrow{AC}=\vec{0}\\ \\ &\Leftrightarrow&4\overrightarrow{AC}+3\overrightarrow{BA}=\vec{0}\\ \\ &\Leftrightarrow&4\overrightarrow{AC}-3\overrightarrow{AB}=\vec{0}\end{array}$

Donc,

$A$ est barycentre de

$(C\;;\ 4)$ et

$(C\;;\ -3)$

$\begin{array}{rcl}\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{AB}&\Leftrightarrow&3\overrightarrow{BC}=2\overrightarrow{AB}\\ \\&\Leftrightarrow&3\overrightarrow{BC}-2\overrightarrow{AB}=\vec{0}\\ \\&\Leftrightarrow&3\overrightarrow{BA}+3\overrightarrow{AC}-2\overrightarrow{AB}=\vec{0}\\ \\ &\Leftrightarrow&-5\overrightarrow{AB}+3\overrightarrow{AC}=\vec{0}\end{array}$

Donc,

$A$ est barycentre de

$(B\;;\ -5)$ et

$(C\;;\ 3)$

Remarques

$\centerdot\ \$ Si

$G$ est le barycentre de

$(A\;;\ \alpha)$ ,

$\ (B\;;\ \beta)$ alors,

$\alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0} \quad \Rightarrow \quad \alpha \overrightarrow{GA}=-\beta\overrightarrow{GB}$

D'où,

$A$ ,

$\ G$ et

$B$ sont alignés.

$\centerdot\ \$ Si

$\alpha=\beta$ alors on a :

$\begin{array}{rcl} \alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0} &\Rightarrow & \alpha \left(\overrightarrow{GA} +\overrightarrow{GB}\right) =\vec{0}\\ \\&\Rightarrow & \overrightarrow{GA} +\overrightarrow{GB} =\vec{0}\end{array}$

Donc,

$G$ est le milieu de

$[AB]$ .

$\centerdot\ \$ Si

$\alpha=\beta$ on dira que

$G$ est isobarycentre (même coefficient) de

$A$ et

$B$ , et

$G$ est le milieu de

$[AB].$

I.2 Construction du barycentre de deux points

Activité

Soit

$A$ et

$B$ deux points du plan tels que

$AB=4\;cm$ et

$M$ barycentre de

$(A\;;\ 2)\;,\ (B\;;\ 1).$

1) Exprimer

$\overrightarrow{AM}$ en fonction de

$\overrightarrow{AB}$ puis construire

$M.$

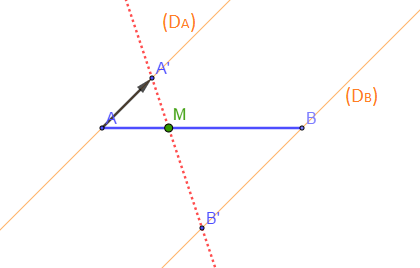
2) Placer deux points

$A$ et

$B$ tels que

$AB=4\;cm$ .

a) Tracer la droite

$(D_{A})$ passant par

$A$ et ne contenant pas

$B$ et

$(D_{B})$ la droite passant par

$B$ et parallèle à

$(D_{A}).$

Soit

$A'$ sur

$(D_{A})$ tel que

$\overrightarrow{AA}'=\vec{i}$ et

$B'\in(D_{B})$ tel que

$\overrightarrow{BB}'=-2\vec{i}.$

b) Montrer que

$M$ est le barycentre de

$(A\;;\ 2)$ et

$(B\;;\ 1)$ et aussi barycentre de

$(A'\;;\ 2)$ et

$(B'\;;\ 1).$

c) Construire

$M$ .

Résolution

$M$ barycentre de

$(A\;;\ 2)\;,\ (B\;;\ 1)$ donc,

$\begin{array}{rcl} 2\overrightarrow{AM}+\overrightarrow{BM}=\vec{0}&\Rightarrow&2\overrightarrow{AM}+\overrightarrow{BA}+\overrightarrow{AM}=\vec{0}\\ \\&\Rightarrow&3\overrightarrow{AM}=-\overrightarrow{BA}\\ \\&\Rightarrow&\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}\end{array}$

$M$ barycentre de

$(A\;;\ 2)\;,\ (B\;;\ 1)$ donc,

$\begin{array}{rcl} 2\overrightarrow{AM}+\overrightarrow{BM}=\vec{0}&\Rightarrow&2\overrightarrow{AA}'+2\overrightarrow{A'M}+\overrightarrow{BB}'+\overrightarrow{B'M}=\vec{0}\quad\text{or }\overrightarrow{BB}'=-2\overrightarrow{AA}'\\ \\ &\Rightarrow&2\overrightarrow{A'M}+\overrightarrow{B'M}=\vec{0}\end{array}$

D'où,

$M$ barycentre de

$(A'\;;\ 2)$ et

$(B'\;;\ 1)$

I.3 Propriétés

I.3.1 Homogénéité du barycentre

$G$ est le barycentre de

$(A;\ \alpha)$ ,

$\ (B;\ \beta)$ si, et seulement si,

$G$ est le barycentre de

$(A;\ k\alpha)$ et

$(B;\ k\beta)\;,\ \forall \: k\neq 0.$

Cela revient à dire que le barycentre reste inchangé si on multiplie ses coefficients par un même réel non nul.

Preuve

$\begin{array}{rcl} G \text{ barycentre de }(A; \alpha)\;,\ (B; \beta) &\Leftrightarrow & \alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0}\quad\text{avec }\alpha+\beta\neq 0\\ \\&\Leftrightarrow & k\left(\alpha \overrightarrow{GA} +\beta \overrightarrow{GB}\right) =\vec{0}\;;\ k\neq 0\;,\ k\alpha+k\beta\neq 0\\ \\ &\Leftrightarrow & (k\alpha) \overrightarrow{GA} +(k\beta) \overrightarrow{GB} =\vec{0}\end{array}$

I.3.2 Propriétés caractéristiques

$G$ barycentre de

$(A;\ \alpha)$ ,

$\ (B;\ \beta)$ alors

$\forall\;$

$M\in\mathcal{P}$ , on a :

$\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}=(\alpha + \beta)\overrightarrow{MG}\quad\text{avec }\ \alpha+\beta\neq 0$ ou encore

$\overrightarrow{MG}=\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}}{\alpha+\beta}$

Preuve

$G$ barycentre de

$(A;\ \alpha)$ ,

$\ (B;\ \beta)$ , montrons que

$\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}=(\alpha + \beta)\overrightarrow{MG}.$

$G$ barycentre de

$(A;\ \alpha)$ ,

$\ (B;\ \beta)$ si, et seulement si,

$\alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0}$ avec

$\alpha+\beta\neq 0.$

On a :

$\begin{array}{rcl} \alpha\overrightarrow{MA}+\beta\overrightarrow{MB}&=&\alpha\left(\overrightarrow{MG}+\overrightarrow{GA}\right)+\beta\left(\overrightarrow{MG}+\overrightarrow{GB}\right)\\ \\&=&(\alpha+\beta)\overrightarrow{MG}+\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}\\ \\&=& (\alpha+\beta)\overrightarrow{MG}+\vec{0}\quad\text{car}\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}=\vec{0}\end{array}$

du fait que

$G$ est le barycentre du système

$(A;\ \alpha)$ ,

$\ (B;\ \beta)$

Réciproquement, supposons

$\forall\;$

$M\in\mathcal{P}$ ,

$\ \alpha\overrightarrow{MA}+\beta\overrightarrow{MB}=(\alpha+\beta)\overrightarrow{MG}$ et que

$\alpha+\beta\neq 0$

On a :

$\begin{array}{rcl}\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}&=&\alpha\overrightarrow{MG}+\alpha\overrightarrow{GA}+\beta\overrightarrow{MG}+\beta\overrightarrow{GB}\\ \\&=&(\alpha+\beta)\overrightarrow{MG}+\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}\\ \\&=&(\alpha+\beta)\overrightarrow{MG} \end{array}$

Donc,

$\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}=\vec{0}$

D'où,

$G$ barycentre de

$(A;\ \alpha)$ ,

$\ (B;\ \beta)$

I.4 Coordonnées du barycentre

$G$ barycentre du système

$(A;\ \alpha)$ ,

$\ (B;\ \beta)$ alors,

$\begin{array}{rcl}\forall\;M\in\mathcal{P}\;,\ \alpha\overrightarrow{MA}+\beta\overrightarrow{MB}&=&(\alpha+\beta)\overrightarrow{MG}\\ \\ \Rightarrow\qquad \overrightarrow{MG}&=&\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}}{\alpha+\beta}\end{array}$

Dans le plan muni du repère

$(O;\ \vec{i},\ \vec{j})$ , on a :

$\overrightarrow{OG}=\dfrac{\alpha\overrightarrow{OA}+\beta\overrightarrow{OB}}{\alpha+\beta}$

Donc,

$G$ a pour coordonnées :

$x_{G}=\dfrac{\alpha.x_{A}+\beta.x_{B}}{\alpha+\beta}$

$y_{G}=\dfrac{\alpha.y_{A}+\beta.y_{B}}{\alpha+\beta}$

I.5 Réduction de $\vec{v}=\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}$

$\centerdot\ \$ Si

$\alpha+\beta\neq 0$ alors, le système

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ admet un barycentre. Soit

$G$ ce barycentre.

On a :

$\begin{array}{rcl}\vec{v}&=&\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}\\ \\&=&(\alpha+\beta)\overrightarrow{MG}\end{array}$

$\centerdot\ \ \alpha+\beta=0$ , le système

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ n'admet pas de barycentre.

On a alors :

$\begin{array}{rcl}\vec{v}&=&\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}\\ \\&=&\alpha\overrightarrow{MA}+\beta\overrightarrow{MA}+\beta\overrightarrow{AB}\\ \\&=&(\alpha+\beta)\overrightarrow{MA}+\beta\overrightarrow{AB}\end{array}$

Donc,

$\vec{v}=\beta\overrightarrow{AB}$ est un vecteur constant (ou indépendant de

$M$ ).

II. Barycentre de trois points

II.1 Définitions

Soient

$A$ ,

$\ B$ et

$C$ trois points du plan, affectés des coefficients

$\alpha$ ,

$\ \beta$ et

$\gamma$ ; des réels. On dit que

$G$ est le barycentre de

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ ,

$\ (C,\ \gamma)$ avec

$\alpha + \beta + \gamma \neq 0$ si :

$\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}=\vec{0}$

$G$ est unique.

Expérience

1) Soit

$ABCD$ un parallélogramme, déterminer

$\alpha\;,\ \beta$ et

$\gamma$ pour que

$D$ soit barycentre de

$(A\;;\ \alpha);,\ (B\;;\ \beta)$ et

$(C\;;\ \gamma).$

2) Soit

$\overrightarrow{AB}-2\overrightarrow{BC}+\overrightarrow{CD}=\vec{0}$ , déterminer

$b\;,\ c$ et

$d$ pour que

$A$ soit barycentre de

$(B\;;\ b);,\ (C\;;\ c)$ et

$(D\;;\ d).$

Résolution

$\begin{array}{rcl} ABCD\ \text{ parallélogramme }&\Rightarrow&\overrightarrow{AB}=\overrightarrow{DC}\\ \\ &\Rightarrow&\overrightarrow{AD}+\overrightarrow{DB}-\overrightarrow{DC}=\vec{0}\\ \\ &\Rightarrow&-\overrightarrow{DA}+\overrightarrow{DB}-\overrightarrow{DC}=\vec{0}\end{array}$

Donc,

$D$ est bien barycentre de

$(A\;;\ -1);,\ (B\;;\ 1)$ et

$(C\;;\ -1).$

$\begin{array}{rcl}\overrightarrow{AB}-2\overrightarrow{BC}+\overrightarrow{CD}=\vec{0}&\Rightarrow&\overrightarrow{AB}-2\overrightarrow{BA}-2\overrightarrow{AC}+\overrightarrow{CA}+\overrightarrow{AD}=\vec{0}\\ \\&\Rightarrow&3\overrightarrow{AB}-3\overrightarrow{AC}+\overrightarrow{AD}=\vec{0}\end{array}$

D'où,

$A$ est barycentre de

$(B\;;\ 3);,\ (C\;;\ -3)$ et

$(D\;;\ 1).$

II.2 Remarques

$G$ est le barycentre du système

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ ,

$\ (C,\ \gamma)$ . Si

$\alpha = \beta = \gamma$ on dira que

$G$ est isobarycentre de

$A$ ,

$\ B$ et

$C$ .

On a donc

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$
Ainsi,

$G$ est centre de gravité du triangle

$ABC.$

II.3 Propriétés

II.3.1 Homogénéité

$G$ est le barycentre du système

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ ,

$\ (C,\ \gamma)$ si, et seulement si,

$\forall\;k\neq 0\;,\ G$ est barycentre de

$(A,\ k\alpha)$ ,

$\ (B,\ k\beta)$ ,

$\ (C,\ k\gamma).$

Le barycentre reste inchangé si on multiplie les coefficients par un réel non nul.

II.3.2 Propriétés caractéristiques

$G$ est le barycentre du système

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ ,

$\ (C,\ \gamma)$ si, et seulement si,

$\forall\;M\in\mathcal{P}\;,\quad\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}=(\alpha+\beta+\gamma)\overrightarrow{MG}$

Par suite,

$\overrightarrow{MG}=\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}}{\alpha+\beta+\gamma}$

II.3.3 Associativité du barycentre

$G$ est le barycentre de

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ ,

$\ (C,\ \gamma)$ et si

$I$ est le barycentre de

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ alors,

$G$ est le barycentre de

$(I,\ \alpha+\beta)$ ,

$\ (C,\ \gamma).$

Preuve

$G$ barycentre de

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ ,

$\ (C,\ \gamma)$ alors,

$\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}=\vec{0}$ avec

$\alpha + \beta + \gamma \neq 0$

Donc,

$\begin{array}{rcl}\alpha\left(\overrightarrow{GI}+\overrightarrow{IA}\right)+\beta\left(\overrightarrow{GI}+\overrightarrow{IB}\right)+\gamma\overrightarrow{GC} = \vec{0}&\Rightarrow&\alpha\overrightarrow{GI}+\alpha\overrightarrow{IA}+\beta\overrightarrow{GI}+\beta\overrightarrow{IB}+\gamma\overrightarrow{GC} = \vec{0} \\ \\ &\Rightarrow&(\alpha+\beta)\overrightarrow{GI}+\alpha\overrightarrow{IA}+\beta\overrightarrow{IB}+\gamma\overrightarrow{GC} = \vec{0} \end{array}$

Or,

$I$ est le barycentre de

$(A,\ \alpha)$ ,

$\ (B, \beta)$ donc,

$\alpha\overrightarrow{IA}+\beta\overrightarrow{IB}=\vec{0}.$

Par suite,

$\ (\alpha+\beta)\overrightarrow{GI}+\gamma\overrightarrow{GC}=\vec{0}$ avec

$(\alpha + \beta) + \gamma \neq 0$

D'où,

$G$ est barycentre de

$(I,\ (\alpha+\beta))$ ,

$\ (C,\ \gamma).$

II.4 Coordonnées du barycentre

$G$ barycentre du système

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ ,

$\ (C,\ \gamma).$

On a :

$\begin{array}{rcl}\forall\;M\in\mathcal{P}\;,\ \alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}&=&(\alpha+\beta+\gamma)\overrightarrow{MG}\\ \\ \Rightarrow\qquad \overrightarrow{MG}&=&\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}}{\alpha+\beta+\gamma}\end{array}$

Dans le plan muni du repère

$(O;\ \vec{i},\ \vec{j})$ , pour

$M=O$ on a :

$\overrightarrow{OG}=\dfrac{\alpha\overrightarrow{OA}+\beta\overrightarrow{OB}+\gamma\overrightarrow{OC}}{\alpha+\beta+\gamma}$

Donc,

$G$ a pour coordonnées :

$x_{G}=\dfrac{\alpha.x_{A}+\beta.x_{B}+\gamma.x_{C}}{\alpha+\beta+\gamma}$

$y_{G}=\dfrac{\alpha.y_{A}+\beta.y_{B}+\gamma.y_{C}}{\alpha+\beta+\gamma}$

Dans le repère

$\left(A;\ \overrightarrow{AB},\ \overrightarrow{AC}\right)$ on a :

$\overrightarrow{AG}=\dfrac{\beta\overrightarrow{AB}+\gamma\overrightarrow{AC}}{\alpha+\beta+\gamma}$

Donc,

$G$ aura pour coordonnées :

$x_{G}=\dfrac{\beta}{\alpha+\beta+\gamma}$

$y_{G}=\dfrac{\gamma}{\alpha+\beta+\gamma}$

II.5 Ensemble de points

$A$ ,

$B$ et

$C$ trois points non alignés du plan

$\mathcal{P}.$

$\centerdot\ \ \mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ ||\overrightarrow{AM}||=k>0\right\rbrace$ est le cercle de centre

$A$ et de rayon

$k$ noté

$\mathcal{C}(A\;,\ k).$

$\centerdot\ \ \mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ ||\overrightarrow{MB}||=||\overrightarrow{MC}||\right\rbrace$ est la médiatrice du segment

$[BC].$

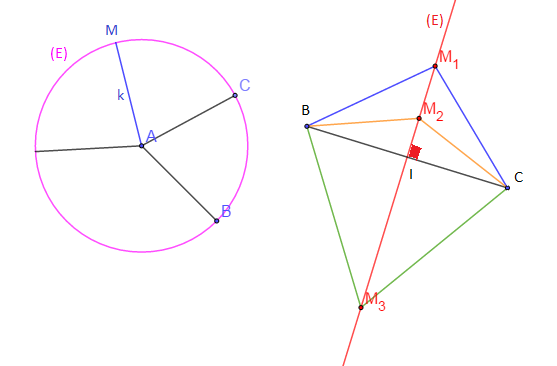
Exercice d'application

Soit un triangle

$ABC$ tel que

$AB=6\;cm\;,\ BC=4\;cm\;,\ AC=5\;cm$

1) Construire

$I$ et

$J$ tels que

$I$ soit barycentre de

$(A\;;\ 1)\;,\ (B\;;\ 1)$ et

$(C\;;\ 2)$ ,

$J$ barycentre de

$(A\;;\ 2)\;,\ (B\;;\ 3)$ et

$(C\;;\ -1).$

2) Déterminer l'ensemble

$E_{1}$ des points

$M$ tels que

$||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}||$

3) Déterminer l'ensemble

$E_{2}$ des points

$M$ tels que

$||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||\overrightarrow{MB}-\overrightarrow{MC}||$

Résolution

$\overrightarrow{IA}+\overrightarrow{IB}+2\overrightarrow{IC}=\vec{0}$ , considérons

$K$ barycentre de

$(A\;;\ 1)\;,\ (B\;;\ 1).$

$\alpha=\beta$ donc

$K$ est milieu de

$[AB]$ , d'où

$I$ barycentre de

$(K\;;\ 2)\;,\ (C\;;\ 2)$ donc

$I$ est milieu de

$[KC].$

$2\overrightarrow{JA}+3\overrightarrow{JB}-\overrightarrow{JC}=\vec{0}$ , considérons

$D$ barycentre de

$(B\;;\ 3)\;,\ (C\;;\ -1)$ alors,

$\begin{array}{rcl} 3\overrightarrow{DB}-\overrightarrow{DC}=\vec{0}&\Rightarrow&3\overrightarrow{DB}-\overrightarrow{DB}-\overrightarrow{BC}=\vec{0}\\ \\ &\Rightarrow&2\overrightarrow{DB}=\overrightarrow{BC}\\ \\ &\Rightarrow&\overrightarrow{DB}=\dfrac{1}{2}\overrightarrow{BC}\end{array}$

Donc,

$D$ est milieu de

$[BC]$

Par suite,

$J$ est barycentre de

$(A\;;\ 2)\;,\ (D\;;\ 2).$

D'où,

$J$ est milieu de

$[AD].$

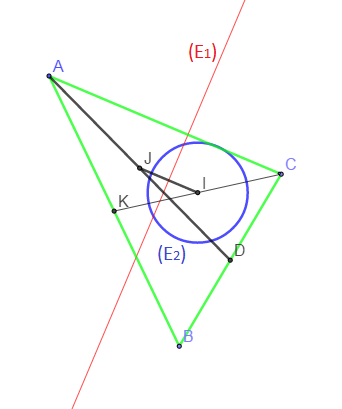
2) Déterminons l'ensemble des points

$M$ tels que

$||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}||$

$I$ barycentre de

$(A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 2)$ et

$J$ barycentre de

$(A\;;\ 2)\;,\ (B\;;\ 3)\;,\ (C\;;\ -1)$ alors,

$\begin{array}{rcl} ||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}||&\Leftrightarrow&||4\overrightarrow{MI}||=||4\overrightarrow{MJ}||\\ \\ &\Leftrightarrow&||\overrightarrow{MI}||=||\overrightarrow{MJ}||\end{array}$

Donc,

$E_{1}$ est la médiatrice de

$[IJ]$

3) Déterminons l'ensemble des points

$M$ tels que

$||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||\overrightarrow{MB}-\overrightarrow{MC}||$

$\begin{array}{rcl} ||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||\overrightarrow{MB}-\overrightarrow{MC}||&\Leftrightarrow&||4\overrightarrow{MI}||=||\overrightarrow{CM}+\overrightarrow{MB}||\\ \\ &\Leftrightarrow&||4\overrightarrow{MI}||=||\overrightarrow{CB}||\\ \\ &\Leftrightarrow&||\overrightarrow{MI}||=\dfrac{1}{4}||\overrightarrow{CB}||\end{array}$

Or,

$BC=4\;cm$ donc,

$E_{2}$ est le cercle de centre

$I$ et de rayon 1.

Auteur:

Diny Faye & Seyni Ndiaye