Vous êtes ici

Barycentre - 2nd

Classe:

Seconde

I. Définitions et propriétés

Activité

Sur une droite $(D)$ muni d'un repère $(A\;,\ \overrightarrow{AB})$ on donne les points $C(4)\;,\ D(5)\;,\ E(9)$ et $F(-4).$

Dans chacun des cas suivants trouver deux réels $\alpha$ et $\beta$ tels que :

a) $\alpha\overrightarrow{BA}+\beta\overrightarrow{BC}=\vec{0}$

b) $\alpha\overrightarrow{AD}+\beta\overrightarrow{AB}=\vec{0}$

c) $\alpha\overrightarrow{BD}+\beta\overrightarrow{BE}=\vec{0}$

Résolution

d'après le graphique on a :

a) $3\overrightarrow{BA}+\overrightarrow{BC}=\vec{0}$ donc, $\alpha=3$ et $\beta=1$

b) $\overrightarrow{AD}-5\overrightarrow{AB}=\vec{0}$ donc, $\alpha=1$ et $\beta=-5$

c) $2\overrightarrow{BD}-\overrightarrow{BE}=\vec{0}$ donc, $\alpha=2$ et $\beta=-1$

I.1 Définitions

$A$ et $B$ deux points du plan, $\alpha$ et $\beta$ deux réels tels que $\alpha+\beta\neq 0.$ Le barycentre de $A$ et $B$ affectés des coefficients respectifs $\alpha$ et $\beta$ est l'unique point $G$ tel que

$$\alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0}\quad\text{ou}\quad\alpha \overrightarrow{AG} +\beta \overrightarrow{BG} =\vec{0}$$

On dit aussi que $G$ est le barycentre des points pondérés $(A\;;\ \alpha)$ et $(B\;;\ \beta)$

Exercice d'application

Déterminer $\alpha$ et $\beta$ pour que $A$ soit barycentre de $(B\;;\ \alpha)$ et $(C\;;\ \beta)$ dans les cas suivants :

a) $2\overrightarrow{AC}+3\overrightarrow{BA}=\vec{0}$

b) $\overrightarrow{AC}+3\overrightarrow{BC}=\vec{0}$

c) $\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{AB}$

Résolution

a) $2\overrightarrow{AC}+3\overrightarrow{BA}=\vec{0}\ \Rightarrow\ 2\overrightarrow{AC}-3\overrightarrow{AB}=\vec{0}$ donc $A$ est barycentre de $(B\;;\ -3)$ et $(C\;;\ 2)$

b) $$\begin{array}{rcl}\overrightarrow{AC}+3\overrightarrow{BC}=\vec{0}&\Leftrightarrow&\overrightarrow{AC}+3\overrightarrow{BA}+3\overrightarrow{AC}=\vec{0}\\ \\ &\Leftrightarrow&4\overrightarrow{AC}+3\overrightarrow{BA}=\vec{0}\\ \\ &\Leftrightarrow&4\overrightarrow{AC}-3\overrightarrow{AB}=\vec{0}\end{array}$$

Donc, $A$ est barycentre de $(C\;;\ 4)$ et $(C\;;\ -3)$

c) $$\begin{array}{rcl}\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{AB}&\Leftrightarrow&3\overrightarrow{BC}=2\overrightarrow{AB}\\ \\&\Leftrightarrow&3\overrightarrow{BC}-2\overrightarrow{AB}=\vec{0}\\ \\&\Leftrightarrow&3\overrightarrow{BA}+3\overrightarrow{AC}-2\overrightarrow{AB}=\vec{0}\\ \\ &\Leftrightarrow&-5\overrightarrow{AB}+3\overrightarrow{AC}=\vec{0}\end{array}$$

Donc, $A$ est barycentre de $(B\;;\ -5)$ et $(C\;;\ 3)$

Remarques

$\centerdot\ \ $ Si $G$ est le barycentre de $(A\;;\ \alpha)$ , $\ (B\;;\ \beta)$ alors,

$\alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0} \quad \Rightarrow \quad \alpha \overrightarrow{GA}=-\beta\overrightarrow{GB}$

D'où, $A$, $\ G$ et $B$ sont alignés.

$\centerdot\ \ $ Si $\alpha=\beta$ alors on a :

$$\begin{array}{rcl} \alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0} &\Rightarrow & \alpha \left(\overrightarrow{GA} +\overrightarrow{GB}\right) =\vec{0}\\ \\&\Rightarrow & \overrightarrow{GA} +\overrightarrow{GB} =\vec{0}\end{array}$$

Donc, $G$ est le milieu de $[AB]$.

$\centerdot\ \ $ Si $\alpha=\beta$ on dira que $G$ est isobarycentre (même coefficient) de $A$ et $B$, et $G$ est le milieu de $[AB].$

I.2 Construction du barycentre de deux points

Activité

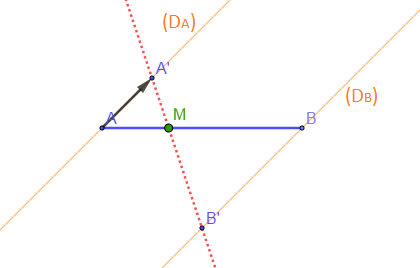
Soit $A$ et $B$ deux points du plan tels que $AB=4\;cm$ et $M$ barycentre de $(A\;;\ 2)\;,\ (B\;;\ 1).$

1) Exprimer $\overrightarrow{AM}$ en fonction de $\overrightarrow{AB}$ puis construire $M.$

2) Placer deux points $A$ et $B$ tels que $AB=4\;cm$.

a) Tracer la droite $(D_{A})$ passant par $A$ et ne contenant pas $B$ et $(D_{B})$ la droite passant par $B$ et parallèle à $(D_{A}).$

Soit $A'$ sur $(D_{A})$ tel que $\overrightarrow{AA}'=\vec{i}$ et $B'\in(D_{B})$ tel que $\overrightarrow{BB}'=-2\vec{i}.$

b) Montrer que $M$ est le barycentre de $(A\;;\ 2)$ et $(B\;;\ 1)$ et aussi barycentre de $(A'\;;\ 2)$ et $(B'\;;\ 1).$

c) Construire $M$.

Résolution

1) $M$ barycentre de $(A\;;\ 2)\;,\ (B\;;\ 1)$ donc, $$\begin{array}{rcl} 2\overrightarrow{AM}+\overrightarrow{BM}=\vec{0}&\Rightarrow&2\overrightarrow{AM}+\overrightarrow{BA}+\overrightarrow{AM}=\vec{0}\\ \\&\Rightarrow&3\overrightarrow{AM}=-\overrightarrow{BA}\\ \\&\Rightarrow&\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}\end{array}$$

2) $M$ barycentre de $(A\;;\ 2)\;,\ (B\;;\ 1)$ donc, $$\begin{array}{rcl} 2\overrightarrow{AM}+\overrightarrow{BM}=\vec{0}&\Rightarrow&2\overrightarrow{AA}'+2\overrightarrow{A'M}+\overrightarrow{BB}'+\overrightarrow{B'M}=\vec{0}\quad\text{or }\overrightarrow{BB}'=-2\overrightarrow{AA}'\\ \\ &\Rightarrow&2\overrightarrow{A'M}+\overrightarrow{B'M}=\vec{0}\end{array}$$

D'où, $M$ barycentre de $(A'\;;\ 2)$ et $(B'\;;\ 1)$

I.3 Propriétés

I.3.1 Homogénéité du barycentre

$G$ est le barycentre de $(A;\ \alpha)$ , $\ (B;\ \beta)$ si, et seulement si, $G$ est le barycentre de $(A;\ k\alpha)$ et $(B;\ k\beta)\;,\ \forall \: k\neq 0.$

Cela revient à dire que le barycentre reste inchangé si on multiplie ses coefficients par un même réel non nul.

Preuve

$$\begin{array}{rcl} G \text{ barycentre de }(A; \alpha)\;,\ (B; \beta) &\Leftrightarrow & \alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0}\quad\text{avec }\alpha+\beta\neq 0\\ \\&\Leftrightarrow & k\left(\alpha \overrightarrow{GA} +\beta \overrightarrow{GB}\right) =\vec{0}\;;\ k\neq 0\;,\ k\alpha+k\beta\neq 0\\ \\ &\Leftrightarrow & (k\alpha) \overrightarrow{GA} +(k\beta) \overrightarrow{GB} =\vec{0}\end{array}$$

I.3.2 Propriétés caractéristiques

$G$ barycentre de $(A;\ \alpha)$ , $\ (B;\ \beta)$ alors $\forall\;$ $M\in\mathcal{P}$, on a : $$\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}=(\alpha + \beta)\overrightarrow{MG}\quad\text{avec }\ \alpha+\beta\neq 0$$ ou encore

$$\overrightarrow{MG}=\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}}{\alpha+\beta}$$

Preuve

$G$ barycentre de $(A;\ \alpha)$, $\ (B;\ \beta)$, montrons que $\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}=(\alpha + \beta)\overrightarrow{MG}.$

$G$ barycentre de $(A;\ \alpha)$, $\ (B;\ \beta)$ si, et seulement si, $\alpha \overrightarrow{GA} +\beta \overrightarrow{GB} =\vec{0}$ avec $\alpha+\beta\neq 0.$

On a :

$$\begin{array}{rcl} \alpha\overrightarrow{MA}+\beta\overrightarrow{MB}&=&\alpha\left(\overrightarrow{MG}+\overrightarrow{GA}\right)+\beta\left(\overrightarrow{MG}+\overrightarrow{GB}\right)\\ \\&=&(\alpha+\beta)\overrightarrow{MG}+\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}\\ \\&=& (\alpha+\beta)\overrightarrow{MG}+\vec{0}\quad\text{car}\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}=\vec{0}\end{array}$$

du fait que $G$ est le barycentre du système $(A;\ \alpha)$ , $\ (B;\ \beta)$

Réciproquement, supposons $\forall\;$ $M\in\mathcal{P}$, $\ \alpha\overrightarrow{MA}+\beta\overrightarrow{MB}=(\alpha+\beta)\overrightarrow{MG}$ et que $\alpha+\beta\neq 0$

On a :

$$\begin{array}{rcl}\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}&=&\alpha\overrightarrow{MG}+\alpha\overrightarrow{GA}+\beta\overrightarrow{MG}+\beta\overrightarrow{GB}\\ \\&=&(\alpha+\beta)\overrightarrow{MG}+\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}\\ \\&=&(\alpha+\beta)\overrightarrow{MG} \end{array}$$

Donc, $\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}=\vec{0}$

D'où, $G$ barycentre de $(A;\ \alpha)$ , $\ (B;\ \beta)$

I.4 Coordonnées du barycentre

$G$ barycentre du système $(A;\ \alpha)$ , $\ (B;\ \beta)$ alors,

$$\begin{array}{rcl}\forall\;M\in\mathcal{P}\;,\ \alpha\overrightarrow{MA}+\beta\overrightarrow{MB}&=&(\alpha+\beta)\overrightarrow{MG}\\ \\ \Rightarrow\qquad \overrightarrow{MG}&=&\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}}{\alpha+\beta}\end{array}$$

Dans le plan muni du repère $(O;\ \vec{i},\ \vec{j})$, on a : $\overrightarrow{OG}=\dfrac{\alpha\overrightarrow{OA}+\beta\overrightarrow{OB}}{\alpha+\beta}$

Donc, $G$ a pour coordonnées :

$$x_{G}=\dfrac{\alpha.x_{A}+\beta.x_{B}}{\alpha+\beta}$$

$$y_{G}=\dfrac{\alpha.y_{A}+\beta.y_{B}}{\alpha+\beta}$$

I.5 Réduction de $\vec{v}=\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}$

$\centerdot\ \ $ Si $\alpha+\beta\neq 0$ alors, le système $(A,\ \alpha)$, $\ (B,\ \beta)$ admet un barycentre. Soit $G$ ce barycentre.

On a :

$$\begin{array}{rcl}\vec{v}&=&\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}\\ \\&=&(\alpha+\beta)\overrightarrow{MG}\end{array}$$

$\centerdot\ \ \alpha+\beta=0$, le système $(A,\ \alpha)$, $\ (B,\ \beta)$ n'admet pas de barycentre.

On a alors :

$$\begin{array}{rcl}\vec{v}&=&\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}\\ \\&=&\alpha\overrightarrow{MA}+\beta\overrightarrow{MA}+\beta\overrightarrow{AB}\\ \\&=&(\alpha+\beta)\overrightarrow{MA}+\beta\overrightarrow{AB}\end{array}$$

Donc, $\vec{v}=\beta\overrightarrow{AB}$ est un vecteur constant (ou indépendant de $M$).

II. Barycentre de trois points

II.1 Définitions

Soient $A$, $\ B$ et $C$ trois points du plan, affectés des coefficients $\alpha$, $\ \beta$ et $\gamma$; des réels. On dit que $G$ est le barycentre de $(A,\ \alpha)$, $\ (B,\ \beta)$, $\ (C,\ \gamma)$ avec $\alpha + \beta + \gamma \neq 0$ si :

$$\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}=\vec{0}$$

$G$ est unique.

Expérience

1) Soit $ABCD$ un parallélogramme, déterminer $\alpha\;,\ \beta$ et $\gamma$ pour que $D$ soit barycentre de $(A\;;\ \alpha);,\ (B\;;\ \beta)$ et $(C\;;\ \gamma).$

2) Soit $\overrightarrow{AB}-2\overrightarrow{BC}+\overrightarrow{CD}=\vec{0}$, déterminer $b\;,\ c$ et $d$ pour que $A$ soit barycentre de $(B\;;\ b);,\ (C\;;\ c)$ et $(D\;;\ d).$

Résolution

1) $$\begin{array}{rcl} ABCD\ \text{ parallélogramme }&\Rightarrow&\overrightarrow{AB}=\overrightarrow{DC}\\ \\ &\Rightarrow&\overrightarrow{AD}+\overrightarrow{DB}-\overrightarrow{DC}=\vec{0}\\ \\ &\Rightarrow&-\overrightarrow{DA}+\overrightarrow{DB}-\overrightarrow{DC}=\vec{0}\end{array}$$

Donc, $D$ est bien barycentre de $(A\;;\ -1);,\ (B\;;\ 1)$ et $(C\;;\ -1).$

2) $$\begin{array}{rcl}\overrightarrow{AB}-2\overrightarrow{BC}+\overrightarrow{CD}=\vec{0}&\Rightarrow&\overrightarrow{AB}-2\overrightarrow{BA}-2\overrightarrow{AC}+\overrightarrow{CA}+\overrightarrow{AD}=\vec{0}\\ \\&\Rightarrow&3\overrightarrow{AB}-3\overrightarrow{AC}+\overrightarrow{AD}=\vec{0}\end{array}$$

D'où, $A$ est barycentre de $(B\;;\ 3);,\ (C\;;\ -3)$ et $(D\;;\ 1).$

II.2 Remarques

$G$ est le barycentre du système $(A,\ \alpha)$, $\ (B,\ \beta)$, $\ (C,\ \gamma)$. Si $\alpha = \beta = \gamma$ on dira que $G$ est isobarycentre de $A$, $\ B$ et $C$.

On a donc $$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$$
Ainsi, $G$ est centre de gravité du triangle $ABC.$

II.3 Propriétés

II.3.1 Homogénéité

$G$ est le barycentre du système $(A,\ \alpha)$, $\ (B,\ \beta)$, $\ (C,\ \gamma)$ si, et seulement si, $\forall\;k\neq 0\;,\ G$ est barycentre de $(A,\ k\alpha)$, $\ (B,\ k\beta)$, $\ (C,\ k\gamma).$

Le barycentre reste inchangé si on multiplie les coefficients par un réel non nul.

II.3.2 Propriétés caractéristiques

$G$ est le barycentre du système $(A,\ \alpha)$, $\ (B,\ \beta)$, $\ (C,\ \gamma)$ si, et seulement si, $$\forall\;M\in\mathcal{P}\;,\quad\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}=(\alpha+\beta+\gamma)\overrightarrow{MG}$$

Par suite, $$\overrightarrow{MG}=\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}}{\alpha+\beta+\gamma}$$

II.3.3 Associativité du barycentre

Si $G$ est le barycentre de $(A,\ \alpha)$, $\ (B,\ \beta)$, $\ (C,\ \gamma)$ et si $I$ est le barycentre de $(A,\ \alpha)$, $\ (B,\ \beta)$ alors, $G$ est le barycentre de $(I,\ \alpha+\beta)$, $\ (C,\ \gamma).$

Preuve

$G$ barycentre de $(A,\ \alpha)$, $\ (B,\ \beta)$, $\ (C,\ \gamma)$ alors, $\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}=\vec{0}$ avec $\alpha + \beta + \gamma \neq 0$

Donc,

$$\begin{array}{rcl}\alpha\left(\overrightarrow{GI}+\overrightarrow{IA}\right)+\beta\left(\overrightarrow{GI}+\overrightarrow{IB}\right)+\gamma\overrightarrow{GC} = \vec{0}&\Rightarrow&\alpha\overrightarrow{GI}+\alpha\overrightarrow{IA}+\beta\overrightarrow{GI}+\beta\overrightarrow{IB}+\gamma\overrightarrow{GC} = \vec{0} \\ \\ &\Rightarrow&(\alpha+\beta)\overrightarrow{GI}+\alpha\overrightarrow{IA}+\beta\overrightarrow{IB}+\gamma\overrightarrow{GC} = \vec{0} \end{array}$$

Or, $I$ est le barycentre de $(A,\ \alpha)$, $\ (B, \beta)$ donc, $\alpha\overrightarrow{IA}+\beta\overrightarrow{IB}=\vec{0}.$

Par suite, $\ (\alpha+\beta)\overrightarrow{GI}+\gamma\overrightarrow{GC}=\vec{0}$ avec $(\alpha + \beta) + \gamma \neq 0$

D'où, $G$ est barycentre de $(I,\ (\alpha+\beta))$, $\ (C,\ \gamma).$

II.4 Coordonnées du barycentre

$G$ barycentre du système $(A,\ \alpha)$, $\ (B,\ \beta)$, $\ (C,\ \gamma).$

On a :

$$\begin{array}{rcl}\forall\;M\in\mathcal{P}\;,\ \alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}&=&(\alpha+\beta+\gamma)\overrightarrow{MG}\\ \\ \Rightarrow\qquad \overrightarrow{MG}&=&\dfrac{\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}}{\alpha+\beta+\gamma}\end{array}$$

Dans le plan muni du repère $(O;\ \vec{i},\ \vec{j})$, pour $M=O$ on a :

$$\overrightarrow{OG}=\dfrac{\alpha\overrightarrow{OA}+\beta\overrightarrow{OB}+\gamma\overrightarrow{OC}}{\alpha+\beta+\gamma}$$

Donc, $G$ a pour coordonnées :

$$x_{G}=\dfrac{\alpha.x_{A}+\beta.x_{B}+\gamma.x_{C}}{\alpha+\beta+\gamma}$$

$$y_{G}=\dfrac{\alpha.y_{A}+\beta.y_{B}+\gamma.y_{C}}{\alpha+\beta+\gamma}$$

Dans le repère $\left(A;\ \overrightarrow{AB},\ \overrightarrow{AC}\right)$ on a : $$\overrightarrow{AG}=\dfrac{\beta\overrightarrow{AB}+\gamma\overrightarrow{AC}}{\alpha+\beta+\gamma}$$

Donc, $G$ aura pour coordonnées :

$$x_{G}=\dfrac{\beta}{\alpha+\beta+\gamma}$$

$$y_{G}=\dfrac{\gamma}{\alpha+\beta+\gamma}$$

II.5 Ensemble de points

$A$, $B$ et $C$ trois points non alignés du plan $\mathcal{P}.$

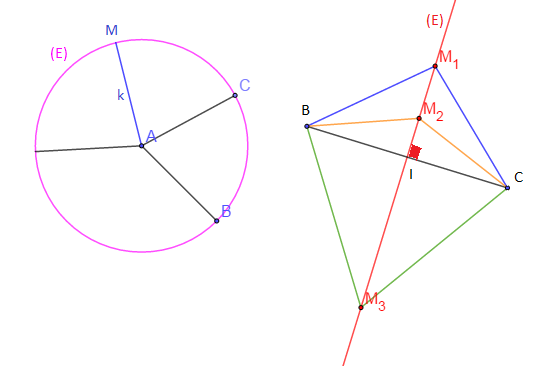
$\centerdot\ \ \mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ ||\overrightarrow{AM}||=k>0\right\rbrace$ est le cercle de centre $A$ et de rayon $k$ noté $\mathcal{C}(A\;,\ k).$

$\centerdot\ \ \mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ ||\overrightarrow{MB}||=||\overrightarrow{MC}||\right\rbrace$ est la médiatrice du segment $[BC].$

Exercice d'application

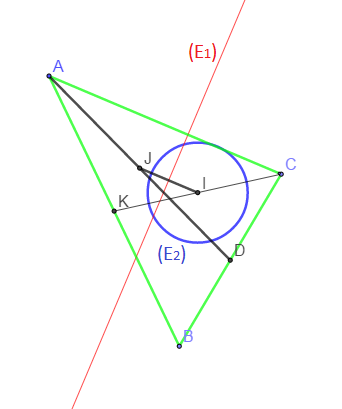
Soit un triangle $ABC$ tel que $AB=6\;cm\;,\ BC=4\;cm\;,\ AC=5\;cm$

1) Construire $I$ et $J$ tels que $I$ soit barycentre de $(A\;;\ 1)\;,\ (B\;;\ 1)$ et $(C\;;\ 2)$, $J$ barycentre de $(A\;;\ 2)\;,\ (B\;;\ 3)$ et $(C\;;\ -1).$

2) Déterminer l'ensemble $E_{1}$ des points $M$ tels que $$||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}||$$

3) Déterminer l'ensemble $E_{2}$ des points $M$ tels que $$||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||\overrightarrow{MB}-\overrightarrow{MC}||$$

Résolution

1) $\overrightarrow{IA}+\overrightarrow{IB}+2\overrightarrow{IC}=\vec{0}$, considérons $K$ barycentre de $(A\;;\ 1)\;,\ (B\;;\ 1).$

$\alpha=\beta$ donc $K$ est milieu de $[AB]$, d'où $I$ barycentre de $(K\;;\ 2)\;,\ (C\;;\ 2)$ donc $I$ est milieu de $[KC].$

$2\overrightarrow{JA}+3\overrightarrow{JB}-\overrightarrow{JC}=\vec{0}$, considérons $D$ barycentre de $(B\;;\ 3)\;,\ (C\;;\ -1)$ alors, $$\begin{array}{rcl} 3\overrightarrow{DB}-\overrightarrow{DC}=\vec{0}&\Rightarrow&3\overrightarrow{DB}-\overrightarrow{DB}-\overrightarrow{BC}=\vec{0}\\ \\ &\Rightarrow&2\overrightarrow{DB}=\overrightarrow{BC}\\ \\ &\Rightarrow&\overrightarrow{DB}=\dfrac{1}{2}\overrightarrow{BC}\end{array}$$

Donc, $D$ est milieu de $[BC]$

Par suite, $J$ est barycentre de $(A\;;\ 2)\;,\ (D\;;\ 2).$

D'où, $J$ est milieu de $[AD].$

2) Déterminons l'ensemble des points $M$ tels que $$||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}||$$

$I$ barycentre de $(A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 2)$ et $J$ barycentre de $(A\;;\ 2)\;,\ (B\;;\ 3)\;,\ (C\;;\ -1)$ alors, $$\begin{array}{rcl} ||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}||&\Leftrightarrow&||4\overrightarrow{MI}||=||4\overrightarrow{MJ}||\\ \\ &\Leftrightarrow&||\overrightarrow{MI}||=||\overrightarrow{MJ}||\end{array}$$

Donc, $E_{1}$ est la médiatrice de $[IJ]$

3) Déterminons l'ensemble des points $M$ tels que $$||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||\overrightarrow{MB}-\overrightarrow{MC}||$$

$$\begin{array}{rcl} ||\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}||=||\overrightarrow{MB}-\overrightarrow{MC}||&\Leftrightarrow&||4\overrightarrow{MI}||=||\overrightarrow{CM}+\overrightarrow{MB}||\\ \\ &\Leftrightarrow&||4\overrightarrow{MI}||=||\overrightarrow{CB}||\\ \\ &\Leftrightarrow&||\overrightarrow{MI}||=\dfrac{1}{4}||\overrightarrow{CB}||\end{array}$$

Or, $BC=4\;cm$ donc, $E_{2}$ est le cercle de centre $I$ et de rayon 1.

Auteur:

Diny Faye & Seyni Ndiaye