Vous êtes ici

Géométrie dans l'espace - T S1

I Détermination de droites et de plans

$\centerdot\ \$ Une droite

$\Delta$ de l'espace est entièrement déterminée par :

$-\$ deux points distincts

$-\$ un point et une droite

$-\$ l'intersection de deux plans

$-\$ un système paramétrique

Exemple

Soient

$A\begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}$ et

$B\begin{pmatrix} -4\\ 1\\ 5 \end{pmatrix}$ deux points de l'espace

Déterminons les équations paramétriques et cartésiennes de

$(AB)$ .

On a : $\overrightarrow{AB}\begin{pmatrix}-5\\ -1\\2\end{pmatrix}$ . Soit $M\begin{pmatrix}x\\y\\z\end{pmatrix}\in (AB)$ alors, $\overrightarrow{AM}$ colinéaire à $\overrightarrow{AB}$ .

Donc, il existe

$k\in\mathbb{R}^{*}$ tel que

$\overrightarrow{AM}=k\overrightarrow{AB}$

$\Rightarrow \: \left\lbrace\begin{array} {lcl} x-1 &=& -5k\\ y-2 &=& -k\\ z-3 &=& 2k \end{array} \right. \text{ Ainsi, } \left\lbrace\begin{array} {lcl} x &=& -5k+1\\ y &=& -k+2\\ z &=& 2k+3 \end{array}\right.$ est l'équation paramétrique de

$(AB)$ .

Pour

$k=2-y$ nous obtenons :

$\left\lbrace\begin{array}{lcl} x-5y+9 &=& 0\\ 2y+z-7 &=& 0 \end{array}\right.$ qui constitue une équation cartésienne de

$(AB)$ .

$\centerdot\ \$ Un plan

$(\mathcal{P})$ de l'espace peut être défini et déterminé par :

$-\$ trois points non alignés
$-\$ un point $A$ et une droite qui lui est perpendiculaire ou un plan qui lui est parallèle.
$-\$ deux droites strictement parallèles ou sécantes
$-\$ une droite et un point extérieur à cette droite
$-\$ une équation cartésienne du type $ax+by+cz+d=0$ avec $a$ , $b$ et $c$ non tous nuls
$-\$ une représentation paramétrique

Exemple

Soient

$A\begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}$ ,

$\ B\begin{pmatrix} -1\\ 2\\ 5 \end{pmatrix}$ et

$C\begin{pmatrix} 2\\ 3\\ 4 \end{pmatrix}$ trois points de l'espace.

On a :

$M\begin{pmatrix} x\\ y\\ z \end{pmatrix}\in$ au plan

$(ABC)$ si, et seulement si, il existe

$k$ et

$k'$

$\in\mathbf{R}^{*}$ tels que

$\overrightarrow{AM}=k\overrightarrow{AB}+k'\overrightarrow{AC}$

Ainsi, une équation paramétrique du plan

$(ABC)$ est donnée par :

$\left\lbrace\begin{array}{lcl} x &=& -2k+k'+1\\ y &=& k'+2\\ z &=& 2k+k'+3 \end{array} \right.$

Et enfin, on déduit une équation cartésienne de la forme

$x-2y+z=0.$

Remarques

Soit un plan

$(\mathcal{P})$ d'équation :

$ax+by+cz+d=0$ alors

$\vec{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$ est un vecteur normal à

$(\mathcal{P}).$

II Positions relatives de droites et de plans

$\centerdot\ \$ Deux droites

$\Delta$ et

$\Delta'$ de l'espace sont soit coplanaires soit non coplanaires

$\centerdot\ \$ Une droite $\Delta$ et un plan de l'espace sont :

$-\$ soit sécants en un point $A$ , et on dit que la droite perce le plan
$-\$ soit la droite est parallèle au plan ( $\Delta\cap\mathcal{P}=\emptyset$ ou $\Delta\subset\mathcal{P}$ )

$\centerdot\ \$ Deux plans $\mathcal{P}$ et $\mathcal{P}'$ de l'espace sont soit parallèles $\mathcal{P}=\mathcal{P}'$ ou $\mathcal{P}\cap\mathcal{P}'=\emptyset$ , soit sécants $\mathcal{P}\cap\mathcal{P}'=\Delta$

III Parallélisme et orthogonalité dans l'espace

$\centerdot\ \$ Deux droites

$\Delta$ et

$\Delta'$ de l'espace sont parallèles si elles sont coplanaires et parallèles dans le plan

$\centerdot\ \$ Une droite $\Delta$ et un plan $\mathcal{P}$ sont parallèles si ( $\Delta\cap\mathcal{P}=\emptyset$ ou $\Delta\subset\mathcal{P}$ )

$\centerdot\ \$ Deux plans $\mathcal{P}$ et $\mathcal{P}'$ sont parallèles si $\mathcal{P}=\mathcal{P}'$ ou $\mathcal{P}\cap\mathcal{P}'=\emptyset$ . Les vecteurs normaux $\vec{n}$ et $\vec{n}'$ sont colinéaires

$\centerdot\ \$ Deux droites $\Delta$ et $\Delta'$ sont perpendiculaires

$-\$ si l'une parallèle à un plan perpendiculaire à l'autre
$-\$ et si en un point quelconque de l'espace elles sont perpendiculaires.

$\centerdot\ \$ Une droite $\Delta$ et un plan $\mathcal{P}$ sont perpendiculaires

$-\$ si $\Delta$ est perpendiculaire à deux droites sécantes de $\mathcal{P}$
$-\$ si $\Delta$ est perpendiculaire à toute droite $D\subset\mathcal{P}$
$-\$ si le vecteur directeur de $\Delta$ et $\vec{n}$ sont colinéaires.

$\centerdot\ \$ Deux plans $\mathcal{P}$ et $\mathcal{P}'$ sont perpendiculaires

$-\$ si l'un des plans contient une droite perpendiculaire à l'autre plan
$-\$ si $\vec{n}$ orthogonal à $\vec{n}'$

IV Produit vectoriel

IV.1 Orientations dans l'espace

On dira qu'un repère

$(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ est direct si, pour un observateur couché sur

$(Oz)$ , les point en

$O$ et fixant le point

$I$ , il a le point

$J$ à gauche. Dans le cas contraire le repère est dit indirect.

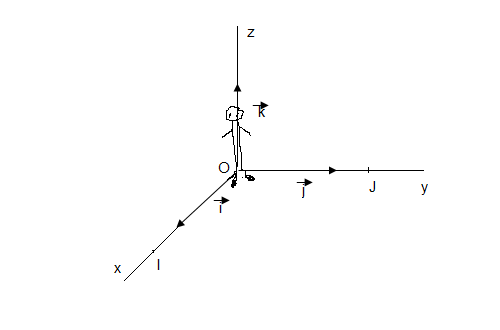
IV.2 Définitions

Soient

$\vec{u}$ et

$\vec{v}$ deux vecteurs. On appelle produit vectoriel des vecteurs

$\vec{u}$ et

$\vec{v}$ , le vecteur noté

$\vec{u}\wedge\vec{v}$ qui est :

$-\$ égal au vecteur nul si

$\vec{u}$ et

$\vec{v}$ sont colinéaires

$-\$ perpendiculaire à

$\vec{u}$ , à

$\vec{v}$ et

$(\vec{u}\;,\ \vec{v}\;,\ \vec{u}\wedge\vec{v})$ est direct et

$||\vec{u}\wedge\vec{v}||=||\vec{u}||\times||\vec{v}||\times|\sin(\vec{u}\;,\ \vec{v})|$

IV.3 Propriétés

$\centerdot\ \ \vec{u}\wedge\vec{v}=\vec{0}$ si, et seulement si,

$\vec{u}$ et

$\vec{v}$ sont colinéaires.

$\centerdot\ \ \vec{u}\wedge\vec{v}=-\vec{v}\wedge\vec{u}=$ (antisymétrique)

$\centerdot\ \ \alpha\in\mathbb{R}\;,\ (\alpha\vec{u}\wedge\vec{v})=(\vec{u}\wedge\alpha\vec{v})=\alpha(\vec{u}\wedge\vec{v})$

$\centerdot\ \ \vec{u}\wedge(\vec{v}+\vec{w})=\vec{u}\wedge\vec{v}+\vec{u}\wedge\vec{w}$

$\centerdot\ \ \alpha\vec{u}\wedge\rho\vec{v}=\alpha\rho(\vec{u}\wedge\vec{v})$

IV.4 Expression dans une base orthonormée

Soient

$\vec{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et

$\vec{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$ deux vecteurs de l'espace.

$\vec{i}$ ,

$\ \vec{j}$ et

$\vec{k}$ vecteurs unitaires du repère direct tels que

$\vec{i}\wedge\vec{j}=\vec{k}\;,\quad\vec{j}\wedge\vec{k}=\vec{i}\quad\text{et}\quad\vec{k}\wedge\vec{i}=\vec{j}$

Soient $\vec{u}=x\vec{i}+y\vec{j}+z\vec{k}$ et $\vec{u}=x'\vec{i}+y'\vec{j}+z'\vec{k}$

On a : $\begin{eqnarray}\vec{u}\wedge\vec{v}&=&(x\vec{i}+y\vec{j}+z\vec{k})\wedge(x'\vec{i}+y'\vec{j}+z'\vec{k})\nonumber\\ \\ \\&=&xy'\vec{k}-xz'\vec{j}-yx\vec{k}+yz'\vec{i}+zx'\vec{j}-zy'\vec{i} \nonumber\\ \\ \\&=&(yz'-zy')\vec{i}-(xz'-zx')\vec{j}+(xy'-yx')\vec{k} \nonumber\\ \\ \\&=&\vec{i}\begin{vmatrix} y&y'\\ z&z'\end{vmatrix}-\vec{j}\begin{vmatrix} x&x'\\ z&z'\end{vmatrix}+\vec{k}\begin{vmatrix} x&x'\\ y&y'\end{vmatrix} \nonumber \end{eqnarray}$

Donc,

$\vec{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}\wedge\vec{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}=\vec{i}\begin{vmatrix} y&y'\\ z&z' \end{vmatrix}-\vec{j}\begin{vmatrix} x&x'\\ z&z' \end{vmatrix}+\vec{k}\begin{vmatrix} x&x'\\ y&y' \end{vmatrix}$

IV.5 Applications

IV.5.1 Aire d'un triangle - aire d'un parallélogramme

Considérons le parallélogramme

$ABCD$ ci-dessous.

L'aire du triangle

$ABD$ , notée

$\mathcal{A}_{ABD}$ , est donnée par :

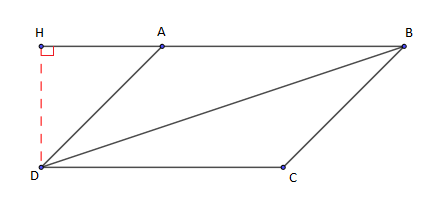
$\mathcal{A}_{ABD}=\dfrac{AB\times AH}{2}$ avec $H$ le projeté orthogonal de $D$ sur $(AB)$ .

On a : $\begin{eqnarray} AH&=&AD\times|\sin(\pi-(\overrightarrow{AB}\;,\ \overrightarrow{AD}))| \nonumber\\ \\ &=&AD\times|\sin(\overrightarrow{AB}\;,\ \overrightarrow{AD})| \nonumber \end{eqnarray}$

Donc,

$\begin{eqnarray}\mathcal{A}_{ABD}&=&\dfrac{AB\times AD\times|\sin(\overrightarrow{AB}\;,\ \overrightarrow{AD})|}{2} \nonumber\\ \\ &=&\dfrac{1}{2}||\overrightarrow{AB}\wedge\overrightarrow{AD}|| \nonumber \end{eqnarray}$

Et par suite, l'aire du parallélogramme

$ABCD$ notée

$\mathcal{A}_{ABCD}$ , est donnée par :

$\mathcal{A}_{ABCD}=||\overrightarrow{AB}\wedge\overrightarrow{AD}||$

IV.5.2 Distance d'un point à un plan

Soient

$\mathcal{P}$ un plan d'équation :

$ax+by+cz+d=0$ et

$M_{0}\begin{pmatrix} x_{0}\\ y_{0}\\ z_{0} \end{pmatrix}\notin\mathcal{P}$ .

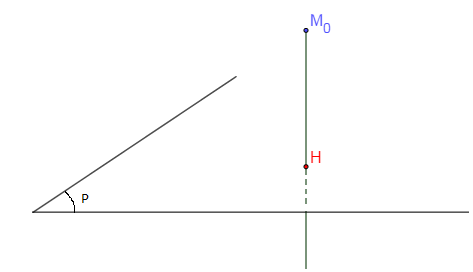
Soit $H$ le projeté orthogonal de $M_{0}$ sur le plan $\mathcal{P}$ . On note par $d(M_{0},\ \mathcal{P})$ la distance entre le point $M_{0}$ et le plan $\mathcal{P}$ .

On a : $d(M_{0}\;,\ \mathcal{P})=M_{0}H$ or $\overrightarrow{M_{0}H}$ est colinéaire à $\vec{n}\begin{pmatrix} a \\ b \\ c \end{pmatrix}$ , vecteur normal à $\mathcal{P}.$

Donc,

$|\overrightarrow{M_{0}H}\cdot\vec{n}|=||\overrightarrow{M_{0}H}||\cdot||\vec{n}||\ \Rightarrow\ M_{0}H=\dfrac{|\overrightarrow{M_{0}H}\cdot\vec{n}|}{||\vec{n}||}$

On a :

$\overrightarrow{M_{0}H}\begin{pmatrix} x_{H}-x_{0} \\ y_{H}-y_{0} \\ z_{H}-z_{0} \end{pmatrix}$ alors,

$\begin{eqnarray}\overrightarrow{M_{0}H}\cdot\vec{n}&=&a(x_{H}-x_{0})+b(y_{H}-y_{0})+c(z_{H}-z_{0}) \nonumber\\ \\ &=&\underbrace{ax_{H}+by_{H}+cz_{H}}_{0}-(ax_{0}+by_{0}+cz_{0})\ \text{ car }H\in\mathcal{P}\nonumber\\ \\ \Rightarrow\ \overrightarrow{M_{0}H}\cdot\vec{n}&=&-(ax_{0}+by_{0}+cz_{0}+d)\nonumber \end{eqnarray}$

D'où,

$M_{0}H=\dfrac{|ax_{0}+by_{0}+cz_{0}+d|}{\sqrt{a^{2}+b^{2}+c^{2}}}$

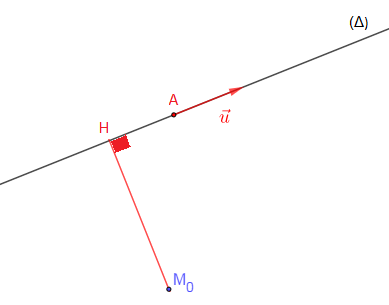
IV.5.3 Distance d'un point à une droite

Soit

$\Delta$ une droite, de vecteur directeur

$\vec{u}$ , passant par

$A$ . Soit

$M_{0}\notin\Delta$ de projeté orthogonal

$H$ sur

$\Delta$

Notons

$d(M_{0}\;,\ \Delta)$ la distance entre

$M_{0}$ et la droite

$\Delta.$

On a :

$\overrightarrow{M_{0}A}\wedge\vec{u}=\overrightarrow{M_{0}H}\wedge\vec{u}\$ et

$\ ||\overrightarrow{M_{0}H}\wedge\vec{u}||=M_{0}H\times||\vec{u}||$

Donc,

$d(M_{0}\;,\ \Delta)=M_{0}H=\dfrac{||\overrightarrow{M_{0}A}\wedge\vec{u}||}{||\vec{u}||}$

En effet,

on a ;

$\begin{eqnarray}\overrightarrow{M_{0}A}\wedge\vec{u}&=&(\overrightarrow{M_{0}H}+\overrightarrow{HA})\wedge\vec{u}\nonumber\\ \\ &=&\overrightarrow{M_{0}H}\wedge\vec{u}+\underbrace{\overrightarrow{HA}\wedge\vec{u}}_{\vec{0}}\;,\quad\text{car }\overrightarrow{HA}\text{ colinéaire à }\vec{u}\nonumber\\ \\ &=&\overrightarrow{M_{0}H}\wedge\vec{u}\nonumber\\ \\ \Rightarrow\ ||\overrightarrow{M_{0}A}\wedge\vec{u}||&=&||\overrightarrow{M_{0}H}\wedge\vec{u}||\ =\ ||\overrightarrow{ M_{0}H}||\times||\vec{u}||\times\sin\dfrac{\pi}{2}\nonumber \\ \\&=&M_{0}H\times||\vec{u}||\nonumber\\ \\ \Rightarrow\ M_{0}H&=&\dfrac{||\overrightarrow{M_{0}A}\wedge\vec{u}||}{||\vec{u}||}\nonumber \end{eqnarray}$

V Produit mixte

V.1 Définitions

Soient

$\vec{u}$ ,

$\ \vec{v}$ et

$\vec{w}$ trois vecteurs. On appelle produit mixte des vecteurs

$\vec{u}$ ,

$\ \vec{v}$ et

$\vec{w}$ le réel noté

$\vec{u}\cdot(\vec{v}\wedge\vec{w})$

V.2 Expression dans une base orthonormée

On se donne

$\vec{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ ,

$\ \vec{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}\$ et

$\ \vec{w}\begin{pmatrix} x''\\ y''\\ z'' \end{pmatrix}$ dans

$(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ , repère orthonormé.

On a :

$\vec{v}\wedge\vec{w}\begin{pmatrix} y'z''-y''z'\\ x''z'-x'z''\\ x'y''-y'x'' \end{pmatrix}$ .

Ainsi,

$\vec{u}\cdot(\vec{v}\wedge\vec{w})=x(y'z''-y''z')-y(x'z''-x''z')+z(x'y''-y'x'')$

D'où,

$\begin{eqnarray}\vec{u}\cdot(\vec{v}\wedge\vec{w})&=&\begin{vmatrix} x&x'&x''\\ y&y'&y''\\ z&z'&z'' \end{vmatrix} \nonumber \\ \\&=&x\begin{vmatrix} y'&y''\\ z'&z'' \end{vmatrix}-y\begin{vmatrix} x'&x''\\ z'&z'' \end{vmatrix}+z\begin{vmatrix} x'&x''\\ y'&y'' \end{vmatrix} \nonumber \end{eqnarray}$

En application, on peut constater que le volume

$\mathcal{V}_{ABCD}$ d'un tétraèdre

$ABCD$ est donné par :

$\mathcal{V}_{ABCD}=\dfrac{1}{6}\left|\overrightarrow{AD}\cdot(\overrightarrow{AB}\wedge\overrightarrow{AC})\right|$

Auteur:

Seyni Ndiaye & Diny Faye

Commentaires

Dįãllõ (non vérifié)

dim, 05/21/2023 - 03:40

Permalien

Oumar

Terminale

Email:

Oumarbelladiallo187@icloud.com

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Géométrie dans l'espace - T S1

Formulaire de recherche

I Détermination de droites et de plans

Exemple

Exemple

Remarques

II Positions relatives de droites et de plans

III Parallélisme et orthogonalité dans l'espace

IV Produit vectoriel

IV.1 Orientations dans l'espace

IV.2 Définitions

IV.3 Propriétés

IV.4 Expression dans une base orthonormée

IV.5 Applications

IV.5.1 Aire d'un triangle - aire d'un parallélogramme

IV.5.2 Distance d'un point à un plan

IV.5.3 Distance d'un point à une droite

V Produit mixte

V.1 Définitions

V.2 Expression dans une base orthonormée

Commentaires

Oumar

Ajouter un commentaire

Plain text