Géométrie dans l'espace - T S1

I Détermination de droites et de plans

$\centerdot\ \ $ Une droite $\Delta$ de l'espace est entièrement déterminée par :
 
$-\ $ deux points distincts
$-\ $ un point et une droite
$-\ $ l'intersection de deux plans
$-\ $ un système paramétrique

Exemple

Soient $A\begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}$ et $B\begin{pmatrix} -4\\ 1\\ 5 \end{pmatrix}$ deux points de l'espace
 
Déterminons les équations paramétriques et cartésiennes de $(AB)$.

On a : $\overrightarrow{AB}\begin{pmatrix}-5\\ -1\\2\end{pmatrix}$. Soit $M\begin{pmatrix}x\\y\\z\end{pmatrix}\in (AB)$ alors, $\overrightarrow{AM}$ colinéaire à $\overrightarrow{AB}$.
 

Donc, il existe $k\in\mathbb{R}^{*}$ tel que $\overrightarrow{AM}=k\overrightarrow{AB}$
 
$\Rightarrow \: \left\lbrace\begin{array} {lcl}
  x-1 &=& -5k\\
y-2 &=& -k\\
z-3 &=& 2k
 \end{array} \right. \text{ Ainsi, } \left\lbrace\begin{array} {lcl}
  x &=& -5k+1\\
y &=& -k+2\\
z &=& 2k+3
 \end{array}\right.$ est l'équation paramétrique de $(AB)$.
 
Pour $k=2-y$ nous obtenons : $\left\lbrace\begin{array}{lcl}
x-5y+9 &=& 0\\
2y+z-7 &=& 0
\end{array}\right.$qui constitue une équation cartésienne de $(AB)$.
 
$\centerdot\ \ $ Un plan $(\mathcal{P})$ de l'espace peut être défini et déterminé par :

$-\ $ trois points non alignés
$-\ $ un point $A$ et une droite qui lui est perpendiculaire ou un plan qui lui est parallèle.
$-\ $ deux droites strictement parallèles ou sécantes
$-\ $ une droite et un point extérieur à cette droite
$-\ $ une équation cartésienne du type $ax+by+cz+d=0$ avec $a$, $b$ et $c$ non tous nuls
$-\ $ une représentation paramétrique

Exemple

Soient $A\begin{pmatrix}
1\\
2\\
3
\end{pmatrix}$,  $\ B\begin{pmatrix}
-1\\
2\\
5
\end{pmatrix}$ et  $C\begin{pmatrix}
2\\
3\\
4
\end{pmatrix}$ trois points de l'espace.
 
On a  : $M\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}\in$ au plan $(ABC)$ si, et seulement si, il existe $k$ et $k'$ $\in\mathbf{R}^{*}$ tels que $$\overrightarrow{AM}=k\overrightarrow{AB}+k'\overrightarrow{AC}$$
 
Ainsi, une équation paramétrique du plan $(ABC)$ est donnée par :
 
$\left\lbrace\begin{array}{lcl}
x &=& -2k+k'+1\\
y &=& k'+2\\
z &=& 2k+k'+3
\end{array}
\right.$
 
Et enfin, on déduit une équation cartésienne de la forme $x-2y+z=0.$

Remarques

Soit un plan $(\mathcal{P})$ d'équation : $ax+by+cz+d=0$ alors $\vec{n}\begin{pmatrix}
a\\
b\\
c
\end{pmatrix}$ est un vecteur normal à $(\mathcal{P}).$

II Positions relatives de droites et de plans

$\centerdot\ \ $ Deux droites $\Delta$ et $\Delta'$ de l'espace sont soit coplanaires soit non coplanaires

$\centerdot\ \ $ Une droite $\Delta$ et un plan de l'espace sont :

$-\ $ soit sécants en un point $A$, et on dit que la droite perce le plan
$-\ $ soit la droite est parallèle au plan ($\Delta\cap\mathcal{P}=\emptyset$ ou $\Delta\subset\mathcal{P}$)

$\centerdot\ \ $ Deux plans $\mathcal{P}$ et $\mathcal{P}'$ de l'espace sont soit parallèles $\mathcal{P}=\mathcal{P}'$ ou $\mathcal{P}\cap\mathcal{P}'=\emptyset$, soit sécants  $\mathcal{P}\cap\mathcal{P}'=\Delta$

III Parallélisme et orthogonalité dans l'espace

$\centerdot\ \ $ Deux droites $\Delta$ et $\Delta'$ de l'espace sont parallèles si elles sont coplanaires et parallèles dans le plan

$\centerdot\ \ $ Une droite $\Delta$ et un plan $\mathcal{P}$ sont parallèles si ($\Delta\cap\mathcal{P}=\emptyset$ ou $\Delta\subset\mathcal{P}$)

$\centerdot\ \ $ Deux plans $\mathcal{P}$ et $\mathcal{P}'$ sont parallèles si $\mathcal{P}=\mathcal{P}'$ ou $\mathcal{P}\cap\mathcal{P}'=\emptyset$. Les vecteurs normaux $\vec{n}$ et $\vec{n}'$ sont colinéaires

$\centerdot\ \ $ Deux droites $\Delta$ et $\Delta'$ sont perpendiculaires

$-\ $ si l'une parallèle à un plan perpendiculaire à l'autre
$-\ $ et si en un point quelconque de l'espace elles sont perpendiculaires.

$\centerdot\ \ $ Une droite $\Delta$ et un plan $\mathcal{P}$ sont perpendiculaires

$-\ $ si $\Delta$ est perpendiculaire à deux droites sécantes de $\mathcal{P}$
$-\ $ si $\Delta$ est perpendiculaire à toute droite $D\subset\mathcal{P}$
$-\ $ si le vecteur directeur de $\Delta$ et $\vec{n}$ sont colinéaires.

$\centerdot\ \ $ Deux plans $\mathcal{P}$ et $\mathcal{P}'$ sont perpendiculaires

$-\ $ si l'un des plans contient une droite perpendiculaire à l'autre plan
$-\ $ si $\vec{n}$ orthogonal à $\vec{n}'$

IV Produit vectoriel

IV.1 Orientations dans l'espace

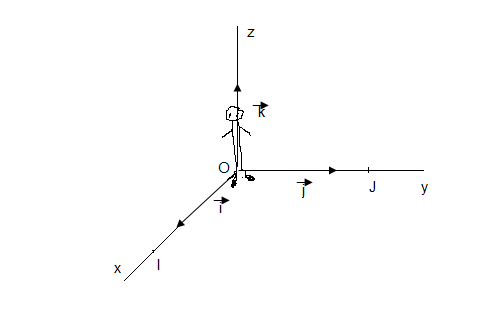
On dira qu'un repère $(O\;,\  \vec{i}\;,\  \vec{j}\;,\  \vec{k})$ est direct si, pour un observateur couché sur $(Oz)$, les point en $O$ et fixant le point $I$, il a le point $J$ à gauche. Dans le cas contraire le repère est dit indirect.
 

IV.2 Définitions

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs. On appelle produit vectoriel des vecteurs $\vec{u}$ et $\vec{v}$, le vecteur noté $\vec{u}\wedge\vec{v}$ qui est :

$-\ $ égal au vecteur nul si $\vec{u}$ et $\vec{v}$ sont colinéaires 
$-\ $ perpendiculaire à $\vec{u}$, à $\vec{v}$ et $(\vec{u}\;,\ \vec{v}\;,\ \vec{u}\wedge\vec{v})$ est direct et 
$$||\vec{u}\wedge\vec{v}||=||\vec{u}||\times||\vec{v}||\times|\sin(\vec{u}\;,\ \vec{v})|$$

IV.3 Propriétés

$\centerdot\ \ \vec{u}\wedge\vec{v}=\vec{0}$ si, et seulement si, $\vec{u}$ et $\vec{v}$ sont colinéaires.
 
$\centerdot\ \ \vec{u}\wedge\vec{v}=-\vec{v}\wedge\vec{u}=$ (antisymétrique)
 
$\centerdot\ \ \alpha\in\mathbb{R}\;,\ (\alpha\vec{u}\wedge\vec{v})=(\vec{u}\wedge\alpha\vec{v})=\alpha(\vec{u}\wedge\vec{v})$
 
$\centerdot\ \ \vec{u}\wedge(\vec{v}+\vec{w})=\vec{u}\wedge\vec{v}+\vec{u}\wedge\vec{w}$
 
$\centerdot\ \ \alpha\vec{u}\wedge\rho\vec{v}=\alpha\rho(\vec{u}\wedge\vec{v})$

IV.4 Expression dans une base orthonormée

Soient $\vec{u}\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}$ et $\vec{v}\begin{pmatrix}
x'\\
y'\\
z'
\end{pmatrix}$ deux vecteurs de l'espace. $\vec{i}$, $\ \vec{j}$ et $\vec{k}$ vecteurs unitaires du repère direct tels que $$\vec{i}\wedge\vec{j}=\vec{k}\;,\quad\vec{j}\wedge\vec{k}=\vec{i}\quad\text{et}\quad\vec{k}\wedge\vec{i}=\vec{j}$$

Soient $\vec{u}=x\vec{i}+y\vec{j}+z\vec{k}$ et $\vec{u}=x'\vec{i}+y'\vec{j}+z'\vec{k}$

On a : \begin{eqnarray}\vec{u}\wedge\vec{v}&=&(x\vec{i}+y\vec{j}+z\vec{k})\wedge(x'\vec{i}+y'\vec{j}+z'\vec{k})\nonumber\\ \\ \\&=&xy'\vec{k}-xz'\vec{j}-yx\vec{k}+yz'\vec{i}+zx'\vec{j}-zy'\vec{i} \nonumber\\ \\ \\&=&(yz'-zy')\vec{i}-(xz'-zx')\vec{j}+(xy'-yx')\vec{k} \nonumber\\ \\ \\&=&\vec{i}\begin{vmatrix} y&y'\\ z&z'\end{vmatrix}-\vec{j}\begin{vmatrix} x&x'\\ z&z'\end{vmatrix}+\vec{k}\begin{vmatrix} x&x'\\ y&y'\end{vmatrix} \nonumber \end{eqnarray}

 
Donc, $\vec{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}\wedge\vec{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}=\vec{i}\begin{vmatrix} y&y'\\ z&z' \end{vmatrix}-\vec{j}\begin{vmatrix} x&x'\\ z&z' \end{vmatrix}+\vec{k}\begin{vmatrix} x&x'\\ y&y' \end{vmatrix}$

IV.5 Applications

IV.5.1 Aire d'un triangle - aire d'un parallélogramme

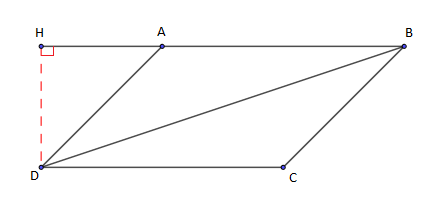
Considérons le parallélogramme $ABCD$ ci-dessous.
 

 
 
L'aire du triangle $ABD$, notée $\mathcal{A}_{ABD}$, est donnée par :

$\mathcal{A}_{ABD}=\dfrac{AB\times AH}{2}$ avec $H$ le projeté orthogonal de $D$ sur $(AB)$.

On a : \begin{eqnarray} AH&=&AD\times|\sin(\pi-(\overrightarrow{AB}\;,\ \overrightarrow{AD}))| \nonumber\\ \\ &=&AD\times|\sin(\overrightarrow{AB}\;,\ \overrightarrow{AD})| \nonumber \end{eqnarray}

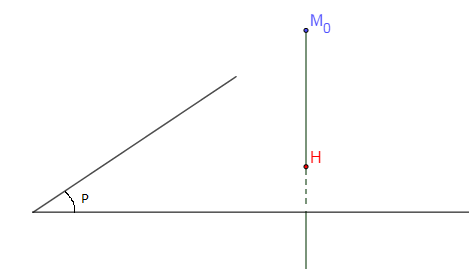
Donc, \begin{eqnarray}\mathcal{A}_{ABD}&=&\dfrac{AB\times AD\times|\sin(\overrightarrow{AB}\;,\ \overrightarrow{AD})|}{2} \nonumber\\ \\ &=&\dfrac{1}{2}||\overrightarrow{AB}\wedge\overrightarrow{AD}|| \nonumber \end{eqnarray}
Et par suite, l'aire du parallélogramme $ABCD$ notée $\mathcal{A}_{ABCD}$, est donnée par : $$\mathcal{A}_{ABCD}=||\overrightarrow{AB}\wedge\overrightarrow{AD}||$$

IV.5.2 Distance d'un point à un plan

Soient $\mathcal{P}$ un plan d'équation : $ax+by+cz+d=0$ et $M_{0}\begin{pmatrix}
x_{0}\\
y_{0}\\
z_{0}
\end{pmatrix}\notin\mathcal{P}$.

Soit $H$ le projeté orthogonal de $M_{0}$ sur le plan $\mathcal{P}$. On note par $d(M_{0},\ \mathcal{P})$ la distance entre le point $M_{0}$ et le plan $\mathcal{P}$.

On a :  $d(M_{0}\;,\ \mathcal{P})=M_{0}H$ or $\overrightarrow{M_{0}H}$ est colinéaire à $\vec{n}\begin{pmatrix} a \\ b \\ c \end{pmatrix}$, vecteur normal à $\mathcal{P}.$

 
Donc, $|\overrightarrow{M_{0}H}\cdot\vec{n}|=||\overrightarrow{M_{0}H}||\cdot||\vec{n}||\ \Rightarrow\ M_{0}H=\dfrac{|\overrightarrow{M_{0}H}\cdot\vec{n}|}{||\vec{n}||}$
 
On a : $\overrightarrow{M_{0}H}\begin{pmatrix} x_{H}-x_{0} \\ y_{H}-y_{0} \\ z_{H}-z_{0} \end{pmatrix}$ alors, 
\begin{eqnarray}\overrightarrow{M_{0}H}\cdot\vec{n}&=&a(x_{H}-x_{0})+b(y_{H}-y_{0})+c(z_{H}-z_{0}) \nonumber\\ \\ &=&\underbrace{ax_{H}+by_{H}+cz_{H}}_{0}-(ax_{0}+by_{0}+cz_{0})\ \text{ car }H\in\mathcal{P}\nonumber\\ \\ \Rightarrow\ \overrightarrow{M_{0}H}\cdot\vec{n}&=&-(ax_{0}+by_{0}+cz_{0}+d)\nonumber \end{eqnarray}
D'où, $$M_{0}H=\dfrac{|ax_{0}+by_{0}+cz_{0}+d|}{\sqrt{a^{2}+b^{2}+c^{2}}}$$
 

 

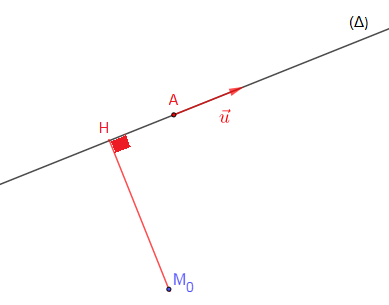
 IV.5.3 Distance d'un point à une droite

Soit $\Delta$ une droite, de vecteur directeur $\vec{u}$, passant par $A$. Soit $M_{0}\notin\Delta$ de projeté orthogonal $H$ sur $\Delta$

Notons $d(M_{0}\;,\ \Delta)$ la distance entre $M_{0}$ et la droite $\Delta.$
 
On a : $\overrightarrow{M_{0}A}\wedge\vec{u}=\overrightarrow{M_{0}H}\wedge\vec{u}\ $ et $\ ||\overrightarrow{M_{0}H}\wedge\vec{u}||=M_{0}H\times||\vec{u}||$
 
Donc, $$d(M_{0}\;,\ \Delta)=M_{0}H=\dfrac{||\overrightarrow{M_{0}A}\wedge\vec{u}||}{||\vec{u}||}$$
 
En effet, 
 
on a ;
\begin{eqnarray}\overrightarrow{M_{0}A}\wedge\vec{u}&=&(\overrightarrow{M_{0}H}+\overrightarrow{HA})\wedge\vec{u}\nonumber\\ \\ &=&\overrightarrow{M_{0}H}\wedge\vec{u}+\underbrace{\overrightarrow{HA}\wedge\vec{u}}_{\vec{0}}\;,\quad\text{car }\overrightarrow{HA}\text{ colinéaire à }\vec{u}\nonumber\\ \\ &=&\overrightarrow{M_{0}H}\wedge\vec{u}\nonumber\\ \\ \Rightarrow\ ||\overrightarrow{M_{0}A}\wedge\vec{u}||&=&||\overrightarrow{M_{0}H}\wedge\vec{u}||\ =\ ||\overrightarrow{ M_{0}H}||\times||\vec{u}||\times\sin\dfrac{\pi}{2}\nonumber \\ \\&=&M_{0}H\times||\vec{u}||\nonumber\\ \\ \Rightarrow\ M_{0}H&=&\dfrac{||\overrightarrow{M_{0}A}\wedge\vec{u}||}{||\vec{u}||}\nonumber \end{eqnarray}

 

 

V Produit mixte

 V.1 Définitions

Soient $\vec{u}$, $\ \vec{v}$ et $\vec{w}$ trois vecteurs. On appelle produit mixte des vecteurs $\vec{u}$, $\ \vec{v}$ et $\vec{w}$ le réel noté $\vec{u}\cdot(\vec{v}\wedge\vec{w})$

V.2 Expression dans une base orthonormée

On se donne $\vec{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ , $\ \vec{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}\ $ et $\ \vec{w}\begin{pmatrix} x''\\ y''\\ z'' \end{pmatrix}$ dans $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$, repère orthonormé.
 
On a : $\vec{v}\wedge\vec{w}\begin{pmatrix} y'z''-y''z'\\ x''z'-x'z''\\ x'y''-y'x'' \end{pmatrix}$.
 
Ainsi, $\vec{u}\cdot(\vec{v}\wedge\vec{w})=x(y'z''-y''z')-y(x'z''-x''z')+z(x'y''-y'x'')$
 
D'où,  \begin{eqnarray}\vec{u}\cdot(\vec{v}\wedge\vec{w})&=&\begin{vmatrix} x&x'&x''\\ y&y'&y''\\ z&z'&z'' \end{vmatrix} \nonumber \\ \\&=&x\begin{vmatrix} y'&y''\\ z'&z'' \end{vmatrix}-y\begin{vmatrix} x'&x''\\ z'&z'' \end{vmatrix}+z\begin{vmatrix} x'&x''\\ y'&y'' \end{vmatrix} \nonumber \end{eqnarray}
 
En application, on peut constater que le volume $\mathcal{V}_{ABCD}$ d'un tétraèdre $ABCD$ est donné par :
$$\mathcal{V}_{ABCD}=\dfrac{1}{6}\left|\overrightarrow{AD}\cdot(\overrightarrow{AB}\wedge\overrightarrow{AC})\right|$$
 
Auteur: 
Seyni Ndiaye & Diny Faye

Commentaires

Dįãllõ (non vérifié)

dim, 05/21/2023 - 03:40

Terminale
Email: 
Oumarbelladiallo187@icloud.com

Ajouter un commentaire

Plus d'information sur les formats de texte

Plain text

  • Aucune balise HTML autorisée.
  • Les adresses de pages web et de courriels sont transformées en liens automatiquement.