Vous êtes ici

Solution des exercices : Notion de réaction chimique - 4e

Classe:

Quatrième

Exercice 1

Complétons le texte suivant en ajoutant les mots ou groupes de mots manquants.

a) La transformation de certains corps purs en d'autres corps purs est appelée réaction.

b) Les corps purs qui disparaissent sont les réactifs alors que ceux qui apparaissent sont les produits.

c) Au cours d'une réaction chimique il y a une transformation de la matière.

d) Une réaction est représentée par une équation bilan.

Exercice 2

Exercice 3

Dans cet exercice, il s'agit d'équilibrer des équations bilan de quelques réactions chimiques.

Pour cela, on utilise le principe de la conservation de la matière : au cours d'une réaction chimique, il y a une conservation de la matière.

Ainsi, pour chaque élément chimique, on doit avoir le même nombre d'atomes dans les réactifs que dans les produits.

Cela revient donc à mettre des coefficients appropriés devant les produits et les réactifs.

Ce qui donne enfin une équation bilan équilibrée.

Appliquons cette méthode pour équilibrer chacune des équations chimiques ci-dessous.

$NH_{3}+\dfrac{5}{4}O_{2}\ \longrightarrow\ NO+\dfrac{3}{2}H_{2}O$

$9C+2Al_{2}O_{3}\ \longrightarrow\ Al_{4}C_{3}+6CO$

$C_{2}H_{4}O+\dfrac{5}{2}O_{2}\ \longrightarrow\ 2CO_{2}+2H_{2}O$

$Fe_{3}O_{4}+4H_{2}\ \longrightarrow\ 3Fe+4H_{2}O$

$H_{2}S+Cl_{2}\ \longrightarrow\ 2HCl+S$

$Cl_{2}+2NaOH\ \longrightarrow\ NaCl+NaOCl+H_{2}O$

$CH_{4}+O_{2}\ \longrightarrow\ C+2H_{2}O$

Exercice 4

Pour avoir $56\;ml$ de dihydrogène dans les conditions normales, un laborantin fait agir l'acide chlorhydrique dilué sur du zinc.

1) Trouvons La masse de chacun des réactifs ; $HCl\ $ et $\ Zn$

$\centerdot\ \ $ Masse de $HCl$

Pour cela, on établit d'abord l'équation de la réaction entre l'acide chlorhydrique dilué et le zinc. On a : $$HCl+Zn\ \longrightarrow\ H_{2}+ZnCl_{2}$$

En équilibrant ensuite cette équation, on obtient l'équation bilan équilibrée qui vérifie la conservation de la matière : $$2HCl+Zn\ \longrightarrow\ H_{2}+ZnCl_{2}$$

Enfin, en observant cette équation bilan, nous constatons qu'au niveau macroscopique, 2 moles d'acide se combinent avec une mole de zinc pour donner une mole de dihydrogène et une mole de chlorure de zinc.

D'où, la correspondance suivante :

$$\begin{array}{rcl} 2\;moles_{_{HCl}}&\longrightarrow&1\;mole_{_{H_{2}}}\\n_{_{HCl}}&\longrightarrow&n_{_{H_{2}}}\end{array}$$

En utilisant les rapports de proportionnalité, on obtient : $$\dfrac{n_{_{HCl}}}{2}=\dfrac{n_{_{H_{2}}}}{1}$$

Ce qui donne : $$\boxed{n_{_{HCl}}=2\times n_{_{H_{2}}}}\qquad(\text{égalité 1})$$

Or, on sait que : $n_{_{HCl}}=\dfrac{m_{_{HCl}}}{M_{_{HCl}}}\ $ et $\ n_{_{H_{2}}}=\dfrac{V_{_{H_{2}}}}{V_{_{M}}}$

En remplaçant ces expressions de $n_{_{HCl}}\ $ et $\ n_{_{H_{2}}}$ dans l'égalité (1), on obtient : $$\dfrac{m_{_{HCl}}}{M_{_{HCl}}}=2\times\dfrac{V_{_{H_{2}}}}{V_{_{M}}}$$

Par suite, $$\boxed{m_{_{HCl}}=2\times\dfrac{V_{_{H_{2}}}\times M_{_{HCl}}}{V_{_{M}}}}$$

Avec : $V_{_{M}}=22.4\;l.mol^{-1}\;,\ V_{_{H_{2}}}=56\;ml=0.056\;l $ et

$\begin{array}{rcl} M_{_{HCl}}=M_{_{H}}+M_{_{Cl}}&=&1+35.5\\&=&36.5\;g.mol^{-1}\end{array}$

Application numérique : $m_{_{HCl}}=2\times\dfrac{0.056\times 36.5}{22.4}=0.182$

D'où, $$\boxed{m_{_{HCl}}=0.182\;g}$$

$\centerdot\ \ $ Masse de $Zn$

En procédant de la même manière, on obtient la correspondance suivante :

$$\begin{array}{rcl} 1\;mole_{_{Zn}}&\longrightarrow&1\;mole_{_{H_{2}}}\\n_{_{Zn}}&\longrightarrow&n_{_{H_{2}}}\end{array}$$

Ainsi, $$\dfrac{n_{_{Zn}}}{1}=\dfrac{n_{_{H_{2}}}}{1}$$

Par suite, $$\boxed{n_{_{Zn}}=n_{_{H_{2}}}}\qquad(\text{égalité 2})$$

Comme $n_{_{Zn}}=\dfrac{m_{_{Zn}}}{M_{_{Zn}}}\ $ et $\ n_{_{H_{2}}}=\dfrac{V_{_{H_{2}}}}{V_{_{M}}}$ alors, en remplaçant dans l'égalité (2), on obtient : $$\dfrac{m_{_{Zn}}}{M_{_{Zn}}}=\dfrac{V_{_{H_{2}}}}{V_{_{M}}}$$

Par conséquent, $$\boxed{m_{_{Zn}}=\dfrac{V_{_{H_{2}}}\times M_{_{Zn}}}{V_{_{M}}}}$$

Avec : $V_{_{M}}=22.4\;l.mol^{-1}\;,\ V_{_{H_{2}}}=56\;ml=0.056\;l $ et $\ M_{_{Zn}}=65\;g.mol^{-1}$

Application numérique : $m_{_{Zn}}=\dfrac{0.056\times 65}{22.4}=0.162$

D'où, $$\boxed{m_{_{Zn}}=0.162\;g}$$

2) Trouvons La masse de chlorure de zinc $ZnCl_{2}$ obtenu en même temps.

En partant toujours de l'équation bilan et en adoptant la même démarche que dans la question 1), on obtient la correspondance suivante :

$$\begin{array}{rcl} 1\;mole_{_{H_{2}}}&\longrightarrow&1\;mole_{_{ZnCl_{2}}}\\n_{_{H_{2}}}&\longrightarrow&n_{_{ZnCl_{2}}}\end{array}$$

Ce qui donne : $$\dfrac{n_{_{ZnCl_{2}}}}{1}=\dfrac{n_{_{H_{2}}}}{1}$$

D'où, $$\boxed{n_{_{ZnCl_{2}}}=n_{_{H_{2}}}}\qquad(\text{égalité 3})$$

Or, on sait que : $n_{_{ZnCl_{2}}}=\dfrac{m_{_{ZnCl_{2}}}}{M_{_{ZnCl_{2}}}}\ $ et $\ n_{_{H_{2}}}=\dfrac{V_{_{H_{2}}}}{V_{_{M}}}$

Donc, en remplaçant ces expressions de $n_{_{ZnCl_{2}}}\ $ et $\ n_{_{H_{2}}}$ dans l'égalité (3), on obtient : $$\dfrac{m_{_{ZnCl_{2}}}}{M_{_{ZnCl_{2}}}}=\dfrac{V_{_{H_{2}}}}{V_{_{M}}}$$

Par suite, $$\boxed{m_{_{ZnCl_{2}}}=\dfrac{V_{_{H_{2}}}\times M_{_{ZnCl_{2}}}}{V_{_{M}}}}$$

Avec : $V_{_{M}}=22.4\;l.mol^{-1}\;,\ V_{_{H_{2}}}=56\;ml=0.056\;l $ et

$\begin{array}{rcl} M_{_{ZnCl_{2}}}=M_{_{Zn}}+2M_{_{Cl}}&=&65+2\times 35.5\\&=&136\;g.mol^{-1}\end{array}$

Application numérique : $m_{_{ZnCl_{2}}}=\dfrac{0.056\times 136}{22.4}=0.34$

D'où, $$\boxed{m_{_{ZnCl_{2}}}=0.34\;g}$$

Exercice 5

On brûle un morceau de $1200\;mg$ de carbone de l'air.

1) Trouvons le volume de dioxyde de carbone $CO_{2}$ produit par la réaction, dans les conditions normales.

Pour cela, nous allons d'abord établir l'équation bilan de la réaction, donnée par : $$C+O_{2}\ \longrightarrow\ CO_{2}$$

Ensuite, partant de cette équation, nous obtenons les correspondances suivantes :

$$\begin{array}{rcl} 1\;moles_{_{C}}&\longrightarrow&1\;mole_{_{CO_{2}}}\\n_{_{C}}&\longrightarrow&n_{_{CO_{2}}}\end{array}$$

Enfin, en utilisant les rapports de proportionnalité, on obtient : $$\dfrac{n_{_{C}}}{1}=\dfrac{n_{_{CO_{2}}}}{1}$$

Ce qui donne :
$$\boxed{n_{_{C}}=n_{_{CO_{2}}}}\qquad(\text{égalité 1})$$

Or, on sait que : $n_{_{C}}=\dfrac{m_{_{C}}}{M_{_{C}}}\ $ et $\ n_{_{CO_{2}}}=\dfrac{V_{_{CO_{2}}}}{V_{_{M}}}$

En remplaçant ces expressions de $n_{_{C}}\ $ et $\ n_{_{CO_{2}}}$ dans l'égalité (1), on obtient :
$$\dfrac{m_{_{C}}}{M_{_{C}}}=\dfrac{V_{_{CO_{2}}}}{V_{_{M}}}$$

Par suite, $$\boxed{V_{_{CO_{2}}}=\dfrac{m_{_{C}}\times V_{_{M}}}{M_{_{C}}}}$$

où : $V_{_{M}}=22.4\;l.mol^{-1}\;,\ M_{_{C}}=12\;g.mol^{-1}\ $ et $\ m_{_{C}}=1200\;mg=1.2\;g$

Application numérique : $V_{_{CO_{2}}}=\dfrac{1.2\times 22.4}{12}=2.24$

D'où, $$\boxed{V_{_{CO_{2}}}=2.24\;l}$$

2) Trouvons le volume de dioxygène nécessaire à cette combustion, dans les conditions normales.

En considérant toujours l'équation bilan de la réaction, on obtient les correspondances suivantes :
$$\begin{array}{rcl} 1\;moles_{_{O_{2}}}&\longrightarrow&1\;mole_{_{CO_{2}}}\\n_{_{O_{2}}}&\longrightarrow&n_{_{CO_{2}}}\end{array}$$

Ce qui se traduit par : $$\boxed{n_{_{O_{2}}}=n_{_{CO_{2}}}}\qquad(\text{égalité 2})$$

Comme $n_{_{O_{2}}}=\dfrac{V_{_{O_{2}}}}{V_{_{M}}}\ $ et $\ n_{_{CO_{2}}}=\dfrac{V_{_{CO_{2}}}}{V_{_{M}}}$ alors, en remplaçant dans l'égalité (2), on trouve :
$$\dfrac{V_{_{O_{2}}}}{V_{_{M}}}=\dfrac{V_{_{CO_{2}}}}{V_{_{M}}}$$

Par suite, $$\boxed{V_{_{O_{2}}}=V_{_{CO_{2}}}}$$

Or, on avait trouvait à la question 1) $V_{_{CO_{2}}}=2.24\;l$

Par conséquent, $$\boxed{V_{_{O_{2}}}=2.24\;l}$$

En déduisons le volume d'air utilisé.

Nous constatons, qu'en volume, l'air contient $\dfrac{1}{5}$ de dioxygène ; ces-à-dire, le volume de dioxygène représente $\dfrac{1}{5}$ du volume d'air.

Ce qui se traduit alors par : $$V_{_{O_{2}}}=\dfrac{1}{5}V_{_{\text{air}}}$$

Par suite, $$\boxed{V_{_{\text{air}}}=5\times V_{_{O_{2}}}}$$

A.N : $V_{_{\text{air}}}=5\times 2.24=11.2$

Ainsi, $$\boxed{V_{_{\text{air}}}=11.2\;l}$$

Exercice 6 Maitrise de connaissance

Complétons les phrases suivantes par les mots ou expressions qui conviennent :

Il y a transformation chimique lorsque des espèces chimiques appelées réactifs disparaissent et que d'autres appelées produits apparaissent.

La transformation chimique limitée aux réactifs et aux produits s'appelle réaction chimique.

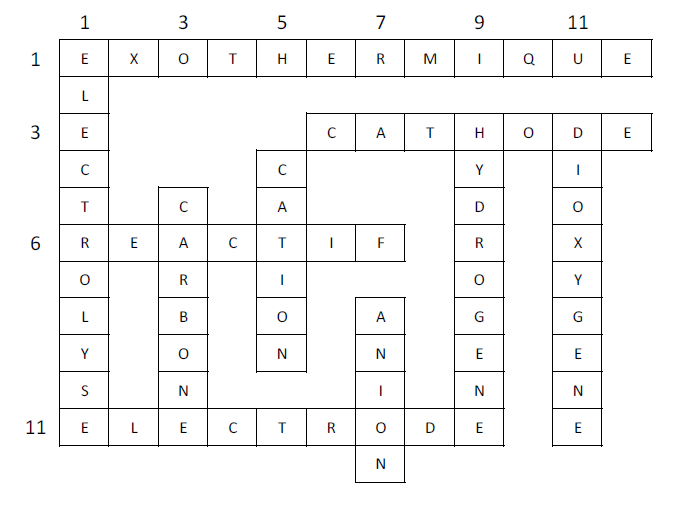
Lorsqu'une réaction chimique dégage de la chaleur, on dit qu'elle est exothermique.

Une équation bilan traduit de façon symbolique une réaction chimique.

Exercice 7 Équilibrage

Équilibrons les équations chimiques qui suivent :

Pour cela, nous procédons comme dans l'exercie 3, en utilisant le principe de la conservation de la matière.

Ainsi, pour chaque élément chimique, on doit avoir le même nombre d'atomes dans les réactifs que dans les produits.

Ce qui revient donc à mettre des coefficients appropriés devant les produits et les réactifs.

$\begin{array}{lrcl} 1)&2Na\ +\ \dfrac{1}{2}O_{2}&\longrightarrow&Na_{2}O\\ \\2)&CO\ +\ \dfrac{1}{2}O_{2}&\longrightarrow&CO_{2}\\ \\3)&H_{2}\ +\ \dfrac{1}{2}O_{2}&\longrightarrow&H_{2}O\\ \\4)&2CuO\ +\ C&\longrightarrow&2Cu\ +\ CO_{2}\\ \\5)&N_{2}O_{5}&\longrightarrow&2NO_{2}\ +\ \dfrac{1}{2}O_{2}\\ \\6)&C_{4}H_{10}\ +\ \dfrac{13}{2}O_{2}&\longrightarrow&4CO_{2}\ +\ 5H_{2}O\\ \\7)&6CO_{2}\ +\ 6H_{2}O&\longrightarrow&C_{6}H_{12}O_{6}\ +\ 6O_{2}\\ \\8)&C_{12}H_{22}O_{11}\ +\ 8O_{2}O&\longrightarrow&12CO_{2}\ +\ 11H_{2}O\\ \\9)&N_{2}\ +\ 3H_{2}&\longrightarrow&2NH_{3}\\ \\10)&2Fe\ +\ \dfrac{3}{2} O_{2}&\longrightarrow&Fe_{2}O_{3}\\ \\11)&Fe_{2}O_{3}\ +\ 3Al&\longrightarrow&2Fe\end{array}$

Exercice 8 Bilan molaire

A chaud, l'aluminium brûle dans le soufre.

L'équation-bilan qui traduit cette réaction s'écrit :

$$Al\ +\ S\ \rightarrow\ Al_{2}S_{3}$$

1) Déterminons la quantité minimale d'aluminium nécessaire pour faire réagir une mole de soufre.

En équilibrant l'équation de la réaction, on obtient l'équation bilan suivante :

$$2Al\ +\ 3S\ \rightarrow\ Al_{2}S_{3}$$

Par suite, cette équation bilan de la réaction permet d'établir les correspondances suivantes :

$$\begin{array}{rcl} 2\;moles_{_{(Al)}}&\longrightarrow&3\;moles_{_{(S)}}\\n_{_{Al}}&\longrightarrow&n_{_{S}}\end{array}$$

Ainsi, en appliquant les rapports de proportionnalité, on obtient :

$$\dfrac{n_{_{Al}}}{2}=\dfrac{n_{_{S}}}{3}\qquad(\text{égalité 1})$$

Ce qui donne alors : $$\boxed{n_{_{Al}}=\dfrac{2\times n_{_{S}}}{3}}$$

A.N : $n_{_{Al}}=\dfrac{2\times 1}{3}=0.66$

D'où, $$\boxed{n_{_{Al}}=0.66\;mol}$$

Déterminons alors la quantité de sulfure d'aluminium $\left( Al_{2}S_{3}\right)$ qui serait formée.

En partant toujours de l'équation bilan de la réaction, on a les correspondances suivantes :

$$\begin{array}{rcl} 3\;moles_{_{(S)}}&\longrightarrow&1\;mole_{_{(Al_{2}S_{3})}}\\n_{_{S}}&\longrightarrow&n_{_{Al_{2}S_{3}}}\end{array}$$

Ce qui se traduit par :

$$\dfrac{n_{_{S}}}{3}=\dfrac{n_{_{Al_{2}S_{3}}}}{1}\qquad(\text{égalité 2})$$

Par suite, $$\boxed{n_{_{Al_{2}S_{3}}}=\dfrac{n_{_{S}}}{3}}$$

A.N : $n_{_{Al_{2}S_{3}}}=\dfrac{1}{3}=0.33$

Ainsi, $$\boxed{n_{_{Al_{2}S_{3}}}=0.33\;mol}$$

2) On veut former $0.50\;mol$ de sulfure d'aluminium $\left( Al_{2}S_{3}\right).$

Déterminons la quantité minimale d'aluminium et de soufre qu'il faut utiliser.

$-\ \ $ quantité minimale de soufre :

En considérant l'égalité (2), on a : $\dfrac{n_{_{S}}}{3}=\dfrac{n_{_{Al_{2}S_{3}}}}{1}$

Par suite, $$\boxed{n_{_{S}}=3n_{_{Al_{2}S_{3}}}}$$

A.N : $n_{_{S}}=3\times 0.50=1.5$

Ainsi, $$\boxed{n_{_{S}}=1.5\;mol}$$

$-\ \ $ quantité minimale d'aluminium :

D'après l'égalité (1), on obtient : $\dfrac{n_{_{Al}}}{2}=\dfrac{n_{_{S}}}{3}$

Donc, $$\boxed{n_{_{Al}}=\dfrac{2\times n_{_{S}}}{3}}$$

avec $\ n_{_{S}}=1.5\;mol$

A.N : $n_{_{Al}}=\dfrac{2\times 1.5}{3}=1$

Ainsi, $$\boxed{n_{_{Al}}=1\;mol}$$

Exercice 9 Bilan massique

Pour souder des rails de chemin de fer, on utilise l'aluminothermie.

Un mélange d'aluminium et d'oxyde de fer $\left(Fe_{2}O_{3}\right)$, placé entre les deux rails à souder, est enflammé.

Il se forme du fer et de l'oxyde d'aluminium $Al_{2}O_{3}.$

1) Écrivons l'équation bilan de la réaction chimique.

L'équation de la réaction étant donnée par :

$$Al\ +\ Fe_{2}O_{3}\ \rightarrow\ Fe\ +\ Al_{2}O_{3}$$

Alors, en équilibrant cette équation, on obtient l'équation bilan suivante :

$$2Al\ +\ Fe_{2}O_{3}\ \rightarrow\ 2Fe\ +\ Al_{2}O_{3}$$

2) On veut obtenir $112\;g$ de fer.

Pour cela, calculons la masse minimale d'oxyde de fer $\left(Fe_{2}O_{3}\right)$ et d'aluminium que l'on doit employer.

$-\ \ $ masse de $\left(Fe_{2}O_{3}\right)$

D'après l'équation bilan de la réaction, on a :

$$\begin{array}{rcl} 1\;mole_{_{(Fe_{2}O_{3})}}&\longrightarrow&2\;moles_{_{(Fe)}}\\n_{_{Fe_{2}O_{3}}}&\longrightarrow&n_{_{Fe}}\end{array}$$

Ce qui conduit à :

$$\dfrac{n_{_{Fe_{2}O_{3}}}}{1}=\dfrac{n_{_{Fe}}}{2}$$

Par suite, $$\boxed{n_{_{Fe_{2}O_{3}}}=\dfrac{n_{_{Fe}}}{2}}\quad(\text{égalité 1})$$

Or, on sait que : $n_{_{Fe_{2}O_{3}}}=\dfrac{m_{_{Fe_{2}O_{3}}}}{M_{_{Fe_{2}O_{3}}}}\ $ et $\ n_{_{Fe}}=\dfrac{m_{_{Fe}}}{M_{_{Fe}}}$

Ainsi, en remplaçant ces expressions de $n_{_{Fe_{2}O_{3}}}\ $ et $\ n_{_{Fe}}$ dans l'égalité (1), on trouve :

$\dfrac{m_{_{Fe_{2}O_{3}}}}{M_{_{Fe_{2}O_{3}}}}=\dfrac{\dfrac{m_{_{Fe}}}{M_{_{Fe}}}}{2}=\dfrac{m_{_{Fe}}}{2\times M_{_{Fe}}}$

Par suite,

$$\boxed{m_{_{Fe_{2}O_{3}}}=\dfrac{m_{_{Fe}}\times M_{_{Fe_{2}O_{3}}}}{2\times M_{_{Fe}}}}$$

Avec, $\ M_{_{Fe}}=56\;g.mol^{-1}\;;\;\ M_{_{Al}}=27\;g.mol^{-1}\;;\;\ M_{_{O}}=16\;g.mol^{-1}\ $ et

$\begin{array}{rcl} M_{_{Fe_{2}O_{3}}}&=&2M_{_{Fe}}+3M_{_{O}}\\ \\&=&2\times 56+3\times 16\\ \\&=&160\;g.mol^{-1}\end{array}$

A.N : $m_{_{Fe_{2}O_{3}}}=\dfrac{112\times 160}{2\times 56}=160$

D'où, $$\boxed{m_{_{Fe_{2}O_{3}}}=160\;g}$$

$-\ \ $ masse d'aluminium

En se référant encore à l'équation bilan de la réaction, on obtient :

$$\begin{array}{rcl} 2\;moles_{_{(Al)}}&\longrightarrow&2\;moles_{_{(Fe)}}\\n_{_{Al}}&\longrightarrow&n_{_{Fe}}\end{array}$$

Ainsi :

$$\dfrac{n_{_{Al}}}{2}=\dfrac{n_{_{Fe}}}{2}$$

Par suite, $$\boxed{n_{_{Fe_{2}O_{3}}}=n_{_{Fe}}}\quad(\text{égalité 2})$$

Comme $n_{_{Al}}=\dfrac{m_{_{Al}}}{M_{_{Al}}}\ $ et $\ n_{_{Fe}}=\dfrac{m_{_{Fe}}}{M_{_{Fe}}}$ alors, en remplaçant ces expressions de $n_{_{Al}}\ $ et $\ n_{_{Fe}}$ dans l'égalité (2), on trouve :

$$\dfrac{m_{_{Al}}}{M_{_{Al}}}=\dfrac{m_{_{Fe}}}{M_{_{Fe}}}$$

D'où,

$$\boxed{m_{_{Al}}=\dfrac{m_{_{Fe}}\times M_{_{Al}}}{M_{_{Fe}}}}$$

A.N : $m_{_{Al}}=\dfrac{112\times 27}{56}=54$

Ainsi, $$\boxed{m_{_{Al}}=54\;g}$$

Exercice 10 Bilan massique

Pour l'industrie du bâtiment, on fabrique de l'oxyde de calcium $(CaO)$, ou chaux vive, en chauffant du calcaire ou carbonate de calcium $\left(CaCO_{3}\right)$ dans de grands fours.

L'équation de la réaction est la suivante :

$$CaCO_{3}\quad\rightarrow\quad CaO\quad+\quad CO_{2}$$

1) Déterminons la masse de carbonate de calcium qu'il faudra transformer pour obtenir une tonne de chaux vive

D'après l'équation bilan de la réaction, on a :

$$\begin{array}{rcl} 1\;mole_{_{(CaCO_{3})}}&\longrightarrow&1\;mole_{_{(CaO)}}\\n_{_{CaCO_{3}}}&\longrightarrow&n_{_{CaO}}\end{array}$$

D'où, la correspondance suivante :

$$\dfrac{n_{_{CaCO_{3}}}}{1}=\dfrac{n_{_{CaO}}}{1}$$

Par suite, $$\boxed{n_{_{CaCO_{3}}}=n_{_{CaO}}}\quad(\text{égalité 1})$$

Comme $n_{_{CaCO_{3}}}=\dfrac{m_{_{CaCO_{3}}}}{M_{_{CaCO_{3}}}}\ $ et $\ n_{_{CaO}}=\dfrac{m_{_{CaO}}}{M_{_{CaO}}}$ alors, en remplaçant ces expressions de $n_{_{CaCO_{3}}}\ $ et $\ n_{_{CaO}}$ dans l'égalité (1), on trouve : $\dfrac{m_{_{CaCO_{3}}}}{M_{_{CaCO_{3}}}}=\dfrac{m_{_{CaO}}}{M_{_{CaO}}}$

Ce qui donne alors :

$$\boxed{m_{_{CaCO_{3}}}=\dfrac{m_{_{CaO}}\times M_{_{CaCO_{3}}}}{M_{_{CaO}}}}$$

avec ;

$\begin{array}{rcl} M_{_{CaCO_{3}}}&=&M_{_{Ca}}+M_{_{C}}+M_{_{O_{3}}}\\&=&40+12+3\times 16\\&=&100\;g.mol^{-1}\end{array}$

$\begin{array}{rcl} M_{_{CaO}}&=&M_{_{Ca}}+M_{_{O}}\\&=&40+16\\&=&56\;g.mol^{-1}\end{array}$

$m_{_{CaO}}=1\;t=1000\;kg=10^{6}\;g$

A.N : $m_{_{CaCO_{3}}}=\dfrac{10^{6}\times 100}{56}=1785714.285\;g$

Soit : $$\boxed{m_{_{CaCO_{3}}}=1.786\;t}$$

2) Masse de dioxyde de carbone obtenu

En considérant encore l'équation bilan de la réaction, on obtient :

$$\begin{array}{rcl} 1\;mole_{_{(CaO)}}&\longrightarrow&1\;mole_{_{(CO_{2})}}\\n_{_{CaO}}&\longrightarrow&n_{_{CO_{2}}}\end{array}$$

Ainsi,

$$\dfrac{n_{_{CaO}}}{1}=\dfrac{n_{_{CO_{2}}}}{1}$$

Par suite, $$\boxed{n_{_{CaO}}=n_{_{CO_{2}}}}\quad(\text{égalité 2})$$

Or, on sait que : $n_{_{CaO}}=\dfrac{m_{_{CaO}}}{M_{_{CaO}}}\ $ et $\ n_{_{CO_{2}}}=\dfrac{m_{_{CO_{2}}}}{M_{_{CO_{2}}}}$ donc, en reportant dans l'égalité (2), on trouve : $\dfrac{m_{_{CaO}}}{M_{_{CaO}}}=\dfrac{m_{_{CO_{2}}}}{M_{_{CO_{2}}}}$

Ce qui donne alors :

$$\boxed{m_{_{CO_{2}}}=\dfrac{m_{_{CaO}}\times M_{_{CO_{2}}}}{M_{_{CaO}}}}$$

avec

$\begin{array}{rcl} M_{_{CO_{2}}}&=&M_{_{C}}+M_{_{O_{2}}}\\&=&12+2\times 16\\&=&44\;g.mol^{-1}\end{array}$

$M_{_{CaO}}=56\;g.mol^{-1}\quad\text{et}\quad m_{_{CaO}}=1\;t=1000\;kg=10^{6}\;g$

A.N : $m_{_{CO_{2}}}=\dfrac{10^{6}\times 44}{56}=785714.285\;g$

Soit : $$\boxed{m_{_{CO_{2}}}=0.786\;t}$$

3) Le processus de fabrication de l'oxyde de calcium $(CaO)$, libère du gaz carbonique $(CO_{2})$ dans l'atmosphère entraînant ainsi, le réchauffement climatique.

En effet, le gaz carbonique $(CO_{2})$ est un gaz à effet de serre qui contribue à réguler la température de la planète en retenant les rayons infrarouges émis par le soleil dans l'atmosphère.

Cependant, une augmentation due à l'activité humaine peut provoquer un dérèglement de cet équilibre naturel. Ce qui, en conséquence, entraînera une élévation de la température de la planète.

Exercice 11 Bilan volumique

Le dioxyde de soufre $(SO_{2})$ réagit avec le sulfure d'hydrogène $(HS)$ selon l'équation-bilan :

$$SO_{2}\ +\ 2H_{2}S\ \rightarrow\ 3S\ +\ 2H_{2}O$$

Le dioxyde de soufre et le sulfure d'hydrogène sont à l'état gazeux.

1) Déterminons le volume de sulfure d'hydrogène nécessaire à la transformation de $1.5\;l$ de dioxyde de soufre.

En considérant l'équation-bilan de la réaction, on obtient :

$$\begin{array}{rcl} 1\;mole_{_{(SO_{2})}}&\longrightarrow&2\;moles_{_{(H_{2}S)}}\\n_{_{SO_{2}}}&\longrightarrow&n_{_{H_{2}S}}\end{array}$$

D'où, la correspondance suivante :

$$\dfrac{n_{_{SO_{2}}}}{1}=\dfrac{n_{_{H_{2}S}}}{2}$$

Par suite,

$$\boxed{n_{_{H_{2}S}}=2n_{_{SO_{2}}}}\quad(\text{égalité *})$$

Or, on sait que : $n_{_{H_{2}S}}=\dfrac{V_{_{H_{2}S}}}{V_{_{M}}}\ $ et $\ n_{_{SO_{2}}}=\dfrac{V_{_{SO_{2}}}}{V_{_{M}}}$ donc, en reportant dans l'égalité (*), on trouve : $\dfrac{V_{_{H_{2}S}}}{V_{_{M}}}=2\dfrac{V_{_{SO_{2}}}}{V_{_{M}}}$

Ce qui donne : $V_{_{H_{2}S}}=\dfrac{2\times V_{_{SO_{2}}}\times V_{_{M}}}{V_{_{M}}}$

Par conséquent,

$$\boxed{V_{_{H_{2}S}}=2\times V_{_{SO_{2}}}}$$

Application numérique : $V_{_{H_{2}S}}=2\times 1.5=3$

Donc, $\boxed{V_{_{H_{2}S}}=3\;l}$

2) Déterminons la masse de soufre que l'on peut préparer par ce procédé en faisant réagir $1.25\;m^{3}$ de dioxyde de soufre.

D'après l'équation-bilan de la réaction, on a :

$$\begin{array}{rcl} 1\;mole_{_{(SO_{2})}}&\longrightarrow&3\;moles_{_{(S)}}\\n_{_{SO_{2}}}&\longrightarrow&n_{_{S}}\end{array}$$

Par suite,

$$\dfrac{n_{_{SO_{2}}}}{1}=\dfrac{n_{_{S}}}{3}$$

D'où,

$$\boxed{n_{_{S}}=3n_{_{SO_{2}}}}\quad(\text{égalité **})$$

Comme $n_{_{S}}=\dfrac{m_{_{S}}}{M_{_{S}}}\ $ et $\ n_{_{SO_{2}}}=\dfrac{V_{_{SO_{2}}}}{V_{_{M}}}$ alors, en remplaçant dans l'égalité (**), on obtient : $\dfrac{m_{_{S}}}{M_{_{S}}}=3\dfrac{V_{_{SO_{2}}}}{V_{_{M}}}$

Ce qui donne :

$$\boxed{m_{_{S}}=\dfrac{3\times V_{_{SO_{2}}}\times M_{_{S}}}{V_{_{M}}}}$$

avec : $V_{_{SO_{2}}}=1.25\;m^{3}=1.25\cdot 10^{3}\;l\;;\ M(S)=32\;g.mol^{-1}\;;\ V_{M}=24\;l.mol^{-1}$

Application numérique : $m_{_{S}}=\dfrac{3\times 1.25\cdot 10^{3}\times 32}{24}=5\cdot 10^{3}$

Ainsi, $\boxed{m_{_{S}}=5\cdot 10^{3}\;g=5\;kg}$

Exercice 12 Bilan massique et volumique

Le magnésium $(Mg)$ brule dans l'air en donnant de l'oxyde magnésium $(MgO).$

1) Écrivons l'équation bilan de la réaction.

$$Mg\ +\ \dfrac{1}{2}O_{2}\ \rightarrow\ MgO$$

2) Calculons le volume de dioxygène nécessaire à la combustion de $2.4\;g$ de magnésium.

D'après l'équation-bilan de la réaction, on a :

$$\begin{array}{rcl} 1\;mole_{_{(Mg)}}&\longrightarrow&\dfrac{1}{2}\;moles_{_{(O_{2})}}\\n_{_{Mg}}&\longrightarrow&n_{_{O_{2}}}\end{array}$$

D'où, la correspondance suivante : $\dfrac{n_{_{Mg}}}{1}=\dfrac{n_{_{O_{2}}}}{\dfrac{1}{2}}$

Ce qui donne : $\dfrac{n_{_{Mg}}}{1}=\dfrac{2n_{_{O_{2}}}}{1}$

Soit :

$$\boxed{n_{_{O_{2}}}=\dfrac{1}{2}n_{_{Mg}}}\quad(\text{égalité 1})$$

Or, on sait que : $n_{_{Mg}}=\dfrac{m_{_{Mg}}}{M_{_{Mg}}}\ $ et $\ n_{_{O_{2}}}=\dfrac{V_{_{O_{2}}}}{V_{_{M}}}.$

Donc, en reportant ces expressions de $n_{_{O_{2}}}\ $ et $\ n_{_{Mg}}$ dans l'égalité (1), on obtient : $\dfrac{V_{_{O_{2}}}}{V_{_{M}}}=\dfrac{1}{2}\times\dfrac{m_{_{Mg}}}{M_{_{Mg}}}$

Par suite,

$$\boxed{V_{_{O_{2}}}=\dfrac{m_{_{Mg}}\times V_{_{M}}}{2\times M_{_{Mg}}}}$$

Application numérique : $V_{_{O_{2}}}=\dfrac{2.4\times 24}{2\times 24}=1.2$

D'où, $\boxed{V_{_{O_{2}}}=1.2\;l}$

En déduisons le volume d'air utilisé.

Comme l'air sec contient en volume $21\%$ de dioxygène alors, le volume d'air $V_{\text{air}}$ utilisé dans la combustion de $2.4\;g$ de magnésium est tel que :

$$V_{_{O_{2}}}=\dfrac{21}{100}\times V_{\text{air}}$$

Par suite,

$$\boxed{V_{\text{air}}=\dfrac{100}{21}\times V_{_{O_{2}}}}$$

Application numérique : $V_{\text{air}}=\dfrac{100}{21}\times 1.2=5.71$

Ainsi, $\boxed{V_{\text{air}}=5.71\;l}$

3) Calculons la masse de l'oxyde de magnésium obtenue.

D'après l'équation-bilan de la réaction, on a :

$$\begin{array}{rcl} 1\;mole_{_{(Mg)}}&\longrightarrow&1\;mole_{_{(MgO)}}\\n_{_{Mg}}&\longrightarrow&n_{_{MgO}}\end{array}$$

D'où, la correspondance suivante : $\dfrac{n_{_{Mg}}}{1}=\dfrac{n_{_{MgO}}}{1}$

Soit :

$$\boxed{n_{_{MgO}}=n_{_{Mg}}}\quad(\text{égalité 2})$$

Comme $n_{_{MgO}}=\dfrac{m_{_{MgO}}}{M_{_{MgO}}}\ $ et $\ n_{_{Mg}}=\dfrac{m_{_{Mg}}}{M_{_{Mg}}}$ alors, en remplaçant dans l'égalité (2), on obtient : $\dfrac{m_{_{MgO}}}{M_{_{MgO}}}=\dfrac{m_{_{Mg}}}{M_{_{Mg}}}$

Ce qui donne alors,

$$\boxed{m_{_{MgO}}=\dfrac{m_{_{Mg}}\times M_{_{MgO}}}{M_{_{Mg}}}}$$

avec ; $M_{_{MgO}}=M_{_{Mg}}M_{_{O}}=24+16=40\;g.mol^{-1}$

Application numérique : $m_{_{MgO}}=\dfrac{2.4\times 40}{24}=4$

Soit : $\boxed{m_{_{MgO}}=4\;g}$

Exercice supplémentaire

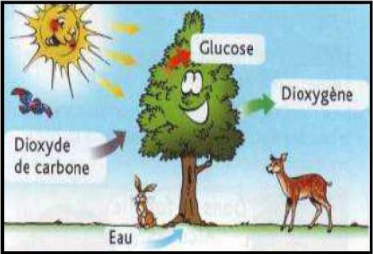
La photosynthèse permet aux plantes d'utiliser l'énergie solaire afin de fabriquer les substances qui leur sont indispensables pour vivre.

Les nutriments nécessaires à la plante sont, entre autres, le dioxyde de carbone et l'eau.

C'est une transformation chimique qui conduit à la formation de glucose $(C_{6}H_{12}O_{6})$ et de dioxygène.

Pendant la nuit, la photosynthèse n'a plus lieu, la plante respire comme toute autre être vivant.

1) Par définition, une transformation chimique est une transformation au cours de laquelle des corps purs réagissent et disparaissent pour laisser apparaitre d'autres corps purs.

Or, la photosynthèse est un processus qui, sous l'effet de l'énergie solaire, fait réagir et disparaitre du dioxyde de carbone et de l'eau ; deux corps purs, pour produire du glucose $(C_{6}H_{12}O_{6})$ et du dioxygène.

C'est pourquoi on dit que la photosynthèse est une transformation chimique.

2) Les noms et les formules des réactifs mis en jeu dans la photosynthèse sont donnés dans le tableau suivant :

$$\begin{array}{|l|c|}\hline\text{nom}&\text{formule}\\ \hline\text{dioxyde de carbone}&CO_{2}\\ \hline\text{eau}&H_{2}O\\ \hline \end{array}$$

3) Les noms et les formules des produits formés sont donnés dans le tableau suivant :

$$\begin{array}{|l|c|}\hline\text{nom}&\text{formule}\\ \hline\text{glucose}&C_{6}H_{12}O_{6}\\ \hline\text{dioxygène}&O_{2}\\ \hline \end{array}$$

4) L'équation de cette réaction est :

$$CO_{2}\ +\ H_{2}O\ \rightarrow\ C_{6}H_{12}O_{6}\ +\ O_{2}$$

En équilibrant cette équation, on obtient l'équation-bilan suivante :

$$6CO_{2}\ +\ 6H_{2}O\ \rightarrow\ C_{6}H_{12}O_{6}\ +\ 6O_{2}$$

5) Une déforestation massive entraîne une disparition massive des arbres.

Or, ces arbres, à travers la réaction de photosynthèse, produisent du dioxygène qui est un gaz respiratoire indispensable à la vie.

Par conséquent, une déforestation massive peut entraîner une diminution considérable voire même une raréfaction de l'oxygène dans la nature.

Ce qui rendrait la vie impossible ; sans oxygène l'homme les animaux ne peuvent vivre sur terre.

D'où, cette inquiétude sur une quelconque déforestation massive.

Auteur:

Aliou ndiaye

Commentaires

Anonyme (non vérifié)

ven, 06/05/2020 - 15:22

Permalien

Vomool

Thttdr

répondre

Thierno mouhama... (non vérifié)

mer, 12/16/2020 - 17:58

Permalien

Enregistrer cette page

répondre

Anonyme (non vérifié)

ven, 10/18/2024 - 19:39

Permalien

Pour tout ce qu'il faut

répondre

Mens (non vérifié)

jeu, 04/22/2021 - 11:55

Permalien

Salut

Excellent

répondre

Khadija sabaly (non vérifié)

ven, 05/31/2024 - 00:26

Permalien

Réussir

En travaillant

répondre

Anonyme (non vérifié)

dim, 06/13/2021 - 19:46

Permalien

J'ai bien compris

répondre

Doza denish (non vérifié)

dim, 07/04/2021 - 22:43

Permalien

J'ai très bien compris et

J'ai très bien compris et tout çà grâce à vous. Je vous remercie beaucoup et je vous souhaite une bonne continuation❤❤❤❤❤

répondre

Anonyme (non vérifié)

sam, 06/01/2024 - 22:47

Permalien

J ai compris grace a

J ai compris grace a sunudaara C est une opportunité pour tous les élèves

répondre

Doza denish (non vérifié)

dim, 07/04/2021 - 22:43

Permalien

J'ai très bien compris et

J'ai très bien compris et tout çà grâce à vous. Je vous remercie beaucoup et je vous souhaite une bonne continuation❤❤❤❤❤

répondre

Diop (non vérifié)

sam, 06/11/2022 - 23:00

Permalien

SP

Je vous remercie au fond du cœur ❤

répondre

Fatou ba (non vérifié)

mar, 07/13/2021 - 00:47

Permalien

Merci.

répondre

M. Insa SANE Pr... (non vérifié)

mer, 07/14/2021 - 13:38

Permalien

Fichiers des solutions aux exercices

Bonjour chers Collègues. Félicitations pour cet excellent travail que vous avez réalisé. Je souhaiterais recevoir, si possible, les fichiers contenant les solutions aux exercices proposés. Je vous donne mon adresse e-mail: insasane53@yahoo.fr Je vous saurais gré de bien vouloir me les envoyer à cette adresse e-mail ou me donner un site où je pourrai les télécharger. Merci d'avance chers Collègues.