Solution des exercices : Repérage sur une droite et dans le plan - 6e
Classe:
Sixième
Exercice 1
On considère la droite graduée suivante :

1) Déterminons graphiquement les abscisses des points : $A\;;\ B\;;\ I\;;\ M\;;\ N\ $ et $\ P.$
Pour cela, on identifie sur la droite graduée l'abscisse qui correspond à la position de chaque point.

Ainsi :
$A$ a pour abscisse $2$
$B$ a pour abscisse $-2$
$I$ a pour abscisse $1.5$
$M$ a pour abscisse $4.5$
$N$ a pour abscisse $-4$
$P$ a pour abscisse $4$
2) Plaçons les points : $K\;;\ L\ $ et $\ Q$ d'abscisses respectives : $-3\;;\ -0.5\ $ et $\ +3.5$
On marque alors les valeurs $-3\;;\ -0.5\ $ et $\ +3.5$ sur la même droite graduée.
Ces valeurs vont donc correspondre aux positions respectives des points $K\;;\ L\ $ et $\ Q.$

Exercice 2
1) Sur une droite graduée $(xx')$ d'unité $1\;cm$ , d'origine $O$, plaçons les points : $A\;;\ B\;;\ C\ $ et $\ D$ d'abscisses respectives : $-4\;;\ -2.5\;;\ +2\ $ et $\ 3.5$

2) Déterminons les distances : $OA\;;\ OB\;;\ OC\ $ et $\ OD.$
On a $O$ origine du repère et $A$ d'abscisse $-4$ alors : $OA=|-4|=4$
Donc, $\boxed{OA=4\;cm}$
Soit $B$ d'abscisse $-2.5$ et $O$ origine du repère alors, on a :
$OB=|-2.5|=2.5$
Ainsi, $\boxed{OB=2.5\;cm}$
On a : $C$ d'abscisse $+2$ et $O$ origine du repère donc, $OC=|+2|=2$
Par suite, $\boxed{OC=2\;cm}$
Soit $D$ d'abscisse $3.5$ et $O$ origine du repère alors, on a : $OD=|3.5|=3.5$
D'où, $\boxed{OD=3.5\;cm}$
3) En déduisons les distances $AC\ $ et $\ BD.$
En observant le graphique, on peut dire que la distance $AC$ est égale la somme des distances $AO\ $ et $\ OC.$
Or, $AO=OA$ donc en changeant $AO$ par $OA$, on obtient : $AC=OA+OC$
Comme, $OA=4\;cm\ $ et $\ OC=2\;cm$ alors, $AC=4\;cm+2\;cm=6\;cm$
D'où, $\boxed{AC=6\;cm}$
De la même manière, on peut écrire : $BD=BO+OD$
Or, $BO=OB$ donc en remplaçant $BO$ par $OB$, on obtient : $BD=OB+OD$
Comme $OB=2.5\;cm\ $ et $\ OD=3.5\;cm$ alors, on obtient :
$BD=2.5\;cm+3.5\;cm=6\;cm$
Ainsi, $\boxed{BD=6\;cm}$
Exercice 3
On considère le repère orthonormal ci-dessous.
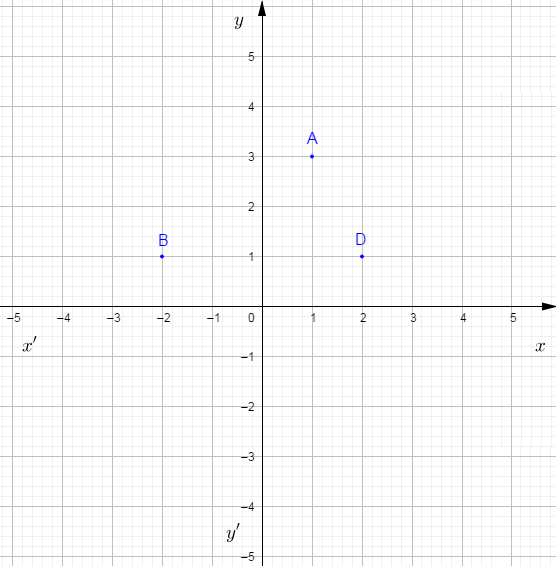
1) Déterminons graphiquement les coordonnées des points $A\;;\ B\ $ et $\ D.$
Pour déterminer graphiquement les coordonnées du point $A$, on procède comme suit :
A partir du point $A$, on trace une ligne rouge parallèle à l'axe $(yy').$
Cette ligne coupe l'axe $(xx')$ à la valeur $1.$
Donc, $1$ est l'abscisse du point $A.$
On procède de la même manière pour déterminer l'ordonnée du point $A.$
Ainsi, à partir de $A$, on trace une ligne rouge parallèle à l'axe $(xx').$
Cette ligne coupe l'axe $(yy')$ à la valeur $3.$
Par suite, $3$ est l'ordonnée du point $A.$
Par conséquent, $A(1\;;\ 3)$
On procède de la même manière pour déterminer les coordonnés des points $B\ $ et $\ D.$
Ainsi, on obtient : $B(-2\;;\ 1)\ $ et $\ D(2\;;\ 1)$
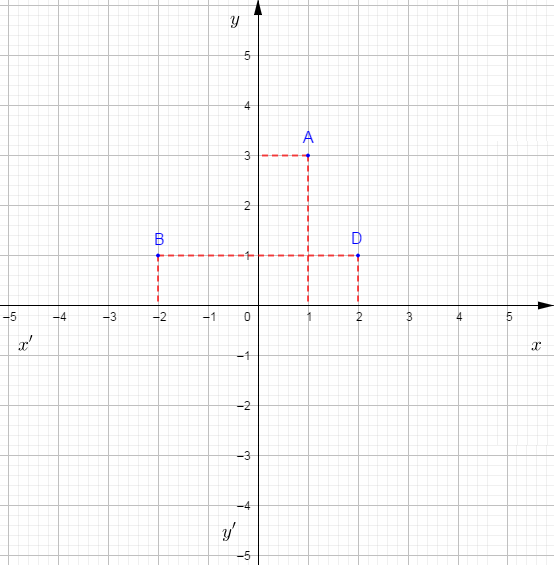
2) Plaçons les points : $C(+2\;;\ +3)\ $ et $\ E(-3.5\;;\ -2).$
Pour placer le $C$ dans le repère, on marque l'abscisse $2$ et on trace une ligne verte parallèle à l'axe $(yy').$
De même, on identifie l'ordonnée $3$ et on trace une ligne verte parallèle à l'axe $(xx').$
Les deux lignes vertes se coupent au point $C.$
On place alors le point $C.$
On procède de la même manière pour placer le point $E.$
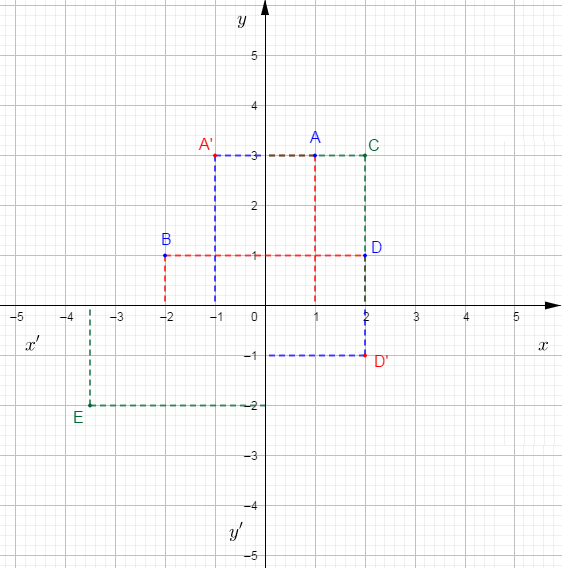
3) a) Construisons le point $A'$ symétrique de $A$ par rapport à $(yy').$
b) Déterminons graphiquement les coordonnées de $A'.$
Pour cela, on procède comme dans la question 1).
On trouve alors : $A'(-1\;;\ 3)$
4) a) Construisons le point $D'$ symétrique de $D$ par rapport à $(xx').$
b) Déterminons graphiquement les coordonnées de $D'.$
En procédant de la manière que dans la question 1), on obtient : $D'(2\;;\ -1)$
Exercice 4
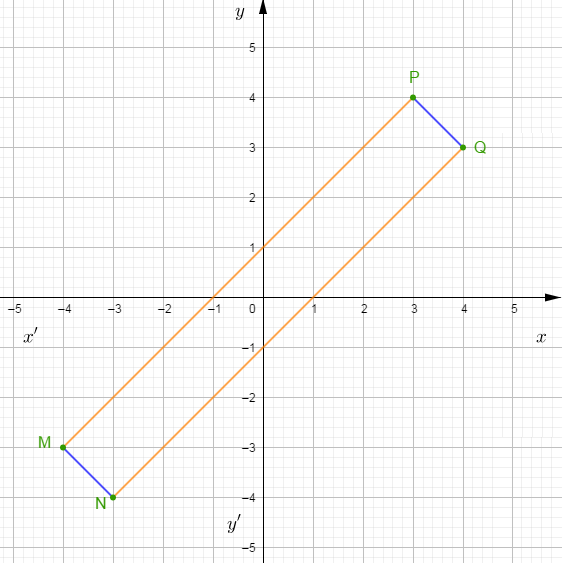
1) Dans un repère orthonormé, marquons les points : $M(-4\;;\ -3)\;;\ N(-3\;;\ -4)\;;\ P(+3\;;\ +4)\ $ et $\ Q(+4\;;\ +3).$
2) Le quadrilatère $MNPQ$ est un parallélogramme.
Exercice 5
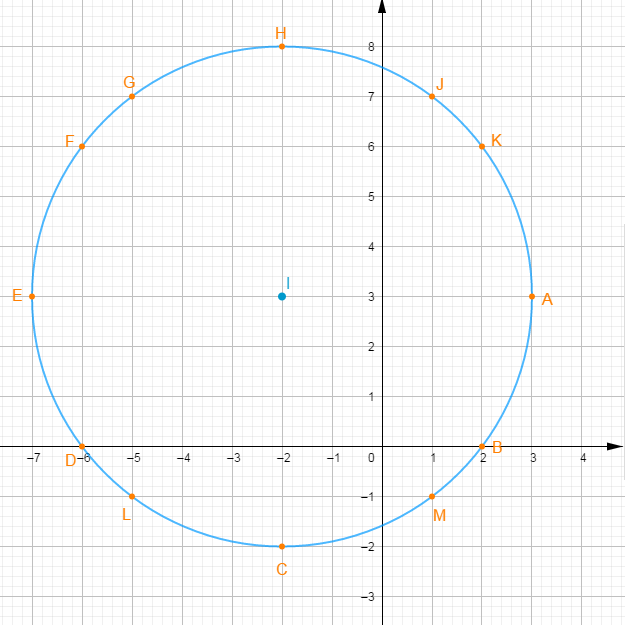
1) Dans un repère orthonormé, marquons le point $I(-2\;;\ +3).$
2) Traçons le cercle de centre $I$ de $5\;cm$ de rayon.
3) Les points suivants sont des points du cercle dont les coordonnées sont des entiers relatifs : $A\;,\ B\;,\ C\;,\ D\;,\ E\;,\ F\;,\ G\;,\ H\;,\ J\;,\ K\;,\ L\ $ et $\ M$
Leurs coordonnées sont données par :
$A(+3\;;\ +3)\;,\ B(+2\;;\ 0)\;,\ C(-2\;;\ -2)\;,\ D(-6\;;\ 0)$
$E(-7\;;\ +3)\;,\ F(-6\;;\ +6)\;,\ G(-5\;;\ +7)\;,\ H(-2\;;\ +8)$
$J(+1\;;\ +7)\;,\ K(+2\;;\ +6)\;,\ (-5\;;\ -1)\;,\ M(+1\;;\ -1)$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
mer, 06/07/2023 - 00:28
Permalien
Hh
Ajouter un commentaire