Vous êtes ici

Équations à une inconnue dans Q - 4e

Classe:

Quatrième

I. Activité

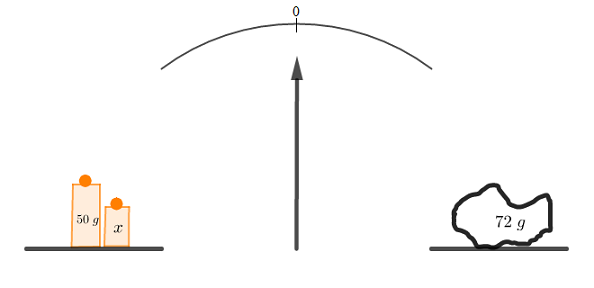
On réalise l'équilibre ci-dessus à l'aide d'une balance. Un objet de masse

$x$ et une masse marquée de

$50\;g$ sont en équilibre avec un corps de masse

$72\;g.$

L'équilibre de la balance traduit une égalité entre les masses.

On obtient ainsi une équation à une inconnue

$s.$

$\centerdot\ x+5$ est le premier membre de l'équation.

$\centerdot\ 72$ est le second membre de l'équation.

Donc, l'équation est :

$x+50=72$

II. Définition et exemples

II.1. Définition

On appelle équation à une inconnue toute égalité dans laquelle se trouve une inconnue.

II.2. Exemples

$x+3=5$ ; ici

$x$ est l'inconnue

$2t=0$ ; c'est une équation d'inconnue

$t$

$\dfrac{2}{y}=\dfrac{1}{5}$ ; dans cette équation,

$y$ est l'inconnue

$3z+4=-z-8$ ; pour cette équation, c'est

$z$ l'inconnue

$(3p-5)(p+2)=0$ ; dans cette équation,

$p$ est l'inconnue

III. Résolution d'équations

Résoudre une équation dans

$\mathbb{Q}$ revient à déterminer l'ensemble des nombres rationnels qui vérifient l'égalité.

Cet ensemble est appelé l'ensemble des solutions de l'équation.

On le note :

$S.$

Exemples

$\begin{array}{rcl} x+3=5&\Rightarrow&x=5-2\\ \\&\Rightarrow&x=2\end{array}$

D'où,

$S=\{2\}$

III.1. Équations se ramenant à la forme $ax+b=0$ avec $a\neq 0$

Activité 1

Soit un triangle

$ABC$ tel que :

$mes\;\widehat{BAC}$ est égale à

$x$ ;

$mes\;\widehat{ABC}$ est le double de

$mes\;\widehat{BAC}$ et est le triple de

$mes\;\widehat{ACB}.$

Trouver la mesure de

$\widehat{ABC}\;;\ \widehat{CAB}\$ et

$\ \widehat{BAC}.$

Solution

1) Choix de l'inconnu

Soit

$x$ la mesure de l'angle

$\widehat{BAC}$

On a :

$\left\lbrace\begin{array}{rcl} mes\;\widehat{ABC} &=& 2x \\ mes\;\widehat{ACB} &=& 3x \end{array}\right.$

2) Mise en équation

Dans un triangle, la somme des angles est égale à

$180^{\circ}$

Donc,

$x+2x+3x=180^{\circ}\;\Leftrightarrow\;6x=180^{\circ}$

3) Résolution

$\begin{array}{rcl} x+2x+3x=180^{\circ}&\Leftrightarrow&6x=180^{\circ}\\ \\ &\Leftrightarrow&x=\dfrac{180^{\circ}}{6}\\ \\ &\Leftrightarrow&x=30^{\circ}\end{array}$

Ainsi :

$mes\;\widehat{BAC}=30^{\circ}$

$mes\;\widehat{ABC}=2\times 30^{\circ}=60^{\circ}$

$mes\;\widehat{ACB}=3\times 30^{\circ}=90^{\circ}$

4) Vérification

$30^{\circ}+60^{\circ}+90^{\circ}=180^{\circ}$

Activité 2

La somme de

$3$ nombres entiers consécutifs est égale à

$96.$

Quels sont ces

$3$ entiers ?

Solution

1) Choix de l'inconnu

Soit

$x$ le premier nombre

Soit

$(x+1)$ le deuxième nombre

Soit

$((x+1)+1)=(x+2)$ le troisième nombre

2) Mise en équation

$x+(x+1)+(x+2)=96$

3) Résolution

$\begin{array}{rcl} x+(x+1)+(x+2)=96&\Leftrightarrow&3x+3=96\\ \\&\Leftrightarrow&3x=96-3\\ \\&\Leftrightarrow&x=\dfrac{93}{3}\\ \\&\Leftrightarrow&x=31\end{array}$

Par suite :

Le premier nombre est égal à :

$x=31$

Le deuxième nombre est donnée par :

$(x+1)=(31+1)=32$

Le troisième nombre est égal à :

$(x+2)=(31+2)=33$

4) Vérification

$31+32+33=96$

Soit l'équation :

$ax+b=0$ avec

$a\neq 0$

Alors, on a :

$ax+b=0$ si, et seulement si,

$ax=-b.$

Ce qui donne :

$x=\dfrac{-b}{a}$

D'où, l'ensemble des solutions

$S$ sera donné par :

$S=\left\lbrace\dfrac{-b}{a}\right\rbrace$

Remarque

$-\$ Si

$a=0\$ et

$\ b=0$ alors, l'équation devient

$0x=0$

D'où,

$S=\mathbb{Q}$

$-\$ Si

$a=0\$ et

$\ b\neq 0$ alors, l'équation devient

$0x=b.$ Impossible

D'où,

$S=\emptyset$

Exercice d'application

1) Résoudre dans

$\mathbb{Q}$ les équations suivantes :

$4x+12=127$

$2x-4=0$

$-7x-1=-3$

$\dfrac{3}{4}x+\dfrac{1}{2}=\dfrac{3}{2}$

2) Dans une classe de quatrième

$1/3$ écrit,

$1/4$ dessine,

$1/6$ calcule,

$1/10$ bavarde et les

$9$ restants sont absents.

Quel est l'effectif total de cette classe.

Solution

$\begin{array}{rcl} a)\ \ 4x+12=127&\Leftrightarrow&4x=127-12\\ \\ &\Leftrightarrow&4x=115\\ \\ &\Leftrightarrow&x=\dfrac{115}{4}\end{array}$

Ainsi,

$S=\left\lbrace\dfrac{115}{4}\right\rbrace$

$\begin{array}{rcl} b)\ \ 2x-4=0&\Leftrightarrow&2x=4\\ \\ &\Leftrightarrow&x=\dfrac{4}{2}\\ \\ &\Leftrightarrow&x=2\end{array}$

D'où,

$S=\left\lbrace 2\right\rbrace$

$\begin{array}{rcl} c)\ \ -7x-1=-3&\Leftrightarrow&-7x=-3+1\\ \\ &\Leftrightarrow&-7x=-2\\ \\ &\Leftrightarrow&x=\dfrac{-2}{-7}\\ \\ &\Leftrightarrow&x=\dfrac{2}{7}\end{array}$

Par suite,

$S=\left\lbrace\dfrac{2}{7}\right\rbrace$

$\begin{array}{rcl} d)\ \ \dfrac{3}{4}x+\dfrac{1}{2}=\dfrac{3}{2}&\Leftrightarrow&\dfrac{3}{4}x=\dfrac{3}{2}-\dfrac{1}{2}\\ \\ &\Leftrightarrow&\dfrac{3}{4}x=\dfrac{3-1}{2}\\ \\ &\Leftrightarrow&\dfrac{3}{4}x=\dfrac{2}{2}\\ \\ &\Leftrightarrow&\dfrac{3}{4}x=1\\ \\ &\Leftrightarrow&x=\dfrac{1}{\dfrac{3}{4}}\\ \\ &\Leftrightarrow&x=\dfrac{4}{3}\end{array}$

D'où,

$S=\left\lbrace\dfrac{4}{3}\right\rbrace$

Choix de l'inconnu

Soit

$x$ l'effectif total de cette classe. Alors :

$\dfrac{x}{3}=\dfrac{40x}{120}$ élèves écrivent,

$\dfrac{x}{4}=\dfrac{30x}{120}$ élèves dessinent,

$\dfrac{x}{6}=\dfrac{20x}{120}$ élèves calculent,

$\dfrac{x}{10}=\dfrac{12x}{120}$ élèves bavardent et les

$9$ restants sont absents.

Mise en équation

$x=\dfrac{40x}{120}+\dfrac{30x}{120}+\dfrac{20x}{120}+\dfrac{12x}{120}+9$

Ce qui donne :

$x=\dfrac{40x+30x+20x+12x}{120}+9=\dfrac{102x}{120}+9$

Résolution

$\begin{array}{rcl} x=\dfrac{102x}{120}+9&\Leftrightarrow&x-\dfrac{102x}{120}=9\\ \\&\Leftrightarrow&\dfrac{120x}{120}-\dfrac{102x}{120}=9\\ \\&\Leftrightarrow&\dfrac{120x-102x}{120}=9\\ \\&\Leftrightarrow&\dfrac{18x}{120}=9\\ \\&\Leftrightarrow&18x=9\times 120\\ \\&\Leftrightarrow&18x=1080\\ \\&\Leftrightarrow&x=\dfrac{1080}{18}\\ \\&\Leftrightarrow&x=60\end{array}$

Donc, cette classe de quatrième compte

$60$ élèves dont :

$\dfrac{60}{3}=20$ écrivent,

$\dfrac{60}{4}=15$ dessinent,

$\dfrac{60}{6}=10$ calculent,

$\dfrac{60}{10}=6$ bavardent et les

$9$ restants sont absents.

Vérification

$20+15+10+6+9=60$

III.2. Équations de la forme $(ax+b)(cx+d)=0$ et équation se ramenant à cette forme avec $a\neq 0\$ et $\ c\neq 0$

Règle : Un produit de facteur est nul si au moins l'un des facteurs est nul.

$(ax+b)(cx+d)=0\;\Leftrightarrow\;ax+b=0\;\text{ ou }\;cx+d=0$

Les deux équations sont résolues séparément.

Ce qui donne :

$ax=-b\$ ou

$\ cx=-d$

Par suite :

$x=\dfrac{-b}{a}\$ ou

$\ x=\dfrac{-d}{c}$

D'où, l'ensemble des solutions sera donné par :

$S=\left\lbrace\dfrac{-b}{a}\;;\ \dfrac{-d}{c}\right\rbrace$

Exercice d'application

Résoudre dans

$\mathbb{Q}$ les équations suivantes :

$(3x-7)(x+5)=0$

$(2x+3)(4x+1)=0$

$4x^{2}-25=0$

$(x-5)(2x-3)=(x-5)(4x-1)$

Solution

$\begin{array}{rcl}\text{a)}\ \ (3x-7)(x+5)=0&\Leftrightarrow&3x-7=0\ \text{ ou }\ x+5=0\\ \\ &\Leftrightarrow&3x=7\ \text{ ou }\ x=-5\\ \\ &\Leftrightarrow&x=\dfrac{7}{3}\ \text{ ou }\ x=-5\end{array}$

Ainsi,

$S=\left\lbrace\dfrac{7}{3}\;;\ -5\right\rbrace$

$\begin{array}{rcl}\text{b)}\ \ (2x+3)(4x+1)=0&\Leftrightarrow&2x+3=0\ \text{ ou }\ 4x+1=0\\ \\ &\Leftrightarrow&2x=-3\ \text{ ou }\ 4x=-1\\ \\ &\Leftrightarrow&x=\dfrac{-3}{2}\ \text{ ou }\ x=\dfrac{-1}{4}\end{array}$

D'où,

$S=\left\lbrace\dfrac{-3}{2}\;;\ \dfrac{-1}{4}\right\rbrace$

c) Pour résoudre l'équation

$4x^{2}-25=0$ , on factorise d'abord l'expression

$4x^{2}-25$

On a :

$4x^{2}-25=(2x)^{2}-(5)^{2}=(2x-5)(2x+5)$

Par suite,

$\begin{array}{rcl} 4x^{2}-25=0&\Leftrightarrow&(2x-5)(2x+5)=0\\ \\&\Leftrightarrow&2x-5=0\ \text{ ou }\ 2x+5=0\\ \\ &\Leftrightarrow&2x=5\ \text{ ou }\ 2x=-5\\ \\ &\Leftrightarrow&x=\dfrac{5}{2}\ \text{ ou }\ x=\dfrac{-5}{2}\end{array}$

Ainsi,

$S=\left\lbrace\dfrac{5}{2}\;;\ \dfrac{-5}{2}\right\rbrace$

d) On a :

$(x-5)(2x-3)=(x-5)(4x-1)$ si, et seulement si,

$(x-5)(2x-3)-(x-5)(4x-1)=0$

En factorisant, on obtient :

$\begin{array}{rcl} (x-5)(2x-3)-(x-5)(4x-1)&=&(x-5)[(2x-3)-(4x-1)]\\ \\&=&(x-5)(2x-3-4x+1)\\ \\&=&(x-5)(-2x-2)\end{array}$

Donc,

$\begin{array}{rcl} (x-5)(2x-3)-(x-5)(4x-1)=0&\Leftrightarrow&(x-5)(-2x-2)=0\\ \\&\Leftrightarrow&x-5=0\ \text{ ou }\ -2x-2=0\\ \\ &\Leftrightarrow&x=5\ \text{ ou }\ -2x=2\\ \\ &\Leftrightarrow&x=5\ \text{ ou }\ x=\dfrac{2}{-2}\\ \\ &\Leftrightarrow&x=5\ \text{ ou }\ x=-1\end{array}$

D'où,

$S=\left\lbrace 5\;;\ -1\right\rbrace$

III.3. Équations de type $\dfrac{a}{x}=b\;;\ \dfrac{a}{x}=\dfrac{b}{c}$ avec $c\neq 0\$ et $\ x\neq 0$

On a :

$\dfrac{a}{x}=\dfrac{b}{c}$ si, et seulement si,

$a\times c=b\times x$

Ce qui entraine :

$x=\dfrac{ac}{b}$

Ainsi, l'ensemble des solutions sera donné par :

$S=\left\lbrace\dfrac{ac}{b}\right\rbrace$

Remarque

Pour le cas

$c=1$ , on obtient les équations de type

$\dfrac{a}{x}=b$

D'où,

$S=\left\lbrace\dfrac{a}{b}\right\rbrace$

Exemples

Résoudre dans

$\mathbb{Q}$ les équations suivantes :

$\dfrac{7}{x}=\dfrac{4}{5}$

$\dfrac{2}{x}=3$

$\dfrac{3}{x}=\dfrac{1}{7}$

$\dfrac{5}{x}=1$

Solution

$\begin{array}{rcl}\text{a)}\ \ \dfrac{7}{x}=\dfrac{4}{5}&\Leftrightarrow&7\times 5=4x\\ \\ &\Leftrightarrow&35=4x\\ \\ &\Leftrightarrow&x=\dfrac{35}{4}\end{array}$

Ainsi,

$S=\left\lbrace\dfrac{35}{4}\right\rbrace$

$\begin{array}{rcl}\text{b)}\ \ \dfrac{2}{x}=3&\Leftrightarrow&\dfrac{2}{x}=\dfrac{3}{1}\\ \\&\Leftrightarrow&2\times 1=3x\\ \\ &\Leftrightarrow&2=3x\\ \\ &\Leftrightarrow&x=\dfrac{2}{3}\end{array}$

D'où,

$S=\left\lbrace\dfrac{2}{3}\right\rbrace$

$\begin{array}{rcl}\text{c)}\ \ \dfrac{3}{x}=\dfrac{1}{7}&\Leftrightarrow&3\times 7=x\\ \\ &\Leftrightarrow&21=x\end{array}$

Donc,

$S=\left\lbrace 21\right\rbrace$

$\begin{array}{rcl}\text{d)}\ \ \dfrac{5}{x}=1&\Leftrightarrow&\dfrac{5}{x}=\dfrac{1}{1}\\ \\&\Leftrightarrow&5\times 1=x\\ \\ &\Leftrightarrow&x=5\end{array}$

Ainsi,

$S=\left\lbrace 5\right\rbrace$