Corrigé Bac pc 1er groupe S2 S2A S4 S5 2018
Exercice 1
1.1.1 Les groupes fonctionnels et leur :
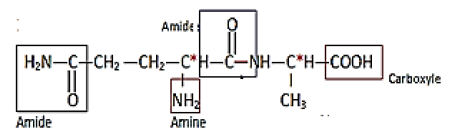
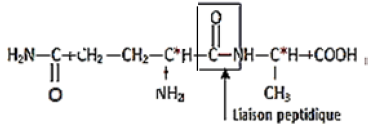
1.1.2 Liaison peptidique :
1.1.3 Les atomes de carbones asymétriques noté $C^{*}$ sont au nombre de deux (voir formule ci-dessus).
1.2.1 Définition : un acide alpha aminé est un composé organique qui possède un groupe carboxyle et un groupe amino liés au même atome de carbone tétragonal.
1.2.2 La molécule possède un atome de carbone asymétrique, elle est chirale.
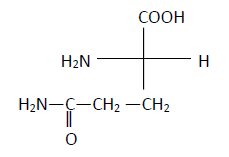
1.2.3 Représentation de Fisher de la L-glutamine :
1.3.1 Formule et nom de l'ion :
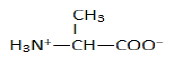
Amphion ou zwitterion
1.3.2 Réaction de l'amphion en milieu très acide et en milieu très basique et les couples associés:
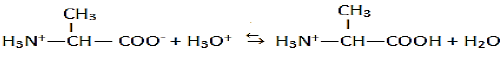
En milieu très acide
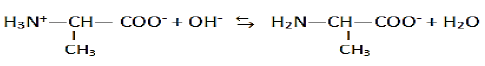
En milieu très basique
Les couples acide-base :
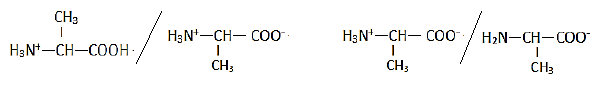
1.3.3 Diagramme de prédominance des espèces :

Exercice 2
2.1.1 Exploitation des données
$\begin{array}{rcl} [OH^{-}]&=&10^{pH-14}\\&=&10^{11.4-14}\\&=&2.51\;10^{-3}\;mol.L^{-1}\;<\;C_{b}\end{array}$
la solution d'éthanamine contient moins d'ions $OH^{-}$ qu'une solution de monobase forte de même concentration : les données prouvent que l'éthanamine est une base faible
2.1.2 Équation-bilan de la réaction avec l'eau :
$$C_{2}H_{5}NH_{2} + H_{2}O\ \leftrightarrows\ C_{2}H_{5}NH_{3}^{+} + 0H^{-}$$
2.1.3 Inventaire des espèces : $H_{3}O^{+}\;;\ 0H^{-}\;;\ C_{2}H_{5}NH_{3}^{+}\ $ et $\ C_{2}H_{5}NH_{2}$, les molécules d'eau sont ultra majoritaires.
Déterminations des concentrations molaires :
$\begin{array}{rcl} [H_{3}O^{+}]&=&10^{-pH}\\&=&10^{-11.4}\\&=&3.98\;10^{-12}\;mol.L^{-1}\end{array}$
$\begin{array}{rcl} [OH^{-}]&=&10^{pH-14}\\&=&10^{11.4-14}\\&=&2.51\;10^{-3}\;mol.L^{-1}\end{array}$
L'équation d'électroneutralité entraîne
$\begin{array}{rcl} [C_{2}H_{5}NH_{3}^{+}]&=&[OH^{-}]-[H_{3}O^{+}]\\&=&2.51\;10^{-3}\;mol.L^{-1}\end{array}$
L'équation de conservation de la matière entraîne
$\begin{array}{rcl} [C_{2}H_{5}NH_{2}]&=&C_{b}-[C_{2}H_{5}NH_{3}^{+}]\\&=&9.99\;10^{-3}\;mol.L^{-1}\end{array}$
Déduction du pKa :
$\begin{array}{rcl} pKa&=&pH-\log\left[\dfrac{[C_{2}H_{5}NH_{2}]}{[C_{2}H_{5}NH_{3}^{+}]}\right]\\ \\&=&11.4-\log\dfrac{9.99\;10^{-3}}{2.51\;10^{-3}}\\ \\&=&10.8\end{array}$
2.2.1 Schéma du dispositif du dosage :
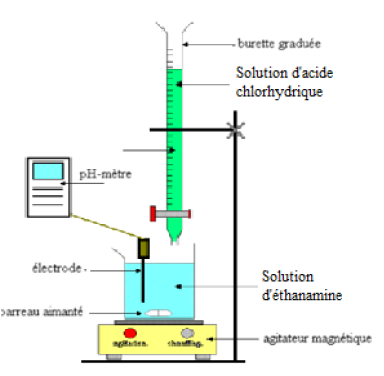
2.2.2 Équation-bilan de la réaction support du dosage :
$$[C_{2}H_{5}NH_{2}] + [H_{3}O^{+}]\ \longrightarrow\ [C_{2}H_{5}NH_{3}^{+}] + H_{2}O$$
2.2.3 Courbe $pH=f(V_{a})$ : voir ci-dessous
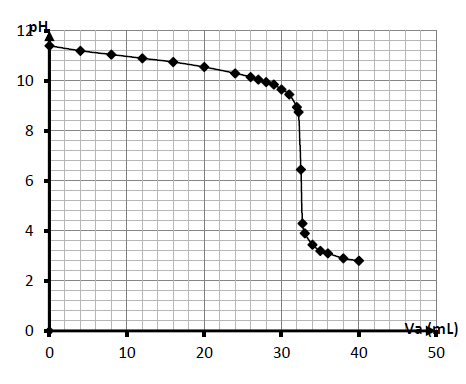
2.2.4 Le point équivalent peut être obtenu par la méthode des tangentes parallèles : $$E(V_{aE}=33\;mL\quad\text{et}\quad pH_{E}=6.3)$$
2.2.5 Équivalence :
$\begin{array}{rcl} C_{b}V_{b}'=C_{a}V_{aE}\ \Rightarrow\ C_{b}&=&\dfrac{C_{a}V_{aE}}{V_{b}'}\\ \\&=&\dfrac{0.02\times33}{50}\\ \\&=&1.32\;10^{-2}\;mol.L^{-1}\end{array}$
Aux erreurs de mesures près la valeur de la concentration molaire déduite de cette expérience est sensiblement égale à celle donnée en 2.1.
Exercice 4
4.1.1 Nom du phénomène :
Lorsque qu'on ferme l'interrupteur on a le phénomène d'auto-induction.
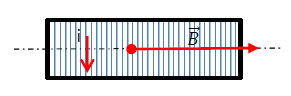
4.1.2 Schéma et vecteur champ magnétique :

4.1.3 Expression de l'inductance :
$\begin{array}{rcl} \Phi&=&NBS\quad\text{or }\ B=\dfrac{\mu_{0}Ni}{\ell}\\ \\ \Rightarrow\ \Phi&=&N\dfrac{\mu_{0}Ni}{\ell}S\\ \\&=&\dfrac{\mu_{0}N^{2}i}{\ell}S\quad\text{or }\ L=\dfrac{\Phi}{i}\\ \\\Rightarrow\ L&=&\dfrac{\mu_{0}N^{2}S}{\ell}\end{array}$
Calcul de l'inductance :
$\begin{array}{rcl} L&=&\dfrac{4\pi.10^{-7}[1280]^{2}\times 314.10^{-4}}{0.8}\\ &=&0.081\;H\\&=&81\;mH\end{array}$
$\boxed{L=81\;mH}$
4.2.1 Attribution des courbes :
Le condensateur étant chargée à $t=0$ donc $u_{C}=u_{AM}\neq 0$ :
courbe 1 $(u_{AM})\ $ et courbe 2 $(u_{DM}).$
Le phénomène expliquant la décroissance de l'amplitude de la courbe 1 : c'est la perte d'énergie par effet joule.
4.2.2 Relations : $$i=-\dfrac{dq}{dt}\quad\text{et}\quad u_{DM}=R.i$$
4.2.3 Équation différentielle :
$\begin{array}{rcl} & &u_{AM}=u_{AD}+u_{DM}\\ \\&\Rightarrow&u_{AM}=L.\dfrac{di}{dt}+R.i\quad\text{or }\ i=-\dfrac{dq}{dt}\ \text{ et }\ q=C.u_{AM}\\ \\&\Rightarrow&i=-C.\dfrac{du_{AM}}{dt}\ \text{ et }\ \dfrac{di}{dt}=-C.\dfrac{d^{2}u_{AM}}{dt^{2}}\\ \\&\Rightarrow&u_{AM}=-LC\dfrac{d^{2}u_{AM}}{dt^{2}}-RC\dfrac{du_{AM}}{dt}\\ \\&\Rightarrow&u_{AM}+LC\dfrac{d^{2}u_{AM}}{dt^{2}}+RC\dfrac{du_{AM}}{dt}=0\\ \\&\Rightarrow&\dfrac{d^{2}u_{AM}}{dt^{2}}+\dfrac{R}{L}\dfrac{du_{AM}}{dt}+\dfrac{1}{LC}u_{AM}=0\end{array}$
La pseudo-période :
graphiquement $3.5\;T=14.7\;ms\ \Rightarrow\ T=\dfrac{14.7}{3.5}=4.2\;ms$
Valeur de la capacité :
$\begin{array}{rcl} T\approx T_{0}=2\pi\sqrt{LC}&\Rightarrow&LC=\dfrac{T^{2}}{4\pi^{2}}\\ \\&\Rightarrow&C=\dfrac{T^{2}}{4\pi^{2}L}\\ \\&\Rightarrow&C=\dfrac{(4.2\;10^{-3})^{2}}{4\pi^{2}\times 0.081}\\ \\& &\quad=5.6\;10^{-6}\;F\end{array}$
$\boxed{C=5.6\;10^{-6}\;F}$
4.2.4 Expression de l'énergie électromagnétique :
$\begin{array}{rcl} & &E_{e,m}=\dfrac{1}{2}Li^{2}+\dfrac{1}{2}\dfrac{q^{2}}{C}\quad\text{or }\ q=C.u_{AM}\\ \\&\Rightarrow&u_{DM}=R.i\\ \\&\Rightarrow&E_{e,m}=\dfrac{1}{2}L\left[\dfrac{u_{DM}}{R}\right]^{2}+\dfrac{1}{2}Cu_{AM}^{2}\end{array}$
4.2.5 Valeur de $E_{e,m}(t=14.7\;ms)$
$\begin{array}{rcl} E_{e,m}=E_{\text{condensateur}}&=&\dfrac{1}{2}Cu_{AM}^{2}\\ \\&=&\dfrac{1}{2}\times 5.6\;10^{-6}\times(1.4)^{2}\\ \\&=&5.49\;10^{-6}\;J\end{array}$
$\boxed{E_{e,m}=5.49\;10^{-6}\;J}$
L'énergie dissipée :
$E_{\text{dissipée}}=|E_{e,m}(t=14.7\;ms)-E_{e,m}(t=0)|$
$\begin{array}{rcl} E_{e,m}(t=0)&=&E_{\text{condensateur}}\\ \\&=&\dfrac{1}{2}Cu_{AM}^{2}\\ \\&=&\dfrac{1}{2}\times 5.6\;10^{-6}\times(6)^{2}\\ \\&=&100.8\;10^{-6}\;J\end{array}$
$E_{\text{dissipée}}=100.8\;10^{-6}-5.49\;10^{-6}=9.53\;10^{-5}\;J$
$\boxed{E_{\text{dissipée}}=9.53\;10^{-5}\;J}$
Exercice 5
5.1.1 Composition des noyaux :
$_{26}^{59}Fe\left\lbrace\begin{array}{rcr} 26&\text{ protons}&\\33&\text{ neutrons}&\end{array}\right.\quad _{27}^{59}Co\left\lbrace\begin{array}{rcr} 27&\text{ protons}&\\32&\text{ neutrons}&\end{array}\right.$
Les deux noyaux ont en commun le même nombre de nucléons.
5.1.2 Calcul des énergies de liaison : $E_{L}=\Delta m.C^{2}$
$\begin{array}{rcl} E_{L}(_{26}^{59}Fe)&=&[26\times 1.00728+33\times 1.00867-58.9348755]\times 931.5\\&=&503.49\;MeV\end{array}$
$\begin{array}{rcl} E_{L}(_{27}^{59}Co)&=&[27\times 1.00728+32\times 1.00867-58.9331950]\times 931.5\\&=&503.76\;MeV\end{array}$
5.1.3 Comparaison de la stabilité des noyaux :
La stabilité d'un noyau est déterminée par la valeur de son énergie de liaison par nucléon. Comme les deux noyaux ont le même nombre de nucléons, la comparaison des énergies de liaison suffit pour comparer leur stabilité.
Le cobalt-59 est plus stable que le fer-59.
5.2.1 Équation de désintégration du fer :
$$_{26}^{59}Fe\ \longrightarrow\ _{27}^{59}Co + _{Z}^{A}X$$
$\left\lbrace\begin{array}{rcl} 59&=&59+A\ \Rightarrow\ A=0\ :\ \text{ loi de conservation du nombre de nucléons}\\26&=&27+Z\ \Rightarrow\ Z=-1\ :\ \text{ loi de conservation du nombre de charge}\end{array}\right.$
$$\Rightarrow\ _{Z}^{A}X=_{-1}^{\;\ 0}e$$
5.2.2 La particule émise et son origine :
La particule émise est un électron $_{-1}^{\;\ 0}e$ : l'émission d'un électron par un noyau s'explique par la transformation d'un neutron en proton : $$_{0}^{1}n\ \longrightarrow\ _{-1}^{\;\ 0}e + _{1}^{1}p$$
5.2.3.1 Définition de l'activité :
L'activité d'un échantillon radioactif est le nombre de désintégrations par unité de temps.
Expression de l'activité : $A=A_{0}\mathrm{e}^{-\lambda t}$
5.2.3.2 Calcul de la valeur de $\lambda$ :
$\begin{array}{rcrcl} A(t)=A_{0}\mathrm{e}^{-\lambda t}&\Rightarrow&A(t+10)&=&A_{0}\mathrm{e}^{-\lambda(t+10)}\\ \\&\Rightarrow&\dfrac{A(t)}{A(t+10)}&=&\dfrac{A_{0}\mathrm{e}^{-\lambda t}}{A_{0}\mathrm{e}^{-\lambda(t+10)}}\\ \\&\Rightarrow&\dfrac{A(t)}{A(t+10)}&=&\dfrac{\mathrm{e}^{-\lambda t}}{\mathrm{e}^{-\lambda(t+10)}}=1.17\\ \\&\Rightarrow&\mathrm{e}^{10.\lambda t}&=&1.17\\ \\&\Rightarrow&\lambda&=&\dfrac{\ln 1.17}{10}\\ \\& & &=&1.57\;10^{-2}\;\text{Jour}^{-1}\end{array}$
$\boxed{\lambda=1.57\;10^{-2}\;\text{Jour}^{-1}}$
La demi-vie $T$ :
$T=\dfrac{\ln 2}{\lambda}=\dfrac{\ln 2}{1.57\;10^{-2}}=44.1\;\text{jours}$
$\boxed{T=44.1\;\text{jours}}$
5.2.3.3 Calcul de $A_{0}$ :
$\begin{array}{rcl} A_{0}&=&\lambda N_{0}\\ \\&=&\lambda.\dfrac{m_{0}}{m(_{26}^{59}Fe)}\\ \\&=&\dfrac{1.57\;10^{-2}}{24\times 3600}\times\dfrac{1.5\;10^{-6}}{58.9331950\times 1.66\;10^{-27}}\\ \\&=&2.79\;10^{12}\;Bq\end{array}$
$\boxed{A_{0}=2.79\;10^{12}\;Bq}$
5.2.4 Masse de fer désintégrée à $t=10\;\text{jours}$ :
$\begin{array}{rcl} m_{\text{desint}}&=&m_{0}-m_{0}\mathrm{e}^{-\lambda t}\\&=&m_{0}(1-\mathrm{e}^{-\lambda t})\\&=&1.5(1-\mathrm{e}^{-1.57\;10^{-2}\times 10})\\&=&0.218\;mg\end{array}$
$\boxed{m_{\text{desint}}=0.218\;mg}$

Commentaires
Koné (non vérifié)
jeu, 10/19/2023 - 20:11
Permalien
J'ai besoin la correction des exercices
Koné (non vérifié)
jeu, 10/19/2023 - 20:11
Permalien
J'ai besoin la correction des exercices
Sellou Diallo (non vérifié)
ven, 06/06/2025 - 19:42
Permalien
Besoin des corrections des exercices des BAC
Brahim tall (non vérifié)
mar, 02/10/2026 - 22:58
Permalien
Demande d acces a des correction d exercices bac
Ajouter un commentaire