Série d'exercices : Force et champ électrostatiques - 1er s
Classe:
Première
Exercice 1 : pendule et force électrostatique
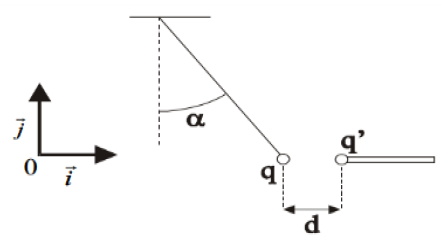
Une bille de masse $m=20\,g$ est suspendu à un fil de longueur $l=10\,cm.$
La bille porte une charge électrique $q$ que l'on souhaite déterminer.
En approchant horizontalement une tige isolante qui porte à son extrémité une charge $q'=+10^{-6}C$, la bille est attirée par la tige et le fil fait un angle $\alpha=20^{\circ}$ par rapport à la verticale.
Les charges $q$ et $q'$ sont situés à une distance $d=2\,cm.$
1) Faire le bilan des forces qui s'exercent sur la bille et les représenter
2) Écrire la condition d'équilibre
3) Déterminer l'intensité de la force électrostatique.
4) En déduire la charge $q$ portée par la bille. $\left(k=1/\left(4\pi\varepsilon_{0}\right)=9.0\cdot 10^{9}N\cdot m^{2}\cdot C^{-2}\right)$
Exercice 2
On place aux points $A$ et $B$ deux boules métalliques identiques $\left(B_{1}\right)$ et $\left(B_{2}\right)$ supposées ponctuelles.
La distance entre $A$ et $B$ est égale à $2a.$
La boule $\left(B_{1}\right)$ porte la charge $-q$ et la boule $\left(B_{2}\right)$ porte la charge $+q$ $(q>0).$
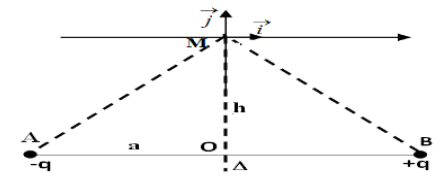
On note $O$ milieu du segment $[AB]$ et $(\Delta)$ la médiatrice de $[AB]$ contenue dans le plan de la figure.
Soit $M$ un point de $(\Delta)$ distant de $h$ du point $O.$ (figure 1)
1.1. Définir la ligne de champ.
Représenter le spectre électrique des deux charges placées en $A$ et $B.$
1.2. Représenter les vecteurs champs électriques $\overrightarrow{E}_{A}$ et $\overrightarrow{E}_{B}$ créés respectivement par $B_{1}$ et $B_{2}$ au point $M.$
1.3. Exprimer la valeur de $E_{A}$ et de $E_{B}$ en fonction de $K$, $q$, $a$ et $h.$
Montrer que $E_{A}=E_{B}\cdot K=9\cdot 10^{9}\quad u.s.i$
2. On notera $\overrightarrow{E}_{M}$ le champ électrique créé par les deux boules $\left(B_{1}\right)$ et $\left(B_{2}\right)$ au point $M.$
2.1. Déterminer les coordonnées $E_{Mx}$ et $E_{My}$ du vecteur $\overrightarrow{E}_{M}$ dans le repère orthonormé $(M\;,\ \vec{i}\;,\ \vec{j})$ en fonction de $K$, $q$, $a$ et $h.$
2.2. Montrer que :
$$\overrightarrow{E}_{M}=-\dfrac{2K|q|\cos\alpha}{\left(a^{2}+h^{2}\right)}\overrightarrow{i}\;,\text{ avec }\cos\alpha=\dfrac{a}{\sqrt{a^{2}+h^{2}}}$$
2.3. Déduire la valeur de $\overrightarrow{E}_{M}$ au point $O.$
On donne $a=10\,cm\;,\ h=17.33\,cm\text{ et }q=0.3\mu C.$
Exercice 3
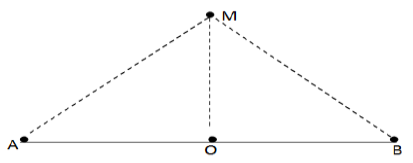
Deux charges électriques ponctuelles sont placées aux points $A$ et $B$ distants de $10\,cm.$
La charge placée en $A$ vaut $q_{A}=-3\cdot 10^{-9}C$ celle placée en $B$ vaut $q_{B}=4\cdot10^{-9} C.$
1. Énoncer la loi de Coulomb.
2.1. Déterminer les caractéristiques de la force exercée par $A$ sur $B$ et la force exercée par $B$ sur $A.$
2.2. Représenter $\overrightarrow{F}_{B/A}$ et $\overrightarrow{F}_{A/B}$
3. Déterminer les caractéristiques du vecteur champ électrostatique $\overrightarrow{E}$ créé par ces deux charges électriques en ces deux cas, puis les représenter.
3.1. Au milieu $O$ de segment $AB.$
3.2. En un point $M$ de la médiatrice de $AB$, situé à $5\,cm$ de $O.$
4. Quelles sont les caractéristiques d'un champ électrique uniforme (donner un schéma de spectre de champ)
Exercice 4
Trois pendules électrostatiques sont formés de trois petites sphères identiques $A$, $B$ et $C$, supposées ponctuelles, de même masse $m=10.0\,g$, suspendues par des fils de masses négligeables à un support horizontal de telle façon que leurs points d'attache respectifs $A'$, $B'$ et ce sont régulièrement espacés : $A'B'=B'C'$ (voir Figure ci-dessous).
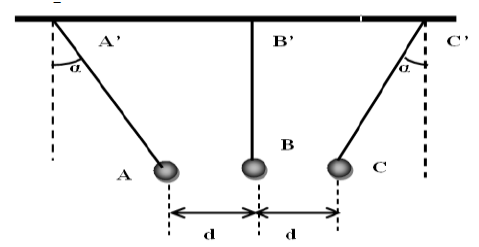
Les deux fils supportant les sphères $A$ et $C$ sont de même longueur $l$, égale à $25.0\,cm$, et forment tous les deux un angle $\alpha$ avec la verticale.
Le fil supportant la sphère $B$ est vertical et d'une longueur $l'$ telle que les centres de $A$, $B$ et $C$ sont alignés dans un même plan horizontal.
Les sphères $A$ et $C$ portent chacune la même charge : $q=+200\,nC$
La sphère $B$ porte une charge $q'$ de valeur double de celle de $q.$
Données :
Distance $d$ entre les centres de $A$ et $B$ $($égale à la distance entre les centres de $B$ et $C)$ : $d=10.0\,cm.$
Accélération de la pesanteur : $g=9.81\,m\cdot s^{-2}.$
Interaction de Coulomb : $k=9.00\cdot10\,u\ S.I$
Interaction de Newton : $G=6.67\cdot10^{-11}u\ S.I$
On néglige les actions de l'air, ainsi que les interactions gravitationnelles entre les sphères.
1. Quel est le signe de $q'$ ?
Justifier.
2. On s'intéresse à l'équilibre de $A.$
2.1. Faire le bilan des forces qui s'exercent sur $A$, sans faire intervenir, pour simplifier, l'action de $C.$
2.2. Représenter ces forces sur un schéma, sans souci d'échelle mais en respectant leurs directions, leurs sens et leurs points d'application.
2.3. Énoncer la condition d'équilibre de $A.$
2.4. En déduire la valeur de l'angle $\alpha.$
2.5. Déterminer les valeurs des forces qui s'exercent sur $A.$
3. On s'intéresse à l'équilibre de $B.$
3.1. Faire le bilan des forces qui s'exercent sur $B.$
3.2. Représenter ces forces sur un schéma, sans souci d'échelle mais en respectant leurs directions, leurs sens et leurs points d'application.
3.3. Déterminer les valeurs des forces qui s'exercent sur $B.$
Exercice 5
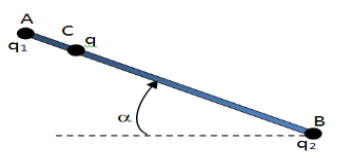
Une tige isolante $AB$ $(AB=20\,cm)$ est inclinée d'un angle $\alpha=30^{\circ}$ avec l'horizontale.
1. On fixe en $A$ une charge $q_{1}=-10\,nC$, en $B$ une charge $q_{2}=10\,nC.$
Déterminer les caractéristiques du vecteur champ électrostatique au point $C$ situé sur la tige $AB$ à $5\,cm$ de $A.$
2. Une petite sphère $(S)$ portant une charge $q=30\,nC$, de masse $m$, peut coulisser sans frottement sur la tige $AB$, elle s'immobilise en $C.$
a) Faire le bilan des forces qui s'exercent sur la sphère $(S)$ ; les représenter.
b) En appliquant la condition d'équilibre de la sphère, calculer la masse $m$ et la valeur de la réaction de la tige.
On donne $g=10\,N\cdot Kg^{-1}.$
3. En maintenant la tige $AB$ horizontalement, la sphère reste-t-elle immobile ?
Si non dans quel sens va-t-elle se déplacer ?
Exercice 6
On donne la constante électrostatique $K=9\cdot10^{9}\ u.s.i.$
Le schéma de la figure 1 représente deux pendules électrostatiques, de même longueur $l=20\,cm$, portant, respectivement, à leurs extrémités libres deux boules supposées ponctuelles $A$ et $B$ de même masse et de charges respectives $q_{A}=-q_{B}=2\mu C.$

Lorsqu'on rapproche les pendules l'un de l'autre, ils prennent la position d'équilibre indiquée sur le schéma de la figure
À l'équilibre, chacun des deux pendules fait un angle $\alpha$ très petit avec $\sin\alpha=0.1.$
La distance séparant les deux points d'attache $O$ et $O'$ des deux pendules est $OO'=14\,cm.$
1. Calculer la distance $AB$ à l'équilibre.
2.1. Représenter toutes les forces exercées sur les boules $A$ et $B$
2.2. Déterminer la valeur de la force de l'interaction électrique existant entre les boules $A$ et $B.$
Exercice 7
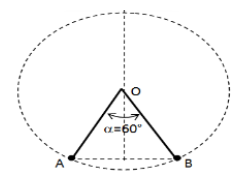
Deux points $A$ et $B$ sont situés sur la circonférence d'un cercle de centre $O$ et de rayon $R=6\,cm.$
En $A$ et $B$ on place respectivement deux boules ponctuelles chargées de même charge $q_{A}=q_{B}=2\cdot10^{-7}C$ et de masses négligeables.
1. Représenter les forces électriques $\overrightarrow{F}_{A/B}$ et $\overrightarrow{F}_{B/A}$ qui constituent l'interaction électrique existant entre $q_{A}$ et $q_{B}.$
Donner les caractéristiques de $\overrightarrow{F}_{A/B}$
2.1. Représenter, au point $O$, les vecteurs champs électrostatiques de $\overrightarrow{E}_{A}$ et $\overrightarrow{E}_{B}$ créés respectivement par les charges $q_{A}$ et $q_{B}.$
Calculer la valeur de $\overrightarrow{E}_{A}$
2.2. Déterminer les caractéristiques du vecteur champ électrostatique $\overrightarrow{E}_{O}=\overrightarrow{E}_{A}+\overrightarrow{E}_{B}$ créé par l'ensemble des deux charges au point $O.$
3. Au point $O$, on place un corps ponctuel $(C)$ de masse $m$ qui porte une charge de valeur absolue $|Q_{0}|=2\cdot10^{-8}C$, il prend une position d'équilibre stable.
3.1. Représenter la force $\overrightarrow{F}$ exercée par $q_{A}$ et $q_{B}$ sur la charge $Q_{0}.$
Quel est le signe de $Q_{0}$ ?
Justifier la réponse.
3.2 Écrire la condition d'équilibre du corps ponctuel $(C).$
Calculer la masse $m$ du corps
Exercice 8
Une sphère de centre $S$ est attachée au point $O$ par un fil isolant de masse négligeable et de longueur $l=40\,cm.$
La sphère, de masse $m=2\cdot10^{-2}kg$, porte une charge $q.$
$$g=10\,N\cdot kg^{-1}$$
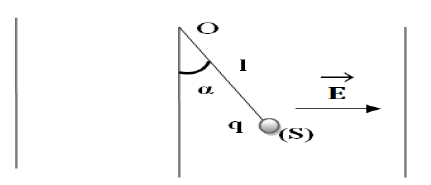
1. On la soumet à un champ électrique uniforme $E$, horizontal, orienté comme indique la figure.
Le fil s'incline alors d'un angle $\alpha=10^{\circ}$ par à rapport à la verticale.
En déduire la valeur de la charge $q.$
Intensité du champ électrostatique $E=10^{3}V\cdot m^{-1}$
2. On superpose au champ électrostatique précédent, un autre champ électrostatique uniforme $E'$ vertical.
Quels doivent être le sens et l'intensité du champ $E'$ pour que le fil s'incline sur la verticale d'un angle $\alpha=20^{\circ}$
3. Quelle serait l'inclinaison $\alpha'$ si l'on changeait le sens de $E'$ sans modifier son intensité
Exercice 9
Deux petites sphères métalliques et identiques sont fixées aux extrémités $A$ et $B$ d'une barre.
On a : $AO=OB=l$
Les sphères sont chargées et portent respectivement les charges $q$ et $-q.$
On introduit ce dispositif entre deux plaques parallèles.
Lorsque celles-ci sont branchées à la terre, la barre $AOB$ est parallèle aux plaques, et le fil n'est pas tordu.
Lorsque les plaques sont branchées à la terre, la barre $AOB$ est parallèle aux plaques, et le fil n'est pas tordu.
Lorsque les plaques sont branchées à un générateur haute tension, il existe un champ électrostatique uniforme $\overrightarrow{E}$ perpendiculaire aux plaques.
La barre $AOB$ fait alors un angle $\alpha$ avec la direction précédente et reste horizontale
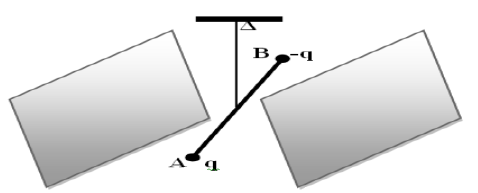
1. Calculer en fonction de $l$, $\alpha$, $q$ et $E$ le moment des forces électrostatiques par rapport à l'axe de rotation du dispositif.
2. Calculer le moment du poids du système par rapport à l'axe de rotation.
3. Le dispositif étant en équilibre, le fil de torsion exerce des actions mécaniques dont le moment par rapport à l'axe de rotation est proportionnel à l'angle de rotation $\alpha$ :
$|M_{\Delta}|=C\alpha$ Avec $C=13.5\cdot10^{-7}N\cdot m\cdot rad^{-1}.$
Calculer $q$ sachant que : $E=272\,V\cdot m^{-1}$ ; $l=15\,cm$ ; $\alpha=\dfrac{\pi}{6}.$
Exercice 10
En deux points $A$ et $B$ tels que $OA=OB=d$, sont placées deux charges ponctuelles égales $q$ et de même signe.
On se propose de déterminer le champ électrique crée par ces deux charges en un point $M$ tel que $OM=x.$
Établir, en fonction de $x$, $d$ et $q$ ; l'expression du champ électrique crée par les deux charges au point $M$ dans chacun des cas représentés sur les schémas suivants :
1) Le point $M$ se trouve sur le segment $[AB]$ entre les points $O$ et $B$ :
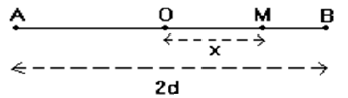
2) Le point $M$ se trouve dans l'alignement de $AB$ à l'extérieur du segment $[AB]$ du côté du point $B$ :

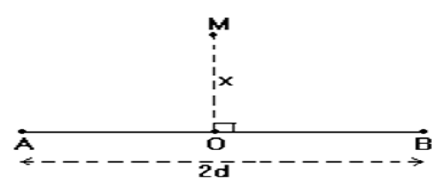
3) Le point $M$ est situé sur la médiatrice du segment $[AB]$ :
Exercice 11
Une charge ponctuelle $Q=-40\,nC$ est placée au sommet $A$ d'un carré $ABCD$ de $2.0\,cm$ de côté
1. Déterminer les caractéristiques (valeur, direction et sens) des champs électriques $\overrightarrow{E}_{B}$ et $\overrightarrow{E}_{C}$ créés par cette
charge aux points $B$ et $C.$
2. Représenter ces champs
3. Représenter quelques lignes de champs autour du point $A.$
4. On place une charge ponctuelle $q=-10\,nC$ au point $C.$
4.1. Déterminer les caractéristiques (valeur, direction et sens) de la force électrique s'exerçant sur cette charge.
4.2. Représenter cette force
4.3. Représenter, à la même échelle, la force électrique qui s'exerce sur la charge $Q.$


Commentaires
Imad Msaadi (non vérifié)
dim, 03/14/2021 - 20:19
Permalien
correction de l'exercices électrostatique
Jean_Berchmans_... (non vérifié)
sam, 09/25/2021 - 08:47
Permalien
AIDER MON ENFANT EN COURS DE PHYSISQUE
Sidiahmedaly (non vérifié)
jeu, 03/10/2022 - 21:08
Permalien
Correction calorimetr
Hanane (non vérifié)
mer, 02/08/2023 - 19:38
Permalien
Reponse
Saif (non vérifié)
mar, 11/14/2023 - 17:20
Permalien
Résoudre un problème de physique
Saif (non vérifié)
mar, 11/14/2023 - 17:20
Permalien
Résoudre un problème de physique
Zafimena (non vérifié)
lun, 03/10/2025 - 08:36
Permalien
Mathématiques
Siman (non vérifié)
mar, 03/11/2025 - 01:33
Permalien
Comprendre mieu la phisique
Mark (non vérifié)
dim, 03/21/2021 - 12:29
Permalien
Appréciait
Mark (non vérifié)
dim, 03/21/2021 - 12:29
Permalien
Appréciait
Fatima Dia (non vérifié)
ven, 04/09/2021 - 12:12
Permalien
Correction de la serie
Dered (non vérifié)
dim, 06/27/2021 - 22:25
Permalien
Ggyyy
Malick cisse (non vérifié)
dim, 06/27/2021 - 22:28
Permalien
Voir
DJE BI (non vérifié)
mer, 04/14/2021 - 15:42
Permalien
Apprendre quelques notions sur la science
Anonyme (non vérifié)
mer, 04/14/2021 - 15:43
Permalien
Y'a des bons exercices qui
Khota fall (non vérifié)
mar, 05/18/2021 - 08:37
Permalien
D'avoir des bonnes note en classe
Mame Abdoulaye Niass (non vérifié)
mer, 04/27/2022 - 01:06
Permalien
Réussie
Mouhamadou Mokh... (non vérifié)
lun, 06/07/2021 - 22:09
Permalien
Le savoir
Thiané (non vérifié)
jeu, 06/17/2021 - 21:08
Permalien
Comment calculer l'angle d'un
Thiané ngom (non vérifié)
sam, 06/19/2021 - 02:23
Permalien
Force
Abibou Brym (non vérifié)
sam, 11/27/2021 - 14:13
Permalien
Corrigé des exercices
Khadre Leye (non vérifié)
dim, 05/15/2022 - 19:03
Permalien
Trouver des exercices corrigés
Iheb saada (non vérifié)
sam, 11/12/2022 - 23:36
Permalien
Exercices champ et potentiel electrostatique
Faustin (non vérifié)
jeu, 10/06/2022 - 03:26
Permalien
Remarque
abdeljalil (non vérifié)
jeu, 02/02/2023 - 18:01
Permalien
correction de l'exercice de champ electrostatique
Anonyme (non vérifié)
ven, 02/17/2023 - 14:21
Permalien
correction des exercices svp,
Anonyme (non vérifié)
ven, 02/17/2023 - 14:21
Permalien
correction des exercices svp,
Tézia (non vérifié)
ven, 01/12/2024 - 05:59
Permalien
Ça va aller
Asensow (non vérifié)
mar, 01/30/2024 - 01:53
Permalien
Merci infiniment
Ajouter un commentaire