Vous êtes ici

Corrigé devoir n° 1 maths - 5e

Classe:

Cinquième

Exercice 1

Complétons, si possible, les phrases ci-dessous en utilisant les expressions : "complémentaires, supplémentaires, opposés par le sommet, alternes-internes, correspondants".

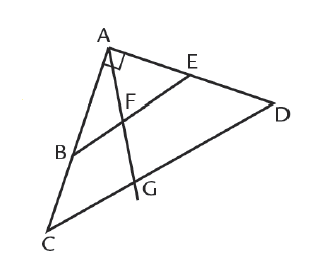
1) $\widehat{AFB}\ $ et $\ \widehat{AFE}$ sont des angles supplémentaires.

2) $\widehat{ABE}\ $ et $\ \widehat{ACD}$ sont des angles correspondants.

3) $\widehat{AFE}\ $ et $\ \widehat{BFG}$ sont des angles opposés par le sommet.

4) $\widehat{BAF}\ $ et $\ \widehat{FAE}$ sont des angles complémentaires.

5) $\widehat{EFG}\ $ et $\ \widehat{FGC}$ sont des angles alternes-internes.

Exercice 2

On considère la figure ci-dessous.

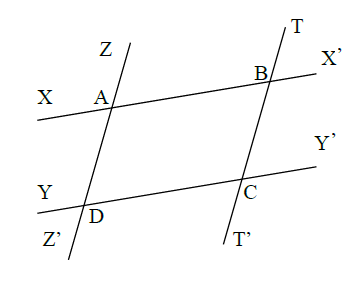
1) Nommons les angles du sommet $A.$

On peut citer :

$$\widehat{XAZ}\;;\ \widehat{XAZ'}\;;\ \widehat{Z'AX'}\;;\ \widehat{ZAX'}\;;\ \widehat{XAX'}\;;\ \widehat{ZAZ'}$$

2) Sur la figure on peut compter $24$ angles.

Au niveau de chaque sommet, on a $6$ angles. Donc, pour les $4$ sommets on obtient : $4\times 6=24$ angles.

D'où, on peut compter $24$ angles sur la figure.

3) Citons deux angles : Alternes internes - Alternes externes - correspondants - opposés par le sommet - intérieurs - extérieurs - adjacents supplémentaires.

On a :

$\widehat{X'BC}\ $ et $\ \widehat{DCB}$ sont deux angles alternes-internes.

$\widehat{XAZ}\ $ et $\ \widehat{Z'DC}$ sont deux angles alternes-externes.

$\widehat{ZAB}\ $ et $\ \widehat{ADC}$ sont deux angles correspondants.

$\widehat{BCY'}\ $ et $\ \widehat{DCT'}$ sont deux angles opposés par le sommet $C.$

$\widehat{ABC}\ $ et $\ \widehat{ADC}$ sont deux angles intérieurs au quadrilatère $ABCD.$

$\widehat{XAZ}\ $ et $\ \widehat{YDZ'}$ sont deux angles extérieurs au quadrilatère $ABCD.$

$\widehat{XAZ}\ $ et $\ \widehat{ZAB}$ sont deux angles adjacents supplémentaires.

Exercice 3

1) Construisons un triangle $ABC$ tel que :

$$AB=4\;cm\;;\ BC=3\;cm\ \text{ et }\ AC=2\;cm$$

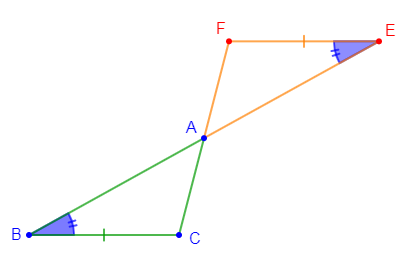
2) Construisons le triangle $AEF$ symétrique du triangle $ABC$ par rapport au point $A.$

3) Le segment $[BC]$ a la même longueur que $[EF]$

4) L'angle $\widehat{B}$ de la figure a la même mesure que l'angle $\widehat{E}$

Rappel : le symétrique d'un triangle est un triangle de même nature.

Exercice 4

1) Les nombres $1\,409\ $ et $\ 1\,009$ sont premiers.

En effet, $1\,409\ $ et $\ 1\,009$ ne sont divisibles que par $1$ et par eux-mêmes donc, ce sont des nombres premiers.

2) Déterminons le $PGCD$ et le $PPCM$ des nombres $1\,420\ $ et $\ 2\,772$

En décomposant $1\,420\ $ et $\ 2\,772$ en produits de facteurs premiers, on obtient :

$\begin{array}{r|l} 1420&2\\710&2\\355&5\\71&71\\1&\end{array}$ Donc, $1\,420=2^{2}\times 5\times 71$

$\begin{array}{r|l} 2772&2\\1386&2\\693&3\\231&3\\77&7\\11&11\\1&\end{array}$ Donc, $2\,772=2^{2}\times 3^{2}\times 7\times 11$

Par suite,

$\begin{array}{rcl} PGCD(1\,420\;;\ 2\,772)&=&2^{2}\\&=&4\end{array}$

$\begin{array}{rcl} PPCM(1\,420\;;\ 2\,772)&=&2^{2}\times 5\times 71\times 3^{2}\times 7\times 11 \\&=&984\,060\end{array}$

D'où, $\boxed{PGCD(1\,420\;;\ 2\,772)=4\ \text{ et }\ PPCM(1\,420\;;\ 2\,772)=984\,060}$

a) Écrivons alors la liste des diviseurs communs de ces deux nombres

$$1\ -\ 2\ -\ 4$$

Exercice 5

1) Écrivons l'ensemble $D$ des diviseurs de $30.$

En décomposant $30$ en produits de facteurs premiers, on obtient :

$30=1\times 2\times 3\times 5$

Donc, $D=\{1\;;\ 2\;;\ 3\;;\ 5\;;\ 6\;;\ 10\;;\ 15\;;\ 30\}$

2) Écrivons l'ensemble $E$ des diviseurs de $12.$

La décomposition de $12$ en produits de facteurs premiers donne :

$12=1\times 2^{2}\times 3$

Par suite, $E=\{1\;;\ 2\;;\ 3\;;\ 4\;;\ 6\;;\ 12\}$

3) Les diviseurs communs de $30$ et de $12$ sont donnés par :

$$D\cap E=\{1\;;\ 2\;;\ 3\;;\ 6\}$$

4) $6$ est le plus grand diviseur commun de $30\ $ et $\ 12$

Auteur:

Diny Faye

Commentaires

Anonyme (non vérifié)

lun, 10/18/2021 - 14:45