Solution des exercices : Les vecteurs 3e
Classe:
Troisième
Exercice 1
Soit $L\;,\ O\;,\ U$ trois points non alignés du plan et $S$ le milieu du segment $[OU].$
1) Construisons le point $I$ tel que : $\overrightarrow{LI}=\overrightarrow{LO}+\overrightarrow{LU}$
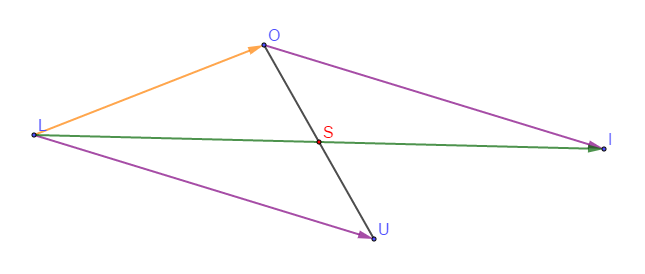
2) Démontrons que : $\overrightarrow{LO}+\overrightarrow{LU}=2\overrightarrow{LS}$
1e méthode :
Calculons : $\overrightarrow{LO}+\overrightarrow{LU}$
Décomposons les vecteurs $\overrightarrow{LO}\ $ et $\ \overrightarrow{LU}$ en utilisant le point $S$, suivant la relation de Chasles. Ce qui donne :
$\overrightarrow{LO}=\overrightarrow{LS}+\overrightarrow{SO}$
$\overrightarrow{LU}=\overrightarrow{LS}+\overrightarrow{SU}$
Donc, en remplaçant, $\overrightarrow{LO}\ $ et $\ \overrightarrow{LU}$ par leur expression, on obtient :
$\begin{array}{rcl}\overrightarrow{LO}+\overrightarrow{LU}&=&\left(\overrightarrow{LS}+\overrightarrow{SO}\right)+\left(\overrightarrow{LS}+\overrightarrow{SU}\right)\\\\&=&\overrightarrow{LS}+\overrightarrow{SO}+\overrightarrow{LS}+\overrightarrow{SU}\\\\&=&\overrightarrow{LS}+\overrightarrow{LS}+\overrightarrow{SO}+\overrightarrow{SU}\\\\&=&2\overrightarrow{LS}+\overrightarrow{SO}+\overrightarrow{SU}\end{array}$
Mais comme $S$ est le milieu du segment $[OU]$ alors, on a : $\overrightarrow{SO}+\overrightarrow{SU}=\vec{0}$
D'où, $\boxed{\overrightarrow{LO}+\overrightarrow{LU}=2\overrightarrow{LS}}$
2e méthode :
En effet, comme $S$ est le milieu du segment $[OU]$ alors, on a :
$$\overrightarrow{SO}+\overrightarrow{SU}=\vec{0}$$
Décomposons les vecteurs $\overrightarrow{SO}\ $ et $\ \overrightarrow{SU}$ en utilisant le point $L$, suivant la relation de Chasles. Ce qui donne alors :
$\overrightarrow{SO}=\overrightarrow{SL}+\overrightarrow{LO}$
$\overrightarrow{SU}=\overrightarrow{SL}+\overrightarrow{LU}$
Par suite, en remplaçant $\overrightarrow{SO}\ $ et $\ \overrightarrow{SU}$ par leur expression, on obtient :
$\begin{array}{rcl}\overrightarrow{SO}+\overrightarrow{SU}=\vec{0}&\Leftrightarrow&\left(\overrightarrow{SL}+\overrightarrow{LO}\right)+\left(\overrightarrow{SL}+\overrightarrow{LU}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{SL}+\overrightarrow{LO}+\overrightarrow{SL}+\overrightarrow{LU}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{LO}+\overrightarrow{LU}+2\overrightarrow{SL}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{LO}+\overrightarrow{LU}=-2\overrightarrow{SL}\\\\&\Leftrightarrow&\overrightarrow{LO}+\overrightarrow{LU}=2\overrightarrow{LS}\end{array}$
D'où, $\boxed{\overrightarrow{LO}+\overrightarrow{LU}=2\overrightarrow{LS}}$
Exercice 2
Soit $ABCD$ un parallélogramme de centre $O$ et $M$ un point quelconque du plan.
1) Construisons un point $N$ tel que $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MN}$
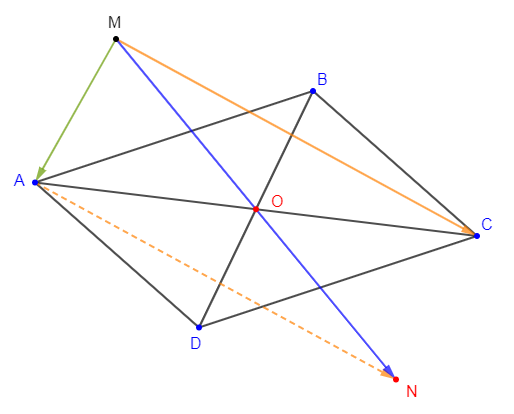
2) Montrons que $\overrightarrow{MN}=2\overrightarrow{MO}$
D'après la question $1)$, on a : $\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{MC}$
Or, on sait que $ABCD$ est un parallélogramme de centre $O.$
Donc, $O$ est milieu de la diagonale $[AC].$
Ainsi, d'après une propriété du cours, pour tout point $M$ du plan, on a :
$$\overrightarrow{MA}+\overrightarrow{MC}=2\overrightarrow{MO}$$
D'où, $\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{MC}=2\overrightarrow{MO}$
Par conséquent, $\boxed{\overrightarrow{MN}=2\overrightarrow{MO}}$
3) Montrons que $\overrightarrow{MB}+\overrightarrow{MD}=\overrightarrow{MN}$
En effet, comme $ABCD$ est un parallélogramme de centre $O$ alors, la diagonale $[BD]$ a pour milieu le point $O.$
Ainsi, d'après une propriété du cours, pour tout point $M$ du plan, on a :
$$\overrightarrow{MB}+\overrightarrow{MD}=2\overrightarrow{MO}$$
Or, d'après le résultat de la question $2)$, on a : $\overrightarrow{MN}=2\overrightarrow{MO}$
D'où, $\boxed{\overrightarrow{MB}+\overrightarrow{MD}=\overrightarrow{MN}}$
4) Déduisons que $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}$
D'après le résultat des questions précédentes, on a :
$\overrightarrow{MA}+\overrightarrow{MC}=2\overrightarrow{MO}$
$\overrightarrow{MB}+\overrightarrow{MD}=2\overrightarrow{MO}.$
Donc, en remplaçant $\overrightarrow{MA}+\overrightarrow{MC}\ $ et $\ \overrightarrow{MB}+\overrightarrow{MD}$ par leur expression, on obtient :
$\begin{array}{rcl} \overrightarrow{MA}+\overrightarrow{MC}+\overrightarrow{MB}+\overrightarrow{MD}&=&2\overrightarrow{MO}+2\overrightarrow{MO}\\\\ &=&4\overrightarrow{MO}\end{array}$
D'où, $\boxed{\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}}$
Exercice 3
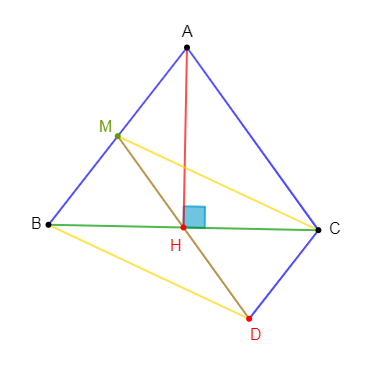
Soit un parallélogramme $ABCD$ et $M$ un point quelconque sur la diagonale $[BD].$
1) Construisons les points $E$ et $F$ vérifiant : $$\overrightarrow{AM}+\overrightarrow{AD}=\overrightarrow{AE}\quad\text{et}\quad\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{AF}$$
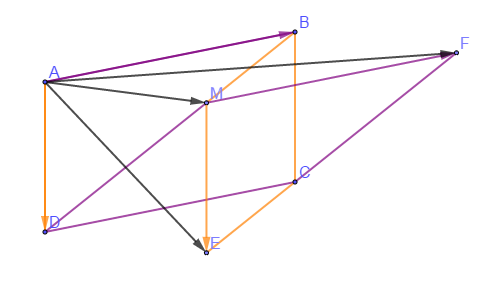
2) Citons deux vecteurs égaux à $\overrightarrow{AD}.$
$ABCD$ étant un parallélogramme alors, on a :
$$\overrightarrow{AD}=\overrightarrow{BC}$$
De plus, d'après la question $1)$, on a : $\overrightarrow{AM}+\overrightarrow{AD}=\overrightarrow{AE}$
Ainsi, $\overrightarrow{AD}=\overrightarrow{AE}-\overrightarrow{AM}$
Or, on sait que : $-\overrightarrow{AM}=\overrightarrow{MA}$
Ce qui donne alors, $\overrightarrow{AD}=\overrightarrow{MA}+\overrightarrow{AE}$
D'où, en appliquant la relation de Chasles, on obtient :
$$\overrightarrow{AD}=\overrightarrow{ME}$$
Ainsi, $\overrightarrow{BC}\ $ et $\ \overrightarrow{ME}$ sont deux vecteurs égaux à $\overrightarrow{AD}.$
En déduisons que $MBCE$ est un parallélogramme.
On a : $\left\{\begin{array}{rcl}\overrightarrow{AD}&=&\overrightarrow{BC} \\\\ \overrightarrow{AD}&=&\overrightarrow{ME}\end{array}\right.\quad\text{donc, }\overrightarrow{BC}=\overrightarrow{ME}$
D'où, $MBCE$ est un parallélogramme.
3) Citons deux vecteurs égaux à $\overrightarrow{AB}.$
Comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{AB}=\overrightarrow{DC}$$
Aussi, d'après la question $1)$, on a : $\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{AF}$
Donc, $\overrightarrow{AB}=\overrightarrow{AF}-\overrightarrow{AM}$ or, $-\overrightarrow{AM}=\overrightarrow{MA}$
Par suite, $\overrightarrow{AB}=\overrightarrow{MA}+\overrightarrow{AF}$
D'où, en utilisant la relation de Chasles, on obtient :
$$\overrightarrow{AB}=\overrightarrow{MF}$$
Ainsi, $\overrightarrow{DC}\ $ et $\ \overrightarrow{MF}$ sont deux vecteurs égaux à $\overrightarrow{AB}.$
Comme $\left\{\begin{array}{rcl}\overrightarrow{AB}&=&\overrightarrow{DC} \\\\ \overrightarrow{AB}&=&\overrightarrow{MF}\end{array}\right.\quad\text{alors,}\ \overrightarrow{DC}=\overrightarrow{MF}$
Donc, le quadrilatère $MDCF$ est un parallélogramme.
4) Démontrons, en utilisant les questions précédentes, que les points $E\;,\ C\ $ et $\ F$ sont alignés.
En effet, comme $M\in[BD]$ alors, les vecteurs $\overrightarrow{DM}\ $ et $\ \overrightarrow{MB}$ sont colinéaires.
Ce qui signifie qu'il existe un nombre réel $k>0$ tel que : $$\overrightarrow{DM}=k.\overrightarrow{MB}\qquad(*)$$
Or, d'après la question $2)$, on a : $MBCE$ est un parallélogramme.
Donc, $\overrightarrow{MB}=\overrightarrow{EC}$
De même, d'après la question $3)$, on a : $MDCF$ est un parallélogramme.
Donc, $\overrightarrow{DM}=\overrightarrow{CF}$
Ainsi, en remplaçant $\overrightarrow{DM}\ $ et $\ \overrightarrow{MB}$ respectivement par $\overrightarrow{CF}\ $ et $\ \overrightarrow{EC}$ dans la relation $(*)$ on obtient : $$\overrightarrow{CF}=k.\overrightarrow{EC}$$
Ce qui permet alors de dire que $\overrightarrow{CF}\ $ et $\ \overrightarrow{EC}$ sont colinéaires.
D'où, $E\;,\ C\ $ et $\ F$ sont alignés.
Exercice 4
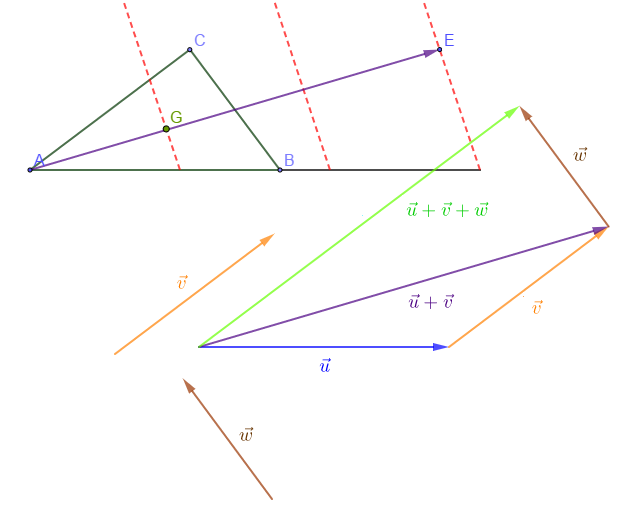
1) Construisons le triangle $ABC$ tel que
$AB=5\;cm\;;\ AC=4\;cm$ et $BC=3\;cm.$
2) On pose $\vec{u}=\overrightarrow{AB}\;;\ \vec{v}=\overrightarrow{AC}.$
Construisons $\vec{u}+\vec{v}$
3) Plaçons le point $E$ tel que $\overrightarrow{AE}=\vec{u}+\vec{v}$ et divisons le segment $[AE]$ en trois parties égales.
4) On pose $\vec{w}=\overrightarrow{BC}$.
Construisons $\vec{u}+\vec{v}+\vec{w}$

5) Soit $G$ un point du plan tel que $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}.$
Démontrons que $\overrightarrow{AG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}$
Suivant la relation de Chasles, décomposons les vecteurs $\overrightarrow{GB}\ $ et $\ \overrightarrow{GC}$ en utilisant le point $A.$ Ce qui donne alors :
$\overrightarrow{GB}=\overrightarrow{GA}+\overrightarrow{AB}$
$\overrightarrow{GC}=\overrightarrow{GA}+\overrightarrow{AC}$
Ensuite, en remplaçant $\overrightarrow{GB}\ $ et $\ \overrightarrow{GC}$ par leur expression, on obtient :
$\begin{array}{rcl}\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}&\Leftrightarrow&\overrightarrow{GA}+\left(\overrightarrow{GA}+\overrightarrow{AB}\right)+\left(\overrightarrow{GA}+\overrightarrow{AC}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{GA}+\overrightarrow{GA}+\overrightarrow{AB}+\overrightarrow{GA}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{GA}+\overrightarrow{AB}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{GA}=-\overrightarrow{AB}-\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{GA}=-\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}\\\\&\Leftrightarrow&-\overrightarrow{GA}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}\\\\&\Leftrightarrow&\overrightarrow{AG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}\end{array}$
D'où, $\boxed{\overrightarrow{AG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}}$
Exercice 5
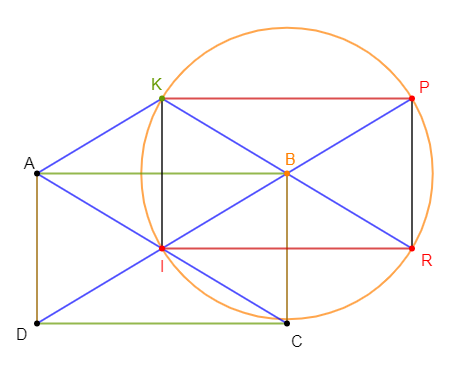
1) a) Traçons un rectangle $ABCD$ de centre $I.$
Construisons le point $K$ tel que $\overrightarrow{IK}=\overrightarrow{IA}+\overrightarrow{IB}$
b) Montrons que le quadrilatère $AKBI$ est un losange.
D'après la question $1)$, on a : $\overrightarrow{IK}=\overrightarrow{IA}+\overrightarrow{IB}$
Ce qui entraine : $\overrightarrow{IK}-\overrightarrow{IA}=\overrightarrow{IB}$
Or, on sait que : $-\overrightarrow{IA}=\overrightarrow{AI}$
Par suite,
$\begin{array}{rcl} \overrightarrow{IK}-\overrightarrow{IA}=\overrightarrow{IB}&\Leftrightarrow&\overrightarrow{IK}+\overrightarrow{AI}=\overrightarrow{IB}\\\\&\Leftrightarrow&\overrightarrow{AI}+\overrightarrow{IK}=\overrightarrow{IB}\\\\&\Leftrightarrow&\overrightarrow{AK}=\overrightarrow{IB}\end{array}$
Ainsi, $\boxed{\overrightarrow{AK}=\overrightarrow{IB}}$
D'où, le quadrilatère $AKBI$ est un parallélogramme.
Par ailleurs, $ABCD$ étant un rectangle de centre $I$ alors, les diagonales $[AC]\ $ et $\ [DB]$ ont même milieu $I$ et sont de même longueur.
Ce qui entraine alors : $IA=IB$
Ainsi, le quadrilatère $AKBI$ est un parallélogramme qui a deux côtés consécutifs de même longueur.
Par conséquent, c'est un losange.
2) a) Construisons le point $P$, symétrique de $I$ par rapport à $B$, et le point $R$, symétrique de $K$ par rapport à $B.$
b) Prouvons que les points $I\;,\ K\;,\ P\ $ et $\ R$ sont sur un même cercle. Indiquons le centre et le rayon de ce cercle.
En effet, on a : $P$, symétrique de $I$ par rapport à $B$ donc, le point $B$ est le milieu de $[IP].$
Ainsi, $\overrightarrow{IB}=\overrightarrow{BP}$
Par suite, $IB=PB$
On a aussi : $R$, symétrique de $K$ par rapport à $B$ donc, $B$ est milieu de $[KR].$
Ce qui signifie : $\overrightarrow{KB}=\overrightarrow{BR}$
Ainsi, $KB=RB$
Par ailleurs, d'après le résultat de la question $1)$, on sait que $AKBI$ est un losange.
Ce qui signifie que ses côtés ont même longueur.
Donc, $IB=KB$
D'où, on obtient :
$$IB=KB=RB=PB$$
On remarque alors que les points $I\;,\ K\;,\ P\ $ et $\ R$ sont à égale distance du point $B.$
Par conséquent, ces points appartiennent à un même cercle de centre $B$ et de rayon $BI.$
Construisons ce cercle sur la figure.
c) En déduisons la nature du quadrilatère $IKPR.$
En effet, d'après la question $2)\;a)$, le quadrilatère $IKPR$ a ses diagonales $[IP]\ $ et $\ [KR]$ de même milieu $B.$
Donc, c'est un parallélogramme.
De plus, d'après la question $2)\;b)$, on a : $IKPR$ inscriptible dans le cercle de centre $B$ et de rayon $BI.$
Ainsi, le quadrilatère $IKPR$ est un parallélogramme inscriptible dans un cercle.
Par conséquent, $IKPR$ est un rectangle.

Exercice 6
1) Construisons un triangle isocèle $ABC$ de sommet $A$ tel que : $AB=4.5\;cm\ $ et $\ BC=5.4\;cm$
Plaçons le point $H$, pied de la hauteur issue de $A$, et le point $M$, milieu de $[AB].$
2) Justifions que $H$ est le milieu de $[BC].$
En effet, la hauteur issue de $A$ coupe $[BC]$ au point $H.$
Comme le triangle $ABC$ est isocèle en $A$ alors, la hauteur issue de $A$ est en même temps médiatrice du segment $[BC].$
Or, la médiatrice de $[BC]$ passe par le milieu du segment $[BC].$
D'où, $H$ est le milieu de $[BC].$
3) Calculons la longueur du segment $[MH].$
On a : $H$, milieu de $[BC]\ $ et $\ M$, milieu de $[AB].$
Or, d'après une conséquence du théorème de la droite des milieux, le segment qui joint les milieux de deux côtés d'un triangle a pour longueur la moitié de la longueur du troisième côté.
Ce qui signifie que dans le triangle $ABC$, on a :
$$MH=\dfrac{AC}{2}$$
Comme $ABC$ est isocèle en $A$ alors, $AC=AB=4.5\;cm.$
Ainsi, $MH=\dfrac{4.5}{2}=2.25$
D'où, $\boxed{MH=2.25\;cm}$
4) Construisons le point $D$, symétrique du point $M$ par rapport au point $H.$
Le quadrilatère $BMCD$ est un parallélogramme.
Justifions la réponse.
En effet, comme $D$ est le symétrique du point $M$ par rapport au point $H$ alors, $H$ est milieu du segment $[MD].$
Or, d'après le résultat de la question $2)$, on a : $H$, milieu de $[BC].$
Donc, quadrilatère $BMCD$ a ses diagonales $[MD]\ $ et $\ [BC]$ de même milieu $H.$
Par conséquent, $BMCD$ est un parallélogramme.
5) Démontrons que : $\overrightarrow{AM}+\overrightarrow{BD}=\overrightarrow{MD}$
Suivant la relation de Chasles, décomposons le vecteur $\overrightarrow{BD}$ en utilisant le point $M.$ Ce qui donne alors :
$$\overrightarrow{BD}=\overrightarrow{BM}+\overrightarrow{MD}$$
Ainsi, en remplaçant $\overrightarrow{BD}$ par son expression, on obtient :
$$\overrightarrow{AM}+\overrightarrow{BD}=\overrightarrow{AM}+\overrightarrow{BM}+\overrightarrow{MD}$$
Comme $M$ est le milieu du segment $[AB]$ alors, on a :
$$\overrightarrow{AM}+\overrightarrow{BM}=\vec{0}$$
D'où, $\boxed{\overrightarrow{AM}+\overrightarrow{BD}=\overrightarrow{MD}}$

Exercice 7
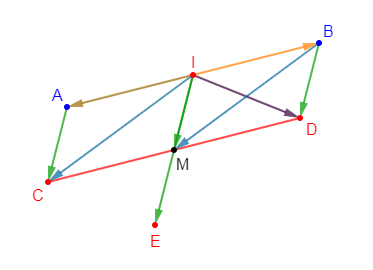
Soit $I$ le milieu d'un segment $[AB]$ et $M$ un point n'appartenant pas à $(AB).$
1)Construisons les points $C$ et $D$ tels que :
$$\overrightarrow{IC}=\overrightarrow{IA}+\overrightarrow{IM}\ \text{ et }\ \overrightarrow{ID}=\overrightarrow{IB}+\overrightarrow{IM}$$
2) Démontrons que $M$ est le milieu de $[CD]$
Soit : $\overrightarrow{IC}=\overrightarrow{IA}+\overrightarrow{IM}$ alors, on a :
$\begin{array}{rcl}\overrightarrow{IC}-\overrightarrow{IM}=\overrightarrow{IA}&\Leftrightarrow&\overrightarrow{IC}+\overrightarrow{MI}=\overrightarrow{IA}\\\\&\Leftrightarrow&\overrightarrow{MI}+\overrightarrow{IC}=\overrightarrow{IA}\\\\&\Leftrightarrow&\overrightarrow{MC}=\overrightarrow{IA}\end{array}$
Donc, $\boxed{\overrightarrow{MC}=\overrightarrow{IA}\quad(1)}$
On a : $\overrightarrow{ID}=\overrightarrow{IB}+\overrightarrow{IM}.$
Alors,
$\begin{array}{rcl}\overrightarrow{ID}-\overrightarrow{IM}=\overrightarrow{IB}&\Leftrightarrow&\overrightarrow{ID}+\overrightarrow{MI}=\overrightarrow{IB}\\\\&\Leftrightarrow&\overrightarrow{MI}+\overrightarrow{ID}=\overrightarrow{IB}\\\\&\Leftrightarrow&\overrightarrow{MD}=\overrightarrow{IB}\end{array}$
Donc, $\boxed{\overrightarrow{MD}=\overrightarrow{IB}\quad(2)}$
En additionnant les égalités $(1)\ $ et $\ (2)$, on obtient :
$$\overrightarrow{MC}+\overrightarrow{MD}=\overrightarrow{IA}+\overrightarrow{IB}$$
Comme $I$ est le milieu de $[AB]$ alors, on a :
$$\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$$
D'où, $\boxed{\overrightarrow{MC}+\overrightarrow{MD}=\vec{0}}$
Ce qui démontre que $M$ est le milieu du segment $[CD].$
3) Démontrons que $\overrightarrow{IC}=\overrightarrow{BM}$
En effet, on a : $\overrightarrow{IC}=\overrightarrow{IA}+\overrightarrow{IM}.$
Comme $I$ est milieu de $[AB]$ alors, on a :
$$\overrightarrow{IA}=\overrightarrow{BI}$$
Ainsi, en remplaçant $\overrightarrow{IA}$ par $\overrightarrow{BI}$, on obtient :
$$\overrightarrow{IC}=\overrightarrow{BI}+\overrightarrow{IM}$$
Or, d'après la relation de Chasles, on a :
$$\overrightarrow{BI}+\overrightarrow{IM}=\overrightarrow{BM}$$
Par conséquent, $\boxed{\overrightarrow{IC}=\overrightarrow{BM}}$
4) Soit $E$ le symétrique de $I$ par rapport à $M.$ Démontrons que $\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{IE}$
D'après le résultat de la question $2)\;,\ M$ est le milieu du segment $[CD].$
Donc, d'après une propriété du cours, on a :
$$\overrightarrow{IC}+\overrightarrow{ID}=2\overrightarrow{IM}$$
Par ailleurs, comme $E$ est le symétrique de $I$ par rapport à $M$ alors, $M$ est milieu de $[IE].$
D'où,
$$2\overrightarrow{IM}=\overrightarrow{IE}$$
Et par conséquent, $\boxed{\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{IE}}$

Exercice 8
$A\;,\ B\ $ et $\ C$ sont trois points non alignés.
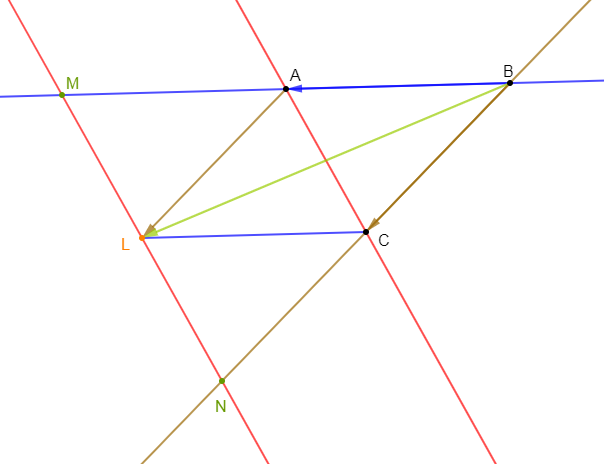
1) Construisons le point $L$ tel que $\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BL}$
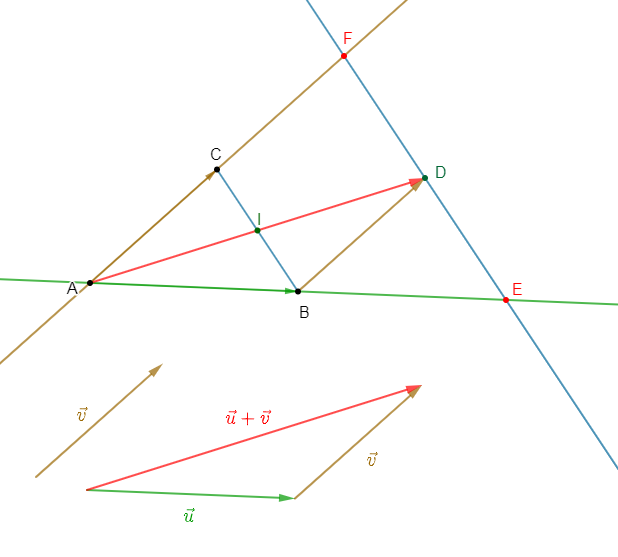
2) La parallèle à $(AC)$ passant par $L$ coupe $(BA)$ en $M\ $ et $\ (BC)$ en $N.$
Démontrons que $\overrightarrow{AC}=\overrightarrow{ML}=\overrightarrow{LN}$
D'après la question $1)$, on a : $\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BL}.$
Donc, le quadrilatère $BALC$ est un parallélogramme.
D'où, $(BA)$ parallèle à $(CL)\ $ et $\ (BC)$ parallèle à $(AL).$
Comme $M\in(BA)$ alors, $(AM)$ est aussi parallèle à $(CL).$
Par ailleurs, on a : $(ML)$ parallèle à $(AC).$
Ainsi, le quadrilatère $AMLC$ a ses côtés deux à deux parallèles.
Par conséquent, c'est un parallélogramme.
D'où, $\boxed{\overrightarrow{AC}=\overrightarrow{ML}}$
De la même manière, comme $N\in(BC)$ alors, $(CN)$ est parallèle à $(AL).$
Or, on a : $(NL)$ parallèle à $(AC).$
Donc, le quadrilatère $ALNC$ a ses côtés deux à deux parallèles.
Par conséquent, c'est un parallélogramme.
D'où, $\boxed{\overrightarrow{AC}=\overrightarrow{LN}}$
Ainsi, on a : $\overrightarrow{AC}=\overrightarrow{ML}\ $ et $\ \overrightarrow{AC}=\overrightarrow{LN}$
Ce qui montre que $\boxed{\overrightarrow{AC}=\overrightarrow{ML}=\overrightarrow{LN}}$

Exercice 9
Soit $ABC$ un triangle ; $\vec{u}\ $ et$\ \vec{v}$ deux vecteurs tels que $\vec{u}=\overrightarrow{AB}\ $ et $\ \vec{v}=\overrightarrow{AC}$
Soit $I$ le milieu de $[BC].$
1) Démontrons que $\vec{u}+\vec{v}=2\overrightarrow{AI}$
En effet, comme $\vec{u}=\overrightarrow{AB}\ $ et $\ \vec{v}=\overrightarrow{AC}$ alors, on a :
$\vec{u}+\vec{v}=\overrightarrow{AB}+\overrightarrow{AC}$
Par ailleurs, on a : $I$ le milieu de $[BC].$
Ce qui signifie :
$$\overrightarrow{IB}+\overrightarrow{IC}=\vec{0}$$
Donc, suivant la relation de Chasles, on décompose les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$ en utilisant le point $I.$
Ce qui donne alors :
$\overrightarrow{AB}=\overrightarrow{AI}+\overrightarrow{IB}$
$\overrightarrow{AC}=\overrightarrow{AI}+\overrightarrow{IC}$
Ainsi, on a :
$\begin{array}{rcl}\vec{u}+\vec{v}&=&\overrightarrow{AB}+\overrightarrow{AC}\\\\&=&\left(\overrightarrow{AI}+\overrightarrow{IB}\right)+\left(\overrightarrow{AI}+\overrightarrow{IC}\right)\\\\&=&\overrightarrow{AI}+\overrightarrow{IB}+\overrightarrow{AI}+\overrightarrow{IC}\\\\&=&2\overrightarrow{AI}+\underbrace{\overrightarrow{IB}+\overrightarrow{IC}}_{=\vec{0}}\\\\&=&2\overrightarrow{AI}+\vec{0}\\\\&=&2\overrightarrow{AI}\end{array}$
D'où, $\boxed{\vec{u}+\vec{v}=2\overrightarrow{AI}}$
2) Soit $D$ le point tel que $\vec{u}+\vec{v}=\overrightarrow{AD}$ ; la parallèle à $(BC)$ passant par $D$ coupe $(AB)$ en $E\ $ et $\ (AC)$ en $F.$
Démontrons que $\overrightarrow{AE}=2\overrightarrow{AB}\ $ et $\ \overrightarrow{AF}=2\overrightarrow{AC}$
Soit : $\vec{u}+\vec{v}=\overrightarrow{AD}.$
D'après le résultat de la question $1)$, on a : $\vec{u}+\vec{v}=2\overrightarrow{AI}.$
Donc, $\overrightarrow{AD}=2\overrightarrow{AI}$
Ce qui signifie que $I$ est milieu de $[AD].$
Par ailleurs, la parallèle à $(BC)$ passant par $D$ coupe $(AB)$ en $E.$ Donc, on a : $(DE)$ parallèle à $(BC).$
Ainsi, dans le triangle $ADE$, comme $(BC)$ passe par $I$ milieu de $[AD]$ alors, d'après la réciproque du théorème de la droite des milieux, $(BC)$ passe par le milieu de $[AE].$
Ainsi, $B$ est milieu de $[AE].$
D'où, $\boxed{\overrightarrow{AE}=2\overrightarrow{AB}}$
De la même manière, comme la parallèle à $(BC)$ passant par $D$ coupe $(AC)$ en $F$ alors, on a : $(DF)$ parallèle à $(BC).$
Donc, en considérant le triangle $ADF$, on a : $(BC)$ parallèle à $(DF)$, passe par $I$ milieu de $[AD].$
Ainsi, d'après la réciproque du théorème de la droite des milieux, $(BC)$ passe par le milieu de $[AF].$
D'où, $C$ est milieu de $[AF].$
Par conséquent, $\boxed{\overrightarrow{AF}=2\overrightarrow{AC}}$
3) Déterminons le réel $k$ tel que $\overrightarrow{EF}=k\overrightarrow{CB}$
D'après le résultat de la question $2)$, on a :
$\overrightarrow{AE}=2\overrightarrow{AB}\quad(1)$
$\overrightarrow{AF}=2\overrightarrow{AC}\quad(2)$
En multipliant l'égalité $(2)$ par $-1$, on obtient :
$\begin{array}{rcl} \overrightarrow{AF}=2\overrightarrow{AC}&\Leftrightarrow&-\overrightarrow{AF}=-2\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{FA}=2\overrightarrow{CA}\end{array}$
Donc, $\overrightarrow{FA}=2\overrightarrow{CA}\quad(3)$
Ainsi, en additionnant membre à membre les égalités $(1)\ $ et $\ (3)$, on trouve :
$\begin{array}{rcl} \overrightarrow{AE}+\overrightarrow{FA}=2\overrightarrow{AB}+2\overrightarrow{CA}&\Leftrightarrow&\overrightarrow{FA}+\overrightarrow{AE}=2\overrightarrow{CA}+2\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{FE}=2\left(\overrightarrow{CA}+\overrightarrow{AB}\right)\\\\&\Leftrightarrow&\overrightarrow{FE}=2\overrightarrow{CB}\end{array}$
D'où, $\boxed{\overrightarrow{FE}=2\overrightarrow{CB}}$
Par conséquent, $k=2$
4) Démontrons que $\overrightarrow{AE}+\overrightarrow{AF}=4\overrightarrow{AI}$
D'après le résultat de la question $2)$, on a :
$\overrightarrow{AE}=2\overrightarrow{AB}\quad(1)$
$\overrightarrow{AF}=2\overrightarrow{AC}\quad(2)$
Alors, en additionnant membre à membre les égalités $(1)\ $ et $\ (2)$, on obtient :
$\begin{array}{rcl} \overrightarrow{AE}+\overrightarrow{AF}&=&2\overrightarrow{AB}+2\overrightarrow{AC}\\\\&=&2\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\\\\&=&2\left(\vec{u}+\vec{v}\right)\\\\&=&2\times\left(2\overrightarrow{AI}\right)\\\\&=&4\overrightarrow{AI}\end{array}$
D'où, $\boxed{\overrightarrow{AE}+\overrightarrow{AF}=4\overrightarrow{AI}}$

Exercice 10
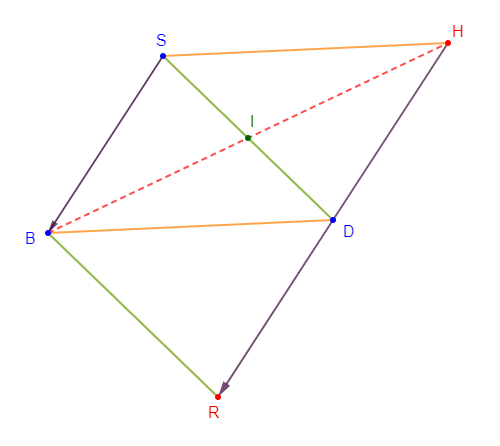
1) Traçons un triangle $BDS$ et marquons le milieu $I$ du segment $[SD]$
2) Construisons le point $H$ symétrique du point $B$ par rapport à $I.$
3) Démontrons que $\overrightarrow{HD}=\overrightarrow{SB}$
On a : $H$ symétrique du point $B$ par rapport à $I$ donc, le point $I$ est milieu de $[BH].$
Or, d'après la question $1)$, on a : $I$ milieu du segment $[SD].$
Donc, le quadrilatère $BDHS$ a ses diagonales $[SD]\ $ et $\ [BH]$ de même milieu $I.$
Par conséquent, $BDHS$ est un parallélogramme.
D'où, $\boxed{\overrightarrow{HD}=\overrightarrow{SB}}$
4) Construisons le point $R$, image du point $D$ par la translation de vecteur $\overrightarrow{SB}$
5) Démontrons que le point $D$ est le milieu du segment $[HR].$
On a : $t_{_{\overrightarrow{SB}}}(D)=R.$
Cela signifie que : $\overrightarrow{SB}=\overrightarrow{DR}$
Or, d'après le résultat de la question $3)$, on a : $\overrightarrow{HD}=\overrightarrow{SB}$
Donc, $\overrightarrow{HD}=\overrightarrow{DR}$
Ce qui montre que le point $D$ est le milieu du segment $[HR].$

Exercice 14
Simplifier les expressions suivantes en précisant les propriétés de l'addition vectorielle utilisées.
Soit : $\vec{E}_{1}=\overrightarrow{AB}-\overrightarrow{EG}+\overrightarrow{BC}+\overrightarrow{FG}-\overrightarrow{FE}+\vec{0}-\overrightarrow{AC}$
Alors, d'après la propriété de l'addition vectorielle sur l'opposé d'un vecteur, on a :
$-\overrightarrow{EG}=\overrightarrow{GE}$
$-\overrightarrow{FE}=\overrightarrow{EF}$
$-\overrightarrow{AC}=\overrightarrow{CA}$
Ce qui donne :
$\vec{E}_{1}=\overrightarrow{AB}+\overrightarrow{GE}+\overrightarrow{BC}+\overrightarrow{FG}+\overrightarrow{EF}+\vec{0}+\overrightarrow{CA}$
L'addition vectorielle étant commutative alors, $\vec{E}_{1}$ peut encore s'écrire :
$\vec{E}_{1}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{GE}+\overrightarrow{EF}+\overrightarrow{FG}+\vec{0}$
Comme $\vec{0}$ est l'élément neutre de l'addition vectorielle alors, on a :
$\vec{E}_{1}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{GE}+\overrightarrow{EF}+\overrightarrow{FG}$
Ensuite, en utilisant l'associativité et la relation de Chasles, on trouve :
$\begin{array}{rcl}\vec{E}_{1}&=&\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{GE}+\overrightarrow{EF}+\overrightarrow{FG}\\\\&=&\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{CA}+\left(\overrightarrow{GE}+\overrightarrow{EF}\right)+\overrightarrow{FG}\\\\&=&\overrightarrow{AC}+\overrightarrow{CA}+\overrightarrow{GF}+\overrightarrow{FG}\\\\&=&\overrightarrow{AA}+\overrightarrow{GG}\\\\&=&\vec{0}+\vec{0}\\\\&=&\vec{0}\end{array}$
D'où, $\boxed{\vec{E}_{1}=\vec{0}}$
Soit : $\vec{E}_{2}=5\sqrt{3}\overrightarrow{AB}-2\sqrt{2}\overrightarrow{DC}-2\sqrt{3}\overrightarrow{BA}-5\sqrt{2}\overrightarrow{DC}.$
Alors, d'après la propriété de l'addition vectorielle sur l'opposé d'un vecteur, on a :
$-2\sqrt{2}\overrightarrow{DC}=2\sqrt{2}\overrightarrow{CD}$
$-2\sqrt{3}\overrightarrow{BA}=2\sqrt{3}\overrightarrow{AB}$
$-5\sqrt{2}\overrightarrow{DC}=5\sqrt{2}\overrightarrow{CD}$
Ainsi, $\vec{E}_{2}$ s'écrit :
$\vec{E}_{2}=5\sqrt{3}\overrightarrow{AB}+2\sqrt{2}\overrightarrow{CD}+2\sqrt{3}\overrightarrow{AB}+5\sqrt{2}\overrightarrow{CD}.$
Comme l'addition vectorielle est commutative alors, on obtient :
$\begin{array}{rcl}\vec{E}_{2}&=&5\sqrt{3}\overrightarrow{AB}+2\sqrt{2}\overrightarrow{CD}+2\sqrt{3}\overrightarrow{AB}+5\sqrt{2}\overrightarrow{CD}\\\\&=&5\sqrt{3}\overrightarrow{AB}+2\sqrt{3}\overrightarrow{AB}+2\sqrt{2}\overrightarrow{CD}+5\sqrt{2}\overrightarrow{CD}\\\\&=&7\sqrt{3}\overrightarrow{AB}+7\sqrt{2}\overrightarrow{CD}\end{array}$
D'où, $\boxed{\vec{E}_{2}=7\sqrt{3}\overrightarrow{AB}+7\sqrt{2}\overrightarrow{CD}}$
Exercice 15
Répondons par vrai on faux en justifiant la réponse
1) Si $ABCD$ est un parallélogramme alors : $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{DB}.\quad\text{faux}$
En effet, d'après la relation de Chasles, on a :
$$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$$
Or, si $ABCD$ est un parallélogramme alors , les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{BC}$ sont différents car, ils ne sont ni de même direction, ni de même sens.
Par conséquent, la proposition est fausse.
2) Si $E\;,\ D\ $ et $\ F$ sont trois points distincts du plan, d'après la relation de Chasles, on a : $$\overrightarrow{DE}+\overrightarrow{DF}=\overrightarrow{EF}\quad\text{faux}$$
En effet, pour appliquer la relation de Chasles, il faut que l'origine de l'un des vecteurs soit l'extrémité de l'autre vecteur. Ce qui n'est pas le cas ici.
D'où, la proposition est fausse.
Au fait, la relation devait s'écrire :
$$\overrightarrow{DE}+\overrightarrow{EF}=\overrightarrow{DF}$$
3) Le vecteur $\overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{CB}$ est un vecteur nul.$\quad\text{vrai}$
On a :
$-\overrightarrow{AC}=\overrightarrow{CA}$
$-\overrightarrow{CB}=\overrightarrow{BC}$
Donc, on peut écrire :
$\begin{array}{rcl} \overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{CB}&=&\overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{BC}\\\\&=&\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\\\\&=&\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{CA}\\\\&=&\overrightarrow{AC}+\overrightarrow{CA}\\\\&=&\overrightarrow{AA}\\\\&=&\vec{0}\end{array}$
Ainsi, $\boxed{\overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{CB}=\vec{0}}$
D'où, la proposition est vraie.
4) Si $ABCD$ est un parallélogramme de centre $O$ alors : $\overrightarrow{AB}+\overrightarrow{AD}=2\overrightarrow{OC}\quad\text{vrai}$
Comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$$
Par ailleurs, $O$ est le centre du parallélogramme donc, $O$ est milieu de $[AC].$
D'où, $\overrightarrow{AC}=2\overrightarrow{OC}$
Ainsi, $\overrightarrow{AB}+\overrightarrow{AD}=2\overrightarrow{OC}$
Ce qui montre que la proposition est vraie.
5) Si $\overrightarrow{AE}=\overrightarrow{RS}$ alors, les segments $[AS]\ $ et $\ [RE]$ ont le même milieu.$\quad\text{vrai}$
En effet, si $\overrightarrow{AE}=\overrightarrow{RS}$ alors, $AESR$ est un parallélogramme.
D'où, ses diagonales $[AS]\ $ et $\ [RE]$ ont le même milieu.
Ainsi, la proposition est vraie.
Exercice 16
Démontrons chacune des égalités suivantes.
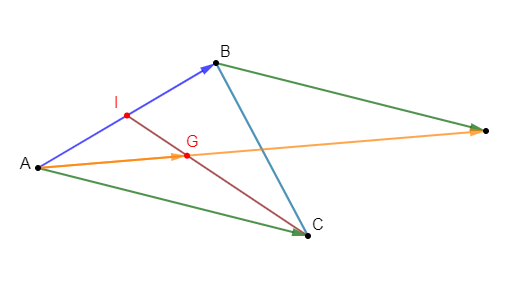
1) $\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}$
Suivant la relation de Chasles, décomposons les vecteurs $\overrightarrow{AC}\ $ et $\ \overrightarrow{BD}$ en utilisant respectivement les points $D\ $ et $\ C.$ Ce qui donne :
$\overrightarrow{AC}=\overrightarrow{AD}+\overrightarrow{DC}$
$\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}$
On remplace ensuite, $\overrightarrow{AC}\ $ et $\ \overrightarrow{BD}$ par leur expression puis on calcule la somme vectorielle $\overrightarrow{AC}+\overrightarrow{BD}$
On obtient alors :
$\begin{array}{rcl} \overrightarrow{AC}+\overrightarrow{BD}&=&\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{BC}+\overrightarrow{CD}\\\\&=&\overrightarrow{AD}+\overrightarrow{BC}+\overrightarrow{DC}+\overrightarrow{CD}\\\\&=&\overrightarrow{AD}+\overrightarrow{BC}+\overrightarrow{DD}\\\\&=&\overrightarrow{AD}+\overrightarrow{BC}+\vec{0}\\\\&=&\overrightarrow{AD}+\overrightarrow{BC}\end{array}$
D'où, $\boxed{\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}}$
2) $\overrightarrow{MA}+2\overrightarrow{MB}-3\overrightarrow{MC}=2\overrightarrow{AB}-3\overrightarrow{AC}$
Suivant la relation de Chasles, décomposons les vecteurs $\overrightarrow{MB}\ $ et $\ \overrightarrow{MC}$ en utilisant le point $A.$ Ce qui donne alors :
$\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AB}$
$\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AC}$
Ainsi, en remplaçant, $\overrightarrow{MB}\ $ et $\ \overrightarrow{MC}$ par leur expression, on obtient :
$\begin{array}{rcl} \overrightarrow{MA}+2\overrightarrow{MB}-3\overrightarrow{MC}&=&\overrightarrow{MA}+2\left(\overrightarrow{MA}+\overrightarrow{AB}\right)-3\left(\overrightarrow{MA}+\overrightarrow{AC}\right)\\\\&=&\overrightarrow{MA}+2\overrightarrow{MA}+2\overrightarrow{AB}-3\overrightarrow{MA}-3\overrightarrow{AC}\\\\&=&3\overrightarrow{MA}-3\overrightarrow{MA}+2\overrightarrow{AB}-3\overrightarrow{AC}\\\\&=&2\overrightarrow{AB}-3\overrightarrow{AC}\end{array}$
D'où, $\boxed{\overrightarrow{MA}+2\overrightarrow{MB}-3\overrightarrow{MC}=2\overrightarrow{AB}-3\overrightarrow{AC}}$
Exercice 17
On donne les égalités vectorielles suivantes : $\overrightarrow{AB}=2\overrightarrow{CD}\ $ et $\ \overrightarrow{CD}=4\overrightarrow{EF}.$
1) Exprimons $\overrightarrow{AB}$ en fonction de $\overrightarrow{EF}.$
On a : $\overrightarrow{AB}=2\overrightarrow{CD}.$
Or, $\overrightarrow{CD}=4\overrightarrow{EF}.$
Donc, en remplaçant $\overrightarrow{CD}$ par $4\overrightarrow{EF}$, on obtient :
$\begin{array}{rcl} \overrightarrow{AB}&=&2\overrightarrow{CD}\\\\&=&2\times\left(4\overrightarrow{EF}\right)\\\\&=&2\times 4\overrightarrow{EF}\\\\&=&8\overrightarrow{EF}\end{array}$
Ainsi, $\boxed{\overrightarrow{AB}=8\overrightarrow{EF}}$
2) Exprimons $\overrightarrow{EF}$ en fonction de $\overrightarrow{AB}$
D'après le résultat de la question $1)$, on a : $\overrightarrow{AB}=8\overrightarrow{EF}.$
Par conséquent, $\boxed{\overrightarrow{EF}=\dfrac{\overrightarrow{AB}}{8}}$
3) Concluons
D'après les questions précédentes, on a : $\overrightarrow{AB}=8\overrightarrow{EF}\ $ et $\ \overrightarrow{EF}=\dfrac{\overrightarrow{AB}}{8}.$
Cela signifie que les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{EF}$ sont de même direction, de même sens et que la longueur du vecteur $\overrightarrow{AB}$ est égale à $8$ fois la longueur du vecteur $\overrightarrow{EF}.$
On peut alors conclure que ces deux vecteurs sont colinéaires, ou encore les droites $(AB)\ $ et $\ (EF)$ sont parallèles.
Exercice 18
Soit $ABC$ un triangle tel que: $AB=2\;cm\;;\ AC=3\;cm\ $ et $\ BC=4\;cm.$
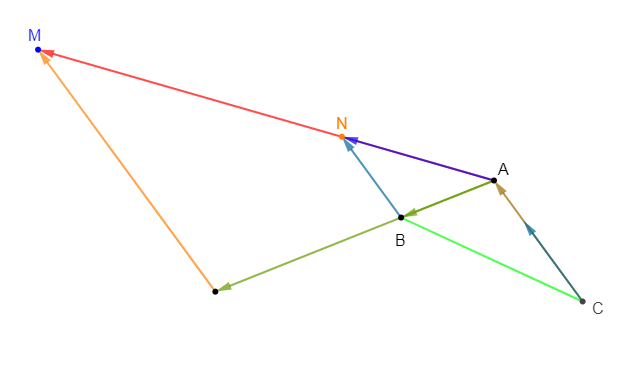
1) Construisons le point $M$ tel que : $\overrightarrow{AM}=3\overrightarrow{AB}+2\overrightarrow{CA}$
2) Construisons le point $M$ tel que : $\overrightarrow{AN}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{CA}$
3) Montrons que : $\overrightarrow{AM}=3\overrightarrow{AN}$
En multipliant le vecteur $\overrightarrow{AN}$ par $3$, on obtient :
$\begin{array}{rcl} 3\times\overrightarrow{AN}&=&3\times\left(\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{CA}\right)\\\\&=&3\times\overrightarrow{AB}+3\times\left(\dfrac{2}{3}\overrightarrow{CA}\right)\\\\&=&3\overrightarrow{AB}+\dfrac{3\times 2}{3}\overrightarrow{CA}\\\\&=&3\overrightarrow{AB}+2\overrightarrow{CA}\end{array}$
Donc, $\boxed{3\overrightarrow{AN}=3\overrightarrow{AB}+2\overrightarrow{CA}}$
Or, d'après la question $1)$, on a : $\overrightarrow{AM}=3\overrightarrow{AB}+2\overrightarrow{CA}$
Par conséquent, $\overrightarrow{AM}=3\overrightarrow{AN}$
En déduisons que les points $A\;,\ M\ $ et $\ N$ sont alignés.
Comme $\overrightarrow{AM}=3\overrightarrow{AN}$ alors, on dit que les vecteurs $\overrightarrow{AM}\ $ et $\ \overrightarrow{AN}$ sont colinéaires.
D'où, les points $A\;,\ M\ $ et $\ N$ sont alignés.

Exercice 19
$ABC$ est un triangle et $G$ le point du plan tel que : $\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\vec{0}.$
1) Montrons que le point $G$ est unique.
Pour cela, choisissons un autre point $G'$ vérifiant la relation.
Donc, en remplaçant $G$ par $G'$, on obtient :
$$\overrightarrow{AG'}+\overrightarrow{BG'}+\overrightarrow{CG'}=\vec{0}$$
Suivant la relation de Chasles, décomposons les vecteurs $\overrightarrow{AG'}\;,\ \overrightarrow{BG'}$ et $\ \overrightarrow{CG'}$ en utilisant le point $G.$
On a alors :
$\overrightarrow{AG'}=\overrightarrow{AG}+\overrightarrow{GG'}$
$\overrightarrow{BG'}=\overrightarrow{BG}+\overrightarrow{GG'}$
$\overrightarrow{CG'}=\overrightarrow{CG}+\overrightarrow{GG'}$
Ainsi, on trouve :
$\begin{array}{rcl} \overrightarrow{AG'}+\overrightarrow{BG'}+\overrightarrow{CG'}=\vec{0}&\Leftrightarrow&\left(\overrightarrow{AG}+\overrightarrow{GG'}\right)+\left(\overrightarrow{BG}+\overrightarrow{GG'}\right)+\left(\overrightarrow{CG}+\overrightarrow{GG'}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AG}+\overrightarrow{GG'}+\overrightarrow{BG}+\overrightarrow{GG'}+\overrightarrow{CG}+\overrightarrow{GG'}=\vec{0}\\\\&\Leftrightarrow&\underbrace{\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}}_{=\vec{0}}+3\overrightarrow{GG'}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{GG'}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{GG'}=\vec{0}\end{array}$
Donc, $\overrightarrow{AG'}+\overrightarrow{BG'}+\overrightarrow{CG'}=\vec{0}$ si, et seulement si, $\overrightarrow{GG'}=\vec{0}.$
Or, $\overrightarrow{GG'}=\vec{0}$ signifie que $G=G'$
Par conséquent, $G$ est unique.
2) Construisons le point $G.$
Soit $G$ vérifiant : $\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\vec{0}$
Alors, suivant la relation de Chasles, décomposons les vecteurs $\overrightarrow{BG}\ $ et $\ \overrightarrow{CG}$ en utilisant le point $A.$ Ce qui donne :
$\overrightarrow{BG}=\overrightarrow{BA}+\overrightarrow{AG}$
$\overrightarrow{CG}=\overrightarrow{CA}+\overrightarrow{AG}$
Ainsi, on a :
$\begin{array}{rcl} \overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\vec{0}&\Leftrightarrow&\overrightarrow{AG}+\left(\overrightarrow{BA}+\overrightarrow{AG}\right)+\left(\overrightarrow{CA}+\overrightarrow{AG}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AG}+\overrightarrow{BA}+\overrightarrow{AG}+\overrightarrow{CA}+\overrightarrow{AG}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{AG}+\overrightarrow{BA}+\overrightarrow{CA}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{AG}=-\overrightarrow{BA}-\overrightarrow{CA}\\\\&\Leftrightarrow&3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{AG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}\end{array}$
Donc, $G$ est tel que : $\boxed{\overrightarrow{AG}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)}$
Remarque : $G$ est le centre de gravité du triangle $ABC.$

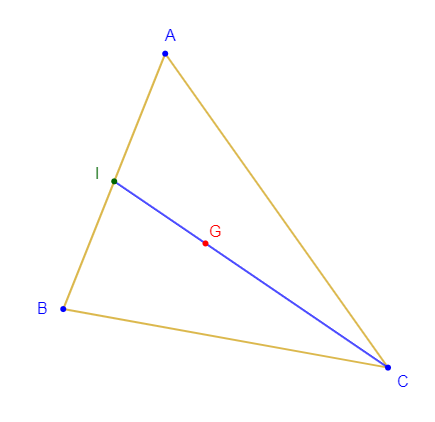
3) Soit $I$ milieu de $[AB]$ ; montrer que : $\overrightarrow{IG}=\dfrac{1}{2}\overrightarrow{GC}.$
Comme $I$ est le milieu du segment $[AB]$ alors, on a :
$$\overrightarrow{AI}+\overrightarrow{BI}=\vec{0}$$
Par ailleurs, $G$ vérifie : $\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\vec{0}$
Donc, suivant la relation de Chasles, décomposons les vecteurs $\overrightarrow{AG}\ $ et $\ \overrightarrow{BG}$ en utilisant le point $I.$
On a alors :
$\overrightarrow{AG}=\overrightarrow{AI}+\overrightarrow{IG}$
$\overrightarrow{BG}=\overrightarrow{BI}+\overrightarrow{IG}$
Ainsi, on a :
$\begin{array}{rcl} \overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\vec{0}&\Leftrightarrow&\left(\overrightarrow{AI}+\overrightarrow{IG}\right)+\left(\overrightarrow{BI}+\overrightarrow{IG}\right)+\overrightarrow{CG}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AI}+\overrightarrow{IG}+\overrightarrow{BI}+\overrightarrow{IG}+\overrightarrow{CG}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{IG}+\underbrace{\overrightarrow{AI}+\overrightarrow{BI}}_{=\vec{0}}+\overrightarrow{CG}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{IG}+\overrightarrow{CG}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{IG}=-\overrightarrow{CG}\\\\&\Leftrightarrow&2\overrightarrow{IG}=\overrightarrow{GC}\\\\&\Leftrightarrow&\overrightarrow{IG}=\dfrac{\overrightarrow{GC}}{2}\end{array}$
D'où, $\boxed{\overrightarrow{IG}=\dfrac{1}{2}\overrightarrow{GC}}$
Exercice 20
1) On considère un triangle $ABC$, tel que : $AB=5\;cm\;;\ BC=6\;cm\ $ et $\ AC=7\;cm.$ Soit $I$ milieu de $[AB].$
Construisons le point $G$ centre gravité du triangle $ABC.$
En effet, on sait que le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet.
Or, dans le triangle $ABC\;,\ [CI]$ est la médiane issue de $C.$
Donc, le centre de gravité $G$ de ce triangle est tel que :
$$\overrightarrow{GC}=\dfrac{2}{3}\overrightarrow{CI}$$

2) Sachant que : $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}.$ Démontrons que pour tout point $M$ du plan, on a : $$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$$
Soit : $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}.$
Décomposons les vecteurs $\overrightarrow{GA}\;,\ \overrightarrow{GB}\ $ et $\ \overrightarrow{GC}$ en utilisant la relation de Chasles.
Soit $M$ un point du plan alors, on a :
$\overrightarrow{GA}=\overrightarrow{GM}+\overrightarrow{MA}$
$\overrightarrow{GB}=\overrightarrow{GM}+\overrightarrow{MB}$
$\overrightarrow{GC}=\overrightarrow{GM}+\overrightarrow{MC}$
Ainsi, en remplaçant $\overrightarrow{GA}\;,\ \overrightarrow{GB}\ $ et $\ \overrightarrow{GC}$ par leur expression, on trouve :
$\begin{array}{rcl} \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}&\Leftrightarrow&\left(\overrightarrow{GM}+\overrightarrow{MA}\right)+\left(\overrightarrow{GM}+\overrightarrow{MB}\right)+\left(\overrightarrow{GM}+\overrightarrow{MC}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{GM}+\overrightarrow{MA}+\overrightarrow{GM}+\overrightarrow{MB}+\overrightarrow{GM}+\overrightarrow{MC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+3\overrightarrow{GM}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=-3\overrightarrow{GM}\\\\&\Leftrightarrow&\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\end{array}$
D'où, $\boxed{\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}}$
Exercice 21
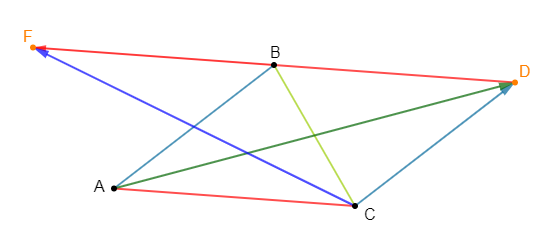
$ABC$ est un triangle quelconque, les points $D\ $ et $\ F$ sont tels que :
$$\overrightarrow{AD}=\overrightarrow{BC}-2\overrightarrow{BA}\ \text{ et }\ \overrightarrow{CF}=\overrightarrow{AB}-2\overrightarrow{AC}$$
1) Démontrons que :
a) $\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{AB}$
Soit : $\overrightarrow{AD}=\overrightarrow{BC}-2\overrightarrow{BA}.$
Alors, d'après la propriété de l'addition vectorielle sur l'opposé d'un vecteur, on a : $-2\overrightarrow{BA}=2\overrightarrow{AB}$
Ce qui donne :
$\begin{array}{rcl}\overrightarrow{AD}&=&\overrightarrow{BC}-2\overrightarrow{BA}\\\\&=&\overrightarrow{BC}+2\overrightarrow{AB}\\\\&=&\overrightarrow{BC}+\overrightarrow{AB}+\overrightarrow{AB}\\\\&=&\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AB}\\\\&=&\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}\\\\&=&\overrightarrow{AC}+\overrightarrow{AB}\end{array}$
D'où, $\boxed{\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{AB}}$
b) $\overrightarrow{CF}=\overrightarrow{CB}+\overrightarrow{CA}$
Soit : $\overrightarrow{CF}=\overrightarrow{AB}-2\overrightarrow{AC}.$
Alors, d'après la propriété de l'addition vectorielle sur l'opposé d'un vecteur, on a : $-2\overrightarrow{AC}=2\overrightarrow{CA}$
Ainsi, on obtient :
$\begin{array}{rcl}\overrightarrow{CF}&=&\overrightarrow{AB}-2\overrightarrow{AC}\\\\&=&\overrightarrow{AB}+2\overrightarrow{CA}\\\\&=&\overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{CA}\\\\&=&\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{CA}\\\\&=&\left(\overrightarrow{CA}+\overrightarrow{AB}\right)+\overrightarrow{CA}\\\\&=&\overrightarrow{CB}+\overrightarrow{CA}\end{array}$
D'où, $\boxed{\overrightarrow{CF}=\overrightarrow{CB}+\overrightarrow{CA}}$
2) Construisons les points $D\ $ et $\ F.$
D'après les résultats de la question $1)$, on a : les points $D\ $ et $\ F$ sont tels que :
$$\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{AB}\ \text{ et }\ \overrightarrow{CF}=\overrightarrow{CB}+\overrightarrow{CA}$$

3) En déduisons que le point $B$ est le milieu du segment $[DF].$
On a :
$\begin{array}{rcl} \overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{AB}&\Rightarrow&\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow{AC}\\\\&\Rightarrow&\overrightarrow{AD}+\overrightarrow{BA}=\overrightarrow{AC}\\\\&\Rightarrow&\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{AC}\\\\&\Rightarrow&\overrightarrow{BD}=\overrightarrow{AC}\end{array}$
Donc, $\boxed{\overrightarrow{BD}=\overrightarrow{AC}\quad(1)}$
On a aussi :
$\begin{array}{rcl} \overrightarrow{CF}=\overrightarrow{CB}+\overrightarrow{CA}&\Rightarrow&\overrightarrow{CF}-\overrightarrow{CB}=\overrightarrow{CA}\\\\&\Rightarrow&\overrightarrow{CF}+\overrightarrow{BC}=\overrightarrow{CA}\\\\&\Rightarrow&\overrightarrow{BC}+\overrightarrow{CF}=\overrightarrow{CA}\\\\&\Rightarrow&\overrightarrow{BF}=\overrightarrow{CA}\end{array}$
Donc, $\boxed{\overrightarrow{BF}=\overrightarrow{CA}\quad(2)}$
En additionnant les égalités $(1)\ $ et $\ (2)$, on obtient :
$\begin{array}{rcl} \overrightarrow{BD}+\overrightarrow{BF}&=&\overrightarrow{AC}+\overrightarrow{CA}\\\\&=&\overrightarrow{AA}\\\\&=&\vec{0}\end{array}$
Ainsi, $\boxed{\overrightarrow{BD}+\overrightarrow{BF}=\vec{0}}$
D'où, $B$ est le milieu du segment $[DF].$
Exercice 22
1) On considère un segment $[AB]$ de milieu $I$, démontrons que pour tout point $M$,
$$\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$$
En effet, $I$ étant milieu du segment $[AB]$ alors, on a :
$$\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$$
Soit $M$ un point du plan.
D'après la relation de Chasles, on peut écrire :
$\overrightarrow{IA}=\overrightarrow{IM}+\overrightarrow{MA}$
$\overrightarrow{IB}=\overrightarrow{IM}+\overrightarrow{MB}$
Ainsi, en remplaçant $\overrightarrow{IA}\ $ et $\ \overrightarrow{IB}$ par leur expression, on obtient :
$\begin{array}{rcl} \overrightarrow{IA}+\overrightarrow{IB}=\vec{0}&\Leftrightarrow&\left(\overrightarrow{IM}+\overrightarrow{MA}\right)+\left(\overrightarrow{IM}+\overrightarrow{MB}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{IM}+\overrightarrow{MA}+\overrightarrow{IM}+\overrightarrow{MB}\vec{0}\\\\&\Leftrightarrow&\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{IM}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{MA}+\overrightarrow{MB}=-2\overrightarrow{IM}\\\\&\Leftrightarrow&\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\end{array}$
D'où, $\boxed{\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}}$
2) $ABC$ est un triangle, on suppose qu'il existe un point $H$ tel que : $\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}$, en utilisant $I$ milieu de $[AB]$, démontrons que $H$ est un point de $[IC].$
Comme $I$ est le milieu du segment $[AB]$ alors, on a :
$$\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$$
Soit alors $H$ vérifiant : $\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}$
Donc, décomposons les vecteurs $\overrightarrow{HA}\;,\ \overrightarrow{HB}\ $ et $\ \overrightarrow{HC}$ en utilisant le point $I.$
On a alors :
$\overrightarrow{HA}=\overrightarrow{HI}+\overrightarrow{IA}$
$\overrightarrow{HB}=\overrightarrow{HI}+\overrightarrow{IB}$
$\overrightarrow{HC}=\overrightarrow{HI}+\overrightarrow{IC}$
Remplaçons ensuite, $\overrightarrow{HA}\;,\ \overrightarrow{HB}\ $ et $\ \overrightarrow{HC}$ par leur expression.
On obtient :
$\begin{array}{rcl} \overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}&\Leftrightarrow&\left(\overrightarrow{HI}+\overrightarrow{IA}\right)+\left(\overrightarrow{HI}+\overrightarrow{IB}\right)+\left(\overrightarrow{HI}+\overrightarrow{IC}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{HI}+\overrightarrow{IA}+\overrightarrow{HI}+\overrightarrow{IB}+\overrightarrow{HI}+\overrightarrow{IC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{HI}+\underbrace{\overrightarrow{IA}+\overrightarrow{IB}}_{=\vec{0}}+\overrightarrow{IC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{HI}+\overrightarrow{IC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{HI}=-\overrightarrow{IC}\\\\&\Leftrightarrow&3\overrightarrow{HI}=\overrightarrow{CI}\\\\&\Leftrightarrow&\overrightarrow{HI}=\dfrac{\overrightarrow{CI}}{3}\end{array}$
D'où, $\boxed{\overrightarrow{HI}=\dfrac{1}{3}\overrightarrow{CI}}$
Ce qui montre que $H$ est un point du segment $[IC].$
Exercice 23
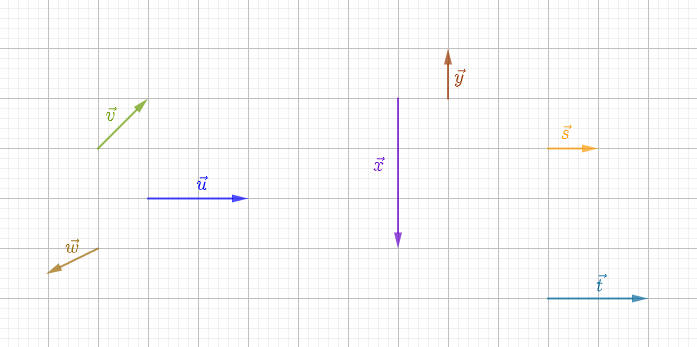
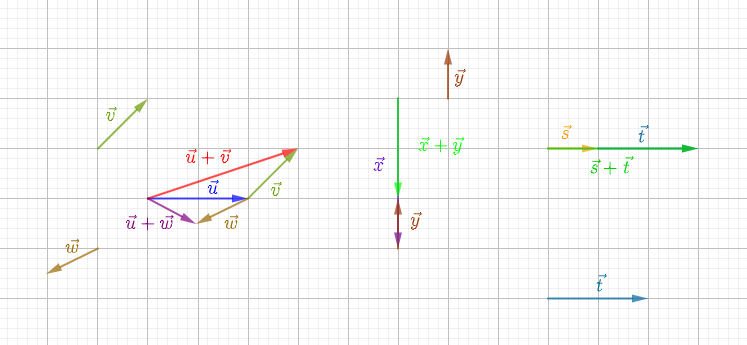
Reproduisons la figure ci-dessous en utilisant le quadrillage du cahier.

Construisons les vecteurs
$\overrightarrow{u}+\overrightarrow{v}$ ;
$\overrightarrow{x}+\overrightarrow{y}$ ;
$\overrightarrow{u}+\overrightarrow{w}$ ;
$\overrightarrow{s}+\overrightarrow{t}$

Exercice 24
a) Construisons un triangle $ABC$ tel que $AB=4\;cm\;,\ AC=3.5\;cm\ $ et $\ BC=3\;cm.$
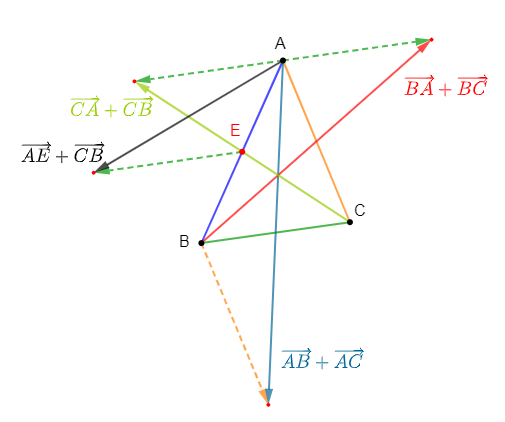
b) Construisons les vecteurs :
$$\overrightarrow{AB}+\overrightarrow{AC}\;;\ \overrightarrow{BA}+\overrightarrow{BC}\ \text{ et }\ \overrightarrow{CA}+\overrightarrow{CB}$$
c) Marquons le point $E$ milieu de $[AB]$ puis, construisons le vecteur $\overrightarrow{AE}+\overrightarrow{CB}$

Exercice 25
Soit $ABC$ un triangle.
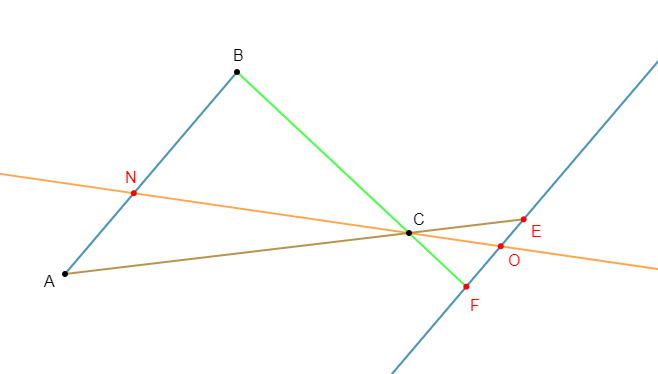
1) a) Construisons les points $E\ $ et $\ F$ tels que :
$$\overrightarrow{CE}=\dfrac{-1}{3}\overrightarrow{CA}\ \text{ et }\ \overrightarrow{CF}=\dfrac{-1}{3}\overrightarrow{CB}$$
b) Démontrons que les droites $(EF)\ $ et $\ (AB)$ sont parallèles.
Pour cela, il suffit de montrer que les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{AB}$ sont colinéaires.
Soit : $\overrightarrow{CE}=\dfrac{-1}{3}\overrightarrow{CA}.$
Alors, d'après la relation de Chasles, on peut décomposer le vecteur $\overrightarrow{CE}$ en utilisant le point $F.$
Ce qui donne : $\overrightarrow{CE}=\overrightarrow{CF}+\overrightarrow{FE}$
Ainsi, en remplaçant successivement $\overrightarrow{CE}\ $ et $\ \overrightarrow{CF}$ par leur expression, on obtient :
$\begin{array}{rcl} \overrightarrow{CE}=-\dfrac{1}{3}\overrightarrow{CA}&\Leftrightarrow&\overrightarrow{CF}+\overrightarrow{FE}=-\dfrac{1}{3}\overrightarrow{CA}\\\\&\Leftrightarrow&-\dfrac{1}{3}\overrightarrow{CB}+\overrightarrow{FE}=-\dfrac{1}{3}\overrightarrow{CA}\\\\&\Leftrightarrow&\overrightarrow{FE}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}\\\\&\Leftrightarrow&\overrightarrow{FE}=\dfrac{1}{3}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)\\\\&\Leftrightarrow&\overrightarrow{FE}=\dfrac{1}{3}\overrightarrow{AB}\\\\&\Leftrightarrow&\overrightarrow{EF}=-\dfrac{1}{3}\overrightarrow{AB}\end{array}$
Donc, $\boxed{\overrightarrow{EF}=-\dfrac{1}{3}\overrightarrow{AB}}$
Ce qui signifie que les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{AB}$ sont colinéaires.
Et par conséquent, les droites $(EF)\ $ et $\ (AB)$ sont parallèles.
2) a) Construisons les points $O\ $ et $\ N$ tels que :
$$\overrightarrow{EO}=\dfrac{2}{5}\overrightarrow{EF}\ \text{ et }\ \overrightarrow{AN}=\dfrac{2}{5}\overrightarrow{AB}$$
b) Démontrons que les points $C\;,\ O\ $ et $\ N$ sont alignés.
On a : $\overrightarrow{EO}=\dfrac{2}{5}\overrightarrow{EF}$
Or, d'après le résultat de la question $1)\;b)$, on a : $\overrightarrow{EF}=-\dfrac{1}{3}\overrightarrow{AB}$
Donc, en remplaçant $\overrightarrow{EF}$ par $-\dfrac{1}{3}\overrightarrow{AB}$, on trouve :
$\begin{array}{rcl} \overrightarrow{EO}&=&\dfrac{2}{5}\overrightarrow{EF}\\\\&=&\dfrac{2}{5}\left(-\dfrac{1}{3}\overrightarrow{AB}\right)\\\\&=&-\dfrac{1}{3}\left(\dfrac{2}{5}\overrightarrow{AB}\right)\end{array}$
Comme $\overrightarrow{AN}=\dfrac{2}{5}\overrightarrow{AB}$ alors, en remplaçant $\dfrac{2}{5}\overrightarrow{AB}$ par $\overrightarrow{AN}$, on obtient :
$$\overrightarrow{EO}=-\dfrac{1}{3}\overrightarrow{AN}$$
En utilisant le point $C$, on peut écrire :
$\overrightarrow{EO}=\overrightarrow{EC}+\overrightarrow{CO}$
$\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}$
Remplaçons ensuite, $\overrightarrow{EO}\ $ et $\ \overrightarrow{AN}$ par leur expression.
On obtient alors :
$\begin{array}{rcl} \overrightarrow{EO}=-\dfrac{1}{3}\overrightarrow{AN}&\Leftrightarrow&\overrightarrow{EC}+\overrightarrow{CO}=-\dfrac{1}{3}\left(\overrightarrow{AC}+\overrightarrow{CN}\right)\\\\&\Leftrightarrow&\overrightarrow{EC}+\overrightarrow{CO}=-\dfrac{1}{3}\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{CN}\\\\&\Leftrightarrow&\overrightarrow{CO}=-\overrightarrow{EC}+\dfrac{1}{3}\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CN}\\\\&\Leftrightarrow&\overrightarrow{CO}=\overrightarrow{CE}+\dfrac{1}{3}\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CN}\end{array}$
Ainsi, on a : $\boxed{\overrightarrow{CO}=\overrightarrow{CE}+\dfrac{1}{3}\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CN}}$
Comme $\overrightarrow{CE}=-\dfrac{1}{3}\overrightarrow{CA}$ alors, en remplaçant $\overrightarrow{CE}$ par $-\dfrac{1}{3}\overrightarrow{CA}$, on trouve :
$\begin{array}{rcl} \overrightarrow{CO}&=&\overrightarrow{CE}+\dfrac{1}{3}\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CN}\\\\&=&-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CN}\\\\&=&\vec{0}-\dfrac{1}{3}\overrightarrow{CN}\\\\&=&-\dfrac{1}{3}\overrightarrow{CN}\end{array}$
D'où, $\boxed{\overrightarrow{CO}=-\dfrac{1}{3}\overrightarrow{CN}}$
Ce qui signifie que les vecteurs $\overrightarrow{CO}\ $ et $\ \overrightarrow{CN}$ sont colinéaires.
Par conséquent, les points $C\;,\ O\ $ et $\ N$ sont alignés.

Exercice 26
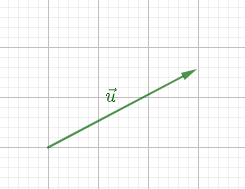
Reproduisons la figure ci-dessous en utilisant le quadrillage du cahier.

Construisons les vecteurs :
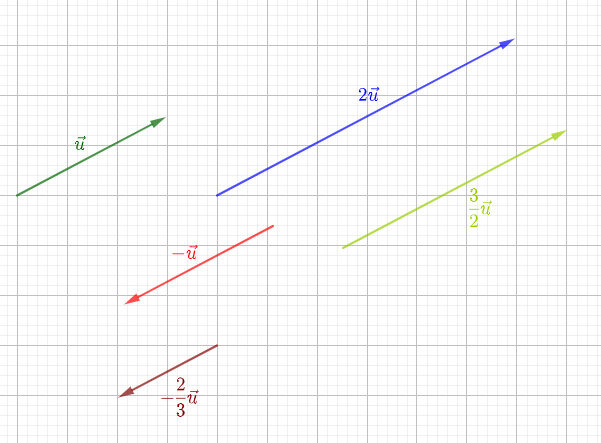
$2\overrightarrow{u}\;;\ \overrightarrow{-u}$ ;
$\dfrac{3}{2}\overrightarrow{u}\;;\ -\dfrac{2}{3}\overrightarrow{u}.$
En effet :
$-\ $ les vecteurs $2\vec{u}\ $ et $\ \vec{u}$ ont la même direction, le même sens et la longueur du vecteur $2\vec{u}$ est égale à $2$ fois la longueur du vecteur $\vec{u}.$
$-\ $ les vecteurs $-\vec{u}\ $ et $\ \vec{u}$ ont la même direction, la même longueur mais de sens opposés.
$-\ $ les vecteurs $\dfrac{3}{2}\vec{u}\ $ et $\ \vec{u}$ ont la même direction, le même sens et la longueur du vecteur $\dfrac{3}{2}\vec{u}$ est égale à $\dfrac{3}{2}$ fois la longueur du vecteur $\vec{u}.$
$-\ $ les vecteurs $-\dfrac{2}{3}\vec{u}\ $ et $\ \vec{u}$ ont la même direction, de sens opposés et la longueur du vecteur $-\dfrac{2}{3}\vec{u}$ est égale à $\dfrac{2}{3}$ fois la longueur du vecteur $\vec{u}.$

Exercice de Synthèse
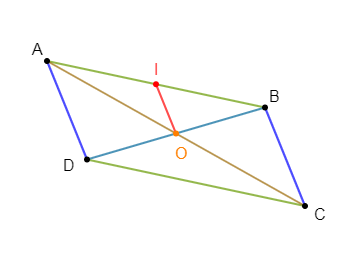
a) Traçons un parallélogramme $ABCD$ de centre $O.$
On note $I$ le milieu de $[AB].$

b) Simplifions les sommes vectorielles suivantes en seul vecteur
$\overrightarrow{OA}+\overrightarrow{OC}=\vec{0}$
En effet, comme $O$ est le centre du parallélogramme $ABCD$ alors, cela signifie que $O$ est le milieu de la diagonale $[AC].$
D'où, $\boxed{\overrightarrow{OA}+\overrightarrow{OC}=\vec{0}}$
$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$
Comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{AD}=\overrightarrow{BC}$$
Ainsi, en remplaçant $\overrightarrow{AD}$ par $\overrightarrow{BC}$
, on obtient :
$$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BC}$$
D'après la relation de Chasles, on trouve :
$$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$$
D'où, $\boxed{\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}}$
$\overrightarrow{CD}+\overrightarrow{CB}=\overrightarrow{CA}$
En effet, comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{CB}=\overrightarrow{DA}$$
Donc, en remplaçant $\overrightarrow{CB}$ par $\overrightarrow{DA}$
, on obtient :
$$\overrightarrow{CD}+\overrightarrow{CB}=\overrightarrow{CD}+\overrightarrow{DA}$$
Ensuite, en utilisant la relation de Chasles, on trouve :
$$\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{CA}$$
Par conséquent, $\boxed{\overrightarrow{CD}+\overrightarrow{CB}=\overrightarrow{CA}}$
$\overrightarrow{OI}+\overrightarrow{OI}+\overrightarrow{AD}=\vec{0}$
En effet, comme $ABCD$ est un parallélogramme de centre $O$ alors, $O$ est le milieu de $[DB].$
De plus, $I$ est milieu de $[AB].$
Donc, dans le triangle $ABD$, en appliquant le théorème de la droite des milieux, on obtient :
$$\overrightarrow{OI}=\dfrac{\overrightarrow{DA}}{2}$$
Ainsi, en remplaçant $\overrightarrow{OI}$ par $\dfrac{\overrightarrow{DA}}{2}$, on trouve :
$\begin{array}{rcl} \overrightarrow{OI}+\overrightarrow{OI}+\overrightarrow{AD}&=&\dfrac{\overrightarrow{DA}}{2}+\dfrac{\overrightarrow{DA}}{2}+\overrightarrow{AD}\\\\&=&\dfrac{\overrightarrow{DA}+\overrightarrow{DA}}{2}+\overrightarrow{AD}\\\\&=&\dfrac{\overrightarrow{2DA}}{2}+\overrightarrow{AD}\\\\&=&\overrightarrow{DA}+\overrightarrow{AD}\\\\&=&\vec{0}\end{array}$
D'où, $\boxed{\overrightarrow{OI}+\overrightarrow{OI}+\overrightarrow{AD}=\vec{0}}$
I. $ABCD$ est un parallélogramme alors :
a) $\overrightarrow{AB}=\overrightarrow{DC}$
c) $\overrightarrow{CB}=\overrightarrow{DA}$
II. Pour trois points quelconques du plan $M\;,\ N\ $ et $\ P\ :$
$\overrightarrow{MN}+\overrightarrow{NP}$ est égal à :
c) $\overrightarrow{MP}$
Auteur:
Diny Faye

Commentaires
maty (non vérifié)
dim, 05/19/2019 - 22:30
Permalien
exellent
Pape Elimane Sene (non vérifié)
dim, 06/13/2021 - 22:33
Permalien
Excellente
attouchi (non vérifié)
ven, 05/01/2020 - 14:39
Permalien
très interessant
Anonyme (non vérifié)
mar, 07/14/2020 - 22:15
Permalien
C'est très bien je me
Mady (non vérifié)
sam, 07/18/2020 - 14:29
Permalien
Solution de l'exercice 19 n
Anonyme (non vérifié)
mer, 08/05/2020 - 02:49
Permalien
C très intéressant
ibrahima BA (non vérifié)
mer, 08/26/2020 - 02:31
Permalien
excellent
Anonyme (non vérifié)
sam, 10/17/2020 - 11:51
Permalien
Pdf
Anonyme (non vérifié)
jeu, 04/01/2021 - 12:50
Permalien
Excellent travail! Ces
Anonyme (non vérifié)
dim, 04/11/2021 - 22:00
Permalien
Merci
Ndiogou (non vérifié)
mar, 07/06/2021 - 09:59
Permalien
Correction exercice 14,15,16,17,18,19,20
Anonyme (non vérifié)
mar, 07/27/2021 - 16:39
Permalien
Exo 6
Bb fat (non vérifié)
lun, 04/04/2022 - 22:20
Permalien
Exellente résulta
Anonyme (non vérifié)
dim, 06/12/2022 - 16:17
Permalien
le reste
Ajouter un commentaire