Corrigé devoir n° 3 maths - 5e

Classe: 
Cinquième
 

Exercice 1

1) Recopions la (ou les) bonne(s) réponse(s) en justifiant brièvement.
 
(1) $\dfrac{7}{9}=\dfrac{7\times 2}{9\times 2}=\dfrac{7\div 2}{9\div 2}$
 
Le résultat d'une fraction ne change pas lorsqu'on divise ou on multiplie le numérateur et le dénominateur par un même nombre.
 
(2) $\dfrac{25}{35}\simeq 0.7=\dfrac{5}{7}$
 
Par calcul direct et en rendant irréductible.
 
(3) $\dfrac{28}{72}=\dfrac{7}{18}$
 
Par simplification.
 
2) Pour chaque expression, donnons la fraction égale irréductible (la plus simple possible)
 
On a :
 
$\begin{array}{rcl} A&=&\dfrac{72}{108}\\\\&=&\dfrac{2\times 36}{3\times 36}\\\\&=&\dfrac{2}{3}\end{array}$
 
Donc, $\boxed{A=\dfrac{2}{3}}$
 
$\begin{array}{rcl} B&=&\dfrac{32}{24}\\\\&=&\dfrac{4\times 8}{3\times 8}\\\\&=&\dfrac{4}{3}\end{array}$
 
D'où, $\boxed{B=\dfrac{4}{3}}$
 
$\begin{array}{rcl} C&=&0.4\\\\&=&\dfrac{4}{10}\\\\&=&\dfrac{2\times 2}{5\times 2}\\\\&=&\dfrac{2}{5}\end{array}$
 
Ainsi, $\boxed{C=\dfrac{2}{5}}$
 
3) Rendons irréductible les fractions ci-dessous en utilisant le $PGCD$
 
En décomposant $360\ $ et $\ 200$ en produits de facteurs premiers, on obtient :
 
$360=2^{3}\times 3^{2}\times 5\ $ et $\ 200=2^{3}\times 5^{2}$
 
Ainsi,
 
$\begin{array}{rcl} PGCD(360\;;\ 200)&=&2^{3}\times 5\\\\&=&40\end{array}$
 
Par suite,
 
$\begin{array}{rcl} \dfrac{360}{200}&=&\dfrac{360\div 40}{200\div 40}\\\\&=&\dfrac{9}{5}\end{array}$
 
D'où, $\boxed{\dfrac{360}{200}=\dfrac{9}{5}}$
 
De la même manière, en décomposant $450\ $ et $\ 72$ en produits de facteurs premiers, on obtient :
 
$450=2\times 3^{2}\times 5^{2}\ $ et $\ 72=2^{3}\times 3^{2}$
 
Donc,
 
$\begin{array}{rcl} PGCD(450\;;\ 72)&=&2\times 3^{2}\\\\&=&18\end{array}$
 
Par suite,
 
$\begin{array}{rcl} \dfrac{450}{72}&=&\dfrac{450\div 18}{72\div 18}\\\\&=&\dfrac{25}{4}\end{array}$
 
Ainsi, $\boxed{\dfrac{450}{72}=\dfrac{25}{4}}$
 
4) a) Montrons que $1\,029$ est un multiple de $147.$
 
On a : $1\,029=147\times 7$ donc, $1\,029$ est divisible par $147.$
 
D'où, $1\,029$ est un multiple de $147.$
 
b) Calculons $PGCD(1\,029\;;\ 147)\ $ et $\ PPCM(1\,029\;;\ 147).$
 
On a : $147=3\times 7^{2}\ $ et $\ 1\,029=3\times 7^{3}$
 
Alors,
 
$\begin{array}{rcl} PGCD(1\,029\;;\ 147)&=&3\times 7^{2}\\\\&=&147\end{array}$
 
Donc, $\boxed{PGCD(1\,029\;;\ 147)=147}$
 
$\begin{array}{rcl} PPCM(1\,029\;;\ 147)&=&3\times 7^{3}\\\\&=&1\,029\end{array}$
 
Ainsi, $\boxed{PPCM(1\,029\;;\ 147)=1\,029}$
 
On remarque que $1\,029\ $ et $\ 147$ sont respectivement le $PPCM\ $ et le $PGCD$ de $1\,029\ $ et $\ 147$

Exercice 2

a) Comparons en remplaçant les pointillés par : $<\ $ ou $\ >.$
 
$\dfrac{6}{7}>\dfrac{6}{13}\qquad\dfrac{14}{19}<\dfrac{14}{9}\qquad\dfrac{11}{3.5}>\dfrac{11}{3.11}$
 
b) Comparons en remplaçant les pointillés par : $<\ $ ou $\ >.$
 
$\dfrac{35}{7}>1\qquad\dfrac{7}{35}<1\qquad\dfrac{19}{29}<1$

Exercice 3

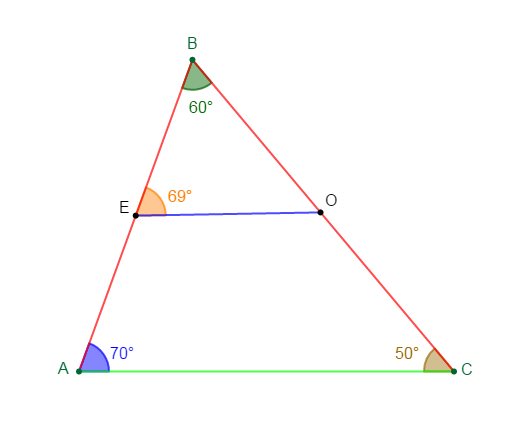
$ABC$ est un triangle tel que :
$$AC=7.5\;cm\;;\ \widehat{A}=70 ^{\circ}\ \text{ et }\ \widehat{C}=50^{\circ}$$
1) Construisons le triangle $ABC$
 
2) Calculons la mesure de l'angle $\widehat{B}$
 
On sait que dans un triangle, la somme des angles est égale à $180^{\circ}.$
 
Donc,
$$\widehat{B}+\widehat{A}+\widehat{C}=180^{\circ}$$
Par suite,
 
$\begin{array}{rcl} \widehat{B}&=&180^{\circ}-(\widehat{A}+\widehat{C})\\\\&=&180^{\circ}-(70^{\circ}+50^{\circ})\\\\&=&180^{\circ}-120^{\circ}\\\\&=&60^{\circ}\end{array}$
 
D'où, $\boxed{\widehat{B}=60^{\circ}}$
 
3) Construisons le point $E$ milieu de $[AB]$
 
4) Construisons le point $O\in(BC)$ tel que $\widehat{BEO}=69^{\circ}$
 
5) Les angles $\widehat{BAC}\ $ et $\ \widehat{BEO}$ sont correspondants.
 
6) Les droites $(EO)\ $ et $\ (AC)$ ne sont pas parallèles.
 
Justifions la réponse.
 
En effet, es angles $\widehat{BAC}\ $ et $\ \widehat{BEO}$ sont correspondants mais n'ont pas la même mesure.
 
Par conséquent, les droites $(EO)\ $ et $\ (AC)$ ne sont pas parallèles.
 

 

Auteur: 
Diny Faye

Commentaires

Laity Ndiaye Mbodji (non vérifié)

mar, 11/23/2021 - 13:48

Bonh je vous dit félicitations pour cette application elle est genial et sa aide beaucoup de personnes,comme elle m'aide moi

Eva ndiaye (non vérifié)

ven, 01/27/2023 - 21:24

Je dis félicitations cette application aide beaucoup de monde comme moi

Kouta (non vérifié)

lun, 04/10/2023 - 19:42

Avec les devoirs

wali (non vérifié)

mar, 01/23/2024 - 15:26

merci meilleur cite du monde entier

wali (non vérifié)

mar, 01/23/2024 - 15:28

merci pour tous

N.diéye (non vérifié)

jeu, 11/21/2024 - 22:12

Merci beaucoup

Ajouter un commentaire