Bac Physique chimie 1er groupe S1 S3 2019
Exercice 1 (03 points)
Il intervient également dans la préparation de fibres synthétiques.
Une masse de $146\;g$ de diméthylformamide contient $28\;g$ d'azote.
1.1. Montrer que la formule brute du diméthylformamide est $C_{3}H_{7}ON.$ (0.25 point)
1.2. Écrire les formules semi-développées possibles des amides compatibles avec cette formule brute et donner leurs noms. (01 point)
1.3 Sachant que le diméthylformamide possède deux groupes méthyles liés à un même atome, identifier cet amide en précisant sa formule semi-développée et son nom dans la nomenclature officielle. (0.25 point)
1.4. Pour synthétiser cet amide, on dispose des produits suivants :
chlorure de thionyle $(SOCl_{2})$, oxyde de phosphore $(P_{4}O_{10})$ , acide méthanoïque, acide éthanoïque, acide propanoïque, ammoniac, méthylamine, éthylamine et diméthylamine.
1.4.1. Proposer deux méthodes de synthèse rapides et totales du diméthylformamide.
Préciser pour chaque méthode les étapes et les produits utilisés. (0.75 point)
1.4.2. Écrire les équation-bilans des réactions correspondant à chaque méthode. (0.75 point)
On donne les masses molaires en $g\cdot mol^{-1}$ : $M(C)=12$ ; $M(O)=16$ ; $M(N)=14$ ; $M(H)=1$
Exercice 2 (03 points)
Pour cela, on introduit dans un bécher placé dans un bain d'eau glacée, $20\;mL$ de l'ester de densité $d=0.88$ et $80\;mL$ d'une solution d'hydroxyde de sodium de concentration $2.5\;mol\cdot L^{-1}.$
A partir du mélange obtenu on remplit neuf $(9)$ tubes à essais contenant chacun $10\;mL$ du mélange.
2.1 Écrire l'équation de la réaction qui se produit dans chaque tube.
Rappeler le nom de cette réaction. (0.5 point)
2.2 Calculer la concentration molaire initiale de l'ester dans chaque tube. (0.5 point)
2.3 L'un des réactifs est en excès ; lequel ?
Justifier la réponse. (0.5 point)
2.4 Une méthode chimique appropriée a permis de suivre l'évolution de la concentration molaire de l'alcool formé au cours du temps.
Les résultats obtenus sont les suivants :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline \text{t(min)}&0&2&6&10&15&20&25&30&40\\ \hline \text{[alcool]}mol\cdot L^{-1}&0.00&0.25&0.65&0.93&1.15&1.34&1.45&1.48&1.52\\ \hline \end{array}$$
2.4.1 Tracer la courbe donnant la concentration de l'alcool en fonction du temps
Échelle : $1\;cm$ pour $2\;min$ ; $1\;cm$ pour $0.1\;mol\cdot L^{-1}$ (0.5 point)
2.4.2 Déterminer, en $mol\cdot L^{-1}\cdot min^{-1}$, la vitesse volumique de formation de l'alcool aux dates $t_{1}=10\;min$ et $t_{2}=20\;min.$
Interpréter l'évolution de cette vitesse. (0.5 point)
2.4.3 Montrer que la réaction est totale. (0.25 point)
2.4.4 Définir le temps de demi-réaction et déterminer sa valeur. (0.25 point)
On donne les masses molaires en $g\cdot mol^{-1}$ : $M(C)=12$ ; $M(O)=16$ ; $M(H)=1$
Exercice 3 (04 points)
Du haut d'une colline dont le versant a la forme d'un plan incliné faisant un angle $\alpha$ avec l'horizontale, ils lancent un projectile supposé ponctuel, de masse $m$, à partir d'un point $O$ avec une vitesse initiale $\overrightarrow{v}_{0}$ faisant un angle $\beta$ avec le plan incliné $(\beta>\alpha).$
L'origine des dates $t_{0}=0$ est prise au moment du lancer du projectile en $O.$
L'étude du mouvement est rapportée au repère d'espace $(OX\;,\ OY)$ muni des vecteurs unitaires $\vec{i}$ et $\vec{j}$ pris dans le plan vertical contenant $\overrightarrow{v}_{0}$ et la ligne de plus grande pente du plan incliné (figure 1).
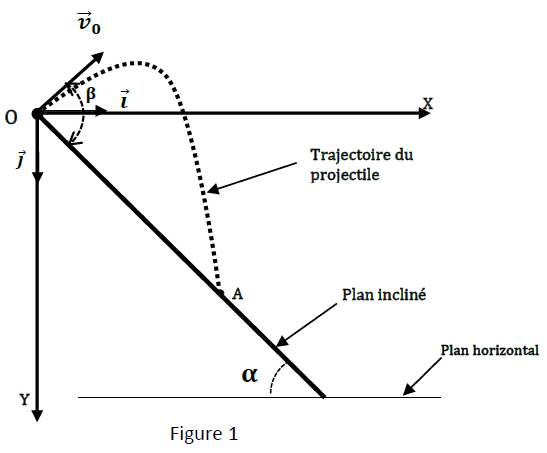
On néglige l'action de l'air sur le projectile.
3.1 Par application du théorème du centre d'inertie, établir les équations horaires $x(t)$ et $y(t)$ du mouvement du projectile. (0.5 point)
3.2 Établir l'expression de la date $t_{A}$ à laquelle le projectile tombe sur le plan incliné au point $A$ en fonction de $\alpha$, $\beta$, $\overrightarrow{v}_{0}$ et de l'intensité de la pesanteur $g.$ (0.5 point)
3.3 Montrer que la distance $d=OA$, appelée portée sur le plan incliné, peut se mettre sous la forme :
$$d=\dfrac{2v_{0}^{2}\sin\beta\cos(\beta-\alpha)}{g(\cos\alpha)^{2}}.\qquad(0.75\;point)$$
3.4 Le groupe d'élèves effectue des tirs avec des vitesses initiales de même valeur $v_{0}$.
3.4.1 Établir, en fonction de $\alpha$, l'expression de la valeur $\beta_{L}$ de l'angle $\beta$ pour laquelle la portée prend une valeur maximale $d_{max}.$ (0.75 point)
3.4.2 En déduire l'expression de cette portée $d_{max}$ en fonction de $g$, $\alpha$ et $v_{0}.$ (0.5 point)
3.5 On considère un lancer de vitesse initiale $v_{0}=12\;m\cdot s^{-1}$ avec $\alpha=60^{\circ}$
3.5.1 Calculer $\beta_{L}$ et $d_{max}$ (0.5 point)
3.5.2 Calculer Le temps mis par le projectile pour tomber sur le plan incliné pour $\beta=\beta_{L}.$ (0.5 point)
On prendra : $g=9.8\;m\cdot s^{-2}$
Exercice 4 (05 points)
En effet l'eau lourde est utilisée comme ralentisseur de neutrons dans les centrales nucléaires permettant ainsi d'obtenir des réactions en chaîne contrôlées L'isotope $_{92}^{235}U$ de l'uranium, qui se retrouve dans les minerais d'uranium en quantité très faible, est fissile.
L'une des réactions de fission s'écrit :
$$_{92}^{235}U+^{1}_{0}n\ \rightarrow\ _{x}^{139}Xe+^{y}_{38}Sr+2_{0}^{1}n$$
4.1 A partir des lois de conservation de la charge et de la matière, déterminer $x$ et $y.$ (0.5 point)
4.2 L'énergie libérée par la fission d'un noyau d'uranium $235$ est $200$ $MeV.$
4.2.1 Déterminer la variation de masse que subit le système en $kg$ et en $u$ (unité de masse atomique). (0.5 point)
4.2.2 Une centrale nucléaire consomme de l'uranium $235$ selon la réaction ci-dessus.
Elle fournit une puissance électrique de $3.4\;MW.$
Sachant que $40\%$ de l'énergie libérée lors de la fission est transformé en énergie électrique, calculer la masse d'uranium $235$ consommée par jour. (0.75 point)
4.3 Un neutron provenant de cette réaction de fission est expulsé avec une vitesse $\overrightarrow{V}_{0}$ de valeur (norme) $V_{0}=20000\;km\cdot s^{-1}.$
Pour contrôler cette réaction de fission, il faut ralentir les neutrons grâce à des chocs successifs sur d'autres noyaux initialement au repos $(V_{R}=0)$ jusqu'à obtenir au bout de $n$ chocs, une vitesse des neutrons $v_{n}=2.94\;km\cdot s^{-1}$ (figure 2).
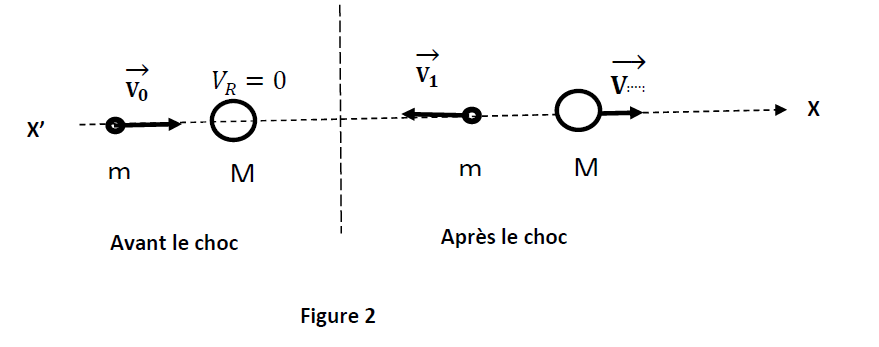
Les chocs sont supposés élastiques et les vitesses colinéaires (choc frontal).
On notera $m$ la masse du neutron et $M$ celle d'un noyau au repos heurté par le neutron.
4.3.1 Soient $\overrightarrow{V}_{1}$ la vitesse du neutron juste après le premier choc et $\overrightarrow{V}$ la vitesse du noyau-cible juste après le choc.
On considère le système formé par le neutron et le noyau cible.
a) Donner l'expression du vecteur quantité de mouvement du système avant le choc puis son expression après le choc. (0.25 point)
b) Donner l'expression de l'énergie cinétique du système avant le choc puis son expression après le choc. (0.25 point)
c) En appliquant la conservation de la quantité de mouvement et celle de l'énergie cinétique montrer qu'après le premier choc la valeur $V_{1}$ de la vitesse du neutron est donnée par :
$$V_{1}=\dfrac{(M-m)V_{0}}{M+m}\qquad(01\;point)$$
4.3.2 Déduire de la question précédente l'expression de la vitesse $V_{2}$ du neutron après le deuxième choc en fonction de $m$, $M$ et $V_{0}.$ (0.5 point)
4.3.3 Montrer qu'après $n$ chocs la vitesse du neutron peut s'écrire $v_{n}=v_{0}\cdot q^{n}$ ; on donnera l'expression de $q.$ (0.75 point)
4.3.4 Calculer le nombre $n$ de chocs nécessaire sur des noyaux de deutérium sachant que le rapport de la masse du deutérium sur la masse du neutron vaut $\dfrac{M}{m}=2.$ (0.5 point)
Données :
Célérité de la lumière dans le vide : $C=3\cdot10^{8} m\cdot s^{-1}$ ;
$1eV=1.6\cdot 10^{-19}J$ ;
$1\text{ jour}=86420\;s$ ;
Constante d'Avogadro : $N=6.02\cdot10^{23}mol^{-1}$ ;
$1u=\text{une unité de masse atomique}=1.6\cdot 10^{-27}kg.$
Exercice 5 (05 points)
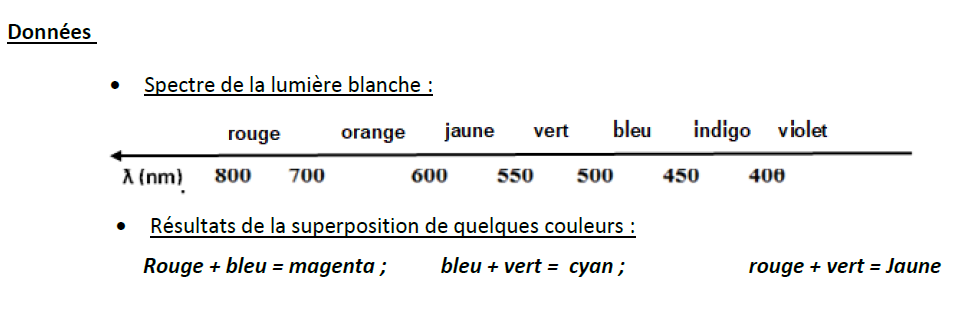
L'existence de certaines couleurs peut s'expliquer, entre autres, par la superposition de couleurs primaires.
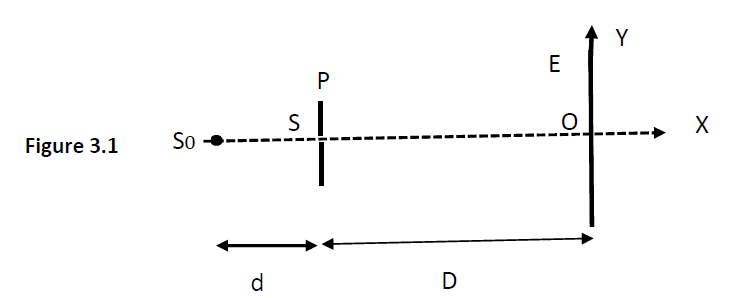
5.1 Une source lumineuse monochromatique $S_{0}$ émet une radiation de longueur d'onde $\lambda.$
Elle est placée à une distance $d$ d'un plan opaque $(P)$ percé d'un trou circulaire $S$ de diamètre $a<\lambda.$
Les rayons lumineux arrivent perpendiculairement au plan $(P)$ en traversant le trou.
Un écran $(E)$ est placé parallèlement au plan $(P)$, à une distance $D=2\;m$ (figure 3.1).
Quel phénomène physique se produit lorsque le faisceau de lumière traverse le trou circulaire ?
Justifier votre réponse. (0.25 point)
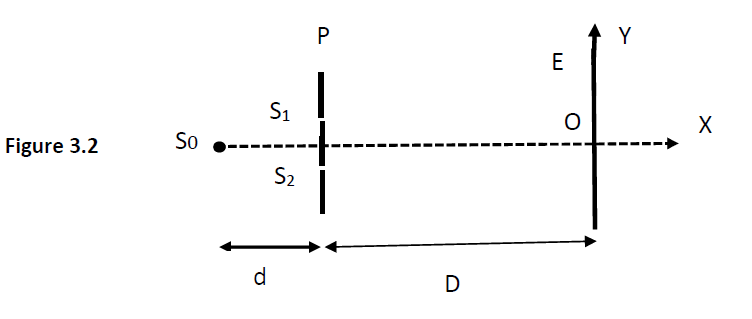
5.2 On reprend le dispositif décrit précédemment, le plan $(P)$ est percé maintenant de deux trous fins $(S_{1})$ et $(S_{2}).$
La source $S_{0}$ est placée à égale distance des trous et à une distance $d$ du plan opaque $(P).$
Les distances $d$ et $D$ sont maintenues (figure 3.2).
5.2.1 La radiation monochromatique utilisée a une fréquence $v=5.77\cdot 10^{14}Hz$
5.2.1.1 Quelle est la couleur de la lumière utilisée ? (le spectre de la lumière blanche figure dans les données fournies à la fin de l'exercice).
Célérité de la lumière dans le vide : $C=3\cdot10^{8}m/s$ (0.5 point)
5.2.1.2 Qu'observe-t-on sur l'écran $(E)$ ? (0.5 point)
5.2.1.3 Comment appelle-t-on ce phénomène ?
Quel caractère de la lumière est ainsi mis en évidence ? (0.75 point)
5.2.1.4 Le milieu de la cinquième $(5^{ième})$ frange brillante est situé à une ordonnée $y=2.6\;mm$ (l'origine $O$ est le point de rencontre entre l'axe de symétrie $(S_{0}x)$ et l'écran $(E)$).
L'ordre de La frange centrale est zéro $(0).$
a) Déterminer la distance $b$ séparant les deux sources secondaires $(S_{1})$ et $(S_{2}).$ (0.5 point)
b) Définir puis calculer l'interfrange $i.$ (0.5 point)
c) Quelle est la nature de la frange située à $y=1.3\;mm$ et celle située à $y=2.08\;mm$ ?
Justifier votre réponse. (0.5 point)
5.2.2 On remplace la source $S_{0}$ par une lampe spectrale émettant deux radiations $\lambda_{1}=750\;nm$ et $\lambda_{2}=480\;nm.$
5.2.2.1 Quelle est la couleur de la frange observée sur l'écran à $y=0$ ?
Justifie (0.5 point)
5.2.2.2 A quelle distance minimale $h$ de l'origine $O$ sur l'écran va-t-on observer à nouveau l'aspect décrit à la question 5.2.2.1 ? (01 point)

Commentaires
MouminyBah (non vérifié)
jeu, 11/14/2019 - 16:13
Permalien
Demande de sujet bac resolut
Bah Mohamadou M (non vérifié)
jeu, 03/18/2021 - 21:02
Permalien
Demande des sujet résolus.
Bah (non vérifié)
jeu, 03/18/2021 - 21:59
Permalien
Demande des sujets resolu
Djibi (non vérifié)
ven, 11/05/2021 - 01:27
Permalien
Demande de correction
Mamoudou Traoré (non vérifié)
sam, 06/10/2023 - 12:07
Permalien
Bac
Oumou Ba (non vérifié)
mer, 02/14/2024 - 12:50
Permalien
Correctiom
Moussa200 (non vérifié)
dim, 03/17/2024 - 15:42
Permalien
demande solution
Anonyme (non vérifié)
mar, 04/16/2024 - 21:10
Permalien
i want that
Cheikh fall (non vérifié)
mar, 11/26/2024 - 00:55
Permalien
Je vais la correction de l exercice 3
Thomas Passoule... (non vérifié)
lun, 03/03/2025 - 20:59
Permalien
Correction de l'exercice
Ajouter un commentaire