Corrigé devoir n° 4 maths - 5e
Classe:
Cinquième
Exercice 1
On donne les expressions suivantes :
$$D=\left(\dfrac{5}{2}-\dfrac{1}{6}\right)+\left(\dfrac{4}{3}+5\right)\qquad E=\dfrac{2}{5}\times\dfrac{4}{3}\times 6$$
$$F=\dfrac{7}{3}+\dfrac{2}{9}-4\qquad G=\dfrac{10}{3}+\dfrac{5}{2}\div 3$$
$$F=\dfrac{7}{3}+\dfrac{2}{9}-4\qquad G=\dfrac{10}{3}+\dfrac{5}{2}\div 3$$
1) Calculons chacune des expressions $D\;;\ E\;;\ F\ $ et $\ G$ puis simplifions les résultats.
$\begin{array}{rcl} D&=&\left(\dfrac{5}{2}-\dfrac{1}{6}\right)+\left(\dfrac{4}{3}+5\right)\\\\&=&\left(\dfrac{15}{6}-\dfrac{1}{6}\right)+\left(\dfrac{4}{3}+\dfrac{15}{3}\right)\\\\&=&\left(\dfrac{15-1}{6}\right)+\left(\dfrac{4+15}{3}\right)\\\\&=&\dfrac{14}{6}+\dfrac{19}{3}\\\\&=&\dfrac{2\times 7}{2\times 3}+\dfrac{19}{3}\\\\&=&\dfrac{7}{3}+\dfrac{19}{3}\\\\&=&\dfrac{26}{3}\end{array}$
Donc, $\boxed{D=\dfrac{26}{3}}$
$\begin{array}{rcl} E&=&\dfrac{2}{5}\times\dfrac{4}{3}\times 6\\\\&=&\dfrac{2\times 4\times 6}{5\times 3}\\\\&=&\dfrac{48}{15}\\\\&=&\dfrac{3\times 16}{3\times 5}\\\\&=&\dfrac{16}{5}\end{array}$
Ainsi, $\boxed{E=\dfrac{16}{5}}$
$\begin{array}{rcl} F&=&\dfrac{7}{3}+\dfrac{2}{9}-4\\\\&=&\dfrac{21}{9}+\dfrac{2}{9}-\dfrac{36}{9}\\\\&=&\dfrac{21+2-36}{9}\\\\&=&-\dfrac{13}{9}\end{array}$
D'où, $\boxed{F=-\dfrac{13}{9}}$
$\begin{array}{rcl} G&=&\dfrac{10}{3}+\dfrac{5}{2}\div 3\\\\&=&\dfrac{10}{3}+\dfrac{5}{2}\times\dfrac{1}{3}\\\\&=&\dfrac{10}{3}+\dfrac{5}{6}\\\\&=&\dfrac{20}{6}+\dfrac{5}{6}\\\\&=&\dfrac{25}{6}\end{array}$
Donc, $\boxed{G=\dfrac{25}{6}}$
2) a) Mettons ces résultats sous la forme de $q+\dfrac{r}{b}$
On a : $D=\dfrac{26}{3}$
Donc, on peut écrire :
$\begin{array}{rcl} D&=&\dfrac{24+2}{3}\\\\&=&\dfrac{24}{3}+\dfrac{2}{3}\\\\&=&8+\dfrac{2}{3}\end{array}$
Ainsi, $\boxed{D=8+\dfrac{2}{3}}$
Soit : $E=\dfrac{16}{5}$
Alors, on peut écrire :
$\begin{array}{rcl} E&=&\dfrac{15+1}{5}\\\\&=&\dfrac{15}{5}+\dfrac{1}{5}\\\\&=&3+\dfrac{1}{5}\end{array}$
D'où, $\boxed{E=3+\dfrac{1}{5}}$
On a : $F=-\dfrac{13}{9}$
Donc, on peut écrire :
$\begin{array}{rcl} F&=&\dfrac{-18+5}{9}\\\\&=&\dfrac{-18}{9}+\dfrac{5}{9}\\\\&=&-2+\dfrac{5}{9}\end{array}$
Par suite, $\boxed{F=-2+\dfrac{5}{9}}$
Soit : $G=\dfrac{25}{6}$
Alors, on peut écrire :
$\begin{array}{rcl} G&=&\dfrac{24+1}{6}\\\\&=&\dfrac{24}{6}+\dfrac{1}{6}\\\\&=&4+\dfrac{1}{6}\end{array}$
D'où, $\boxed{G=4+\dfrac{1}{6}}$
b) Rangeons ces résultats dans l'ordre croissant.
On sait que :
$$\left(-2+\dfrac{5}{9}\right)<\left(3+\dfrac{1}{5}\right)<\left(4+\dfrac{1}{6}\right)<\left(8+\dfrac{2}{3}\right)$$
Donc, dans l'ordre croissant, on a :
$$F\;;\ E\;;\ G\;;\ D$$
3) Donnons un encadrement de $D$ à l'unité prés
On sait que : $0<\dfrac{2}{3}<1$
Donc, en ajoutant $8$ à chaque de l'inégalité, on obtient :
$8+0<8+\dfrac{2}{3}<8+1$
Par suite, $8<\left(8+\dfrac{2}{3}\right)<9$
D'où, un encadrement de $D$ à l'unité prés est donné par :
$$8<D<9$$
Exercice 2
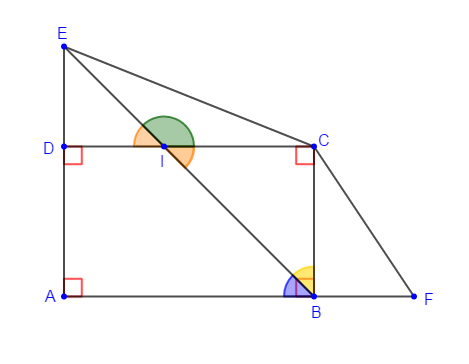
En nous aidant de la figure ci-dessous, donnons le nom de $2$ angles :
1) adjacents et complémentaires
$\widehat{ABI}\ $ et $\ \widehat{CBI}$ sont deux angles adjacents et complémentaires.
2) adjacents et supplémentaires
$\widehat{DIE}\ $ et $\ \widehat{EIC}$ sont deux angles adjacents et supplémentaires.
3) opposés par le sommet
$\widehat{CIB}\ $ et $\ \widehat{DIE}$ sont deux angles opposés par le sommet.
Exercice 3
Sur la figure ci-dessous, le triangle $EFG$ est isocèle en $E.$
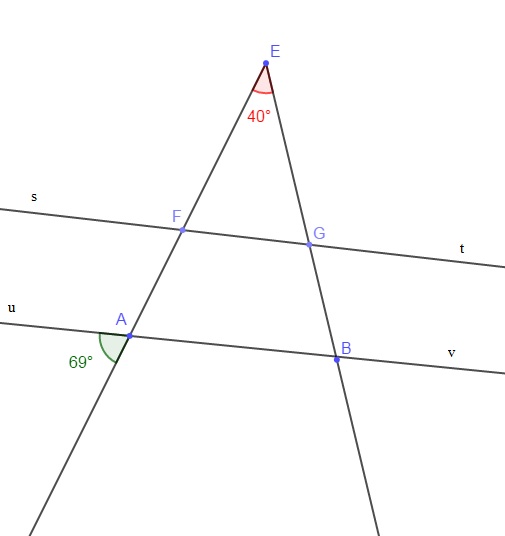
Les droites $(FG)\ $ et $\ (AB)$ ne sont pas parallèles
Justifions la réponse par des calculs d'angles
En effet, le triangle $EFG$ étant isocèle en $E$ alors, $\widehat{EFG}=\widehat{EGF}.$
Or, dans un triangle la somme des angles est égale à $180^{\circ}.$
Donc, $\widehat{EFG}+\widehat{EGF}+\widehat{GEF}=180^{\circ}$
Ainsi, $\widehat{EFG}+\widehat{EGF}=180^{\circ}-40^{\circ}=140^{\circ}.$
Comme $\widehat{EFG}=\widehat{EGF}$ alors, $\widehat{EFG}+\widehat{EGF}=2\widehat{EFG}$
Par suite, $2\widehat{EFG}=140^{\circ}.$
D'où, $\widehat{EFG}=\dfrac{140^{\circ}}{2}=70^{\circ}.$
On constate alors que l'angle $\widehat{A}$ et l'angle $\widehat{EFG}$ n'ont pas la même mesure.
Or, ces deux angles sont alternes-externes.
Par conséquent, les droites $(FG)\ $ et $\ (AB)$ ne sont pas parallèles.
Auteur:
Diny Faye

Commentaires
Ibrahima Mbengue (non vérifié)
dim, 01/14/2024 - 20:08
Permalien
Faire des cours de renforcement
Moustapha diaw (non vérifié)
jeu, 04/25/2024 - 21:15
Permalien
Maths
Ajouter un commentaire